5.1 INTRODUCTION

In the last decade, agent-based modeling and simulation (ABMS) has been successfully applied to a variety of domains, demonstrating the potential of this technique to advance science, engineering, and policy analysis (North and Macal, 2007). However, realizing the full potential of ABMS to find breakthrough results in research areas such as social science and microbial biodiversity will surely require far greater computing capability than is available through current ABMS tools. The Repast for High Performance Computing (Repast HPC) project hopes to realize this potential by developing a next-generation ABMS system explicitly focusing on large-scale distributed computing platforms.

This chapter’s contribution is its detailed presentation of the implementation of Repast HPC as a useful and usable framework. Section 5.2 discusses agent simulation in general, providing a context for the more detailed discussion of Repast HPC that follows. Section 5.3 describes the motivation for our work and the limits of current attempts to increase the computational capacity of ABMS toolkits. Section 5.4 discusses the salient aspects of our existing Repast HPC toolkit that guide the development of Repast HPC. In Section 5.5, we explore the parallelization of an ABMS in a more general way, and Section 5.6 describes the current implementation. Section 5.7 introduces an example Repast HPC social science “rumor” application, while Section 5.8 presents a concluding discussion.

5.2 AGENT SIMULATION

ABMS is a method of computing the potential system-level consequences of the behaviors of sets of individuals (North and Macal, 2007). ABMS allows modelers to specify each agent’s individual behavioral rules, to describe the circumstances in which the individuals reside, and then to execute the rules to determine possible system results. Agents themselves are individually identifiable components that usually represent decision makers at some level. Agents are often capable of some level of learning or adaptation ranging from a simple parameter adjustment to the use of neural networks or genetic algorithms. For more information on ABMS, see North and Macal (2007).

5.3 MOTIVATION AND RELATED WORK

The growing roster of successful ABMS applications demonstrates the enormous potential of this technique. However, current implementations of ABMS tools do not currently focus on very rich models or high-performance computing platforms. Many recent efforts to increase the computational capacity of ABMS toolkits have focused on either simple parameter sweeps or the use of standardized but performance-limited technologies. In contrast, Repast HPC’s focus is on enabling distributed runs over multiple processes. In doing so, Repast HPC enables (1) massive individual runs, that is, runs containing a number of agents sufficient to overwhelm a single process; and (2) runs containing relatively few complex agents where the computational complexity would overwhelm a single process. ABMS studies typically require the execution of many model runs to account for stochastic variation in model outputs as well as to explore the possible range of outcomes. These ensembles of runs are often organized into “embarrassingly parallel” parameter sweeps due to the way that the independence of the individual model runs allows them to be easily distributed over large numbers of processors on high-performance computers. Quite a few groups have developed tools such as Drone¹ and OMD (Koehler and Tivnan, 2005) for performing such parameter sweeps on high-performance computing systems. Unfortunately, many of the most interesting agent-based modeling problems, such as microbial biodiversity, the social-aspects of climate change, and others yet to be developed, require extremely large individual model runs rather than large numbers of smaller model runs. The parameter sweep approach does not offer a solution to this need.

The need for extremely large individual model runs has led various research groups to employ existing standards such as high-level architecture (HLA)² and various kinds of Web services (Houari and Far, 2005). These widely used standards can be effective for their purposes, but they are not designed to work efficiently on extremely large computing platforms. This ultimately limits their ability to address the need for extremely large individual model runs. Unfortunately, attempts to introduce new distributed ABMS standards, such as the Foundation for Intelligent Physical Agents (FIPA) architecture specifications³ and KAoS (Bradshaw, 1996), have succumbed to the same problem. However, despite difficulties in efforts to leverage existing standards as well as the more common focus on large numbers of relatively small model runs, a few groups have developed tools and frameworks for distributing large numbers of agents in a single model across a large number of processors. Deissenberg, van der Hoog, and Dawid’s EURACE project (Deissenberg and Hoog, 2009) attempts to construct an agent-based model of the European economy with a very large (up to approximately 10⁷) population of agents. Agent-based computational economics (ACE) is a fertile area of research, and while it is important to note that the map (i.e., the model) is not (and need not be) territory, larger models are needed in order to explore the complexity and scope of an actual economy.

EURACE will be implemented using the Flexible Large-Scale Agent Modeling Environment (FLAME). FLAME’s origins are in the large-scale simulation of biological cell growth. Each agent is modeled as a “Stream X-Machine” (Laycock, 1993). A Stream X-Machine is a finite state machine consisting of a set of finite states, transition functions, and input and output messages. The state of a Stream X-Machine is determined by its internal memory. For example, the memory may contain variables such as an ID, and x and y positions (Deissenberg and Hoog, 2009). Agents communicate by means of messages, and their internal state is modified over time by transition functions that themselves may incorporate input messages and produce output messages. This representation of agents as Stream X-Machines is similar to Repast’s representation of agents as objects, the internal state of which is captured by fields, and the behavior of which is modeled by methods (see next discussion). It is unclear, though, how EURACE/FLAME implements topological (network, spatial, etc.) relations between agents other than via internal memory variables. In contrast, Repast uses more flexible contexts and projections (see next discussion).

In common with other large-scale agent simulation platforms, including Repast, EURACE leverages the fact that much agent communication is local. By clustering “neighboring” agents on the same process, costly interprocess communication can be reduced. Here “neighbor” refers to agents within each others’ sphere of influence. Thus, an agent may be a network neighbor of an agent whose simulated spatial location is much further away. Of course, there are complications with this approach in that it may not always be possible to arrange agents in a process-compatible way. For example, an agent may need to participate in a network whose other members’ simulated spatial location is not architecturally local to that agent. Nevertheless, this principle of distributing agents across processes according to neighborhood or sphere of influence is often efficient and is common to agent simulation platforms.

The SimWorld Agent-Based Grid Experimentation System (SWAGES) (Scheutz et al., 2006) platform provides automatic parallelization via its SimWorld component. The automatic parallelization algorithm uses spatial information from the simulation to calculate agents’ spheres of influence and to distribute the agents across processes accordingly. However, such automatic parallelization as described in Scheutz et al. (2006) works only with explicitly spatial simulations rather than with other agent environment topologies.

SWAGES itself is composed of both client and server components and runs on both fixed and dynamic clusters of machines. Most of the server components, running on a single host, manage various aspects of the distributed simulation infrastructure, while the component that manages clients most directly represents the remote simulation and stores the shared simulation state. SWAGES provides an integrated platform for distributed agent-based simulation including data collection and so forth, but unlike Repast HPC, SWAGES is not designed to run on massively parallel machines such as IBM’s Blue Gene. Agent implementation must be done in the Poplog programming languages (i.e., Pop11, Prolog, ML, Scheme, C-Lisp) rather than in more common languages such as C++ (used by Repast HPC). Kwok and Chow (2002), although not working in a strictly parallel context, emphasize the importance of proximity and “sphere of influence” with respect to load balancing. Their concern is load balancing for distributed multiagent computing. Agents in this case are more or less autonomous actors performing some task on behalf of an end user. For example, agents may be deployed to locate the lowest price of some commodity in a financial market. In this case, the agents can be thought of as “brokers” and the interaction between them as an exchange of “services.” Their Comet load balancing algorithm uses a “credit”-based model for managing the distribution of agents among a cluster of machines. Each agent is dynamically assigned a credit score based on a variety of factors, among which are the computational workload and the proximity of the agents with which the scored agent communicates. The idea is that moving agents off of a process that contains the agents with which it communicates will adversely affect the efficiency of the system. Although the algorithmic work of Kwok and Chow (2002) provides avenues of investigation for Repast HPC’s load balancing, it differs significantly. It is not concerned with very large numbers of agents, and its notion of agents and an agent simulation environment obviously differs.

In a more strictly parallel context, Oguara et al. (2006) also utilize the sphere of influence notion, describing an adaptive load management mechanism for managing shared state, the goal of which is to minimize the cost of accessing the shared state while balancing the cost of managing, migrating, and so on, of the shared state. The cost is minimized by decomposing the shared state according to a sphere of influence and by distributing it so that the shared state is as local as possible to the agents that access it most frequently. The benefits of this minimization are balanced relative to the computational load of actually accomplishing it. Oguara et al. (2006) explore the mechanism using the parallel discrete-event simulation–multiagent system (PDES-MAS) framework. PDES-MAS represents agents as an agent logical process. Agent logical processes have both private internal state and public shared state. The shared state is modeled as a set of variables. Any operation on the shared state (i.e., reading or writing) is a time-stamped event. The sphere of influence of an event is the set of shared state variables accessed by that event. Given the time stamp, the frequency of shared state access can be calculated.

PDES-MAS also contains communication logical processes that manage the shared state. Communication logical processes are organized as a tree whose branches terminate in the agent logical processes. The shared state is distributed and redistributed among the communication logical process tree nodes as the shared state variable migration algorithm is run. When an agent accesses the shared state, that request is routed through the tree and is processed by the communication logical process nodes. The history of this access is recorded and the shared state migration algorithm evaluates the cost of access in order to determine when and how the shared state should be migrated. Additional work is done to avoid bottlenecks (i.e., concentrating too much shared state in too few communication logical processes) as well as to balance the computational cost of migration.

As compelling as the contribution of Oguara et al. (2006) is, it does not provide a full agent simulation package, lacking such things as topology (grid, network, etc.) management, data collection, and so on, that Repast HPC contains. We would in the future like to leverage their work on the efficient management of shared state. The object-oriented nature of Repast HPC’s agents makes such externalization of shared state much easier than it might otherwise be. Furthermore, much shared state is the agents’ environment as represented by topologies such as grids and networks. Repast HPC externalizes these topologies in separate projection objects, making their management in a distributed context much easier.

Massaioli et al. (2005) take a different approach to the problems of shared state. After experimenting with Message Passing Interface (MPI)-based agent simulations and deciding that the overhead of communicating and synchronizing shared state was too high, Massaioli and his colleagues explore a shared-memory OpenMP-based approach. The majority of their paper (Massaioli et al., 2005) then evaluates the efficiency of various OpenMP idioms in parallelizing typical agent-based simulation structures. In particular, they address optimizing the iteration and evaluation of non-fixed-length structures such as linked lists of pointers. OpenMP is very good at processing the elements of fixed-length arrays in parallel, and Massaioli et al. (2005) investigate how to achieve a similar performance over linked lists of pointers. Although they do highlight issues of sharing and synchronizing states via MPI, we believe a properly architected platform (of which Repast HPC is the first step) can avoid or at least minimize these issues. Indeed, the work of Oguara et al. (2006) illustrates how this might be done. Furthermore, an OpenMP-based approach assumes a shared-memory architecture that may be present within a processor node, but not necessarily across all the nodes. Other works, although not strictly focusing on the large-scale execution of ABMS applications, explore the related area of parallel discrete-event simulation (PDES) (Fujimoto, 1990, 2000). Such work typically focuses on parallel event synchronization where logical processes communicate and synchronize with each other through time-stamped events. Three approaches are commonly used: conservative, optimistic, and mixed mode (Perumulla, 2006, 2007). The conservative approach blocks the execution of the process, ensuring the correct ordering of simulation events (Chandy and Misra, 1979, 1981). The optimistic approach avoids blocking but must compensate when events have been processed in the incorrect order. The Time Warp operating system is the preeminent example of this approach (Jefferson, 1985; Jefferson et al., 1987). Mixed mode combines the previous two (see, e.g., Perumulla [2005] and Jha and Bagrodia [1994]). The trio of Sharks World papers (Nicol and Riffe, 1990; Presley et al., 1990) explores the application of these approaches to the Sharks World simulation (sharks eating and fish swimming in a toroidal world). The scalability of these approaches to more recent high-performance computing platforms such as IBM’s Blue Gene is discussed by Perumulla (2007), where he demonstrates scalability to over 10,000 CPUs.

Perumalla’s microkernel for parallel and distributed simulation, known as “μsik” (Perumulla, 2005, 2007) provides efficient PDES time scheduling. The correctness of simulation results requires that events are executed such that “global time-stamp order” execution is preserved. In essence, no process should execute events with time stamps less than its current time stamp, at least without compensation as in the optimistic approach described earlier. Doing this efficiently requires that global parallel synchronization must be fast.

The μsik microkernel (Perumulla, 2005, 2007) optimizes execution efficiency by minimizing the costs of rollback support, using a fast scalable algorithm for global virtual time (GVT) computation, and by minimizing the cost of fossil (i.e., unnecessary state and event history) collection. By memory reduction techniques such as employing reverse computation for rollback rather than state saving, significant improvements were achieved. Perumulla (2007) also illustrates how key algorithms, such as the GVT computation, scale effectively to 10⁴ processors without significant inefficiencies. Memory reduction is also helped by μsik’s fast logarithmic fossil collection. With respect to event scheduling, Repast HPC uses a distributed discrete-event scheduler that is, at least in the current implementation, tightly synchronized across processes. In this, it has more in common with conservative PDES synchronization algorithms as discussed earlier (Chandy and Misra, 1979, 1981). Peramulla (2005, 2007) illustrates well the complexities and concomitant performance payoffs associated with more sophisticated scheduling. The initial implementation of the Repast HPC scheduler avoids such complexities but leaves room for implementing more advanced parallel scheduling algorithms in the future. Lastly, although μsik does provide sophisticated PDES support, unlike Repast HPC, it does not provide the additional services needed for agent modeling such as topology management, data logging, and so forth.

Like Perumalla (2005, 2007), Bauer et al. (2009) implement and test efficient discrete time scheduling. In particular, they demonstrate scalable performance of a Time Warp-based simulator using reverse computation for rollback. Their results show effective scaling up to 32,768 processors on an IBM Blue Gene/L and up to 65,536 processors on a Blue Gene/P. They attribute the ability to scale to their message/network management algorithms that are tuned to leverage Blue Gene’s high-performance asynchronous message capabilities. Their implementation is based on ROSS: Rensselear’s Optimistic Simulation System (Carothers et al., 2002).

As in the case of Perumalla, Bauer et al. (2009) focus on PDES optimization and experimentation and unlike our work, they do not support the additional services needed for agent modeling such as topology management, data logging, and so forth. In addition, while they leverage Blue Gene’s message capabilities to achieve their efficiencies, Repast HPC aims at more general applicability. Notwithstanding these considerations, we hope to benefit from their work in the future in implementing more sophisticated parallel scheduling algorithms.

Karimabadi et al. (2006) study PDES for selected classes of grid models, in particular, hybrid models of electromagnetism. Their basic strategy is to use an approach similar to lazy program evaluation (Hudak, 1989). In other words, they set up their PDES to only execute an event when the consequences of that event are needed by some other event. Implementing their algorithm using Perumalla’s μsik (Perumulla, 2005) engine, they report a greater than 100-fold performance improvement over traditional PDES. Unfortunately, their algorithm is limited in the kinds of events it can support. Furthermore, like Perumalla’s μsik (Perumulla, 2005), they do not provide the additional services needed for agent modeling.

Some researchers such as D’Souza and colleagues (D’Souza et al., 2007; Lysenko and D’Souza, 2008) have studied the use of graphical processing units (GPUs) either individually or in large groups. In general, substantial speedups are found, but at the expense of a substantial reduction in modeling flexibility. GPUs are designed to rapidly and repeatedly execute small sets of instructions using limited instruction sets. This allows the underlying GPU hardware to be highly optimized for both speed and production cost. Efficient use of GPUs implies that the executing agents will tend to run the fastest when they have simple behaviors drawn from a short shared list of options.

This chapter’s contribution is its detailed presentation of the implementation of Repast HPC, the first complete ABMS platform developed explicitly for large-scale distributed computing systems. Our work on Repast HPC provides an integrated ABMS toolkit targeted at massive individual runs on high-performance computing platforms. In this, it differs from tools that enable distributed parameter sweeps over many individual runs. We leverage the related work done in distributed ABMS and PDES and hope to take more advantage of it in the future, but our focus is on a working integrated toolkit that provides the typical ABMS components specialized for a massively parallel environment. In addition, using standards such as MPI and C++, the code itself is compatible across multiple computing platforms.

Related work and how it compares to this chapter and Repast HPC is summarized next.

Belding (Drone)

• Citation: Koehler and Tivnan (2005)
• Summary: distributed parameter sweeps of relatively small runs
• How Repast HPC Differs: support for very large individual model runs

IEEE, FIPA

• Citation: Houari and Far (2005) and Bradshaw (1996)
• Summary: standards for model interoperability and distribution
• How Repast HPC Differs: actual working system for very large-sized model runs

EURACE

• Citation: Deissenberg and Hoog (2009)
• Summary: extremely large-scale distributed model of European economy
• How Repast HPC Differs: flexible and generic components based on contexts and projections

FLAME

• Citation: http://www.flame.ac.uk
• Summary: flexible large-scale agent modeling architecture based on Stream X-Machines
• How Repast HPC Differs: flexible and generic components based on contexts and projections using standard OO-techniques

SWAGES

• Citation: Scheutz et al. (2006)
• Summary: distributed simulation systems for large-scale ABMS
• How Repast HPC Differs: supports parallelization of more than just spatial simulations

Load Balancing

• Citation: Kwok and Chow (2002)
• Summary: load balancing for distributed multiagent computing
• How Repast HPC Differs: supports very large-sized distribution and employs a different although related notion of an agent

PDES-MAS

• Citation: Oguara et al. (2006)
• Summary: explores adaptive load management for managing shared state
• How Repast HPC Differs: less sophisticated shared state management but working support for all the typical agent simulation components

OpenMP for Agent-Based Simulation

• Citation: Massaioli et al. (2005)
• Summary: explores and evaluates the use of OpenMP in parallelizing agent-based simulation structures
• How Repast HPC Differs: uses MPI and provides a full set of working ABMS components.

PDES Scheduling in Sharks World

• Citation: Bagrodia and Liao (1990), Presley et al. (1990), and Nicol and Riffe (1990)
• Summary: explore PDES scheduling (conservative, optimistic, and mixed mode) in the context of the Sharks World simulation
• How Repast HPC Differs: simpler scheduling but working support for all the typical agent simulation components

μsik PDES Kernel

• Citation: Perumulla (2005)
• Summary: describes how the μsik PDES kernel provides efficient event scheduling
• How Repast HPC Differs: simpler scheduling but working support for all the typical agent simulation components

μsik Scalability

• Citation: Perumulla (2007)
• Summary: describes how μsik scales to very large sizes
• How Repast HPC Differs: simpler scheduling but working support for all the typical agent simulation components on high-performance computing machines.

Lazy PDES Event Execution

• Citation: Karimabadi et al. (2006)
• Summary: explores the use of lazy PDES event execution using the μsik kernel
• How Repast HPC Differs: simpler scheduling but working support for all the typical agent simulation components

GPUs for ABMS

• Citation: D’Souza et al. (2007) and Lysenko and D’Souza (2008)
• Summary: explores the use of GPU and GPU-based programming as a platform for ABMS
• How Repast HPC Differs: much more flexible programming model

5.4 FROM REPAST S TO REPAST HPC

Repast is a widely used ABMS toolkit.⁴ Multiple versions of the toolkit have been created, the latest of which is Repast Simphony for Java (Repast SJ). Repast SJ is a pure Java ABMS platform whose architectural design is based on central principles important to agent modeling. These principles combine findings from many years of ABMS toolkit development and from experience applying the ABMS toolkits to specific applications. More details on Repast Simphony are reported by North et al. (2007).

The parallel C+ implementation of Repast (Repast HPC) attempts to preserve the salient features of Repast SJ while adapting them for parallel computation in C++. More specifically,

• agents are naturally represented as objects (in the object-oriented programming sense);
• scheduling is flexible and dynamic; and
• implementation should be driven by modeling rather than framework requirements; model components (e.g., agents) should be “plain old objects” as far as possible.

These requirements are considered in detail in the remainder of this section.

5.4.1 Agents as Objects

An agent’s internal state (e.g., its age and wealth) is easily represented in an object’s fields while the agent’s behavior (e.g., eating, aging, and acquiring and spending wealth) is modeled using an object’s methods. Implementing agents as objects is most easily done using an object-oriented language. Consequently, Repast HPC is implemented in C++. Using C++ also allows us to take advantage of the Standard Template Library (STL) as well as sophisticated third-party libraries such as Boost.⁵

5.4.2 Scheduling

Repast Simphony simulations are driven by a discrete-event scheduler. Events themselves are scheduled to occur at a particular tick. Ticks do not necessarily represent clock time but rather the priority of its associated event. Ticks determine the order in which events occur with respect to each other. For example, if event A is scheduled at tick 3 and event B at tick 6, event A will occur before event B. Assuming nothing is scheduled at the intervening ticks, A will be immediately followed by B. There is no inherent notion of B occurring after a duration of three ticks. Of course, ticks can and are often given some temporal significance through the model implementation. A traffic simulation, for example, may move the traffic forward 30 seconds for each tick. A floating point tick, together with the ability to order the priority of events scheduled for the same tick, provides for flexible scheduling. In addition, events can be scheduled dynamically on the fly such that the execution of an event may schedule further events at that same tick, or some future tick.

5.4.3 Modeling

Repast Simphony attempts to separate framework concerns from modeling concerns by eliminating implementation requirements such as interfaces or abstract base classes on the model side. Agents need not implement any interfaces or extend any parent classes in order to participate in the framework. Historically, agent-based models have maintained a tight coupling between individuals, their behaviors, and the space in which they interact. As a result, many models have been designed in a way that limits their ability to express behaviors and interactions. For example, an agent may have to implement a network node interface in order to participate as a node in a network, or a grid element interface in order to participate in a grid, or both to participate in both a network and a grid. Such coupling of the agent to the space in which it participates reduces flexibility and reuse, adds an undue implementation burden, and diverts focus from the actual model.

Repast Simphony’s approach avoids these problems and encourages flexibility and reusability of components and models through the use of contexts and projections. The context is a simple container based on set semantics. Any type of object can be put into a context, with the simple caveat that only one instance of any given object can be contained by the context. From a modeling perspective, the context represents a population of agents. The agents in a context are the population of a model. However, the context does not inherently provide any mechanism for interaction between the agents. Projections take the population as defined in a context and impose a new structure on it. The structure defines and imposes relationships on the population using the semantics defined in the projection. Projections have a many-to-one relationship with contexts. Each context can have an arbitrary number of projections associated with it. Projections are designed to be agnostic with respect to the agents to which projections provide structure. Actual projections are such things as a network that allows agents to form network-type relations with each other or a grid-type space where each agent is located in a matrix-type space (Howe et al., 2006).

Repast HPC attempts to preserve these features and principles as far as possible. Repast HPC has additional goals, driven by ease of use, namely,

• Users of the framework should be able to work with projections and agents as such, rather than more typical parallel friendly types: arrays, primitives, and so forth.
• Similarly, the details of parallelization (e.g., MPI-related calls) should be hidden from the client programmer (i.e., the user) as much as possible.

5.5 PARALLELISM

In parallelizing Repast for large-scale distributed platforms, our focus is on parallelizing the simulation as a whole rather than enabling the parallelization of individual agent behaviors across processors.⁶ The expectation, then, is that the typical simulation will contain either relatively few heavy, computationally complex agents per process or a multitude of lighter-weight agents per process. Processes communicate, share agents, and so forth using the MPI.

Each individual process is responsible for some number of agents local to that process. These agents reside in the memory associated with that process and the process executes the code that represents these local agents’ behavior. In terms of the Repast HPC components, each process has a scheduler, a context and the projections associated with that context. At each tick, a process scheduler will execute the events scheduled for that current tick, typically some behavior of the agents in the context that makes use of a projection. For example, each agent in a context might examine its network neighbors and might take some action based on those links, or each might examine its grid surroundings and move somewhere on the grid based on what it finds.

Processes do not exist in isolation. The schedule is synchronized across processes and data production and collection can be aggregated across all processes. More importantly, copies of nonlocal agents (i.e., agents whose own behavior is initiated by another process schedule) may reside on a process. These nonlocal agents may be used by the local agents as part of their behavior but are not under the control of the executing process. For example, agents can participate in a shared network that spans processes such that a link may exist between local and nonlocal processes.

Figure 5.1 shows a link between agent A1 and agent B2. A1 resides on process P1 and B2 on process P2. However, this cross-process link does not actually exist as such. A copy of B2 exists on P1 and A1 links with that. A1 can then query its network neighbors when its behavior is executed.

Figure 5.1 Agent A1 with a network link across processes to agent B2.

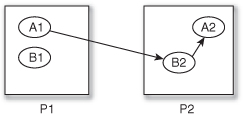
When copies of agents can be shared across processes, it is then necessary to synchronize the copies with the original agents. This applies both to an agent’s state (its properties and so forth) but also to its status (whether it is “alive,” “dead,” or has migrated among processes). If, for example, in the course of its behavior, an agent “dies,” then it should be removed from the simulation as a whole. Such synchronization requires a way to uniquely identify an agent without which there is no way to map copies to their originals. The AgentId serves this function.

class AgentId {

 … 

 int id_, startProc_, agentType_, currentProc_;

 std::size_t hash;

 … 

};

An AgentId is immutable with respect to its id_, startProc_ as well as agentType_ fields. The agentType_ field should identify the type of agent. For example, in a predator prey model, a constant value of 0 might identify the predator agents, and a value of 1 might identify the prey agents. The field startProc_ identifies the process rank on which the agent with this AgentId was created. Lastly, id_ is used to distinguish between agents of the same type created on the same process. Prey 2 created on process 3 is distinguished from prey 3 created on process 3, for example. Taken together, these three values should uniquely identify an agent across the entire simulation. The hash field is also immutable and is calculated based on the id_, startProc_ and agentType_ fields and is used as a key value when using agent objects in hash-based maps. The last field, currentProc_, is the process where the agent currently resides. Initially, this is the same as the agent’s starting process (startProc_) but may change if the agent moves between processes.

Every agent in the simulation must implement a getAgentId method that returns the AgentId for that agent. Using the AgentId, processes can request specific agents from the process where the agent resides and can then update their local copy with the canonical version. Similarly, if an agent dies and is removed from the simulation, the AgentId of the dead agent is sent to the relevant processes, allowing them to remove the agent from their contexts, projections, and so on. The actual process of requesting and synchronizing agents is handled by the RepastProcess component that is further discussed in greater detail.

5.6 IMPLEMENTATION

To implement its core parallelism, Repast HPC uses the Boost.MPI library⁷ and the MPI C++ API where necessary. Boost.MPI applies a more modern C++ interface to the MPI C and C++ API. Boost.MPI provides better support for modern C++ development styles and includes complete support for user-defined data types and C++ Standard Library types. The use of Boost.MPI is also an advantage for the client programmer, especially in the creation of MPI data types for user-defined data types such as agents. This helps to keep the focus on modeling concerns rather than on framework requirements.

The remainder of this section discusses the core components of Repast HPC and their implementation in more detail.

5.6.1 Context

The context component is a simple container based on set semantics that encapsulates an agent population. The equivalence of elements is determined by the AgentId. Each process has at least one context to which local and nonlocal agents are added and removed. The context component provides iterator implementations that can be used to iterate over all the agents in the context or only those that are local to the current process. Projections (Grids and Networks) are also contained by the context such that any agent added to a context becomes a member of the associated projections (e.g., occupying a grid cell or becoming a node in a network).

5.6.2 RepastProcess

The RepastProcess component encapsulates a process and manages interprocess communication and simulation state synchronization. Implemented as a singleton together with related template functions, a single RepastProcess exists per process. The RepastProcess exposes such data as a process rank and the total number of processes. Using the RepastProcess component, a client programmer can request copies of agents from other processes and can synchronize the state and status (i.e., alive, dead, or migrated) of requested agents.

AgentRequest request(myRank);

// get 10 random agents from other process

for (int i = 0; i < 10; i++) {

 AgentId id = createRandomId();

 request.addRequest(id);

}

repast::requestAgents<AgentContent>(provider, receiver);

This piece of code illustrates a request for agents. Requests are made using the AgentRequest object to which the IDs of the requested agents are added. This request is then passed to a template function, requestAgents. The function is specialized to provide and receive the type AgentContent. The provider and receiver, which are themselves type parameters, are responsible for providing the content to the requesting process and for receiving the requested content. The user is responsible for coding the provider and the receiver, but this requires only the implementation of a single method each. The provider typically retrieves the content from agents in the context using the IDs of the requested agents, while the receiver typically creates the agents from the requested content and then adds them to the context.⁸

The relevant dynamic content or state of an agent can typically be described by a struct or class of primitive types. The client programmer specializes the requestAgents method for this struct or class (e.g., the AgentContent type in the above-mentioned example). More importantly, Boost.MPI transparently constructs the necessary MPI data types for such a struct or class and can efficiently pass (send, recv, broadcast, etc.) them among processes. The amount of work that the client programmer needs to do is fairly trivial; most of the work is done by the RepastProcess component and Boost.MPI.

Implementation-wise, the sending and receiving of agent content using the RepastProcess component works as follows: Nonroot processes send their requests to the root process (the process with rank 0). The root process sorts these requests as well as any of its own by the containing process, that is, by the process on which the requested agent resides. For example, if P1 requests Agent A from P2, P0 requests B from P2, and P3 requests C from P1, then P0 (the root process) sorts these three requests into two lists: the agents requested from P2 (A and B) and the agents requested from P1 (C). The root process then sends these request lists to the process that can fulfill them. These processes then fulfill the requests by extracting the content of the requested agents and then sending that content to those processes that initiated the request. Throughout this mechanism, RepastProcess tracks the agent content that it is importing from other processes and the agent content it is exporting to other processes. Synchronization of state and status is then easily done by sending and receiving the canonical state and status changes between the associated importing and exporting process pairs.

5.6.3 Scheduler

Repast HPC uses a distributed discrete-event scheduler that is, at least in the current implementation, tightly synchronized across processes. In this, it has more in common with conservative PDES synchronization algorithms as discussed earlier (Chandy and Misra, 1979, 1981). Earlier work on parallel simulation demonstrates the effectiveness as well as the complexities of optimistic and mixed-mode scheduling (Jefferson et al., 1987; Jha and Bagrodia, 1994; Perumulla, 2005; Perumulla, 2007). The initial implementation of the Repast HPC scheduler avoids these complexities and leaves room for implementing more advanced parallel scheduling algorithms in the future.

MethodFunctor<NetworkSim>*

 mf = new MethodFunctor<NetworkSim> (this, &NetworkSim::step); scheduler.scheduleEvent(1, 1, mf);

…

scheduler.scheduleStop(100);

The scheduler schedules MethodFunctors, that is, method calls on objects, using the tick-based scheme described in Section 5.4. MethodFunctors can be scheduled to execute once at a particular tick or by starting at a particular tick and then repeating at a regular interval. The scheduler also has additional methods for scheduling simulation termination as well as methods for scheduling events that should occur post-termination. These last events are particularly useful for finishing data collection, cleaning up open resources, and so forth. The code mentioned earlier illustrates a typical piece of scheduling code. The step method on a NetworkSim object is scheduled to execute at tick 1 and then every tick thereafter, and the simulation itself is scheduled to terminate at tick 100.1.

The scheduler runs in a loop until the stop event is executed. At each iteration of the loop, the scheduler determines the next tick that should be executed, pops the events for that tick-off of a priority queue, and executes any MethodFunctors associated with those events. The scheduler synchronizes across processes when it determines the next tick to execute. Each individual scheduler on each process passes the next tick it will execute to an “all_reduce” call and receives the global minimum next tick as a result. If this global minimum is equal to the local next tick, then the local scheduler executes. Synchronization is thus twofold: (1) The “all_reduce” call is a barrier preventing individual processes from getting too far ahead or too far behind; (2) by only executing the global minimum tick, we insure that all processes are executing the same tick. This type of synchronization is, of course, restrictive and implies that each process is under a similar load and that the coherency of the simulation as a whole benefits from such synchronization. Future work will examine relaxing the synchronization through checkpointing, rollbacks, and so forth. This type of tight synchronization, however, does fit reasonably well with many types of currently implemented agent simulations.

5.6.4 Distributed Network

The distributed network component implements a network projection that is distributed over the processes in the simulation. Each process is responsible for the part of the network in which its local agents participate as nodes. However, these local agents may have network links to nonlocal agents (or rather copies of them as described earlier) and through them to those parts of the network on other processes. The distributed network provides typical ABMS network functionality: retrieving network node successors and predecessors, creating and removing edges, and so forth.

The design of the distributed network is guided by the notion that each process should only see as much of the network as necessary for the behavior of the local agents. For example, if an agent’s behavior incorporates only its immediate network neighbors, then only these neighbors need be present on the local process. There is no need for a larger view of the network incorporating neighbors of neighbors, and other features. The extent of the larger network that is visible to a process is thus configurable by the user. In particular, the distributed network includes methods for creating complementary edges across processes as well as for mirroring the relevant linked parts of the larger network into an individual process.

The creation of complementary edges works much like the sharing of agents previously described. For example, Process 1 (P1) creates an edge between A1 and B2 where B2 is a copy of an agent from Process 2 (P2). Initially, P2 has no knowledge of this edge until P1 informs P2, and P2 creates the complementary edge (A1 → B2) on its copy of the network. As part of edge creation, the distributed network tracks those edges that require a complement to be created and the process on which they should be created. A list of these processes is sent to the root process. The root process sorts these lists such that a list of processes from which to expect a complementary edge can be sent to each process. Each process then asynchronously sends and receives the complementary edges. These edges are then incorporated into the local copy of the network. Copies of nonlocal agents may be received together with the edge (e.g., P2 receives a copy of A1, mentioned earlier), and these copies are then added to the local context as well as to the RepastProcess’ relevant import and export lists.

Acquiring additional parts of the network works in much the same way. Edges are sent and received, although the initial request is, of course, not for complementary edges but for additional nodes in the network.

5.6.5 Distributed Grid

The distributed grid projection implements a discrete grid where agents are located in a matrix-type space. It implements typical ABMS grid functionality: moving agents around the grid, retrieving grid occupants at particular locations, getting neighbors, and so forth. The grid is distributed over all processes, and each process is responsible for some particular subsection of the grid (see Fig. 5.2). The agents in that particular subsection are local to that process. Grids are typically used to define an interaction topology between agents such that agents in nearby cells interact with each other. In order to accommodate this usage, a buffer can be specified during grid creation. The buffer will contain nonlocal neighbors, that is, agents in neighboring grid subsections. Grid creation leverages MPI_Cart_create so that processes managing neighboring grid subsections can communicate efficiently.

Figure 5.2 Distributed grid. P1 manages grid cells (0, 0)–(2, 3), P2 manages (3, 0)–(5, 3), and so on.

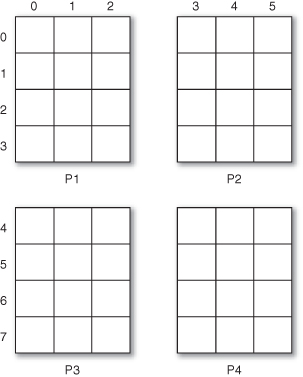
The distributed grid also allows agents to move out of one grid subsection and into another. This entails migrating the agent from one process to another in order to minimize the nonlocal knowledge (and thus the synchronization overhead) that each process requires. The distributed grid works in conjunction with a RepastProcess to achieve this interprocess agent movement. Note that this can become quite involved if the agent or copies of the agent are referenced in other processes.

5.6.6 Data Collection and Logging

Repast HPC implements two kinds of data collection: aggregate and nonaggregate. Aggregate data collection uses MPI’s reduce functionality to aggregate data across processes and writes the result into a single file using Network Common Data Form (NetCDF⁹). The details of MPI and NetCDF are invisible to the user, however. The user specifies numeric data sources and the reduction operation to apply to the data produced from those sources. These data sources are then added to a DataSet object, associating the data sources with identifying names. The resulting data are two dimensional: Each column corresponds to a data source and each row to the time (tick) at which the data were recorded. The data itself are retrieved from implementations of a templated interface with a single getData method. The type (int or double) of the data returned is determined by the template specialization. The actual recording and writing of data is done through scheduled events. Boost.MPI is particularly helpful here in that it allows the use of the STL C++ algorithms as reduction operations and makes it relatively easy to create custom operations.

Nonaggregate data collection works in much same the way, except that no reduce operation is specified. The resulting data are three dimensional with the process rank acting as the third dimension.

Repast HPC also implements a more generic logging framework along the lines of the popular Java Log4J library.¹⁰ The user defines appenders and loggers. Appenders determine where logged data can be written: stderr, stdout, or to a file(s). A logger combines one or more appenders and a logging level. Any data written to a logger with a level greater than or equal to the logger’s log level will then be time-stamped and written to that logger’s appenders. Repast HPC creates a default logger for each process that can be used to systematically log debug info, errors, and so forth.

5.6.7 Random Number Generation and Properties

Repast HPC provides centralized random number generation via a random singleton class. Random leverages Boost’s random number library, using its implementation of the Mersenne Twister (Matsumoto and Nishimura, 1998) for its pseudorandom number generator. Uniform, triangle, Cauchy, exponential, normal, and log normal distributions are available. Random is not distributed across processes, but rather, individual instances execute on individual processes. Our experience with Repast and agent simulation in general has illustrated the usefulness of a singleton-based random number implementation, especially with respect to replicating results. Repast HPC thus follows this model.

The random seed can be set either in the code itself or by using a simple properties file format. The canonical Repast HPC executable expects a -config option that names a properties file. Specific random number properties in that file are then used in the initialization of the random class. A properties file has a simple key = value format. An example of random number-related properties is

random.seed = 1

distribution.uni_0_4 = double_uniform, 0, 4

distribution.tri = triangle, 2, 5, 10

The random.seed property specifies the seed for the generator. If no seed is specified, then the current calendar time is used (i.e., the result of std::time(0)). Distributions can be created and labeled by specifying a distribution property. The keys for such properties begin with distribution followed by a “.” and then a name used to identify the distribution for later use. The value of the property describes the type of the distribution and any parameters it might take. For example, the piece of code starting with random.seed = 1 creates a distribution named “tri.” It is a triangle distribution with a lower bound of 2, a most likely value of 5, and an upper bound of 10. This distribution can be used in the model by retrieving it by name (“tri”) from the Random class.

In addition to providing easy random number configuration, properties and properties files also provide support for arbitrary key/value pairs. These can be parsed from the properties file itself or added at run time to a Properties object. The Properties class provides this functionality. The canonical main function used by a Repast HPC model will pass the properties file to the Properties class constructor and will then make this Properties object available to the model itself. Model parameters will typically be set in properties files, making it trivial to change a model’s parameters without recompilation.

5.7 EXAMPLE APPLICATION: RUMOR SPREADING

As a benchmark application and equally importantly to determine, if only informally, Repast HPC’s ease of use and how well modeling concerns are separated from framework concerns, we have written a simple rumor-spreading application. The application models the spread of a rumor through a networked population. The simulation proceeds as follows. As part of initialization, some numbers of nodes are marked as rumor spreaders. At each iteration of the simulation, a random draw is made to determine if the neighbors of any rumor-spreading nodes have received the rumor. This draw is performed once for each neighbor. After all of the neighbors that can receive the rumor have been processed, the total number of nodes that have received the rumor is recorded. We hope that this initially simple model can become the basis for more thorough investigations of network topologies in related models, such as the spread of trends through a population, the role of “influencers” or trendsetters in such, and the spread of epidemics in general. The potential value of using such virtual “worlds” to generate data for testing analysis techniques is documented by Zurell et al. (2010). In particular, they describe the role of virtual data in evaluating methods for data sampling, analysis, and modeling methods with respect to ecology and ecological models.

The network itself is created using the KE model for growing networks. Klemm and Egužluz (2002) demonstrated a model for creating networks that display the typical features of real-world networks: power law distribution of degree and linear preferential attachment of new links. More importantly, the KE model creates networks with degree distribution similar to the preferential attachment model of Barabási and Albert (1999) but also includes other network topology features more like those found in real computer networks.

The KE model generates the network as follows. As an initial condition, there is a fully connected network of m active nodes. A new node, i, is added to the network. An outgoing link is created between i and each of the active nodes. Each node j of the m active nodes thus receives exactly one incoming link. The new node i is added to the set of active nodes. One of the currently active nodes is then removed from the set of active nodes. The probability that a node is made inactive is inversely proportional to its current degree, k_i:

(5.1)

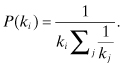
This is then repeated for each new node, i, that is to be added to the network (Briesemeister et al., 1998; Klemm and Eguíluz, 2002).

We have adapted this to the distributed context by sharing n number of nodes between processes. Prior to network creation, each process requests n nodes at random from 4 “adjacent” processes. Adjacency here is determined by a process rank, such that a process with rank n is adjacent to ranks n − 1, n − 2, n + 1, and n + 2. When adjacent ranks are less than 0 or greater than the number of processes—1, the adjacent ranks are determined by wrapping either to the end or to the beginning. For example, given a process total of 128, process 0 is adjacent to 126, 127, 1, and 2. After importing the additional nodes, each process then builds a KE-model network using these shared nodes, together with nodes local to that process. Once the network has been built on each process, complementary edges are generated such that the edges created between shared and local nodes are then themselves shared across the relevant processes. For example, an edge is created on process one (P1) creates an edge between two nodes where the first node resides on process two (P2). Complementary edge creation will then create the corresponding edges between the corresponding nodes on P2. The resulting network is intended to roughly model more densely connected clusters of friends integrated into larger clusters of clusters.

As the simulation runs, each process maintains a list of the nodes that have currently received the rumor (so-called rumored nodes). This list includes both local and nonlocal shared nodes. At each iteration of the simulation, we iterate through this list and attempt to pass on the rumor, via random draws, to the neighbors of these rumored nodes. These neighbors, however, must be local to the executing process in order for the rumor attempt to be made. This avoids any race conditions with respect to whether or not a node has received the rumor and the necessity for any potentially time-consuming resolution of conflicting state. The state of shared nodes is updated after processing the neighbors. Any change in the rumor state of nonlocal shared nodes is thus communicated among processes and the list of rumored nodes is updated to include any newly “rumored” nonlocal shared nodes. In this way, the integrity of the network with respect to spreading the rumor via cross-process links is preserved.

The simulation has the following parameters:

These parameters are contained in a Repast HPC properties file together with named distributions and an initial random seed. The seed is shared among all processes, allowing for repeatable results.

The implementation of the model, of course, uses the various components described previously, the RepastProcess, the distributed network, and so forth. Consequently, the nodes are modeled agents and the edges themselves are instances of the RepastEdge class. No doubt this thoroughly object-oriented implementation imposes some overhead, but it does have significant advantages with respect to expanding and improving the model. For example, if the spread of a rumor between two nodes becomes dependent on the strength of the tie between them or on some property of the nodes themselves, then the changes to the code are easy to implement.

The code itself was developed on Mac OSX using Open MPI. Benchmark runs and additional testing were performed on an IBM Blue Gene/P 1028 processor system hosted by Argonne National Laboratory’s Leadership Computing Facility. Blue Gene’s native compiler, bgxlc++, was used to compile the relevant parts of Boost and the Repast HPC code.

5.7.1 Performance Results

The model was run with the following parameters. The probability of a node receiving a rumor was set to 0.01, and the draw was made from a uniform distribution (0, 1). Ten nodes were marked as initial rumored nodes. The number of nodes n shared between adjacent processes was set to 40, and the KE model m parameter was set to 10. Each run iterated for 200 ticks (iterations). Run times were measured for both initialization (agent creation, network setup, initial sharing of node, and edges) as well as the time to complete 200 iterations.

Figure 5.3 illustrates the total run time (initialization plus the time to complete 200 iterations) for varying network node counts grouped by process count. We can see a trade-off between the benefit of running smaller numbers of agents (network nodes) on each process and the cost of interprocess communication. The total run time for a 100-k node network on 256 processes is less than all the other process counts for the same sized network. As the network node count increases, the advantages of running smaller numbers of nodes on each process increases and runs on a larger number of processes become progressively faster. The lack of perfect weak scaling is obvious.

Figure 5.3 Total time by process count.

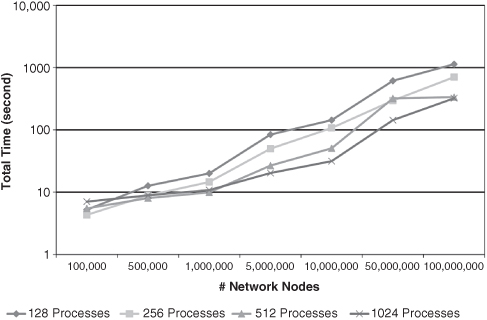
This trade-off is obviously model dependent. Our sample model is not computationally intensive, and thus the advantages of a larger number of processors do not appear at lower numbers of agents. Models with more computationally “thick” agents would presumably see a benefit with lower numbers of agents and equivalent numbers of processes. Similarly, models that require less interprocess communication would obviously be faster as well.

Figures 5.4 and 5.5 and Table 5.1 illustrate that the cause of the trade-off lies in the initialization of the model and less in its actual execution, that is, in the iteration and execution of the scheduled events. The initialization time for 1024 process runs is nearly 4.50 times slower when running 100-k agents than the 128 process run, even though each individual process is initializing 8× less agents. As mentioned earlier, initialization consists in part of sharing agents between neighboring processes. In terms of the Repast HPC components, this sharing is initiated using AgentRequests as described in Section 5.6.2. AgentRequests are coordinated by a root process (process rank 0). This root process sequentially receives all the requests sent by all the requesting nonroot processes. The time spent in this send and receive increases as the process count increases: The loop is longer; there is ultimately more interprocess communication and more requests for the root process to coordinate. Future work will investigate potential optimizations to the AgentRequests mechanism.

TABLE 5.1 Initialization and Run Times

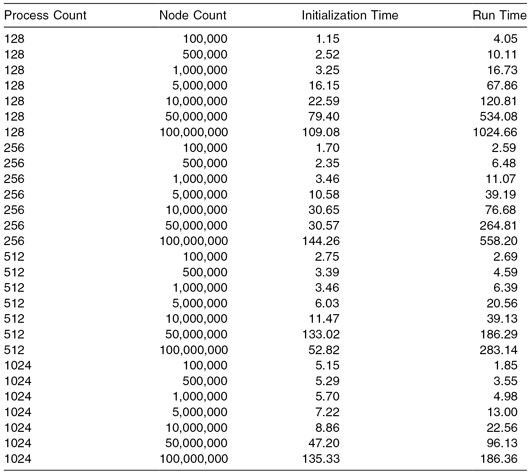
Figure 5.4 Initialization time by process count.

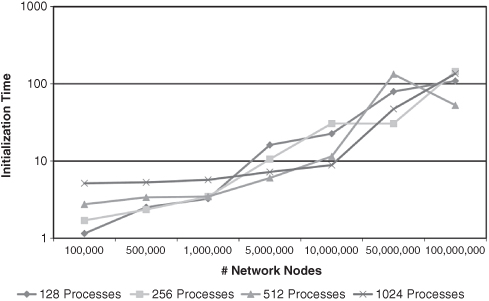
Figure 5.5 Iteration time by process count.

Absent the initialization overhead, the model and the Repast HPC components scale reasonably well. In all but one case, a greater number of processes lead to faster run times.¹¹ On average, twice as many processors for runs with the same number of nodes run 1.62 times as fast, with maximum increases of 2.00 times and minimum of 0.90 times, still shy of perfect weak scaling. There is some very small overhead associated with data collection that increases slightly as the number of processes increases, but the variations in scaling and the lack of perfect weak scaling are most likely due to variations in the simulated network configuration. The configuration will vary between model runs and within the processes themselves for a single-model run. More particularly, processes whose network configuration leads to a greater number of rumored nodes take longer to complete an iteration. This, in turn, increases the idle time of other processes during schedule synchronization as they wait for the slower process to complete. We also suspect that variations in network configuration are in part responsible for the lack of perfect weak scaling when the process count is constant and the number of agents is increased, for example, the anomalous spike for 512 processes when running 50 million agents. We hope to investigate the effects of network configuration further when expanding the rumor model.

Additional future work will investigate scaling beyond 1024 processes. Scaling is of course dependent on the trade-off described earlier, especially with respect to the cross-process sharing of agents, and thus partly on the model. Increasing the number of processes can further increase interprocess communication, and the optimum number of agents then changes. Ultimately though, given that many models cannot be run at all using current ABMS tools, the trade-off is not between faster and slower, but rather between running the model or not running it all.

5.8 SUMMARY AND FUTURE WORK

This chapter has presented an overview of the Repast HPC project and, more particularly, the implementation of the Repast HPC framework. The authors hope the framework can help to leverage the increasing computing capability made available on high-performance computing platforms by bringing this capability to ABMS. Throughout this chapter, we have tried to emphasize that our concern is with creating a useful and usable working system. In this, we differ from much of the related work in this area. Our experience with the implementation of previous Repast systems has taught us about the natural fit between agent-based modeling and object-oriented programming, the importance of flexible and dynamic scheduling, and, perhaps most importantly, that the implementation should be driven by modeling rather than by framework concerns. All these we have tried to carry over into the larger-scale distributed context.

In particular, the latter item informs the implementation of the RepastProcess, the distributed projections, and the scheduling implementation. The details of the parallel implementation and MPI are hidden behind a simpler API. Where parallel and distributed framework concerns are unavoidable, an effort has been made to make these more conceptually accessible by framing the documentation and API in terms of the executing process, local and nonlocal shared agents. The source code of the example rumor model application neatly reflects this. The intention of the model itself is easily discernable and the parallel or distributed parts of the code are most naturally interpreted in terms of executing process, local and nonlocal shared agents. Future work will focus on expanding the rumor model, developing additional models using the framework, and on improvements to and experiments with the framework itself. The intent is to fill existing gaps and to leverage the excellent existing work in parallel with discrete-event scheduling to improve the scheduling architecture. The simple sample rumor model has illustrated the trade-off between agent population size and interprocess communication. Future work will attempt to minimize this trade-off, allowing for scaling to a larger number of processes with equivalent-sized agent populations.

Notes

1 http://drone.sourceforge.net.

2 The SISC’s IEEE Standard for Modeling and Simulation (M&S) High Level Architecture (HLA)—Framework and Rules.

3 http://www.fipa.org.

4 http://repast.sourceforge.net.

5 http://www.boost.org.

6 The latter could be done, of course, either through a model-specific scheme or by conceptualizing the agent behavior as kind of pseudosimulation and by using Repast HPC’s functionality.

7 http://www.boost.org/docs/libs/1_39/doc/html/mpi.html.

8 Future work should capture this typical case such that the client programmer would only have to provide the provider and receiver if he or she needs more than simple add and retrieve from the context.

9 http://unidata.ucar.edu/software/netcdf.

10 http://logging.apache.org.

11 The exception is the 100-k node run where 256 processes run 0.10 seconds faster than 512.

REFERENCES

R. L. Bagrodia and W. Liao. Parallel simulation of the Sharks World problem. In Proc. of the 22nd Winter Simulation Conference, pp. 191–198, 1990.

A. Barabási and R. Albert. Emergence of scaling in random networks. Science, 286(5439):412–413, 1999.

D. W. Bauer, C. D. Carothers, and A. Holder. Scalable time warp on Blue Gene supercomputers. In 2009 ACM/IEEE/SCS 23rd Workshop on Principles of Advanced and Distributed Simulation, pp. 35–44, 2009.

J. Bradshaw. KAoS: An open agent architecture supporting reuse, interoperability, and extensibility. In Proc. of the 1996 Knowledge Aquisition Workshop, 1996.

L. Briesemeister, P. Lincoln, and P. Porras. Epidemic profiles and defense of scale-free networks. In Proc. of the 2003 ACM Workshop on Rapid Malcode, 1998.

C. D. Carothers, D. W. Bauer, and S. O. Pearce. ROSS: A high-performance low memory, modular time warp system. Journal of Parallel and Distributed Computing, 62(11):1648–1669, 2002.

K. M. Chandy and J. Misra. Distributed simulation: A case-study in design and verification of distributed programs. IEEE Transactions on Software Engineering, SE(5):440–452, 1979.

K. M. Chandy and J. Misra. Asynchronous distributed simulation via a sequence of parallel computations. Communications of the ACM, 24(4):198–205, 1981.

R. M. D’Souza, M. Lysenko, and K. Rahmani. SugarScape on steroids: Simulating over a million agents at interactive rates. In Proc. of the Agent 2007 Conference on Complex Interaction and Social Emergence, 2007.

S. Deissenberg and H. van der Hoog. EURACE: A massively parallel agent-based model of the European economy. Technical report, Universites d’Aix-Marseille, 2009. halshs.archives-ouvertes.fr/docs/00/33/97/56/PDF/ DT2008-39.pdf.

R. M. Fujimoto. Parallel discrete event simulation. Communications of the ACM, 33(10):30–53, 1990.

R. M. Fujimoto. Parallel and Distributed Simulation Systems. Piscataway, NJ: Wiley Interscience, 2000.

N. Houari and B. H. Far. Building collaborative intelligent agents: Revealing main pillars. In Proc. of the Canadian Conference on Electrical and Computer Engineering, 2005.

T. R. Howe, N. T. Collier, M. J. North, et al. Containing agents: Contexts, projections and agents. In Proc. of the Agent 2006 conference on social agents: Results and prospects, 2006.

P. Hudak. Conception, evolution, and application of functional programming languages. ACM Computing Surveys, 21(3):359–411, 1989.

D. R. Jefferson. Virtual time. ACM Transactions of Programming Languages and Systems, 7(3):404–425, 1985.

D. Jefferson, B. Beckman, F. Wieland, et al. Time warp operating system. ACM SIGOPS Operating Systems Review, 21(5):77–93, 1987.

V. Jha and R. Bagrodia. A unified framework for conservative and optimistic distributed simulation. ACM SIGSIM Simulation Digest, 24(1):12–19, 1994.

H. Karimabadi, J. Driscoll, J. Dave, et al. Parallel discrete event simulation of grid-based models: Asynchronous electromagnetic hybrid code. Springer Verlag Lecture Notes in Computer Science, 3732:573–582, 2006.

K. Klemm and V. Egužluz. Highly clustered scale free networks. Physical Review E, 65(036123):1–6, 2002.

M. T. Koehler and B. F. Tivnan. Clustered computing with NetLogo and Repast J: Beyond chewing gum and duct tape. In Proc. of the Agent 2005 Conference on Generative Social Processes, Models, and Mechanisms, pp. 43–54, 2005.

Y.-K. Kwok and K.-P. Chow. On load balancing for distributed multiagent computing. IEEE Transactions on Parallel and Distributed Systems, 13(8):787–801, 2002.

G. Laycock. The theory and practice of specification based software testing. PhD thesis, University of Sheffield, 1993.

M. Lysenko and R. M. D’Souza. A framework for meagascale agent-based model simulations on graphical processing units. Journal of Artificial Societies and Social Simulation, 11(4), 2008. Available at http://jasss.soc.surrey.ac.uk/11/4/10.html.

F. Massaioli, F. Castiglione, and M. Bernashci. OpenMP parallelization of agent-based models. Parallel Computing, 31(10–12):1066–1081, 2005.

M. Matsumoto and T. Nishimura. Mersenne Twister: A 623-dimensionality equdistributed uniform psuedo-random number generator. ACM Transactions on Modeling and Computer Simulation: Special Issue on Uniform Random Number Generation, 8(1):3–30, 1998.

D. M. Nicol and S. E. Riffe. A “conservative” approach to parallelizing the Sharks World simulation. In Proc. of the 22nd Winter Simulation Conference, 1990.

M. J. North and C. M. Macal. Managing Business Complexity: Discovering Strategic Solutions with Agent-Based Modeling and Simulation. New York: Oxford University Press, 2007.

M. J. North, E. Tatara, N. T. Collier, et al. Visual agent-based model development with Repast Simphony. In Proc. of the Agent 2007 Conference on Complex Interaction and Social Emergence, 2007.

T. Oguara, D. Chen, G. Theodoropoulos, et al. An adaptive load management mechanism for distribution simulation of multi-agent systems. In Proc. of the 9th IEEE Int’l Symposium on Distributed Simulation and Real-Time Applications, 2006.

K. S. Perumulla. μsik—a micro-kernel for parallel/distributed simulation systems. In Workshop on Principles of Advanced and Distributed Simulations, 2005.

K. S. Perumulla. Parallel and distributed simulation: Traditional techniques and recent advances. In Proc. of the Winter Simulation Conference (WSC), 2006.

K. S. Perumulla. Scaling time warp-based discrete event execution to 10⁴ processors on a Blue Gene supercomputer. In Proc. of the 4th Int’l Conference on Computing Frontiers, pp. 69–76, 2007.

M. T. Presley, P. L. Reiher, and S. F. Bellenot. A time warp implementation of the Sharks World. In Proc. of the 22nd Winter Simulation Conference, pp. 199–203, 1990.

M. Scheutz, P. Schermerhorn, R. Connaughaton, et al. SWAGES: An extendable distributed experimentation system for large-scale agent-based a life simulations. In Proc. of the 10th Int’l Conference on the Simulation and Synthesis of Living Systems, 2006.

D. Zurell, U. Berger, J. S. Cabral, et al. The virtual ecologist approach: Simulating data and observers. Oikos—A Journal of Ecology, 119(4):622–635, 2010.