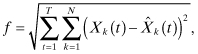8.1 INTRODUCTION

This chapter is concerned with modeling and simulating the dynamics of gene regulatory networks (GRNs). Gene regulation refers to processes that cells use to create functional gene products, in particular proteins, from the information stored in genes. Gene regulation is essential for life as it increases the versatility and adaptability of an organism by allowing it to express or synthesize protein when needed. While aspects of gene regulation are well understood, many open research questions still remain (Davidson and Levin, 2005).

The modeling of dynamic biomedical phenomena such as gene regulation is inspired by the approach taken in physics, where models are frequently constructed to explain existing data, then predictions are made, which again are compared to new data. If a sufficient correspondence exists, it is claimed that the phenomenon has been understood. The ability to construct, analyze, and interpret qualitative and quantitative aspects of gene-regulation models is becoming increasingly important (Hasty et al., 2001). In contrast to static gene expression data, the use of dynamic gene expression data with modeling and simulation helps to determine stable states of gene regulation in response to a condition or stimulus as well as the identification of pathways and networks that are activated in the process.

In this chapter, we study the process of reverse-engineering GRNs from time-series gene expression data sets. The idea is to discover an optimal set of parameters for a computational model of the network that is able to adequately simulate the behavior described by the gene expression data sets. We investigate three different mathematical methods used in computational models that are based on ordinary differential equations. Each system of differential equations has its own characteristics, which lead to biases and artifacts in the network models (Swain et al., 2010). We apply these three mathematical methods to a recent biological data set generated by Cantone et al. (2009) specifically for in vivo assessment of reverse-engineering and gene network modeling approaches. The model network presented by Cantone et al. (2009) is a relatively small network. However, such small GRNs can display complex nonlinear behavior due to the various positive and negative feedback loops that may exist between genes in the network.

The mathematical models we investigate require a significant number of parameters to be fine-tuned in order for the models to accurately simulate real biological network behavior. This is a combinatorial optimization problem that often requires considerable computational resources depending on the size and complexity of the network being investigated. We use a reverse-engineering method based on evolutionary algorithms to search through the parameter space and to optimize the values of the parameters in the mathematical models. In the models, there are at least four parameters to be optimized per gene in the network. Each gene may influence the behavior of other genes in the network in complex ways that depend on the nature of the feedback loops. In addition, depending on the mathematical model used, very small variations in a single parameter value can have quite a dramatic effect on the overall network behavior. There may therefore be a great variation in the quantity of computing power required to optimize parameter values in different networks and in different mathematical models. In order to take advantage of available computational resources, we have implemented our parallel evolutionary algorithms using QosCosGrid-OpenMPI (QCG-OMPI).

QCG-OMPI was designed to enable parallel applications to run across widely distributed computational resources owned and secured by different administrative organizations (Coti et al., 2008). The QCG-OMPI middleware is described further in Chapter 9 of this book. An important feature of QCG-OMPI that we have used in this study is its ability to support topology-aware applications: Just as complex dynamical systems may consist of many interdependent physical parts, it is also possible that computational models of complex dynamical systems can be decomposed into interdependent functional components that together comprise a topology-aware application; the connections between these components define a specific topology that can be matched to the distributed resources available on a computational grid infrastructure. Topology-aware middleware, such as QCG-OMPI, are designed to efficiently support the process of matching topology-aware applications to available networked resources.

This chapter is organized as follows. First, we describe our reverse-engineering methodology in detail, including the different mathematical methods, our optimization approach, and QCG-OMPI. Our results section is divided into two subsections, the first describing how the application scales over distributed resources geographically separated by hundreds of kilometers, and the second demonstrates the accuracy of models reverse engineered using the different mathematical methods. Finally, we conclude with a summary of our main results.

8.2 METHODOLOGY

In this section, we first describe a small synthetic GRN in yeast (Cantone et al., 2009) that we used in our reverse-engineering studies. Subsequently, we outline three systems of equations generally used for modeling GRNs. We then describe QCG-OMPI, which is the novel topology-aware Message Passing Interface (MPI) that we used to implement the communications in our application, and finally, we give the details of our particle swarm optimization (PSO) method that we applied to the problem of reverse-engineering GRNs.

8.2.1 Modeling GRNs

The strengths and weaknesses of the mathematical methods are highlighted by using the methods to reverse engineer a real biological network.

8.2.1.1 Case Study: A Yeast Synthetic Network

Cantone et al. (2009) synthetically constructed a GRN in yeast to facilitate an in vivo assessment of various reverse-engineering and gene network modeling approaches, including approaches based on ordinary differential equations.

Cantone et al. (2009) present expression profiles of the network genes after a shift from a glucose-containing medium to a galactose-raffinose-containing medium; this is called the switch-on time series; and after a shift from galactose-raffinose to glucose-containing medium: the switch-off time series. In this study, we used the first 100 minutes of these two data sets, excluding the first 10-minute interval during which the washing steps and the subsequent medium shift are performed. After 100 minutes, the biological system is perturbed, and Cantone et al. (2009) used time-delay terms to model this perturbation, which are not present in the basic forms of the equations we study here.

The network includes a variety of regulatory interactions, thus capturing the behavior of larger eukaryotic gene networks on a smaller scale. It was designed to be minimally affected by endogenous genes and to transcribe its genes in response to galactose. While the yeast GRN appears relatively small (see Fig. 8.1), it is actually quite articulated in its interconnections, which include regulator chains, single-input motifs, and multiple feedback loops.

Figure 8.1 The yeast synthetic network presented by Cantone et al. (2009), with the activating ↑ and repressing ⊥ regulatory interactions.

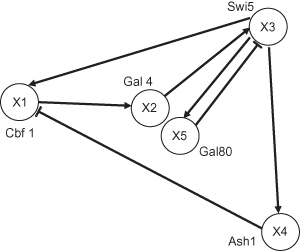
When reverse engineering this GRN, we assume the basic topology of the network; that is, we know which genes are connected, although we do not know if the type of interaction is activating or repressing. The optimization method we use (see Section 8.2.3) then estimates the parameters of a mathematical method. By numerically solving the differential equations with a set of parameters, we can simulate the dynamic behavior of the model, and if the output of our simulations precisely reproduce the time-series data sets recorded by laboratory scientists, then we can claim that our model has reverse engineered the GRN.

The nonlinear differential equations of the three modeling methods investigated in this study describe the mutual activating and repressing influences of genes in a GRN at a high level of abstraction. In particular, it is assumed that the rate of gene expression depends exclusively on the concentration of gene products arising from the nodes (genes) of the GRN. This means that the influence of other molecules (e.g., transcription factors) and cellular processes (translation) is not taken into account directly. Even with these limitations, dynamic GRN models of this kind can be useful in deciphering basic aspects of gene regulatory interactions.

The three methods we have studied have been widely used to model dynamic GRNs. One major advantage of all three methods lies in their simple homogeneous structures, as this allows the settings of parameter discovering software to be easily customized for these structures. In addition, all three modeling methods either already have the potential to describe additional levels of detail or their structures can be easily extended for this purpose.

The three methods describe dynamic GRN models by means of a system (or set) of ordinary differential equations. For a GRN comprising N genes, N differential equations are used to describe the dynamics of N gene product concentrations, X_i with i = 1, … , N. In all three methods, the expression rate dX_i/dt of a gene product concentration may depend on the expression level of one or more gene products of the genes X_j, with j = 1, … , N. Thus, the gene product concentration X_i may be governed by a self-regulatory mechanism (when i = j) or it may be regulated by products of other genes in the GRN.

In the following sections, we introduce the three mathematical modeling methods in some detail.

8.2.1.2 The Artificial Neural Network (ANN) Method

Vohradsky (2001) introduced ANN as a modeling method capable of describing the dynamic behavior of GRNs. The way this method represents and calculates expression rates depends on the weighted sum of multiple regulatory inputs. This additive input processing is capable of representing logical disjunctions. The expression rate is restricted to a certain interval where a sigmoidal transformation maps the regulatory input to the expression interval. ANNs provide an additional external input, which has an influence on this transformation in that it can regulate the sensitivity to the summed regulatory input. Finally, the ANN method defines the degradation of a gene product on the basis of standard mass action kinetics.

Formally, the ANN method is defined as

(8.1)

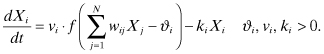
The parameters of the ANN method have the following biological interpretations:

In the ANN method, the parameters w_ij can be intuitively used to define activation and inhibition by assigning positive or negative values, respectively. Here, small absolute values indicate a minor impact on the transcription process (or a missing regulatory interaction), and large absolute values indicate a correspondingly major impact on the transcription process. However, one should be aware that the multiple regulatory inputs required in the case of coregulation can compensate each other due to their additive input processing.

8.2.1.3 TheS-System (SS) Method

Savageau (1976) proposed the synergistic system or SS as a molecular network model. Modeling GRNs with the SS, the expression rates are described by the difference of two products of power law functions, where the first represents the activation term and the second the degradation term of a gene product X_i. This multiplicative input processing can be used to define logical conjunctions for both the regulation of gene expression processes and for the regulation of degradation processes. The SS method has no restrictions in the gene expression rates and thus does not implicitly describe saturation.

Formally, the SS method is defined as

(8.2)

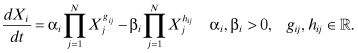
The parameters of the SS method have the following biological interpretations:

The behavior of SS models is mainly determined by the exponent values g_ij and h_ij. Similar to the ANN method, high absolute values define strong influence, whereas small absolute values indicate weak influence. However, the dynamics can become particularly complicated when describing inhibiting dependencies using negative exponent values. Here, the effect depends strongly on the actual concentration ranges of the inhibitor, which can introduce singular behavior at near-zero concentrations.

The parameters used in SS models have a clear physical meaning and can be measured experimentally (Hlavacek and Savageau, 1996), yet they describe phenomenological influences, as opposed to stoichiometric rate constants in general mass action (GMA) systems (Crampin et al., 2004). The SS method generalizes mass action kinetics by aggregating all individual processes into a single activation and a single degradation term (per gene). In contrast, the GMA system defines all individual processes k with k = 1, … , R with the sum of power law functions (Almeida and Voit, 2003).

8.2.1.4 The General Rate Law of Transcription (GRLOT) Method

The GRLOT method has been used to generate benchmark time-series data sets to facilitate the evaluation of different reverse-engineering approaches (Mendes et al., 2003; Wildenhain and Crampin, 2006). GRLOT models multiply individual regulatory inputs. Activation and inhibition are represented by different functional expressions that are similar to Hill kinetics, which allow the inclusion of cooperative binding events (Mendes et al., 2003). Identical to the ANN, the degradation of gene products is defined via mass action kinetics.

Formally, the GRLOT method is defined as

(8.3)

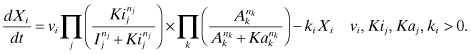
The parameters of the GRLOT method have the following biological interpretations:

The GRLOT method uses two inverse functional forms to describe activating and inhibiting influences, both of which involve two parameters. For example, in the case of activation, each individual dependency is described with a Hill equation where the Hill exponent n_ij determines the sigmoid response curve to varying concentration levels of the regulating molecule. Furthermore, the second parameter, Ka_k, allows the concentration of the regulator molecule to be specified, which gives half of its maximal effect on the expression rate. Consequently, high exponent values, together with low Ka_k values, defined for a regulator molecule, indicate that already low concentration levels have a strong activating effect on the transcription process, while, on the other hand, low exponent values in combination with high Ka_k values require high concentration levels of the regulator molecule for effective activation.

Having discussed the mathematical approaches for modeling GRNs, we now outline the computational techniques we developed for reverse engineering these models.

8.2.2 QCG-OMPI

QCG-OMPI (Coti et al., 2008) is an MPI implementation targeted to computational grids, based on OpenMPI (Gabriel et al., 2004) and relying on a set of grid services that provide advanced connectivity techniques. Although QCG-OMPI can be used as a stand-alone component (and this is how we used it for the application presented in this chapter), it is also a key component of the QosCosGrid (QCG) middleware for which it was designed (Kurowski et al., 2009; Bar et al., 2010).

QCG-OMPI is designed to be topology aware. It supports groups of processors that communicate to each other according to different connective topologies. A novel and important feature of QCG-OMPI is that an application is able to adapt to different application topologies according to the set of resources supplied at run time. Also, any number of communication layers can be defined. The user has complete flexibility and control in terms of the number of communicators and different grains of parallelism.

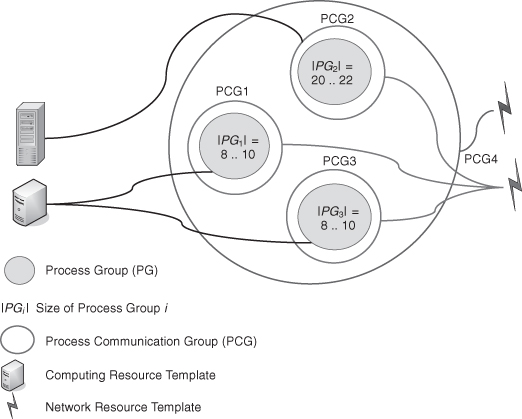
The number of groups a process belongs to is called its depth and is stored under QCG_TOPOLOGY_DEPTH. The groups defined by the user are called colors, and this name is stored under the attribute name QCG_TOPOLOGY_COLORS. QCG-OMPI provides a QCG_ColorToInt() function to convert alphanumeric colors into integers that can be passed to the MPI_Comm_split() routine in order to create communicators that fit the topology.

Figure 8.2 depicts an example application based on the evolutionary algorithm software we have used in this chapter. It defines four communication groups or process groups (PG): PG1, PG2, PG3, and PG4. PG4 includes all the processors, while PG1, PG2, and PG3 comprise mutually exclusive subsets. When QCG-OMPI is deployed as a stand-alone component, the details of the process groups may be passed to the application via the environmental variables QCG_TOPOLOGY_DEPTHS and QCG_TOPOLOGY_COLORS. The application can obtain this topology information at any moment during execution, that is, after the MPI library has been initialized and before its finalization.

Figure 8.2 A sample request representation of a topology-aware evolutionary algorithm application.

Additional functionality is available if QCG-OMPI is deployed on the full QCG multiuser infrastructure. In this case, users specify the technical capabilities required for the different process groups, including the properties of the network connecting the different groups. In the QCG, each process group is mapped to a computing resource template that describes the properties of the machines it requires for correct execution. A computing resource template is an instantiation of an XML schema describing the properties of computing resources. To enable a flexible approach to scheduling, and to take advantage of the ability of topology-aware QCG-OMPI applications to adapt to available resources, the computing resource template is described in terms of ranges. For example, the computing resource template requested by both PG1 and PG3 might be specified as follows:

These requirements are then passed to the QosCosGrid Scheduler through the environmental variable QCG_TOPOLOGY_DEPTHS.

When used on the QCG infrastructure, process groups are arranged in a process communication group (PCG) topology, where it is assumed that all processes within a PCG would like to have all-to-all interconnections with certain properties. The quantitative properties of these interconnections are specified by means of the network resource templates (a network resource template is an instantiation of an XML schema describing possible network properties).

For instance, PCG1 (one of the small inner circles) contains only processes of PG1, which means that all the processes of PG1 must have all-to-all interconnections as described in the PCG1’s network resource template. On the other hand, PCG4 (the large outer circle) contains three process groups—PG1, PG2, and PG3, which means that all the processes of these three process groups must have all-to-all interconnections as described in the PCG4’s network resource template. Given any two processes, we can determine the quality of their interconnection by looking into the smallest circle (PCG) that contains these two processes. The network templates are used by the QosCosGrid Scheduler, along with the computing resource templates, when allocating network and computing resources for an application.

An example of the topology depicted in Figure 8.2 is given in Table 8.1. This is valid whether QCG-OMPI is used as a stand-alone component or on the QCG infrastructure. In this example, each process group contains two processes. The application’s processes, at run time, can obtain the topology description (represented by Table 8.1) by obtaining the appropriate MPI attributes from the run-time environment. For example, the MPI code to fetch these attributes from the run-time environment is

/* depths is an array of integers of size NPROCS */

MPI_Attr_get(MPI_COMM_WORLD, QCG_TOPOLOGY_DEPTHS, depths, &flag);

TABLE 8.1 Array of Colors Corresponding to the Topology Depicted in Figure 8.2

Instructions within the program inform processes what they have to do, regarding their color at a given depth, and what computation pattern they should adopt. Processes can also use colors to adapt their communication patterns. In particular, they can build communicators that fit the requested communication groups using the MPI routine MPI_Comm_split().

The color used by MPI_Comm_split () is the integer translation of the QCG alphanumeric color, given by the QCG_ColorToInt() routine. Processes that do not belong to any communication group at a given depth are assigned the MPI_UNDEFINED color and create an invalid communicator, as specified by the MPI standard.

QCG-OMPI presents the topology to the application as an array containing (for each process indexed by its rank in the global communicator MPI_COMM_WORLD) strings that represent the names of communication groups. Thus, each process in the system is able to determine to which groups it belongs in a very simple way. QCG-OMPI also provides a conversion function to create a unique identifier per communication group name, suitable to be used for the MPI_Comm_split() function of the MPI standard, enabling a simple creation of individual communicators per communication group. Using these topology-aware process groups, populations can evolve within each process group and communicate using local communicators, and use the global MPI_COMM_WORLD communicator or other user-defined communicators, for cross-group communications only.

The communication middleware of QCG-OMPI takes care of establishing the communication links on demand. This happens transparently for the application developer, even if the peers of the communication are located in different clusters, separated by firewalls, or if the communication involves many peers in many different locations (e.g., when doing a collective operation on a communication group instantiated as a communicator spanning multiple sites). Thus, programming parallel applications in QCG-OMPI remains natural for MPI users, and it becomes simple to discover which resources have been allocated to which communication group (an addition to the MPI standard proposed by QCG-OMPI).

8.2.3 A Topology-Aware Evolutionary Algorithm

Evolutionary algorithms are an approach inspired by biological evolution to iteratively evolve and optimize, according to some criteria, a population of computing objects, where each individual in the population is a potential solution to the problem at hand (Holland, 1992; Bäck, 1996). The individuals of an evolutionary algorithm may be organized around specific population structures or topologies. We distinguish two approaches: island evolutionary algorithms and cellular evolutionary algorithms.

PSO is a population-based stochastic optimization technique that shares many similarities with other evolutionary computation techniques (Kennedy and Eberhart, 1995). An appealing feature of PSO is that it requires relatively few parameters when compared to evolutionary algorithms, such as genetic algorithms, that use transformations such as mutation, crossover, and so on, to generate solutions. It is this simplicity that encouraged us to apply it to reverse-engineering GRNs.

In PSO, the population of potential solutions consists of particles that “fly” through the problem space by following a trajectory that is influenced by the current optimal solution, the particle’s own best solution, and, in our implementation, the optimal solution of its immediate neighbors.

As with other evolutionary algorithms, PSO is initialized with a group of random solutions and then searches for optima by updating generations. The generations are updated at every iteration by using Equation 8.4 to calculate the particles’ current velocities:

(8.4)

(8.5)

Here R₁, R₂, and R₃ are random numbers between 0 and 1, and the constants c₁, c₂, and c₃ represent learning factors that in PSO algorithms are usually set to 2. The optimal or best current solution or fitness that particle i has achieved is denoted by and the optimal or best current solution of its local neighbors is denoted by l^best. Finally, the optimal or best current value obtained by any particle in the subpopulation is given by g^best. Periodically, using the message passing functions implemented by QCG-OMPI, the particles communicate their current optimal or best solutions, , with the rest of the population and receive values for l^best and g^best.

The PSO algorithm is one of a number of evolutionary algorithms that we implemented in a program called CellXPP. CellXPP is written in C, and while the QCG-OMPI routines are handled by the C program, the fitness function uses a Python interface to call XPPAUT,¹ a program maintained by G. Bard Ermentrout to solve the differential equations. We used XPPAUT because it is a well-established piece of software with a large user community and, more importantly, because it provides a command-line interface and is easy to install on a variety of different machine architectures. The Python interface was used to convert the current parameter set of a particle into an execution file (with the correct set of differential equations for XPPAUT) and then process the output of XPPAUT using Equation 8.6 to calculate a fitness value. Python was used because of its scripting capabilities that allowed us to quickly experiment with new sets of differential equations and different approaches to calculate the fitness.

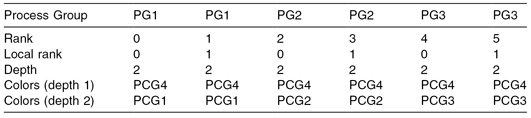
The application consists of two layers or PCGs that combine features of both cellular and (cooperative) island evolutionary algorithms, thus giving the application a two-layer topology. In this setup, the algorithm is aware of the two layers; hence, we call it a topology-aware evolutionary algorithm. More frequent communications, at every iteration, take place in the lower layer (cellular aspect of the combined evolutionary algorithm approach), and less frequent communications, perhaps every 100 iterations, take place in the higher layer (insular aspect). These are shown in Figure 8.3 with a ring topology used for communications between island subpopulations, while in the cellular layer, individuals communicate with their immediate neighbors.

Figure 8.3 Communication topology of the PSO algorithm. The arrows show the communication patterns in each process communication group: Communications in the island layer can be mapped onto a ring topology, while communications in the cellular layer can be mapped onto a spherical topology where each process communicates to its neighbors.

In Figure 8.3, the evolutionary algorithm is composed of three subpopulations, which may be distributed over any number of physical locations. However, in general, the algorithm can divide the population into one or more subpopulations. A subpopulation may run over multiple physical locations, and it is also possible for multiple subpopulations to run at a single physical location. The exact distribution of the population is left to the user to decide and may be specified at run time. The topology-aware functionality of QCG-OMPI is then able to adapt the application to the specified communication topology. Normally, due to the relatively frequent communication patterns taking place within subpopulations, subpopulations are most efficiently executed on one computational cluster at a single physical location.

Time-series gene expression data form the input to our reverse-engineering process. We aim to identify model parameters for which the discrepancy between the experimental data and the data predicted by the model is minimal (Wessels et al., 2001). This leads to an optimization problem in which the following function is to be minimized:

(8.6)

where X_k(t) denotes the experimentally observed gene product concentration level of gene k at time point t; denotes the gene product concentration level of gene k at time point t predicted by the dynamic GRN model; N denotes the number of genes in the network; and T represents the number of sampling points of observed data.

The parameter space searched for the three mathematical methods described in Section 8.2.1 was defined as follows:

• ANN Method: w_ij from −15.0 to 15.0, v_i from 0.0 to 3.0, ϑ_i from 0.0 to 7.0, and k_i from 0.0 to 2.0
• SS Method: g_ij and h_ij from −3.0 to 3.0, and α_i and β_i from 0.0 to 15.0
• GRLOT Method: I_j, from −5.0 to 5.0, A_k from 0.0 to 7.0, Ki_j and Ka_k from 0.0 to 40.0, and k_i from 0.0 to 2.0

The topology awareness of the evolutionary algorithm could be extended to include a third topology layer that would be used if the fitness calculation had to be parallelized. For example, if the machines allocated have multiple cores or multiple processors, then one way of implementing the third topology layer involves placing all available processes from a machine into a group. The topology-aware algorithm would then be able to adapt to each machine, depending on the number of cores and processors that it possesses. The three layers of the topology-aware algorithm would then include parallelization at the machine level, parallelization at the cluster level, and parallelization at the cross-cluster or grid level.

8.3 RESULTS AND DISCUSSION

First, we discuss some performance characteristics of the GRN reverse-engineering application in terms of its computational efficiency and ability to scale over distributed resources, then we show the results of our reverse-engineering experiments with the Cantone et al. (2009) yeast regulatory network and the three mathematical methods.

8.3.1 Scaling and Speedup of the Topology-Aware Evolutionary Algorithm

Using the topology-aware evolutionary algorithm described in Section 8.2.3, we have conducted a number of computational studies on Grid’5000, which is an academic, nationwide experimental grid dedicated to research (Cappello et al., 2005). In these studies, we used QCG-OMPI as a stand-alone component, without any other features of the QCG middleware. For the experiments we performed, we were allocated resources for which we were the only user.

We used two sites, located in the cities of Orsay and Bordeaux in France. These locations are physically separated by several hundred kilometers. The specifications of the clusters are as follows:

• In Orsay, a cluster called GDX was used. It is based on AMD Opteron machines with two single-core CPUs running at 2.4 GHz and with 2.0-GB memory. For the Orsay cluster experiments, we had 120 cores available in 60 machines.
• In Bordeaux, a cluster called Bordereau was used. It is based on AMD Opteron machines with dual-processor dual-core CPUs running at 2.6 GHz and 4.0-GB memory. For the Bordeaux cluster experiments, we had 120 cores available in 30 machines.

The nodes within each cluster were interconnected by a Gigabit Ethernet switch, and the clusters were connected by the Renater French Education and Research Network using a 10-Gb/s dark fiber.

The evolutionary algorithm performs one fitness calculation per CPU core. If the algorithm is scaling well, as the number of cores increases, we would hope to see the time required to perform a fitness calculation to remain constant—so, 200 cores perform 200 fitness calculations in the same time as 40 cores perform 40 fitness calculations.

Figure 8.4 depicts the results of the five experiments using the two Grid’5000 clusters. It shows the speedup of the evolutionary algorithm execution and depicts the average time to execute an iteration of the evolutionary algorithm when running on different clusters with different topologies. At each iteration, an individual (or a process running on a different CPU core) performs a fitness calculation and communicates the results to its neighboring processes. As the number of cores increases, so does the size of the population, which results in an increase in the number of fitness calculations performed at each iteration.

Figure 8.4 Speedup results of the evolutionary algorithm using different clusters and computational resources. Note that the number of cores corresponds to the population size and hence the number of fitness calculations performed in an iteration. The graphs are discussed in the main text.

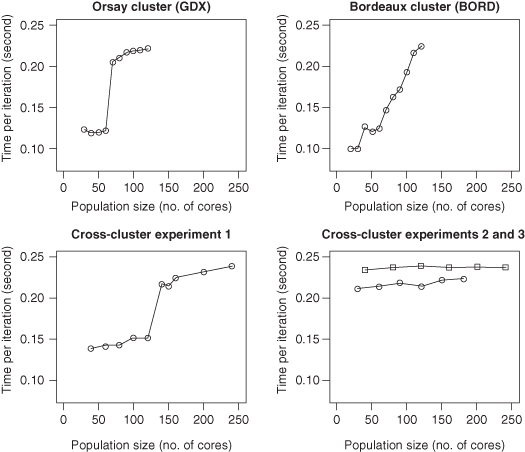
In Figure 8.4, the graphs labeled “GDX” and “BORD” depict execution times of runs performed on a single cluster, corresponding to the Orsay cluster (GDX) and the Bordeaux cluster (BORD), respectively. The other two graphs (labeled “Cross-cluster experiment 1,” “Cross-cluster experiment 2,” and “Cross-cluster experiment 3,” respectively) show three cross-cluster runs performed on both clusters (GDX and BORD).

For the GDX simulations, we initially ran just 1 process per machine, up to 60 processes; then, we used both CPUs on each machine, up to the full number of 120 CPUs. There is a noticeable increase in execution time at the transition from one to two CPUs per machine. Up to 60 CPUs, the speedup is linear, and above 60 CPUs, the speedup is also approximately linear but with a greater time required to perform a full iteration.

For the BORD simulations, we initially restricted processes to run on just 1 core per machine (30 cores in total). Then, we increased this to 2 (from 30 to 60 cores), then to 3 (from 60 to 90 cores), and finally, we used all 4 cores available in each machine. Here, we observed a sudden increase in execution time at the transition from one to two cores per machine—here, the two cores are on separate CPUs within the same machine. However, when progressing from two to three or four cores, the execution time increases according to the number of cores used—in this case, the speedup is not linear. When we increased the number of processes per machine, we kept the number of network interface cards constant. We speculate that there is congestion at the level of network interface cards because several processes are trying to communicate through the network using a single network interface card. Thus, the communication time within a machine is greater when running several processes per machine.

For Cross-cluster experiment 1, we performed a cross-cluster run by trying to minimize the number of processes run on each machine. This experiment follows a similar pattern to the runs on GDX and BORD: Initially, one process is run on a machine using one CPU on each machine on GDX and one CPU on BORD (from 30 to 90 cores). Next, we used two BORD CPUs (from 90 to 120 cores) followed by both the CPUs for the GDX machines (from 140 to 160 cores). And for the final two points where population size (number of cores) is changed from 210 to 240 cores, we used all the available cores in the machines. The shape of the graph is similar to that of the individual runs, particularly the GDX run with its sudden increase in execution time when both CPUs are used in each machine. Overall, the execution times are slightly longer when running across both clusters; this may be due to the increased communication overhead between the different physical locations.

For the Cross-cluster experiments 2 and 3, we used the maximum available cores and/or CPUs in each machine; that is, for Cross-cluster experiment 2, we used all the available cores per machine on GDX and two cores per machine on BORD (this is the lower line in the figure); and for Cross-cluster experiment 3, we ran two processes per machine on GDX and four processes per machine on BORD (this is the top curve in the bottom-right graph in Fig. 8.4). These simulations show that the speedup is approximately linear. Since the speedup is linear, this means that the communication pattern is scalable; that is, there is no bottleneck. This implies that our cellular communication pattern is a good architecture for this infrastructure, and that it does not suffer from congestion, which might be a problem for more common parallelization schemes based on master–worker communication patterns.

It is clear for this application that the cross-cluster communications (hundreds of kilometer distance between Orsay and Bordeaux) are not a limiting factor. Instead, the main limitation arises from the use of Python scripts to interface with the XPPAUT software through system calls. This is due to the relatively inefficient operations caused by running multiple processes on the individual machines—when several processes are running on the same machine, a situation of concurrency between processes on disk accesses can be created. This hinders the sequential parts of the parallel algorithm and thus increases the total execution time.

8.3.2 Reverse-Engineering Results

The 10 graphs in Figures 8.5 and 8.6 show the gene expression data of the five genes in the Cantone network, CBF1, GAL4, SWI5, GAL80, and ASH1, along with the dynamics predicted by the three methods. The error bars shown are for the experimentally derived data of Cantone et al. (2009). The ANN and GRLOT methods tend to provide a good match to the experimental data, with the ANN method giving the best results in this test. The predictions made by the SS method are clearly worse than the other two methods.

Figure 8.5 Reverse-engineering results for switch-on data from Cantone et al. (2009). In the graphs, the points with error bars depict experimental data and the lines represent the models.

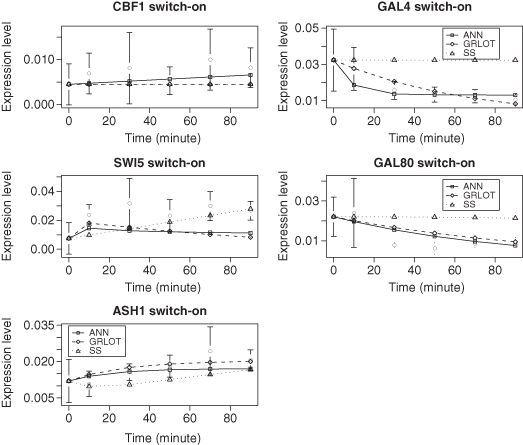
Figure 8.6 Reverse-engineering results for switch-off data from Cantone et al. (2009). In the graphs, the points with error bars depict experimental data, and the lines represent the models.

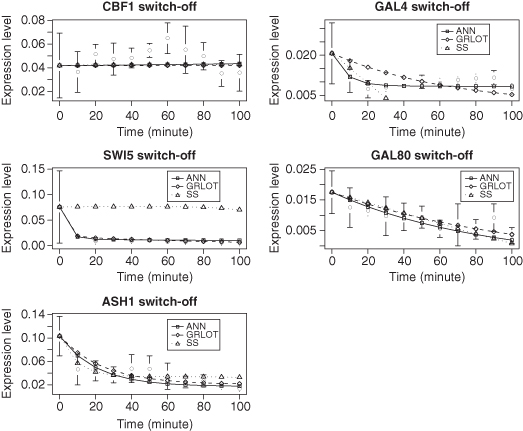
The SS method couples unrestricted expression rates with input processing based on multiplied exponentials, which, in the experiments we have explored in this chapter, frequently leads to extreme sensitivity and unstable dynamics. Indeed, it is common that the parameter values automatically generated by the evolutionary algorithm for the SS method do not give any solution. This is because extremely large exponential terms in the equations lead the integrator to quickly fail. As a result, the evolutionary algorithm tends toward solutions where the influence of the power terms is minimized by setting the values of their parameters to values close to zero, giving linear graphs. However, as genes may be close to a steady state of expression for much of the time series, a linear solution may be a reasonably accurate solution and thus does not significantly impact on the overall model output.

The three methods are designed to be flexible enough to find phenomenological expressions for their approximations of experimentally observed behavior (Vohradsky, 2001; Crampin et al., 2004). In contrast to GRN models based on the SS and GRLOT methods, where regulatory inputs are exponentiated and multiplied, GRN models based on the ANN method weight and sum multiple regulatory inputs. An attraction of the SS and GRLOT methods is that their input processing accords better than that of the ANN method with the fundamentals of reaction kinetics and collision theory (chemical reaction rates correlate with the multiplied concentrations of the reactants). However, none of the three methods follow strictly the chemical reaction processes because a single kinetic equation typically comprises several processes. An advantage of the ANN method is that its approach of weighting and summing regulatory inputs is relatively robust and avoids the extreme sensitivity of the SS method. For example, when the evolutionary algorithm randomly selects parameters for the ANN method, they almost always lead to solvable equations. Of the three methods, it is our experience that the ANN method tends to require relatively less computation to achieve an accurate solution and is therefore to be preferred over the GRLOT and SS methods. A more detailed comparison of the three methods is given in Swain et al. (2010).

8.4 CONCLUSIONS

QCG-OMPI is an effective and efficient framework for distributed evolutionary algorithms. The topology awareness of QCG-OMPI simplifies the software development process for the evolutionary algorithm, and, although the programmer must define the functionality of the communication groups within the code, there is no need to define the number or size of the groups as these are allocated automatically at run time.

Distributed evolutionary algorithms often combine a number of different topologies, such as the master–worker topology or the topologies we have explored in this chapter. QCG-OMPI makes it easy to define different communication groups in a flexible way so that an evolutionary algorithm can automatically adapt to different collections of computing resources. As a result, programmers can exploit distributed resources and parallel topologies to develop novel approaches to reverse-engineering GRNs. For example, different island populations might use different mathematical methods in order to overcome the biases and weaknesses of generating models with just a single method. While complete sets of parameters are not transferable between different systems of equations, there are useful results that may be transferred. For instance, if the topology of the network is unknown, then one task of the reverse-engineering process involves predicting which genes are not interacting with each other, which is modeled by putting the weights w_i,j to zero in the ANN method, or the exponents n_i,j to zero in the GRLOT method. Results such as these are easily transferable between the mathematical methods.

Even for very small gene networks, considerable amounts of highly time-resolved data, with many sampling points based on multiple perturbations and experimental conditions, may be necessary to produce reliable dynamic GRN models. Our studies suggest that mathematical methods used to model GRNs are not equivalent, and because of considerable differences in the way the methods process inputs, the models they create may vary considerably in terms of accuracy. Furthermore, as the complexity in terms of the number of genes and regulatory interactions increases, the computational complexity and computing power required to reverse engineer dynamic GRN models becomes nontrivial, requiring nonstandard computing solutions such as clusters, supercomputers, or other large-scale computing solutions. QCG-OMPI and the software discussed in this chapter are an attractive solution to meet these challenges.

ACKNOWLEDGMENTS

The work reported in this chapter was supported by EC grants DataMiningGrid IST FP6 004475, QCG IST FP6 STREP 033883, and ICT FP7 MAPPER RI-261507. Some of the presented experiments were carried out using the Grid’5000 experimental test bed, being developed under the INRIA ALADDIN development action with support from the Centre National de la Recherche Scientifique (CNRS), Reseau National de Télécommunication pour la Technologie, l’Enseignement et la Recherche (RENATER), and several universities as well as other funding bodies (see https://www.grid5000.fr).

Note

1 http://www.math.pitt.edu/∼bard/xpp/xpp.html.

REFERENCES

J. S. Almeida and E. O. Voit. Neural-network-based parameter estimation in S-system models of biological networks. Genome Informatics, 14:114–123, 2003.

T. Bäck. Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms. Oxford, UK: Oxford University Press, 1996.

P. Bar, C. Coti, D. Groen, et al. Running parallel applications with topology-aware grid middleware. In Fifth IEEE Int’l Conference on eScience, Oxford, UK, December 9–11, 2009, pp. 292–299, 2010.

I. Cantone, L. Marucci, F. Iorio, et al. A yeast synthetic network for in vivo assessment of reverse-engineering and modeling approaches. Cell, 137(1):172–181, 2009.

F. Cappello, E. Caron, M. Dayde, et al. Grid’5000: A large scale and highly reconfigurable grid experimental testbed. In Proc. of the 6th IEEE/ACM Int’l Workshop on Grid Computing (SC’05), pp. 99–106, Seattle, WA: IEEE/ACM, 2005.

C. Coti, T. Herault, S. Peyronnet, et al. Grid services for MPI. In 8th Int’l Symposium on Cluster Computing and the Grid (CCGRID’08), pp. 417–424, Washington, DC: IEEE Computer Society, 2008.

E. J. Crampin, S. Schnell, and P. E. McSharry. Mathematical and computational techniques to deduce complex biochemical reaction mechanisms. Progress in Biophysics and Molecular Biology, 86(1):77–112, 2004.

E. Davidson and M. Levin. Gene regulatory networks. Proceedings of the National Academy of Sciences of the United States of America, 102(14):4935–4935, 2005.

E. Gabriel, G. E. Fagg, G. Bosilca, et al. Open MPI: Goals, concept, and design of a next generation MPI implementation. In Proc. of the 11th European PVM/MPI Users’ Group Meeting, pp. 97–104, Budapest, Hungary, September 2004.

M. Gorges-Schleuter. Asparagos an asynchronous parallel genetic optimization strategy. In Proc. of the 3rd Int’l Conference on Genetic Algorithms, pp. 422–427, San Francisco, CA: Morgan Kaufmann Publishers Inc., 1989.

J. Hasty, D. McMillen, F. Isaacs, et al. Computational studies of gene regulatory networks: In numero molecular biology. Nature Reviews Genetics, 2(4):268–279, 2001.

W. S. Hlavacek and M. A. Savageau. Rules for coupled expression of regulator and effector genes in inducible circuits. Journal of Molecular Biology, 255(1):121–139, 1996.

J. H. Holland. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence. Cambridge, MA: MIT Press, 1992.

J. Kennedy and R. Eberhart. Particle swarm optimization. In Proc. of the IEEE Int’l Conference on Neural Networks. IV, pp. 1942–1948, 1995.

K. Kurowski, W. Back, W. Dubitzky, et al. Complex system simulations with QosCosGrid. In K. Kurowski et al., editors, ICCS ’09: Proc. of the 9th Int’l Conference on Computational Science, pp. 387–396, Berlin: Springer-Verlag, 2009.

P. Mendes, W. Sha, and K. Ye. Artificial gene networks for objective comparison of analysis algorithms. Bioinformatics, 19(90002):122–129, 2003.

M. A. Savageau. Biochemical Systems Analysis: A Study of Function and Design in Molecular Biology. Reading, MA: Addison-Wesley, 1976.

M. T. Swain, J. J. Mandel, and W. Dubitzky. Comparative study of three commonly used continuous deterministic methods for modeling gene regulation networks. BMC Bioinformatics, 11(459):1471–2105, 2010.

J. Vohradsky. Neural network model of gene expression. The FASEB Journal: Official Publication of the Federation of American Societies for Experimental Biology, 15(3):846–854, 2001.

L. Wessels, E. van Someren, and M. Reinders. A comparison of genetic network models. In Proc. of the Pacific Symposium on Biocomputing, pp. 508–519, 2001.

J. Wildenhain and E. J. Crampin. Reconstructing gene regulatory networks: From random to scale-free connectivity. IEE Proceedings of Systems Biology, 156(4):247–256, 2006.