2
Probability Theory
The reason why many wireless communication books start from probability theory is that wireless communications deal with uncertainty. If there are no channel impairments by nature, we can receive the transmitted messages without any distortion and don’t need to care about probability theory. However, nature distorts and interferes when electromagnetic waves propagate. In wireless communication systems, the received messages over a wireless channel include many channel impairments such as thermal noises, interferences, frequency and timing offsets, fading, and shadowing. Thus, wireless communication systems should overcome these impairments.
2.1 Random Signals
Wireless communication systems are designed to deliver a message over a wireless channel. It is assumed that the transmitted messages include a random source and the received messages cannot be predicted with certainty. In addition, wireless channel impairments including thermal noises are expressed as random factors. Therefore, we need to know mathematical expression and characteristics of random signals.
We can divide signals into deterministic signals and non-deterministic signals. The deterministic signals are predictable for arbitrary time. It is possible to reproduce identical signals. The deterministic signals can be expressed by a simple mathematical equation and each value of the deterministic signal can be fixed as shown in Figure 2.1. We know each value with certainty at any time through mathematical calculation.

Figure 2.1 Example of a deterministic signal
On the other hand, non-deterministic signals are either random signals or irregular signals. The random signals cannot be expressed by a simple mathematical equation and each value of the random signal cannot be predicted with certainty as shown in Figure 2.2.

Figure 2.2 Example of a random signal
Therefore, we use probability to express and analyze a random signal. The irregular signals are not describable by probability theory. It occasionally occurs in wireless communications. The statistic metrics such as average and variance are useful tool to understand random signals. Now, we look into not one random signal but a collection or ensemble of random signals and define useful terms. A random variable is useful to express unpredictable values. It is defined as follows:
There are two types of random variables: discrete random variable when X has discrete values and continuous random variable when X has continuous values. The probability distribution (or probability function) of a random variable is probabilities corresponding to each possible random value. If we deal with continuous random variables, it is difficult to express the probabilities of all possible events. Thus, we define the Probability Density Function (PDF) which is the probability distribution of a continuous random variable. The probability distribution, P(X), of the discrete random variable, X = xi, is defined as follows:
where X takes n values and the probability, pi, has the following properties:
where ![]() and
and ![]() .
.
The Cumulative Distribution Function (CDF) (or distribution function), FX(xi), of the discrete random variable, X, is defined as follows:
This means the probability that the random variable, X, is less than or equal to xi. When the random variable, X, has interval (xa, xb], the probability distribution and the cumulative distribution function can be represented as follows:
where the notation ( ] denotes a semi-closed interval and ![]() . The properties of the distribution function are as follows:
. The properties of the distribution function are as follows:
We will meet those two important functions when dealing with wireless communication systems. The most important probability distribution in wireless communications is Gaussian (or Normal) distribution. It is defined as follows:
where σ and μ are standard deviation and mean of the distribution, respectively. The cumulative distribution function of Gaussian distribution is as follows:
where error function, erf( ), is defined as follows:

Wireless communication systems basically overcome many types of channel impairments. Thus, we must describe and analyze the noise mathematically and the natural noise such as thermal noises is expressed by Gaussian distribution.
When a system is composed of a sample signal ![]() and a collection of time function
and a collection of time function ![]() , we define a random process as follows:
, we define a random process as follows:
A random signal cannot be predicted but we may forecast future values from previous events using probability theory. Thus, we can deal with wireless channel impairments and distorted signals (thermal noise, nonlinear distortion of electronic devices, etc.) randomly but not irregularly. The random process is very useful model to describe an information source, transmission, and noise. When we consider a random noise generator, its waveforms are as shown in Figure 2.5.

Figure 2.5 Random noise generator
The random noise generator creates n waveforms. Each sample signal, si, for a specific time (t1) is a random variable. When we observe only random variable, si, the probability distribution is expressed as follows:
and

When we observe one sample signal, s1, we can have a sample time function, X(t). The random process, X(s, t), becomes a real number, X(s1, t1), when we fix a specific sample signal (s1) and time (t1).
2.2 Spectral Density
An electromagnetic wave transmits information and transfers a power in the air. When we analyze the distribution of the signal strength in frequency domain, the spectral density of the electromagnetic wave is very useful concept. When we consider a signal over time, s(t), we find the Energy Spectral Density (ESD) and Power Spectral Density (PSD). If s(t) is a voltage across a resistor, R, to be 1 Ω, the instantaneous power, p(t), is as follows:

and the total energy, Es, of s(t) is as follows:

where S(ω) is the Fourier transform of s(t), ω is the angular frequency ![]() , and f is the ordinary frequency. We can obtain this relationship between time domain energy and frequency domain energy from Parseval’s theorem [1]. The energy spectral density of the signal can be found as follows:
, and f is the ordinary frequency. We can obtain this relationship between time domain energy and frequency domain energy from Parseval’s theorem [1]. The energy spectral density of the signal can be found as follows:

where E(f ) denotes the squared magnitude and energy spectral density of the signal s(t). It means the signal energy per unit bandwidth and its dimension is joule per hertz. Basically, the energy is infinite but the power is finite. Therefore, the power spectral density is more useful to describe a periodic signal. We define an average power, Ps, as follows:




where P( f ) is the power spectral density of the periodic signal s(t). It means the signal power per unit bandwidth and its dimension is watts per hertz. If we have a non-periodic signal, we can observe a certain time interval of the signal and have its power spectral density.

Figure 2.6 Periodic signal, s(t)
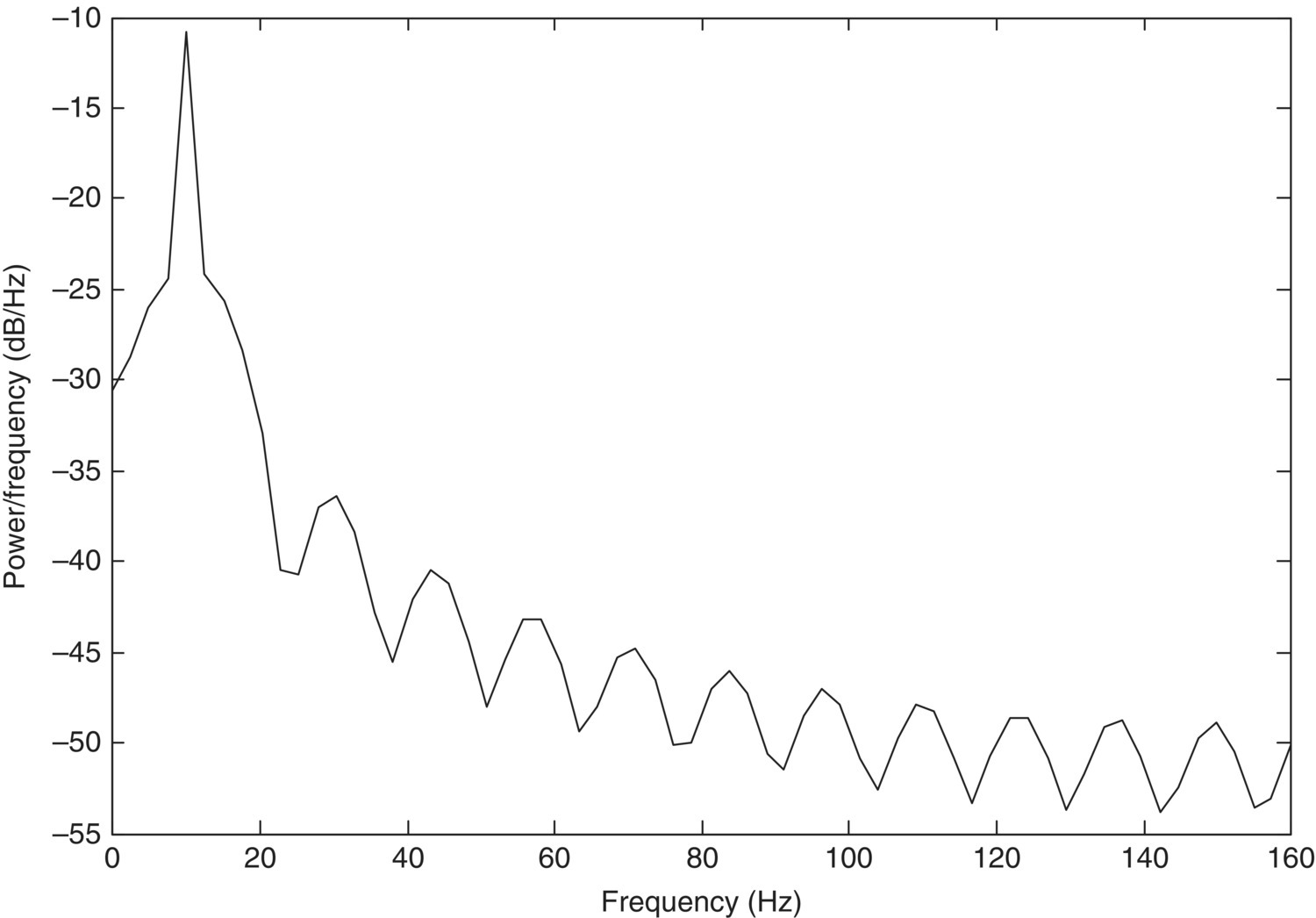
Figure 2.7 Power spectral density of the periodic signal, s(t)
2.3 Correlation Functions
A correlation function is used to know the relationship between random variables. In wireless communication systems, synchronization blocks are based on this correlation function. In a random process, we assume to deal with a whole signal. However, we may sometime have a part of the signal and need to describe it. In this case, we can derive some parameter from the ensemble. If we obtain an average from this ensemble, we call this ensemble average. When a discrete random variable, X, has values, xi, and probabilities, pi, where ![]() , the expectation (or mean function) of this random variable is as follows:
, the expectation (or mean function) of this random variable is as follows:
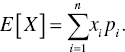
For a continuous random process, we define it as follows:
An autocorrelation is used to measure a similarity of signals and means how much a signal matches with a time lag version. We define the autocorrelation function using expectation and Figure 2.8 shows us its visual description.

Figure 2.8 Example of an autocorrelation
When a random process is not varying with the time origin and all statistic parameters are not affected, we call it strict sense stationary process. If two statistic parameters, expectation and variance, are not varying with respect to time shift, we call it wide sense stationary process. For a wide sense stationary process, we express expectation and autocorrelation function as follows:
and
This equation means that the autocorrelation depends on the time difference ![]() . Now, we express the autocorrelation as follows:
. Now, we express the autocorrelation as follows:


where the operation “*” represents the complex conjugate.
When we need to know a similarity of two different random processes, cross-correlation is useful and measures a similarity between a transmitted signal and a stored signal in the receiver. The cross-correlation function is defined as follows:
The visual description of cross-correlation is shown in Figure 2.9.

Figure 2.9 Example of a cross-correlation
A matched filter based on the cross correlation function is very useful for detecting a known signal from a signal that has been contaminated by wireless impairments. The input, x(t), of the matched filer can be expressed as follows:
where s(t), A, td, and n(t) are a known transmitted signal, an unknown scaling factor, an unknown time delay, and additive noise, respectively. The output, y(t), of the matched filter is expressed as follows:
where h(t) and the operation “![]() ” denote a matched filter and convolution, respectively. The system model of the matched filter is illustrated in Figure 2.10.
” denote a matched filter and convolution, respectively. The system model of the matched filter is illustrated in Figure 2.10.
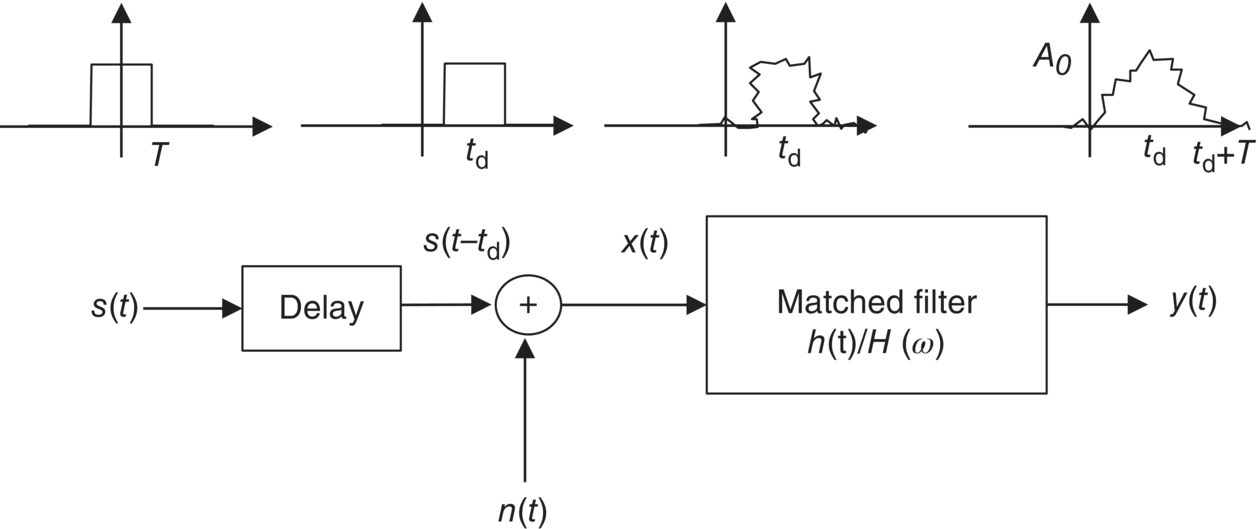
Figure 2.10 Matched filter system model
Basically, the matched filter is a linear filter and has a sharp peak output. We know information of the transmitted signal by a time (td + T ) and amplitude (A0) of the matched filter output. The impulse response of the matched filter with additive white noise is
We represent the matched filter output using autocorrelation function as follows:



where ![]() . If the input, x(t), is perfectly matched, the output of the matched filter is identical to autocorrelation of s(t) as following:
. If the input, x(t), is perfectly matched, the output of the matched filter is identical to autocorrelation of s(t) as following:

Figure 2.11 Transmitted sinc function signal, s(t)

Figure 2.12 Received sinc function signal, r(t)

Figure 2.13 Matched filter output, y(t)
2.4 Central Limit Theorem
When we face a noise that the nature has made electrical component noises or thermal noises, we assume it follows Gaussian distribution because of central limit theorems. In this section, we investigate central limit theorem and its characteristic. The central limit theorem is defined as follows:
This theorem means that the sample average and sum have Gaussian distribution regardless of distribution of each random variable. Now, we can find many examples from our daily life. Example 2.5 shows us that a random number generation converges to normal distribution.


Figure 2.14 Histograms of observed sample sum by n random source generators
A Gaussian distribution with average value, μ, and variance, σ2, is denoted as N(μ, σ2). It has been expressed as (2.11). The standard Gaussian distribution (N(0, 1)) with ![]() and
and ![]() is
is

The cumulative distribution function of the standard Gaussian distribution is

2.5 Problems
- 2.1. Let a random variable, X, and corresponding probabilities, pi, have the following values:
X 1 2 3 4 5 6 7 pi 0.05 0.25 0.15 0.1 0.2 0.15 0.1 Check the properties of random variable and probability distribution.
- 2.2. Let a random variable, X, have the following parameters:
Gaussian 1 Gaussian 2 Gaussian 3 Gaussian 4 Gaussian 5 σ 0.1 0.3 0.7 0.5 0.2 μ 0.2 0.5 −0.8 −0.2 0.1 Plot the Gaussian distribution and its cumulative distribution function.
- 2.3. Consider a non-periodic signal, s(t), and Fourier transform having the following parameters:
Non-periodic signal  where N(t) is a random noise
where N(t) is a random noiseSample frequency 32 Hz Time interval 0–0.32 seconds FFT size 128 Plot the normalized single side power spectral density of the signal, s(t).
- 2.4. Let s(t) be the transmitted signal with a rectangular shape pulse as following:

where

and the received signal, r(t), is
 . Describe the matched filter process.
. Describe the matched filter process. - 2.5. Consider a dice tossing with n dices whose output is from 1 to 6. When we toss 10 000 times with n dices, observe the samples sum (X value) while the number of dice increases.
- 2.6. Consider a coin tossing. The random process, X(t), is defined as follows:

Plot the sample functions and find the PDF of the random variables at t = 1.
- 2.7. Consider
 where A is constant and θ is a random variable uniformly distributed in the range
where A is constant and θ is a random variable uniformly distributed in the range  . Check whether or not the process is wide sense stationary process.
. Check whether or not the process is wide sense stationary process. - 2.8. Show that the cross-correlation of f(t) and g(t) is equivalent to the convolution of f*(−t) and g(t).
- 2.9. Consider a Gaussian noise with the psd of N0/2. Find the autocorrelation function of the output process when a low pass filter with bandwidth B receives Gaussian noise as an input.
- 2.10. The number of phone call per each hour in one base station follows Gaussian distribution with μ = 500 and σ = 300. Suppose that a random sample of 30 hours is selected and the sample mean
 of the incoming phone calls is computed. Describe the distribution of the sample mean
of the incoming phone calls is computed. Describe the distribution of the sample mean  and find the probability that the sample mean
and find the probability that the sample mean  of the incoming phone calls for 30 hours is larger than 650.
of the incoming phone calls for 30 hours is larger than 650. - 2.11. A dice is tossed 50 times. Using the central limit theorem, find that probability that (i) the sum is greater than 250, (ii) the sum is equal to 200, and (iii) the sum is less than 150.
Reference
- [1] S. Haykin, Communication Systems, John Wiley & Sons, Inc., Now York, 1983.


