Preface

This book presents an introduction to fast sequential Monte Carlo (SMC) methods for counting and optimization. It is based mainly on the research work of Reuven Rubinstein and his collaborators, performed over the last ten years, on efficient Monte Carlo methods for estimation of rare-event probabilities, counting problems, and combinatorial optimization. Particular emphasis is placed on cross-entropy, minimum cross-entropy, splitting, and stochastic enumeration methods.

Our aim was to write a book on the SMC methods for a broad audience of engineers, computer scientists, mathematicians, statisticians, and, in general, anyone, theorist or practitioner, interested in efficient simulation and, in particular, efficient combinatorial optimization and counting. Our intention was to show how the SMC methods work in applications, while at the same time accentuating the unifying and novel mathematical ideas behind the SMC methods. We hope that the book stimulates further research at a postgraduate level.

The emphasis in this book is on concepts rather than on mathematical completeness. We assume that the reader has some basic mathematical background, such as a basic undergraduate course in probability and statistics. We have deliberately tried to avoid the formal “definition—lemma—theorem—proof” style of many mathematics books. Instead, we embed most definitions in the text and introduce and explain various concepts via examples and experiments.

Most of the combinatorial optimization and counting case studies in this book are benchmark problems taken from the World Wide Web. In all examples tested so far, the relative error of SMC was within the limits of 1–2% of the best-known solution. In some instances, SMC produced even more accurate solutions. The book covers the following topics:

Chapter 1 introduces the concepts of Monte Carlo methods for estimation and randomized algorithms to solve deterministic optimization and counting problems.

Chapter 2 deals with the cross-entropy method, which is able to approximate quite accurately the solutions to difficult estimation and optimization problems such as integer programming, continuous multiextremal optimization, noisy optimization problems such as optimal buffer allocation, optimal policy search, clustering, signal detection, DNA sequence alignment, network reliability optimization, and neural and reinforcement learning. Recently, the cross-entropy method has been used as a main engine for playing games such as Tetris, Go, and backgammon. For more references, see http://www.cemethod.org.

Chapter 3 presents the minimum cross-entropy method, also known as the MinxEnt method. Similar to the cross-entropy method, MinxEnt is able to deliver accurate solutions for difficult estimation and optimization problems. The main idea of MinxEnt is to associate with each original optimization problem an auxiliary single-constrained convex optimization program in terms of probability density functions. The beauty is that this auxiliary program has a closed-form solution, which becomes the optimal zero-variance solution, provided the “temperature” parameter is set to minus infinity. In addition, the associated probability density function based on the product of marginals obtained from the joint optimal zero variance probability density function coincides with the parametric probability density function of the cross-entropy method. Thus, we obtain a strong connection of the cross-entropy method with MinxEnt, providing solid mathematical foundations.

Chapter 4 introduces the splitting method for counting, combinatorial optimization, and rare-event estimation. Similar to the classic randomized algorithms, splitting algorithms use a sequential sampling plan to decompose a “difficult” problem into a sequence of “easy” ones. It presents, in fact, a combination of Markov chain Monte Carlo, like the Gibbs sampler, with a specially designed cloning mechanism. The latter runs in parallel multiple Markov chains by making sure that all of them run in steady-state at each iteration. This chapter contains the following elements:

• It combines splitting with the classic capture–recapture method in order to obtain low-variance estimators for counting in complex sets, such as counting the number of satisfiability assignments.
• It shows that the splitting algorithm can be efficiently used for estimating the reliability of complex static networks.
• It demonstrates numerically that the splitting algorithm can be efficiently used for generating uniform samples on discrete sets. We provide valid statistical tests supporting the uniformity of generated samples.
• It presents supportive numerical results, while solving quite general counting problems, such as counting the number of true assignments in a satisfiability problem, counting the number of feasible colorings in a graph, calculating the permanent, Hamiltonian cycles, 0-1 tables, and volume of a polytope, as well as solving integer and combinatorial optimization, like the traveling salesman, knapsack, and set-covering problems.

Chapter 5 presents a new generic sequential importance sampling algorithm, called stochastic enumeration for counting #P-complete problems, such as the number of satisfiability assignments, number of trajectories in a general network, and number of perfect matching in a graph. For this purpose, it employs a decision-making algorithm, also called an oracle. The crucial differences between stochastic enumeration and the other generic methods that we present in this book (i.e., cross-entropy, MinxEnt, and splitting) are:

• The former is sequential in nature (it is based on sequential importance sampling), whereas the latter are not (they sample simultaneously in the entire 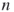-dimensional space).
• The former is based on decision-making oracles to solve #P-complete problems, whereas the latter are not. As a result, it is typically faster than the others.

We also present extensive numerical results with stochastic enumeration and show that it outperforms some of its well-known counterparts, in particular, the splitting method. Our explanation for that relies again on the fact that it uses sequential sampling and an oracle.

Appendix A provides auxiliary material. In particular, it covers some basic combinatorial and counting problems and supplies a background to the cross-entropy method. Finally, the efficiency of Monte Carlo estimators is discussed.

We thank all colleagues and friends who provided us with comments, corrections, and suggestions for improvements. We are grateful to the many undergraduate and graduate students at the Technion who helped make this book possible, and whose valuable ideas and experiments where extremely encouraging and motivating. We are especially indebted to Dirk Kroese, who worked through the entire manuscript and provided us a thorough review and feedback.

Ad Ridder

Radislav Vaisman

Amsterdam and Haifa

September 2013