Chapter 1

Introduction to Monte Carlo Methods

Monte Carlo methods present a class of computational algorithms that rely on repeated random sampling to approximate some unknown quantities. They are best suited for calculation using a computer program, and they are typically used when the exact results with a deterministic algorithm are not available.

The Monte Carlo method was developed in the 1940s by John von Neumann, Stanislaw Ulam, and Nicholas Metropolis while they were working on the Manhattan Project at the Los Alamos National Laboratory. It was named after the Monte Carlo Casino, a famous casino where Ulam's uncle often gambled away his money.

We mainly deal in this book with two well-known Monte Carlo methods, called importance sampling and splitting, and in particular with their applications to combinatorial optimization, counting, and estimation of probabilities of rare events.

Importance sampling is a well-known variance reduction technique in stochastic simulation studies. The idea behind importance sampling is that certain values of the input random variables have a greater impact on the output parameters than others. If these “important” values are sampled more frequently, the variance of the output estimator can be reduced. However, such direct use of importance sampling distributions will result in a biased estimator. To eliminate the bias, the simulation outputs must be modified (weighted) by using a likelihood ratio factor, also called the Radon Nikodym derivative [108]. The fundamental issue in implementing importance sampling is the choice of the importance sampling distribution.

In the case of counting problems, it is well known that a straightforward application of importance sampling typically yields poor approximations of the quantity of interest. In particular, Gogate and Dechter [56] [57] show that poorly chosen importance sampling in graphical models such as satisfiability models generates many useless zero-weight samples, which are often rejected, yielding an inefficient sampling process. To address this problem, which is called the problem of losing trajectories, these authors propose a clever sample search method, which is integrated into the importance sampling framework.

With regard to probability problems, a wide range of applications of importance sampling have been reported successfully in the literature over the last decades.Siegmund [115] was the first to argue that, using an exponential change of measure, asymptotically efficient importance sampling schemes can be built for estimating gambler's ruin probabilities. His analysis is related to the theory of large deviations, which has since become an important tool for the design of efficient Monte Carlo experiments. Importance sampling is now a subject of almost any standard book on Monte Carlo simulation (see, for example, [3] [108]). We shall use importance sampling widely in this book, especially in connection to rare-event estimation.

The splitting method dates back to Kahn and Harris [62] and Rosenbluth and Rosenbluth [97]. The main idea is to partition the state-space of a system into a series of nested subsets and to consider the rare event as the intersection of a nested sequence of events. When a given subset is entered by a sample trajectory during the simulation, numerous random retrials are generated, with the initial state for each retrial being the state of the system at the entry point. By doing so, the system trajectory is split into a number of new subtrajectories, hence the name “splitting”. Since then, hundreds of papers have been written on this topic, both from a theoretical and a practical point of view. Applications of the splitting method arise in particle transmission (Kahn and Harris [62]), queueing systems (Garvels [48], Garvels and Kroese [49], Garvels et al. [50]), and reliability (L'Ecuyer et al. [76]). The method has been given new impetus by the RESTART (Repetitive Simulation Trials After Reaching Thresholds) method in the sequence of papers by Villén-Altimirano and Villén-Altimirano [122–124]. A fundamental theory of the splitting method was developed by Melas [85], Glasserman et al. [54] [55], and Dean and Dupuis [38] [39]. Recent developments include the adaptive selection of the splitting levels in Cérou and Guyader [24], the use of splitting in reliability networks [73] [109], quasi-Monte Carlo estimators in L'Ecuyer et al. [77], and the connection between splitting for Markovian processes and interacting particle methods based on the Feynman-Kac model in Del Moral [89].

Let us introduce the notion of a randomized algorithm. A randomized algorithm is an algorithm that employs a degree of randomness as part of its logic to solve a deterministic problem such as a combinatorial optimization problem. As a result, the algorithm's output will be a random variable representing either the running time, its output, or both. In general, introducing randomness may result in an algorithm that is far simpler, more elegant, and sometimes even more efficient than the deterministic counterpart.

Suppose we are given three matrices , and and we want to check whether .

A trivial deterministic algorithm would be to run a standard multiplication algorithm and compare each entry of with . Simple matrix multiplication requires operations. A more sophisticated algorithm [88] takes only operations. Using randomization, however, we need only operations, with an extremely small probability of error [88].

• Pick a random -dimensional vector .
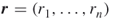• Multiply both sides of by 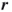, that is, obtain 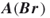and .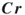
• If 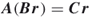, then declare 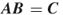, otherwise, .

This algorithm runs in operations because matrix multiplication is associative, so can be computed as , thus requiring only three matrix-vector multiplications for the algorithm.

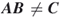For more examples and foundations on randomized algorithms, see the monographs [88] [90].

We shall consider not only randomized algorithms but also random structures. The latter comprises random graphs (such as Erdös-Rényi graphs), random Boolean formulas, and so on. Random structures are of interest both as a means of understanding the behavior of algorithms on typical inputs and as a mathematical framework in which one can investigate various probabilistic techniques to analyze randomized algorithms.

This book deals with Monte Carlo methods and their associated randomized algorithms for solving combinatorial optimization and counting problems. In particular, we consider combinatorial problems that can be modeled by integer linear constraints. To clarify, denote by the set of feasible solutions of a combinatorial problem, which is assumed to be a subset of an -dimensional integer vector space and which is given by the following linear constraints:

1.1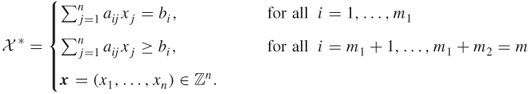

Here, is a given matrix and is a given -dimensional vector. Most often we require the variables to be nonnegative integers and, in particular, binary integers.

In this book, we describe in detail various problems, algorithms, and mathematical aspects that are associated with (1.1) and its relation to decision making, counting, and optimization. Below is a short list of problems associated with (1.1):

1. Decision making: Is nonempty?

2. Optimization: Solve for a given objective (performance) function .

3. Counting: Calculate the cardinality of .

It turns out that, typically, it is hard to solve any of the above three problems and, in particular, the counting one, which is the hardest one. However, we would like to point out that there are problems for which decision making is easy (polynomial time) but counting is hard [90]. As an example, finding a feasible path (and also the shortest path) between two fixed nodes in a network is easy, whereas counting the total number of paths between the two nodes is difficult. Some other examples of hard counting and easy decision-making problems include:

• How many different variable assignments will satisfy a given satisfiability formula in disjunctive normal form?
• How many different variable assignments will satisfy a given 2-satisfiability formula (constraints on pairs of variables)?
• How many perfect matchings are there for a given bipartite graph?

In Chapter 5, we follow the saying “counting is hard, but decision making is easy” and employ relevant decision-making algorithms, also called oracles, to derive fast Monte Carlo algorithms for counting.

Below is a detailed list of interesting hard counting problems.

• The Hamiltonian cycle problem. How many Hamiltonian cycles does a graph have? That is, how many tours contains a graph in which every node is visited exactly once (except for the beginning/end node)?
• The permanent problem. Calculate the permanent of a matrix 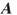, or equivalently, the number of perfect matchings in a bipartite balanced graph with 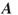as its biadjacency matrix.
• The self-avoiding walk problem. How many self-avoiding random walks of length 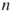exist, when we are allowed to move at each grid point in any neighboring direction with equal probability?
• The connectivity problem. Given two different nodes in a directed or undirected graph, say 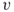and 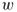, how many paths exist from 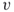to that do not traverse the same edge more than once?
• The satisfiability problem. Let be a collection of all sets of Boolean variables 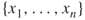. Thus, 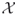has cardinality . Let 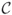be a set of 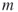Boolean disjunctive clauses. Examples of such clauses are 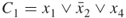, , 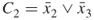etc. How many (if any) satisfying truth assignments for 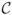exist, that is, how many ways are there to set the variables 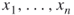either true or false so that all clauses 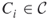are true?
• The 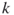-coloring problem. Given distinct colors, in how many different ways can one color the nodes (or the edges) of a graph, so that each two adjacent nodes (edges, respectively) in the graph have different colors?
• The spanning tree problem. How many unlabeled spanning trees has a graph 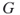? Note that this counting problem is easy for labeled graphs.
• The isomorphism problem. How many isomorphisms exist between two given graphs 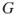and 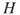? In other words, in an isomorphism problem one needs to find all mappings between the nodes of 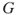and 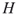such that is an edge of 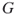if and only if 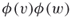is an edge of .
• The clique problem. How many cliques of fixed size 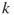exist in a graph 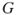? Recall that a clique is a complete subgraph of .

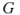The decision versions of these problems are all examples of NP-complete problems. Clearly, counting all feasible solutions, denoted by #P, is an even harder problem.

Generally, the complexity class #P consists of the counting problems associated with the decision problems in NP. Completeness is defined similarly to the decision problems: a problem is #P-complete if it is in #P, and if every #P problem can be reduced to it in polynomial counting reduction. Hence, the counting problems that we presented above are all #P-complete. For more details we refer the reader to the classic monograph by Papadimitrou and Stieglitz [92].