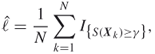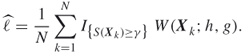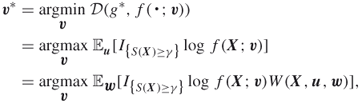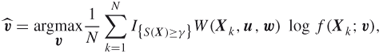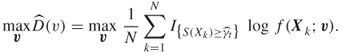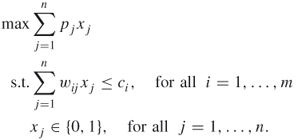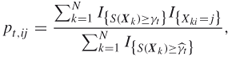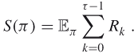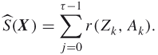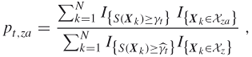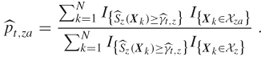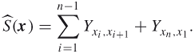Chapter 2
Cross-Entropy Method
2.1 Introduction
The cross-entropy (CE) method is a powerful technique for solving difficult estimation and optimization problems, based on Kullback-Leibler (or cross-entropy) minimization [15]. It was pioneered by Rubinstein in 1999 [100] as an adaptive importance sampling procedure for the estimation of rare-event probabilities. Subsequent work in [101] [102] has shown that many optimization problems can be translated into a rare-event estimation problem. As a result, the CE method can be utilized as randomized algorithms for optimization. The gist of the idea is that the probability of locating an optimal or near-optimal solution using naive random search is a rare event probability. The cross-entropy method can be used to gradually change the sampling distribution of the random search so that the rare event is more likely to occur. For this purpose, using the cross-entropy or Kullback-Leibler divergence as a measure of closeness between two sampling distributions, the method estimates a sequence of parametric sampling distributions that converges to a distribution with probability mass concentrated in a region of near-optimal solutions.
To date, the CE method has been successfully applied to optimization and estimation problems. The former includes mixed-integer nonlinear programming [69], continuous optimal control problems [111] [112], continuous multiextremal optimization [71], multidimensional independent component analysis [116], optimal policy search [19], clustering [11] [17, 72], signal detection [80], DNA sequence alignment [67] [93], fiber design [27], noisy optimization problems such as optimal buffer allocation [2], resource allocation in stochastic systems [31], network reliability optimization [70], vehicle routing optimization with stochastic demands [29], power system combinatorial optimization problems [45], and neural and reinforcement learning [81] [86, 118] [128]. CE has even been used as a main engine for playing games such as Tetris, Go, and backgammon [26].
In the estimation setting, the CE method can be viewed as an adaptive importance sampling procedure. In the optimization setting, the optimization problem is first translated into a rare-event estimation problem, and then the CE method for estimation is used as an adaptive algorithm to locate theoptimum.
The CE method is based on a simple iterative procedure where each iteration contains two phases: (a) generate a random data sample (trajectories, vectors, etc.) according to a specified mechanism; (b) update the parameters of the random mechanism on the basis of the data, in order to produce a “better” sample in the next iteration.
Among the two, optimization and estimation, CE is best known for optimization, for which it is able to handle problems of size up to thousands in a reasonable time limit. For estimation and also counting problems, multilevel CE can be useful only for problems of small and moderate size. The main reason for that is, unlike optimization, in estimation multilevel CE involves likelihood ratios factors for all variables. The well-known degeneracy of the likelihood ratio estimators [106] causes CE to perform poorly in high dimensions. To overcome this problem, [25] proposes a variation of the CE method by considering a single iteration for determining the importance sampling density. For this approach to work, one must be able to generate samples from the optimal (zero-variance) density.
A tutorial on the CE method is given in [37]. A comprehensive treatment can be found in [107]. The CE method website (www.cemethod.org) lists several hundred publications.
The rest of this chapter is organized as follows. Section 2.2 presents a general CE algorithm for the estimation of rare event probabilities, while Section 2.3 introduces a slight modification of this algorithm for solving combinatorial optimization problems. We consider applications of the CE method to the multidimensional knapsack problem, to the Mastermind game, and to Markov decision problems. Also, we provide supportive numerical results on the performance of the algorithm for these problems. Sections 2.4 and 2.5 discuss advanced versions of CE to deal with continuous and noisy optimization, respectively.
2.2 Estimation of Rare-Event Probabilities
Consider the problem of computing a probability of the form
for some fixed level 
. In this expression 
is the sample performance, and 
a random vector with probability density function (pdf) 
, sometimes called the prior pdf. The standard or crude Monte Carlo estimation method is based on repetitive sampling from 
and using the sample average:
where 
are independent and identically distributed (iid) samples drawn from 
. However, for rare-event probabilities, say 
or less, this method fails for the following reasons [108]. The efficiency of the estimator is measured by its relative error (RE), which is defined as
Clearly, for the standard estimator (2.2)
Thus, for small probabilities, meaning 
, we get
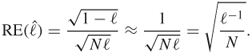
This says that the sample size 
is of the order 
to obtain relative error of 
. For rare-event probabilities, this sample size leads to unmanageable computation time. For instance, let 
be the maximum number of customers that during a busy period of an 
queue is present. For a load at 80%, the probability can be computed to be 
. A simulation to obtain relative error of 10% would require about 
samples of 
(busy cycles). On a 2.79 Ghz (0.99GB RAM) PC this would take about 18 days.
Assuming asymptotic normality of the estimator, the confidence intervals (CI) follow in a standard way. For example, a 95% CI for 
is given by
This shows again the reciprocal relationship between sample size and rare-event probability to obtain accuracy: suppose one wishes that the confidence half width is at most 
% relative to the estimate 
. This boils down to
For variance reduction we apply importance sampling simulation using pdf 
, that is, we draw independent and identically distributed samples 
from 
, calculate their likelihood ratios
and set the importance sampling estimator by
By writing 
, we see that this estimator is of the form 
. Again, we measure efficiency by its relative error, similar to (2.3), which might be estimated by 
, with
2.5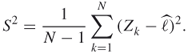 
being the sample variance of the 
.
In almost all realistic problems, the prior pdf 
belongs to a parameterized family
2.6 
That means that 
is given by some fixed parameter 
. Then it is natural to choose the importance sampling pdf 
from the same family using another parameter 
, or 
, etc. In that case the likelihood ratio becomes
2.7 
We refer to the original parameter 
as the nominal parameter of the problem, and we call parameters 
used in the importance sampling, the reference parameters.
that the shortest path from node 
to node 
in the network of Figure 2.1 has a length of at least 
. The random lengths 
of the links are assumed to be independent and exponentially distributed with means 
, respectively.
to 
.
, 
, and
the problem is cast in the framework of (2.1). Note that we can estimate (2.1) via (2.4) by drawing 
independently from exponential distributions that are possibly different from the original ones. That is, 
instead of 
, 
.
that gives the most accurate estimate of 
for a given simulation effort. To do so we use a two-stage procedure, where both the level 
and the reference parameters 
are updated simultaneously. As we shall soon see, one of the strengths of the CE method for rare-event simulation is that it provides a fast way to estimate accurately the optimal parameter vector 
.
The idea of the CE method is to choose the importance sampling pdf 
from within the parametric class of pdfs 
such that the Kullback-Leibler entropy between 
and the optimal (zero variance) importance sampling pdf 
, given by [107],
is minimal. The Kullback-Leibler divergence between 
and 
is given by
2.8 
The CE minimization procedure then reduces to finding an optimal reference parameter, 
, say by cross-entropy minimization:
where 
is any reference parameter and the subscript in the expectation operator indicates the density of 
. This 
can be estimated via the stochastic counterpart of (2.9):
where 
are drawn from 
.
The optimal parameter 
in (2.10) can often be obtained in explicit form, in particular when the class of sampling distributions forms an exponential family [[107], pages 319–320]. Indeed, analytical updating formulas can be found whenever explicit expressions for the maximal likelihood estimators of the parameters can be found [[37], page 36].
In the other cases, we consider a multilevel approach, where we generate a sequence of reference parameters 
and a sequence of levels 
, while iterating in both 
and 
. Our ultimate goal is to have 
close to 
after some number of iterations and to use 
in the importance sampling density 
to estimate 
.
We start with 
and choose 
to be a not too small number, say 
. At the first iteration, we choose 
to be the optimal parameter for estimating 
, where 
is the 
-quantile of 
. That is, 
is the largest real number for which 
Thus, if we simulate under 
, then level 
is reached with a reasonably high probability of around 
. In this way we can estimate the (unknown!) level 
, simply by generating a random sample 
from 
, and calculating the 
-quantile of the order statistics of the performances 
; that is, denote the ordered set of performance values by 
, then
where 
denotes the integer part. Next, the reference parameter 
can be estimated via (2.10), replacing 
with the estimate of 
. Note that we can use here the same sample for estimating both 
and 
. This means that 
is estimated on the basis of the 
best samples, that is, the samples 
for which 
is greater than or equal to 
. These form the elite samples in the first iteration. We repeat these steps in the subsequent iterations. The two updating phases, starting from 
are given below:
. For a fixed 
, let 
be the 
-quantile of 
under 
. To estimate 
, draw a random sample 
from 
and evaluate the sample 
-quantile 
.
. For fixed 
and 
, derive 
as
and 
, derive 
as the solution
is the set of elite samples in the 
-th iteration, that is, the samples 
for which 
.The procedure terminates when at some iteration 
a level 
is reached that is at least 
, and thus the original value of 
can be used without getting too few samples. We then reset 
to 
, reset the corresponding elite set, and deliver the final reference parameter 
, using again (2.12). This 
is then used in (2.4) to estimate 
.
. The advantage is that it does not involve the likelihood ratio in this optimization program.Instead of updating the parameter vector 
directly via (2.12), we use the following smoothed version:
where 
is the parameter vector given in (2.12), and 
is called the smoothing parameter, typically with 
. Clearly, for 
we have our original updating rule. The reason for using the smoothed (2.13) instead of the original updating rule is twofold: (a) to smooth out the values of 
, (b) to reduce the probability that some component 
of 
will be zero or one at the first few iterations. This is particularly important when 
is a vector or matrix of probabilities. Because in those cases, when 
it is always ensured that 
, while for 
one might have (even at the first iterations) that either 
or 
for some indices 
. As a result, the algorithm will converge to a wrong solution.
The resulting CE algorithm for rare-event probability estimation can thus be written as follows.
. Let 
. Set 
(iteration counter).
according to the pdf 
for all 
, and order them from smallest to biggest, 
. Let 
be the sample 
-quantile of performances: 
. If 
reset 
to 
.
to solve the stochastic program (2.12).
.
, set 
and reiterate from step 2. Else proceed with step 7.
be the final iteration counter. Generate a sample 
according to the pdf 
and estimate 
via (2.4).Apart from specifying the family of sampling pdfs, the sample sizes 
and 
, and the rarity parameter 
, the algorithm is completely self-tuning. The sample size 
for determining a good reference parameter can usually be chosen much smaller than the sample size 
for the final importance sampling estimation, say 
versus 
= 100,000. Under certain technical conditions [107], the deterministic version of Algorithm 2.1 is guaranteed to terminate (reach level 
) provided that 
is chosen small enough.
Note that Algorithm 2.1 breaks down the “hard” problem of estimating the very small probability 
into a sequence of “simple” problems, generating a sequence of pairs 
, depending on 
, which is called the rarity parameter. Convergence of Algorithm 2.1 is discussed in [107]. Other convergence proofs for the CE method may be found in [33] and [84].
Optimization problems of the form (2.12) appear frequently in statistics. In particular, if the 
factor is omitted, which will turn out to be important in CE optimization, one can write (2.12) also as
where the product is the joint density of the elite samples. Consequently, 
is chosen such that the joint density of the elite samples is maximized. Viewed as a function of the parameter 
, rather than the data 
, this function is called the likelihood. In other words, 
is the maximum likelihood estimator (it maximizes the likelihood) of 
based on the elite samples. When the 
factor is present, the form of the updating formula remains similar.
To provide further insight into Algorithm 2.1, we shall follow it step-by-step in a couple of toy examples.
, where 
, 
is the success probability, and 
is the target threshold. Suppose that 
is large compared to the mean 
, so that
is a rare-event probability. Assume further that 
is fixed and we want to estimate the optimal parameter 
in 
using (2.12).
, we sample independent and identically distributed 
. The right-hand side of (2.12) becomes
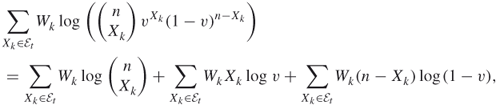
where
is the likelihood ratio of the 
-th sample. To find the optimal 
, we consider the first-order condition. We obtain
yields
In other words, 
is simply the sample fraction of the elite samples, weighted by the likelihood ratios. Note that, without the weights 
, we would obtain the maximum likelihood estimator of 
for the 
distribution based on the elite samples, in accordance with Remark 2.5. Note also that (2.14) can be viewed as a stochastic counterpart of the deterministic updating formula
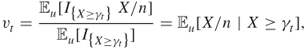
where 
is the 
-quantile of the 
distribution.
, 
, and 
, which corresponds to 
. Table 2.1 presents the evolution of 
and 
for 
, using sample size 
. Note that iteration 
corresponds to the original binomial pdf withsuccess probability 
, while iterations 
correspond to binomial pdfs with success probabilities 
respectively.
and 
for 
, using 
and 
samples |
 |
 |
| 0 | — | 0.1667 |
| 1 | 23 | 0.2530 |
| 2 | 33 | 0.3376 |
| 3 | 42 | 0.4263 |
| 4 | 51 | 0.5124 |
| 5 | 50 | 0.5028 |
, using a sample size 
that is typically larger than 
. Clearly, we reset the 
obtained in the last iteration to 
.
. Note that until iteration 4 both parameters 
and 
increase gradually, each time “blowing up” the tail of the binomial pdf. At iteration five we reset the value 
to the desired 
and estimate the optimal 
value.
samples from 
, estimates level 
, and estimates the next sampling parameter 
.
is the maximum of 
, no “overshooting” of 
in Algorithm 2.1 will occur, and therefore 
does not need to be reset. In such cases, the sampling pdf may degenerate towards the atomic pdf that has all its mass concentrated at the points 
where 
is maximal. As an example, let 
be the target level in the above binomial example. In this case, clearly the final 
, which corresponds to the degenerate value of 
. Table 2.2 and Figure 2.3 show the evolution of the parameters in the CE algorithm, using 
and 
.
and 
for the 
Example using 
, 
and 
samples
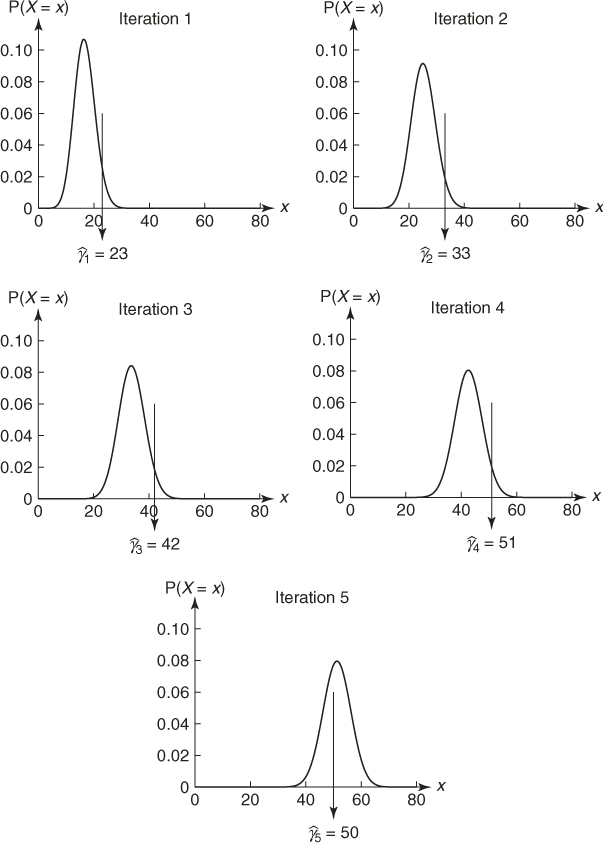
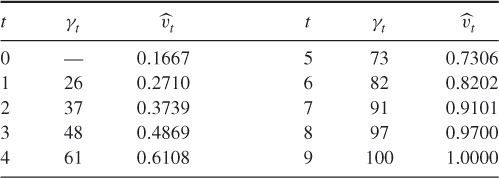
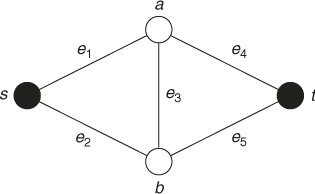
as the nominal parameter and estimate the probability 
that the minimum path length is greater than 
.
samples—very large simulation effort—gave an estimate 
with an estimated relative error of 
.
. Since the components 
are independent and form an exponential family parameterized by the mean we have [107]2.15 
given in (2.10).
, the sample size for step 2–4 of the algorithm 
, and for the final sample size 
. Table 2.3 displays the results of steps 1–5 of the CE algorithm.
in Example 2.4.
is reached. As before, we set 
to the desired 
and estimate the optimal parameter vector 
, which is 
= 
. Using 
we obtain 
= 
, with an estimated RE of 
. The same RE was obtained for the crude Monte Carlo with 
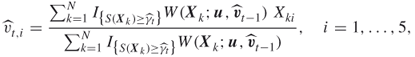
samples. Note that, whereas the standard method required more than an hour of computation time, the CE algorithm was finished in only 1 second, using a Matlab implementation on a 1500 MHz computer. We see that with a minimal amount of work we have achieved a dramatic reduction of the simulation effort.2.3 Cross-Entropy Method forOptimization
Consider the following optimization problem:
having 
as the set of optimal solutions.
The problem is called a discrete or continuous optimization problem, depending on whether 
is discrete or continuous. An optimization problem where some 
are discrete and some others are continuous variables is called a mixed optimization problem. An optimization problem with a finite state space (
) is called a combinatorial optimization problem. The latter will be the main focus of this section.
We will show here how the cross-entropy method can be applied for approximating a pdf 
that is concentrated on 
. In fact, the iterations of the cross-entropy algorithm generate a sequence of pdfs 
associated with a sequence of decreasing sets converging to 
.
Suppose that we set the optimal value 
, then an optimal pdf 
is characterized by
This matches exactly to the case of degeneracy of the cross-entropy algorithm for rare-event simulation in Example 2.7.
Hence, the starting point is to associate with the optimization problem (2.16) a meaningful estimation problem. To this end, we define a collection of indicator functions 
on 
for various levels 
. Next, let 
be a family of probability densities on 
, parameterized by real-valued parameters 
. For a fixed 
we associate with (2.16) the problem of estimating the rare-event probability
We call the estimation problem (2.17) the associated stochastic problem.
It is important to understand that one of the main goals of CE in optimization is to generate a sequence of pdfs 
, converging to a pdf 
that is close or equal to an optimal pdf 
. For this purpose we apply Algorithm 2.1 for rare-event estimation, but without fixing in advance 
. It is plausible that if 
is close to 
, then 
assigns most of its probability mass on 
, and thus any 
drawn from this distribution can be used as an approximation to an optimal solution 
, and the corresponding function value as an approximation to the true optimal 
in (2.16).
In summary, to solve a combinatorial optimization problem we will employ the CE Algorithm 2.1 for rare-event estimation without fixing 
in advance. By doing so, the CE algorithm for optimization can be viewed as a modified version of Algorithm 2.1. In particular, in analogy to Algorithm 2.1, we choose a not very small number 
, say 
, initialize the parameter 
by setting 
, and proceed as follows:
. For a fixed 
, let 
be the 
-quantile of 
under 
. As before, an estimator 
of 
can be obtained by drawing a random sample 
from 
and then evaluating the sample 
-quantile of the performances as
. For fixed 
and 
, derive 
from the solution of the program
and 
, derive 
from the following program:
Note that, in contrast to the formulas (2.11) and (2.12) (for the rare-event setting), formulas (2.19) and (2.20) do not contain the likelihood ratio factors 
. The reason is that in the rare-event setting, the initial (nominal) parameter 
is specified in advance and is an essential part of the estimation problem. In contrast, the initial reference vector 
in the associated stochastic problem is quite arbitrary. In effect, by dropping the likelihood ratio factor, we can efficiently estimate at each iteration 
the CE optimal high-dimensional reference parameter vector 
for the rare event probability 
by avoiding the degeneracy properties of the likelihood ratio.
Thus, the main CE optimization algorithm, which includes smoothed updating of parameter vector 
and which presents a slight modification of Algorithm 2.1 can be summarized as follows.
. Set 
(level counter).
from the density 
.
-quantile 
of the performances according to (
and solve the stochastic program (2.20). Denote the solution by 
.
.
, and return to Step 2.Note that when 
must be minimized instead of maximized, we simply change the inequalities “
” to “
” and take the 
-quantile instead of the 
-quantile. Alternatively, one can just maximize 
.
, say 
,
then stop.
As an alternative estimate for 
, one can consider
2.22 
Before one implements the algorithm, one must decide on specifying the initial vector 
, the sample size 
, the stopping parameter 
, and the rarity parameter 
. However, the execution of the algorithm is “self-tuning.”
Note that the estimation Step 7 of Algorithm 2.1 is omitted in Algorithm 2.2, because, in the optimization setting, we are not interested in estimating 
per se.
, the initial vector 
, the sample size 
, the rarity parameter 
, and a stopping criterion. Of these, the most challenging is the selection of an appropriate class of parametric sampling densities 
. Typically, there is not a unique parametric family and the selection is guided by the following competing objectives. First, the class 
has to be flexible enough to include a reasonable parametric approximation to an optimal importance sampling density 
for the estimation of the associated rare-event probability 
. Second, each density 
has to be simple enough to allow fast random variable generation. In many cases, these two competing objectives are reconciled by using a standard statistical model for 
, such as the multivariate Bernoulli or Gaussian densities with independent components of the vector 
.Algorithm 2.2 can, in principle, be applied to any discrete optimization problem. However, for each individual problem, two essential ingredients need to be supplied:
.
, based on cross-entropy minimization program (2.20), which is the same for all optimization problems.In general, there are many ways to generate samples from 
, and it is not always immediately clear which way of generating the sample will yield better results or easier updating formulas.
and the rarity parameter 
depends on the size of the problem and the number of parameters in the associated stochastic problem. Typical choices are 
or 
and 
, where 
is the number of parameters that need to be estimated/updated and 
is a constant between 1 and 10.Below we present several applications of the CE method to combinatorial optimization problems, namely to the multidimensional 0/1 knapsack problem, the mastermind game, and to reinforcement learning in Markov decision problems. We demonstrate numerically the efficiency of the CE method and its fast convergence for several case studies. For additional applications of CE, see [107].
2.3.1 The Multidimensional 0/1 Knapsack Problem
Consider the multidimensional 0/1 knapsack problem (see Section A.1.2):
In other words, the goal is to maximize the performance function 
over the set 
given by the knapsack constraints of (2.23).
Note that each item 
is either chosen, 
, or left out, 
. We model this by a Bernoulli random variable 
, with parameter 
. By setting these variables independent, we get the following parameterized set:
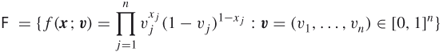
of Bernoulli pdfs. The optimal solution 
of the knapsack problem (2.23) is characterized by a degenerate pdf 
for which all 
; that is,
To proceed, consider the stochastic program 2.20. We have
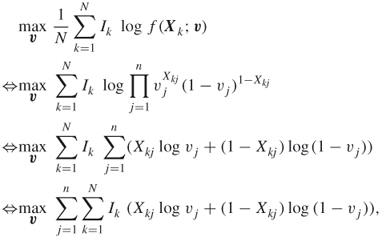
where, for convenience, we write 
. Applying the first-order optimality conditions we have
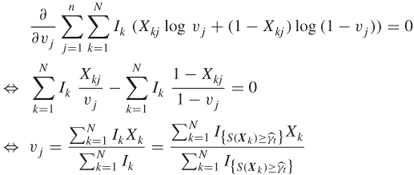
for 
.
As a concrete example, consider the knapsack problem; available at http://people.brunel.ac.uk/∼mastjjb/jeb/orlib/mknapinfo.html from the OR Library involving 
variables and 
constraints. In this problem the vector 
is
and the matrix 
and the vector 
are
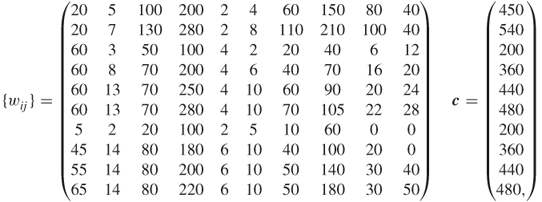
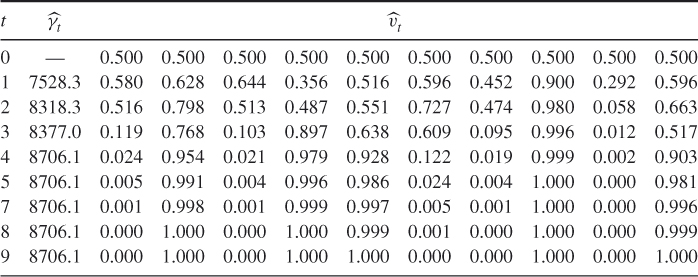
The performance of the CE algorithm is illustrated in Table 2.4 using the sample size 
, rarity parameter 
, and smoothing parameter 
. The initial probabilities were all set to 
. Observe that the probability vector 
quickly converges to a degenerate one, corresponding to the solution 
with value 
, which is also the optimal known value 
. Hence, the optimal solution has been found.
Table 2.4 The evolution of 
and 
for the 
-Knapsack Example, using 
, 
, and 
samples
2.3.2 Mastermind Game
In the well-known game Mastermind, the objective is to decipher a hidden “code” of colored pegs through a series of guesses. After each guess, new information on the true code is provided in the form of black and white pegs. A black peg is earned for each peg that is exactly right and a white peg for each peg that is in the solution, but in the wrong position; see Figure 2.4. To get a feel for the game, one can visit www.archimedes-lab.org/mastermind.html and play the game.
Figure 2.4 The Mastermind game.
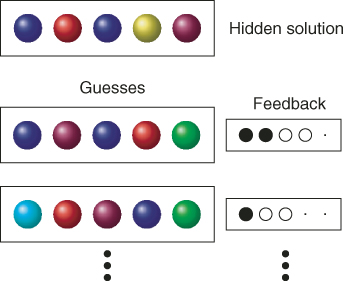
Consider a Mastermind game with 
colors, numbered 
and 
pegs (positions). The hidden solution and a guess can be represented by a row vector of length 
with numbers in 
. For example, for 
and 
the solution could be 
, and a possible guess 
. Let 
be the space of all possible guesses; clearly 
. On 
we define a performance function 
that returns for each guess 
the “pegscore”
where 
and 
are the number of black and white pegs returned after the guess, 
. We have assumed, somewhat arbitrarily, that a black peg is worth twice as much as a white peg. As an example, for the solution 
and guess 
above one gets two black pegs (for the first and third pegs in the guess) and two white pegs (for the second and fourth pegs in the guess, which match the fifth and second pegs of the solution but are in the wrong place). Hence the score for this guess is 6.
There are some specially designed algorithms that efficiently solve the problem for different number of colors and pegs. For examples, see www.mathworks.com/contest/mastermind.cgi/home.html.
Note that, with the above performance function, the problem can be formulated as an optimization problem, that is, as 
, and hence we could apply the CE method to solve it. In order to apply the CE method we first need to generate random guesses 
using an 
probability matrix 
. Each element 
of 
describes the probability that we choose the 
th color for the 
th peg (location). Since only one color may be assigned to one peg, we have that
2.25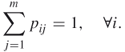 
In each stage 
of the CE algorithm, we sample independently for each row (that is, each peg) a color using a probability matrix 
and calculate the score 
according to (2.24). The updating of the elements 
of the probability matrix 
is performed according to
where the samples 
are drawn independently and identically distributed using matrix 
. Note that in this case 
in (2.26) simply counts the fraction of times among the elites that color 
has been assigned to peg 
.
2.3.2.1 Simulation Results
Table 2.5 represents the dynamics of the CE algorithm for the Mastermind test problem denoted at www.mathworks.com/contest/mastermind.cgi/home.html as “problem (5.2.3)” with the matrix 
of size 
. We used 
, 
, and 
. It took 34 seconds of CPU time to find the true solution.
Table 2.5 Dynamics of Algorithm 2.2 for the mastermind problem with 
colors and 
pegs. In each iteration 
was the sampled maximal score
 |
 |
 |
| 1 | 31 | 26 |
| 2 | 34 | 28 |
| 3 | 38 | 32 |
| 4 | 42 | 35 |
| 5 | 48 | 40 |
| 6 | 55 | 45 |
| 7 | 60 | 51 |
| 8 | 64 | 57 |
| 9 | 70 | 63 |
| 10 | 72 | 68 |
| 11 | 72 | 72 |
2.3.3 Markov Decision Process and Reinforcement Learning
The Markov decision process (MDP) model is standard in machine learning, operations research, and related fields. The application to reinforcement learning in this section is based on [83]. We start by reviewing briefly some of the basic definitions and concepts in MDP. For details see, for example, [95].
An MDP is defined by a tuple 
where
is a finite set of states.
is the set of possible actions by the decision maker. We assume it is the same for every state, to ease notations.
is the transition probability matrix with elements 
presenting the transition probability from state 
to state 
, when action 
is chosen.
is the immediate reward for performing action 
in state 
(
may be a random variable).At each time instance 
, the decision maker observes the current state 
and determines the action to be taken (say 
). As a result, a reward given by 
is received immediately, and a new state 
is chosen according to 
. A policy or strategy 
is a rule that determines, for each history 
of states and actions, the probability distribution of the decision maker's actions at time 
. A policy is called Markov if each action depends only on the current state 
. A Markov policy is called stationary if it does not depend on the time 
. If the decision rule 
of a stationary policy is nonrandomized, we say that the policy is deterministic.
In the sequel, we consider problems for which an optimal policy belongs to the class of stationary Markov policies. Associated with such a MDP are the stochastic processes of consecutive observed states 
and actions 
. For stationary policies we may denote 
, which is a random variable on the action set 
. In case of deterministic policies it degenerates in a single action. Finally, we denote the immediate rewards in state 
by 
.
The goal of the decision maker is to maximize a certain reward function. The following are standard reward criteria:
(random or deterministic) at which the process terminates. The objective is to maximize the total reward
denotes the expectation with respect to the probability measure induced by the strategy 
.
that maximizes2.28 
is the discount factor.
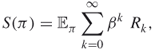
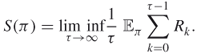
Suppose that the MDP is identified; that is, the transition probabilities and the immediate rewards are specified and known. Then it is well known that there exists a deterministic stationary optimal strategy for the above three cases. Moreover, there are several efficient methods for finding it, such as value iteration and policy iteration [95].
In the next section, we will restrict our attention to the stochastic shortest path MDP, where it is assumed that the process starts from a specific initial state 
and terminates in an absorbing state 
with zero reward. For the finite horizon reward criterion 
is the time at which 
is reached (which we will assume will always happen eventually). It is well known that for the shortest path MDPthere exists a stationary Markov policy that maximizes 
for each of the reward functions above.
However, when the transition probability or the reward in an MDP are unknown, the problem is much more difficult and is referred to as a learning probability. A well-known framework for learning algorithms is reinforcement learning (RL), where an agent learns the behavior of the system through trial-and-error with an unknown dynamic environment; see [61].
There are several approaches to RL, which can be roughly divided into the following three classes: model-based, model-free, and policy search. In the model-based approach, a model of the environment is first constructed. The estimated MDP is then solved using standard tools of dynamic programming (see [66]).
In the model-free approach, one learns a utility function instead of learning the model. The optimal policy is to choose at each state an action that maximizes the expected utility. The popular Q-learning algorithm (e.g., [125]) is an example of this approach.
In the policy search approach, a subspace of the policy space is searched, and the performance of policies is evaluated based on their empirical performance (e.g., [7]). An example of a gradient-based policy search method is the REINFORCE algorithm of [127]. For a direct search in the policy space approach see [98]. The CE algorithm in the next section belongs to the policy search approach.
of a nonlinear equation 
, where 
is a random variable with a pdf parameterized by 
, such that its expectation 
is not available in closed form. However, assume that we can simulate 
for any parameter 
. The SA algorithm for estimating 
is
where 
is a positive sequence satisfying
2.29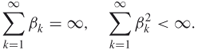 
remains bounded away from 0 (and thus convergence is not guaranteed), it is still required that 
is small in order to ensure convergence to a reasonable neighboring solution [10].2.3.3.1 Policy Learning via the CE Method
We consider a CE learning algorithm for the shortest path MDP, where it is assumed that the process starts from a specific initial state 
, and that there is an absorbing state 
with zero reward. The objective is given in (2.27), with 
being the stopping time at which 
is reached (which we will assume will always happen).
To put this problem in the CE framework, consider the maximization problem (2.27). Recall that for the shortest path MDP an optimal stationary strategy exists. We can represent each stationary strategy as a vector 
with 
being the action taken when visiting state 
. Writing the expectation in (2.27) as
2.30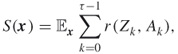 
we see that the optimization problem (2.27) is of the form 
. We shall also consider the case where 
is measured (observed) with some noise, in which case we have a noisy optimization problem.
The idea now is to combine the random policy generation and the random trajectory generation in the following way: At each stage of the CE algorithm we generate random policies and random trajectories using an auxiliary 
matrix 
, such that for each state 
we choose action 
with probability 
. Once this “policy matrix” 
is defined, each iteration of the CE algorithm comprises the following two standard phases:
random trajectories 
using the auxiliary policy matrix 
. The cost of each trajectory is computed via
) on the basis of the data collected in the first phase.The matrix 
is typically initialized to a uniform matrix (
.) We describe both the trajectory generation and updating procedure in more detail. We shall show that in calculating the associated sample performance, one can take into account the Markovian nature of the problem and speed up the Monte Carlo process.
2.3.3.2 Generating Random Trajectories
Generation of random trajectories for MDP is straightforward and is given for convenience only. All one has to do is to start the trajectory from the initial state 
and follow the trajectory by generating at each new state according to the probability distribution of 
, until the absorbing state 
is reached at, say, time 
,
auxiliary policy matrix.
, set 
.
according to the 
th row of 
, calculate the reward 
, and generate a new state 
according to 
. Set 
. Repeat until 
.
given by (2.31).2.3.3.3 Updating Rules
Let the 
trajectories 
, their scores, 
, and the associated 
-quantile 
of their order statistics be given. Then one can update the parameter matrix 
using the CE method, namely as per
where the event 
means that the trajectory 
contains a visit to state 
and the event 
means the trajectory corresponding to policy 
contains a visit to state 
in which action 
was taken.
We now explain how to take advantage of the Markovian nature of the problem. Let us think of a maze where a certain trajectory starts badly, that is, the path is not efficient in the beginning, but after some time it starts moving quickly toward, the goal. According to (2.32), all the updates are performed in a similar manner in every state in the trajectory. However, the actions taken in the states that were sampled near the target were successful, so one would like to “encourage” these actions. Using the Markovian property one can substantially improve the above algorithm by considering for each state the part of the reward from the visit to that state onward. We therefore use the same trajectory and simultaneously calculate the performance for every state in the trajectory separately. The idea is that each choice of action in a given state affects the reward from that point on, regardless of the past.
The sampling Algorithm 2.3 does not change in steps 1 and 2. The difference is in step 3. Given a policy 
and trajectory 
, we calculate the performance from every state until termination. For every state 
in the trajectory, the (estimated) performance is 
. The updating formula for 
is similar to (2.32), however, each state 
is updated separately according to the (estimated) performance 
obtained from state 
onward.
It is important to understand here that, in contrast to (2.32), the CE optimization is carried for every state separately and a different threshold parameter 
is used for every state 
, at iteration 
. This facilitates faster convergence for “easy” states where the optimal strategy is easy to find. The above trajectory sampling method can be viewed as a variance reduction method. Numerical results indicate that the CE algorithm with updating (2.33) is much faster than that with updating (2.32).
2.3.3.4 Numerical Results with the Maze Problem
The CE Algorithm with the updating rule (2.33) and trajectory generation according to Algorithm 2.3 was tested for a stochastic shortest path MDP and, in particular, for a maze problem, which presents a two-dimensional grid world. The agent moves on a grid in four possible directions. The goal of the agent is to move from the upper-left corner (the starting state) to the lower-right corner (the goal) in the shortest path possible. The maze contains obstacles (walls) into which movement is not allowed. These are modeled as forbidden moves for the agent.
We assume the following:
and 
. The cost of forbidden moves are random variables uniformly distributed between 25 and 75. Thus, the expected costs are 1 and 50 for the allowed and forbidden moves, respectively.In addition, we introduce the following:
- A small (failure) probability not to succeed moving in an allowed direction
- A small probability of succeeding moving in the forbidden direction (“moving through the wall”)
In Figure 2.5 we present the results for 
maze. We set the following parameters: 
, 
, 
.
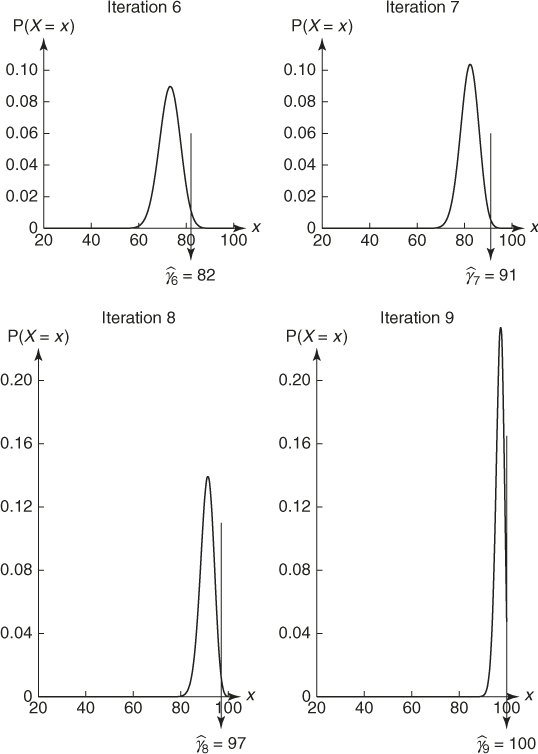
Figure 2.5 Performance of the CE Algorithm for the 
maze. Each arrow indicates a probability 
of going in that direction.
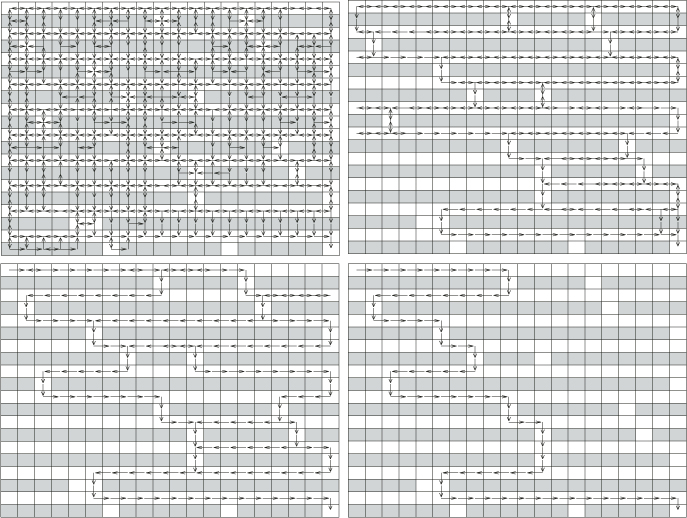
The initial policy was a uniformly random one. The success probabilities in the allowed and forbidden states were taken to be 0.95 and 0.05, respectively. The arrows 
in Figure 2.5 indicate that at the current iteration the probability of going from 
to 
is at least 0.01. In other words, if 
corresponds to the action that will lead to state 
from 
then we will plot an arrow from 
to 
provided 
.
In all our experiments, CE found the target exactly, within 5–10 iterations, and CPU time was less than one minute (on a 500MHz Pentium processor). Note that the successive iterations of the policy in Figure 2.5 quickly converge to the optimal policy. We have also run the algorithm for several other mazes and the optimal policy was always found.
2.4 Continuous Optimization
When the state space is continuous, in particular, when 
, the optimization problem (2.16) is often referred to as a continuous optimization problem. The CE sampling distribution on 
can be quite arbitrary and does not need to be related to the function that is being optimized. The generation of a random vector 
in Step 2 of Algorithm 2.2 is most easily performed by drawing the 
coordinates independently from some two-parameter distribution. In most applications a normal (Gaussian) distribution is employed for each component. Thus, the sampling density 
of 
is characterized by a vector of means 
and a vector of variances 
(and we may write 
). The choice of the normal distribution is motivated by the availability of fast normal random number generators on modern statistical software and the fact that the cross-entropy minimization yields a very simple solution—at each iteration of the CE algorithm the parameter vectors 
and 
are the vectors of sample means and sample variance of the elements of the set of 
best-performing vectors (that is, the elite set); see, for example, [71]. In summary, the CE method for continuous optimization with a Gaussian sampling density is as follows.
and 
. Set 
.
from the 
distribution.
be the indices of the 
best performing (elite) samples.
let2.34 
2.36 
, and return 
(or the overall best solution generated by the algorithm) as the approximate solution to the optimization. Otherwise, increase 
by 
and return to Step 2.Smoothing, as in Step 5, is often crucial to prevent premature shrinking of the sampling distribution. Instead of using a single smoothing factor, it is often useful to use separate smoothing factors for 
and 
(see (2.35)). In particular, it is suggested in [108] to use the following dynamic smoothing for 
:
2.37 
where 
is an integer (typically between 5 and 10) and 
is a smoothing constant (typically between 0.8 and 0.99). Finally, significant speed-up, can be achieved by using a parallel implementation of CE [46].
Another approach is to inject extra variance into the sampling distribution, for example, by increasing the components of 
, once the distribution has degenerated; see the examples below and [11].
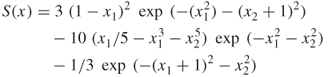
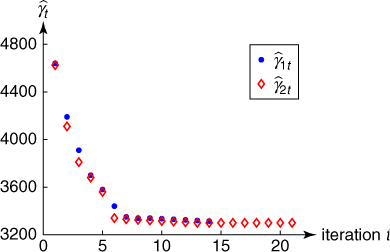
has various local maxima. In this case, implementing the CE Algorithm 2.4 we found that the global maximum of this function is approximately 
and is attained at 
. The choice of the initial value for 
is not important, but the initial standard deviations should be chosen large enough to ensure initially a “uniform” sampling of the region of interest. The CE algorithm is stopped when all standard deviations of the sampling distribution are less than some small 
.
and 
, for each iteration 
. We see that the values quickly converge to the optimal value 
.
denote the best performance found at the 
-th iteration, and (in the normal case) 
the largest standard deviation at the 
-th iteration. If 
is sufficiently small and 
is also small, then add some small value to each standard deviation, for example, a constant 
or the value 
, for some fixed 
and 
. When using CE with injection, a possible stopping criterion is to stop when a certain number of injections is reached.2.5 Noisy Optimization
One of the distinguishing features of the CE Algorithm 2.2 is that it can easily handle noisy optimization problems, that is, when the objective function 
is corrupted with noise. We denote such noisy function as 
and assume that for each 
we can readily obtain an outcome of 
, for example, via generation of some additional random vector 
, whose distribution may depend on 
.
A classical example of noisy optimization is simulation-based optimization [107]. A typical instance is the buffer allocation problem (BAP). The objective in the BAP is to allocate 
buffer spaces among the 
“niches” (storage areas) between 
machines in a serial production line, so as to optimize some performance measure, such as the steady-state throughput. This performance measure is typically not available analytically and thus must be estimated via simulation. A detailed description of the BAP with application of CE is given in [107].
Another example is the noisy traveling salesman problem (TSP), where, say, the cost matrix 
, denoted now by 
, is random. Think of 
as the “random” time to travel from city 
to city 
.
The total cost of a tour 
is given by
We assume that 
.
The main CE optimization Algorithm 2.2 for deterministic functions 
is valid also for noisy ones 
. Extensive numerical studies [107] with such noisy Algorithm 2.2 show that it works nicely because, during the course of optimization, it filters out efficiently the noise component from 
.
We applied our CE Algorithm 2.2 to both deterministic and noisy TSP. We selected a number of benchmark problems from the TSP library (www.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95/tsp/). In all cases, the same set of CE parameters were chosen: 
, 
, 
. Table 2.6 presents the performance of the deterministic version of Algorithm 2.2 for several TSPs from this library. To study the variability in the solutions, each problem was repeated 10 times. In Table 2.6, “min”, “mean”, and “max” denote the smallest (that is, best), average, and largest of the 10 estimates for the optimal value. The best-known solution is denoted by 
.
Table 2.6 Case studies for the TSP
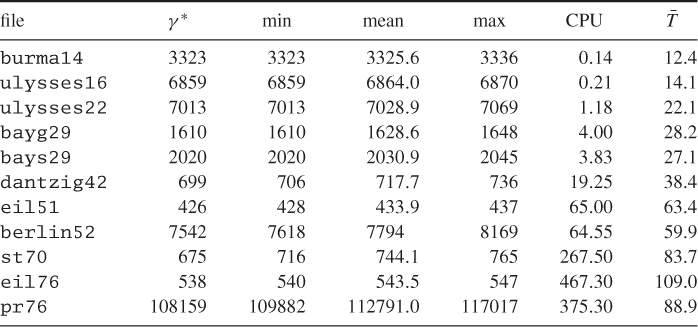
The average CPU time in seconds and the average number of iterations are given in the last two columns. The size of the problem (number of nodes) is indicated in its name. For example, st70 has 
nodes.
to 
is given by 
, where 
is the cost for the deterministic case. The expected cost is thus 
, and the total cost 
of a tour 
is given by (2.38). The CE algorithm for optimizing the unknown 
remains exactly the same as in the deterministic case, except that 
is replaced with 
, and that a different stopping criterion than (2.21) needs to be employed. A simple rule is to stop when the transition probabilities 
satisfy 
for all 
and 
. An alternative stopping rule taken from [107] is as follows.
, denote by 
and 
the worst of the elite samples (
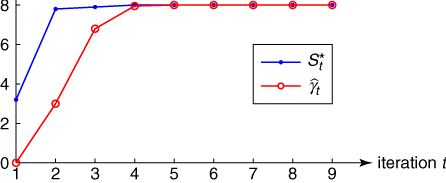
) for both the deterministic and noisy case, respectively, and we consider the following moving average-process:2.39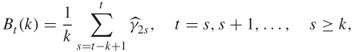 
where 
is fixed, say 
. Define next
2.40 
and
2.41 
respectively, where 
is fixed, say 
. Clearly, for 
and moderate 
and 
, we may expect that 
, provided the variance of 
is bounded.
2.42 
where 
and 
are fixed and 
is a small number, say 
.
) for both the deterministic and noisy case, denoted by 
and 
, respectively. We see in both cases a similar rapid drop in the level 
. It is important to note, however, that even though the algorithm in both the deterministic and noisy case converges to the optimal solution, the 
for the noisy case do not converge to 
, in contrast to the 
for the deterministic case. This is because the latter eventually estimates the 
-quantile of the deterministic 
, whereas the former estimates the 
-quantile of 
, which is random. To estimate 
in the noisy case, one needs to take the sample average of 
, where 
is the solution found at the final iteration.