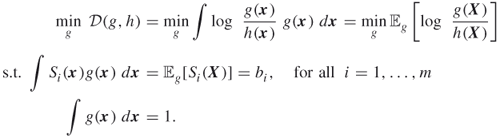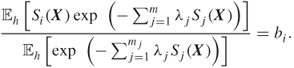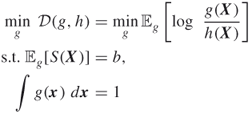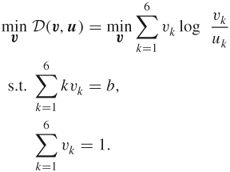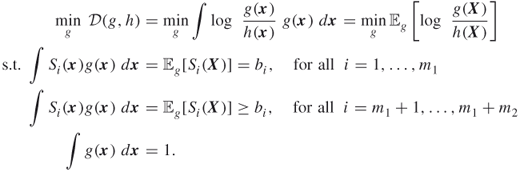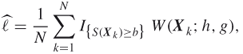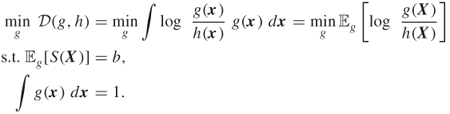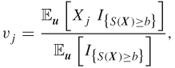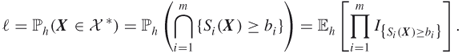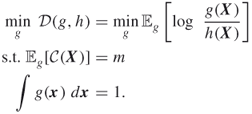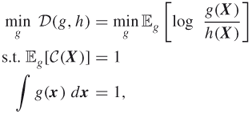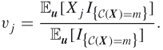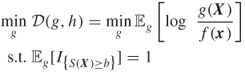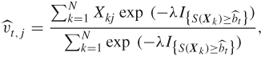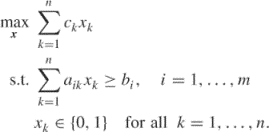Chapter 3
Minimum Cross-Entropy Method
This chapter deals with the minimum cross-entropy method, also known as the MinxEnt method for combinatorial optimization problems and rare-event probability estimation. The main idea of MinxEnt is to associate with each original optimization problem an auxiliary single-constrained convex optimization program in terms of probability density functions. The beauty is that this auxiliary program has a closed-form solution, which becomes the optimal zero variance solution, provided the “temperature” parameter is set to minus infinity. In addition, the associated pdf based on the product of marginals obtained from the joint optimal zero variance pdf coincide with the parametric pdf of the cross-entropy (CE) method. Thus, we obtain a strong connection between CE and MinxEnt, providing solid mathematical foundations.
3.1 Introduction
Let ![]() be a continuous function defined on some closed bounded
be a continuous function defined on some closed bounded ![]() -dimensional domain
-dimensional domain ![]() . Assume that
. Assume that ![]() is a unique minimum point over
is a unique minimum point over ![]() . The following theorem is due to Pincus [94].
. The following theorem is due to Pincus [94].
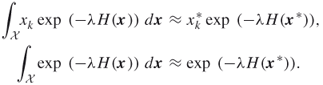
This is because, for large ![]() , the major contribution to the integrals appearing in (3.1) comes from a small neighborhood of the minimizer
, the major contribution to the integrals appearing in (3.1) comes from a small neighborhood of the minimizer ![]() .
.
Pincus' theorem holds for discrete optimization as well (assuming ![]() ). In this case, the integrals should be replaced by the relevant sums.
). In this case, the integrals should be replaced by the relevant sums.
There are many Monte Carlo methods for evaluating the coordinates of ![]() , that is, for approximating the ratio appearing in (3.1). Among them is the celebrated simulated annealing method, which is based on a Markov chain Monte Carlo technique, also called Metropolis' sampling procedure. The idea of the method is to sample from the Boltzmann density
, that is, for approximating the ratio appearing in (3.1). Among them is the celebrated simulated annealing method, which is based on a Markov chain Monte Carlo technique, also called Metropolis' sampling procedure. The idea of the method is to sample from the Boltzmann density
without resorting to calculation of the integral (the denumerator). For details see [108].
It is important to note that, in general, sampling from the complex multidimensional pdf ![]() is a formidable task. If, however, the function
is a formidable task. If, however, the function ![]() is separable, that is, it can be represented by
is separable, that is, it can be represented by
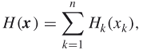
then the pdf ![]() in (3.2) decomposes as the product of its marginal pdfs, that is, it can be written as
in (3.2) decomposes as the product of its marginal pdfs, that is, it can be written as
3.3 ![]()
Clearly, for a decomposable function ![]() sampling from the one-dimensional marginal pdfs of
sampling from the one-dimensional marginal pdfs of ![]() is fast.
is fast.
Consider the application of the simulated annealing method to combinatorial optimization problems. As an example, consider the traveling salesman problem with ![]() cities. In this case, [1] shows how simulated annealing runs a Markov chain
cities. In this case, [1] shows how simulated annealing runs a Markov chain ![]() with
with ![]() states and
states and ![]() denoting the length of the tour. As
denoting the length of the tour. As ![]() the stationary distribution of
the stationary distribution of ![]() will become a degenerated one, that is, it converges to the optimal solution
will become a degenerated one, that is, it converges to the optimal solution ![]() (shortest tour in the case of traveling salesman problem). It can be proved [1] that, in the case of multiple solutions, say
(shortest tour in the case of traveling salesman problem). It can be proved [1] that, in the case of multiple solutions, say ![]() solutions, we have that as
solutions, we have that as ![]() the stationary distribution of
the stationary distribution of ![]() will be uniform on the set of the
will be uniform on the set of the ![]() optimal solutions.
optimal solutions.
The main drawback of simulated annealing is that it is slow and ![]() , called the annealing temperature, must be chosen heuristically.
, called the annealing temperature, must be chosen heuristically.
We present a different Monte Carlo method, which we call MinxEnt. It is also associated with the Boltzmann distribution, however, it is obtained by solving a MinxEnt program of a special type and is suitable for rare-event probability estimation and approximation of the optimal solutions of a broad class of NP-hard linear integer and combinatorial optimization problems.
The main idea of the MinxEnt approach is to associate with each original optimization problem an auxiliary single-constrained convex MinxEnt program of a special type, which has a closed form solution.
The rest of this chapter is organized as follows. In Section 3.2, we present some background on the classic MinxEnt program. In Section 3.3, we establish connections between rare-event probability estimation and MinxEnt, and present what is called the basic MinxEnt (BME). Section 3.4 presents a new MinxEnt method, which involves indicator functions and is called the indicator MinxEnt (IME). We prove that the optimal pdf obtained from the solution of the IME program is a zero variance one, provided the temperature parameter is set to minus infinity. This is quite a remarkable result. In addition, we prove that the parametric pdf based on the product of marginals obtained from the optimal zero-variance pdf coincides with the parametric pdf of the standard CE method, which we covered in the previous chapter. A remarkable consequence is that we obtain a strong mathematical foundation for CE. In Section 3.5 we present the IME algorithm for optimization.
3.2 Classic MinxEnt Method
The classic MinxEnt program reads as
Here, ![]() and
and ![]() are
are ![]() -dimensional pdfs;
-dimensional pdfs; ![]() are given functions; and
are given functions; and ![]() is an
is an ![]() -dimensional vector. Here,
-dimensional vector. Here, ![]() is assumed to be known and is called the prior pdf. The program (3.4) is called the classic minimum cross-entropy or simply the MinxEnt program. If the prior
is assumed to be known and is called the prior pdf. The program (3.4) is called the classic minimum cross-entropy or simply the MinxEnt program. If the prior ![]() is constant, then
is constant, then ![]() , so that the minimization of
, so that the minimization of ![]() in (3.4) can be replaced with the maximization of
in (3.4) can be replaced with the maximization of
where ![]() is the Shannon entropy [63]. The corresponding program is called the Jaynes' MinxEnt program. Note that the former minimizes the Kullback-Leibler cross-entropy, while the latter maximizes the Shannon entropy [63]. For a good paper on the generalization of MinxEnt, see [16].
is the Shannon entropy [63]. The corresponding program is called the Jaynes' MinxEnt program. Note that the former minimizes the Kullback-Leibler cross-entropy, while the latter maximizes the Shannon entropy [63]. For a good paper on the generalization of MinxEnt, see [16].
The MinxEnt program, which under mild conditions [8] presents a convex constrained functional optimization problem, can be solved via Lagrange multipliers. The solution is given by [8]
where ![]() are obtained from the solution of the following system of equations:
are obtained from the solution of the following system of equations:
The MinxEnt solution ![]() can be written as
can be written as
3.8 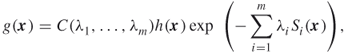
where
3.9 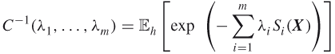
is the normalization constant.
In the particular case where each ![]() is coordinate-wise separable, that is,
is coordinate-wise separable, that is,
3.10 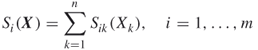
and the components ![]() of the random vector
of the random vector ![]() are independent. The joint pdf
are independent. The joint pdf ![]() in (3.6) reduces to the product of marginal pdfs. In such case, we say that
in (3.6) reduces to the product of marginal pdfs. In such case, we say that ![]() is decomposable.
is decomposable.
In particular, the ![]() -th component of
-th component of ![]() can be written as
can be written as
3.11 ![]()
coincides with the celebrated optimal exponential change of measure (ECM). Note that typically in a multidimensional ECM, one twists each component separately, using possibly different twisting parameters. In contrast, the optimal solution to the MinxEnt program is parameterized by a single-dimensional parameter ![]() , so for the multidimensional case ECM differs from MinxEnt.
, so for the multidimensional case ECM differs from MinxEnt.
The optimal parameter vector ![]() , derived from the solution of (3.13), can be written component-wise as
, derived from the solution of (3.13), can be written component-wise as
3.14 ![]()
where ![]() is derived from the numerical solution of
is derived from the numerical solution of
3.15 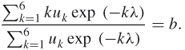
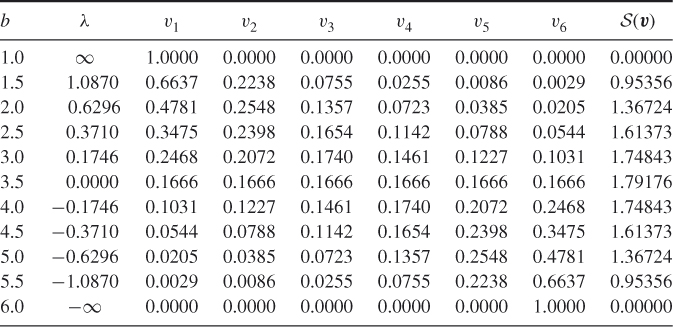
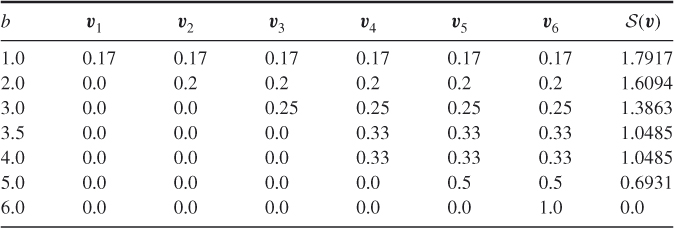
Table 3.1, which is an exact replica of Table 4.1 of [63], presents ![]() ,
, ![]() , and the entropy
, and the entropy ![]() as functions of
as functions of ![]() for a fair die, that is, with the prior
for a fair die, that is, with the prior ![]() . The table is self-explanatory.
. The table is self-explanatory.
- If
 , then
, then  and, thus,
and, thus, 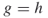 .
. 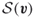 is strictly concave in
is strictly concave in 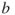 and the maximal entropy
and the maximal entropy 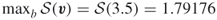 .
.- For the extreme values of
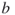 , that is, for
, that is, for 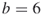 and
and 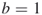 , the corresponding optimal solutions are
, the corresponding optimal solutions are 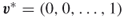 and
and 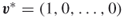 , respectively; that is, the pdf
, respectively; that is, the pdf 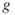 becomes degenerated. For these cases:
1. The entropy is
becomes degenerated. For these cases:
1. The entropy is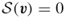 , and thus there is no uncertainty (for both degenerated vectors,
, and thus there is no uncertainty (for both degenerated vectors, 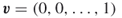 and
and 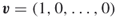 ).2. For
).2. For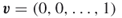 and
and 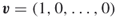 we have that
we have that 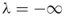 and
and 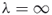 , respectively. This important observation is in the spirit of Pincus [94] Theorem 3.1 and will play an important role below.3. It can also be readily shown that
, respectively. This important observation is in the spirit of Pincus [94] Theorem 3.1 and will play an important role below.3. It can also be readily shown that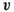 is degenerated regardless of the prior
is degenerated regardless of the prior 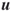 .
.
The above observations for the die example can be readily extended to the case where instead of ![]() one considers
one considers ![]() with
with ![]() and with arbitrary
and with arbitrary ![]() 's.
's.
3.16 ![]()
where ![]() are obtained from the solution of the following system of equations:
are obtained from the solution of the following system of equations:
3.17 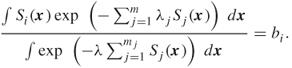
We extend next the MinxEnt program (3.4) to both equality and inequality constraints; that is, we consider the following general MinxEnt program:
In this case, applying the Kuhn-Tucker [75] conditions to the program (3.18) we readily obtain that ![]() remains the same as in (3.6), while
remains the same as in (3.6), while ![]() are found from the solution of the following convex program:
are found from the solution of the following convex program:
3.19 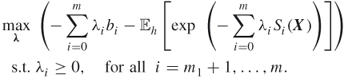
3.3 Rare Events and MinxEnt
To establish the connection between MinxEnt and rare events, we consider the problem of computing a rare-event probability of the form
Here, ![]() is a random vector with pdf
is a random vector with pdf ![]() ,
, ![]() is a performance function, and
is a performance function, and ![]() is such that
is such that ![]() is a rare event.
is a rare event.
Suppose that we estimate ![]() by the importance sampling estimator
by the importance sampling estimator
using the importance sampling pdf ![]() (see Section 2.2). Then the MinxEnt program that determines
(see Section 2.2). Then the MinxEnt program that determines ![]() has the following single-constrained formulation:
has the following single-constrained formulation:
The solution is (cf. (3.6))
and ![]() solves
solves
We call (3.22) and (3.23), (3.24) the basic MinxEnt (BME) program and solution, respectively. This is the nonparametric setting in which generally the solution ![]() is a difficult pdf to generate samples from. As a typical example, suppose that the prior
is a difficult pdf to generate samples from. As a typical example, suppose that the prior ![]() is the uniform pdf on a bounded state space
is the uniform pdf on a bounded state space ![]() , that is
, that is ![]() , where
, where ![]() denotes the total area of the set
denotes the total area of the set ![]() . The rare event is
. The rare event is ![]() . The importance sampling estimator (3.21) using the MinxEnt solution (3.23) becomes
. The importance sampling estimator (3.21) using the MinxEnt solution (3.23) becomes
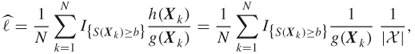
where ![]() is a random sample from
is a random sample from ![]() .
.
We give two simple examples; the first one leads to a simple simulation procedure from ![]() , the second one does not.
, the second one does not.
![]()
where ![]() and
and ![]() are independent uniform
are independent uniform ![]() random variables. Thus,
random variables. Thus,
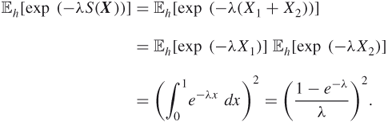
The parameter ![]() solves
solves
![]()
![]()
on ![]() , otherwise
, otherwise ![]() . Hence, under the importance sampling pdf
. Hence, under the importance sampling pdf ![]() ,
, ![]() and
and ![]() are again independent but have a conditional exponential distribution with parameter
are again independent but have a conditional exponential distribution with parameter ![]() , conditioned on
, conditioned on ![]() . Generating samples from
. Generating samples from ![]() is straightforward.
is straightforward.![]()
![]()
where ![]() is the circle segment above the chord
is the circle segment above the chord ![]() . Clearly,
. Clearly, ![]() when
when ![]() . Note that
. Note that ![]() and
and ![]() are dependent. Generating samples from
are dependent. Generating samples from ![]() is easy and can be done, for example, by acceptance-rejection from uniform samples in the square
is easy and can be done, for example, by acceptance-rejection from uniform samples in the square ![]() . In this example we get explicit expressions neither for the normalizing constant
. In this example we get explicit expressions neither for the normalizing constant ![]() nor for the importance sampling pdf
nor for the importance sampling pdf ![]() .
.![]()
As we already mentioned in Chapter 2, the cross-entropy method assumes that the prior pdf ![]() belongs to a parameterized family
belongs to a parameterized family ![]() of pdfs (2.6), where
of pdfs (2.6), where ![]() is called the nominal parameter vector. The solution
is called the nominal parameter vector. The solution ![]() to the MinxEnt program as given in (3.23) is generally not a pdf in that parameterized family. In some cases it is possible to find an approximate pdf
to the MinxEnt program as given in (3.23) is generally not a pdf in that parameterized family. In some cases it is possible to find an approximate pdf ![]() as in the following setting.
as in the following setting.
Let ![]()
![]() be the prior pdf. The MinxEnt solution for
be the prior pdf. The MinxEnt solution for ![]() is
is
Suppose that the family ![]() satisfies the marginal expectation parameterization, and let
satisfies the marginal expectation parameterization, and let ![]() be any parameter vector for the family
be any parameter vector for the family ![]() . Then the above analysis suggests carrying out the importance sampling using
. Then the above analysis suggests carrying out the importance sampling using ![]() equal to
equal to ![]() given in (3.25). Hence, we approximate the MinxEnt solution
given in (3.25). Hence, we approximate the MinxEnt solution ![]() by
by ![]() with
with
Note that formula (3.26) is similar to the corresponding cross-entropy solution [107]
with one main difference: the indicator function ![]() in the CE formula is replaced by
in the CE formula is replaced by ![]() .
.
![]()
In other words,
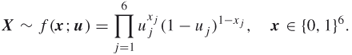
Assume further that the performance function is ![]() , and we want to find the optimal parameter
, and we want to find the optimal parameter ![]() to calculate the probability of the event
to calculate the probability of the event ![]() .
.
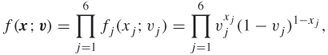
with
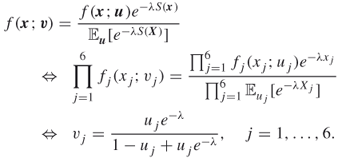
The parameter ![]() is obtained by solving
is obtained by solving
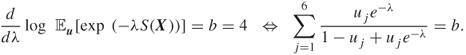
![]()
![]()
The gain is
![]()
![]()
3.4 Indicator MinxEnt Method
Consider the set
where ![]() are arbitrary functions. As before, we assume that the random variable
are arbitrary functions. As before, we assume that the random variable ![]() is distributed according to a prior pdf
is distributed according to a prior pdf ![]() .
.
Hence, we associate with (3.28) the following multiple-event probability:
Note that (3.29) extends (3.20) in the sense that it involves simultaneously an intersection of ![]() events
events ![]() , that is, multiple events rather than a single one
, that is, multiple events rather than a single one ![]() . Note also that some of the constraints may be equality ones, that is,
. Note also that some of the constraints may be equality ones, that is, ![]() . Note finally that (3.29) has some interesting applications in rare-event simulation. For example, in a queueing model one might be interested in estimating the probability of the simultaneous occurrence of two events,
. Note finally that (3.29) has some interesting applications in rare-event simulation. For example, in a queueing model one might be interested in estimating the probability of the simultaneous occurrence of two events, ![]() and
and ![]() , where the first is associated with buffer overflow (the number of customers
, where the first is associated with buffer overflow (the number of customers ![]() is at least
is at least ![]() ), and the second is associated with the sojourn time (the waiting time of the customers
), and the second is associated with the sojourn time (the waiting time of the customers ![]() in the queueing system is at least
in the queueing system is at least ![]() ).
).
We assume that each individual event ![]() , is not rare, that is each probability
, is not rare, that is each probability ![]() is not a rare-event probability, say
is not a rare-event probability, say ![]() but their intersection forms a rare-event probability
but their intersection forms a rare-event probability ![]() . Similar to the single-event case in (3.20) we are interested in efficient estimation of
. Similar to the single-event case in (3.20) we are interested in efficient estimation of ![]() defined in (3.29).
defined in (3.29).
The main idea of the indicator MinxEnt approach is to design an importance sampling pdf ![]() such that under
such that under ![]() all constraints
all constraints ![]() are fulfilled with certainty. For that purpose, we define
are fulfilled with certainty. For that purpose, we define
3.30 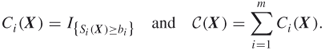
Then the indicator MinxEnt program is defined by the following single-constrained MinxEnt program
Its solution ![]() (see Section 3.2) is
(see Section 3.2) is
where ![]() is obtained from the solution of the following equation:
is obtained from the solution of the following equation:
We call (3.31) and (3.32), (3.33) the indicator MinxEnt (IME) program and solution, respectively.
When (3.33) has no solution, then, in fact, the set ![]() is empty.
is empty.
We will use ![]() to estimate the rare-event probability
to estimate the rare-event probability ![]() given in (3.29). In forthcoming Lemmas 3.1 and 3.2 we will show that
given in (3.29). In forthcoming Lemmas 3.1 and 3.2 we will show that ![]() coincides with the zero-variance optimal importance sampling pdf, that is, with
coincides with the zero-variance optimal importance sampling pdf, that is, with
Specifically, this gives
3.35 ![]()
Note that the classic multiconstrained MinxEnt program (3.4) involves expectations of ![]() , while the proposed single-constrained one (3.31) is based on the expectations of the indicators of
, while the proposed single-constrained one (3.31) is based on the expectations of the indicators of ![]() , so the name indicator MinxEnt program or simply IME program.
, so the name indicator MinxEnt program or simply IME program.
For ![]() the IME program (3.31) reduces to
the IME program (3.31) reduces to
where ![]() .
.
Observe also that, in this case, the single-constrained programs (3.36) and (3.22) do not coincide: in the former case we use an expectation of the indicator of ![]() , that is,
, that is, ![]() , while in the latter case we use an expectation of
, while in the latter case we use an expectation of ![]() , that is,
, that is, ![]() . We shall treat the program (3.36) in more details in Section 3.5.
. We shall treat the program (3.36) in more details in Section 3.5.
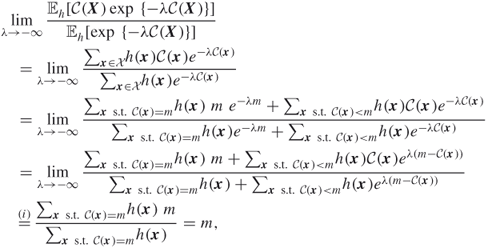
where we used in equality (i) that ![]() when
when ![]() because
because ![]() .
.![]()
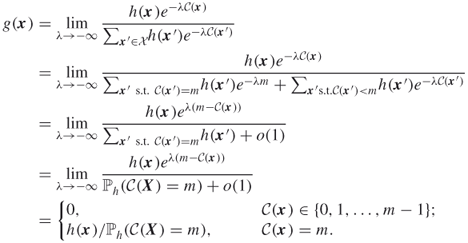
![]()
Observe again that generating samples from a multidimensional Boltzmann pdf, like ![]() in (3.32), is a difficult task. One might apply Markov chain Monte Carlo algorithms [108], but these are time consuming.
in (3.32), is a difficult task. One might apply Markov chain Monte Carlo algorithms [108], but these are time consuming.
Assume further that the prior ![]() is given as a parameterized pdf
is given as a parameterized pdf ![]() . Then, similar to [103], we shall approximate
. Then, similar to [103], we shall approximate ![]() in (3.32) by a product of the marginal pdfs of a parameterized pdf
in (3.32) by a product of the marginal pdfs of a parameterized pdf ![]() . That is,
. That is, ![]() , with
, with
which coincides with (3.26) up to the notations. A further restriction assumes that each component of ![]() is discrete random variable on
is discrete random variable on ![]() . Then (3.37) extends to
. Then (3.37) extends to
3.38 ![]()
3.4.1 Connection between CE and IME
To establish the connection between CE and IME we need the following result:
Theorem 3.2 is crucial for the foundations of the CE method. Indeed, designed originally in [101] as a heuristics for rare-event estimation and combinatorial optimization problems, Theorem 3.2 states that CE has strong connections with the IME program (3.31). The main reason is that the optimal parametric pdf ![]() (with
(with ![]() in (3.37) and
in (3.37) and ![]() ) and the CE pdf (with
) and the CE pdf (with ![]() as in (3.39)) obtained heuristically from the solution of the following cross-entropy program:
as in (3.39)) obtained heuristically from the solution of the following cross-entropy program:
![]()
are the same, provided ![]() is the zero variance IS pdf.
is the zero variance IS pdf.
The crucial difference between the proposed IME method and its CE counterparts lies in their simulation-based versions: in the latter we always require to generate a sequence of tuples ![]() , while in the former we can fix in advance the temperature parameter
, while in the former we can fix in advance the temperature parameter ![]() (to be set a large negative number) and then generate a sequence of parameter vectors
(to be set a large negative number) and then generate a sequence of parameter vectors ![]() based on (3.37) alone. In addition, in contrast to CE, neither the elite sample nor the rarity parameter are involved in IME. As result, the proposed IME Algorithm becomes typically simpler, faster and at least as accurate as the standard CE based on (3.39).
based on (3.37) alone. In addition, in contrast to CE, neither the elite sample nor the rarity parameter are involved in IME. As result, the proposed IME Algorithm becomes typically simpler, faster and at least as accurate as the standard CE based on (3.39).
3.5 IME Method for Combinatorial Optimization
We consider here unconstrained and constrained optimization, respectively.
3.5.1 Unconstrained Combinatorial Optimization
Consider the following non-smooth (continuous or discrete) unconstrained optimization program:
![]()
Before proceeding with optimization recall that
If not stated otherwise, we shall use the indicator MinxEnt.
To proceed with ![]() , denote by
, denote by ![]() the optimal function value. In this case, the indicator MinxEnt program becomes
the optimal function value. In this case, the indicator MinxEnt program becomes
![]()
The corresponding updating of the component of the vector ![]() can be written as
can be written as
where ![]() is a big negative number.
is a big negative number.
To motivate the program (3.40), consider again the die rolling example.
3.42 ![]()
As a stopping criterion one can use, for example, the following: if for some ![]() , say
, say ![]()
3.43 ![]()
then stop.
3.5.2 Constrained Combinatorial Optimization: The Penalty Function Approach
Consider the following constrained combinatorial optimization problem (with inequality constraints):
Assume in addition that the vector ![]() is binary and all components
is binary and all components ![]() and
and ![]() are positive numbers. Using the penalty method approach we can reduce the original constraint problem (3.44) to the following unconstrained one
are positive numbers. Using the penalty method approach we can reduce the original constraint problem (3.44) to the following unconstrained one
3.45 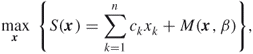
where the penalty function is defined as
3.46 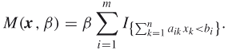
Here,
3.47 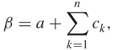
where ![]() is a positive number. If not stated otherwise, we assume that
is a positive number. If not stated otherwise, we assume that ![]() . Note that
. Note that ![]() is an increasing function of the number of the constraints that
is an increasing function of the number of the constraints that ![]() satisfies and the penalty parameter
satisfies and the penalty parameter ![]() is chosen such that
is chosen such that ![]() is negative when and only when at least one of the constraints is not satisfied. If
is negative when and only when at least one of the constraints is not satisfied. If ![]() satisfies all the constraints in (3.44), then
satisfies all the constraints in (3.44), then ![]() and the
and the ![]() value is equal to the value of the original performance function in (3.44). Clearly, the optimization program (3.44) can again be associated with the rare-event probability estimation problem, where
value is equal to the value of the original performance function in (3.44). Clearly, the optimization program (3.44) can again be associated with the rare-event probability estimation problem, where ![]() is a vector of iid
is a vector of iid ![]() components.
components.
We found that our numerical results with MinxEnt Algorithm 3.1 for different unconstrained and constrained combinatorial optimization problems show that it is comparable with its counterpart CE in both accuracy and the CPU time.