Chapter 9

Variation

9.1 Variation and Uncertainty

Variation often gives rise to uncertainty. Though we can recognize a group of objects called teapots, the variation present from one teapot to another results in our being uncertain whether we shall spill some of the tea when first pouring from a strange pot, for some pots are good pourers, some are not. More seriously, all biological material exhibits variation; even the simple influenza virus varies, with the consequence that we are uncertain what vaccine to use against it. Human beings show variation that we rightly cherish, yet it gives rise to uncertainty, whether in what size of trousers a retailer should stock, or in a stranger's reaction to a request.

There are only a few topics where variation is not present. Precision engineering is capable of making objects, like the balls in the urn, that are, for practical purposes, indistinguishable and portray no obvious variation. One atom of an isotope of hydrogen is regarded as the same as any other atom and the behavior of the isotope in the presence of oxygen can be predicted perfectly. We can say, in the spirit of §7.3, that one atom can be exchanged for another. Physics and chemistry are both founded on this lack of variation that partly explains why physical scientists were so uncomfortable with quantum physics and its unpredictability. It also helps to explain why those two subjects have advanced more than others, like biology, because they are not hampered by variation and so have less uncertainty. Biology is now advancing more quickly since some aspects of it have been reduced to the chemistry of amino acids. However, the laws of genetics contain randomness and the resulting variation is basic to the concept of evolution, where variants more suited to their environment stand a better chance of producing offspring that survive and breed.

Variation produces uncertainty because you cannot be sure what the variable material will do. Uncertainty inevitably necessitates description in terms of probability, hence probability is an essential tool in the handling of variation. This chapter is devoted to a study of variation and probability, beginning with a simple example, the familiar balls in an urn. Before doing so, we need to look at the rule of the extension of the conversation again because it plays a key role in the analysis and provides another form of Bayes rule. In equation (5.7) of §5.6, the rule was presented as extending from one event E to include another event F, with its complement F ^c; and in §8.1 it was mentioned that, just as the basic rules applied to any number of events, not just two, so would the extension rule. It is the precise form of this that needs to be discussed. Consider events , which are exclusive (§5.2) in that at most one of them can be true, and also exhaustive, in that one of them must be true, or they exhaust the possibilities; they are said to form a partition of the events. Clearly the original pair, F and F ^c, form a partition. Consider the events . They are exclusive but do not exhaust the possibilities since E ^c might be true. What they do exhaust is E since they describe all the ways that E might occur. By the addition rule, Equation (8.2) of §8.1, for n events,

(9.1)

In words, if the events F_i form a partition, p (E) is equal to the sum of n terms of which a typical one is p (EF_i ). By the product rule, , so the general form for the rule of the extension of the conversation is as follows:

If, on some knowledge base, events form a partition and E is another event, p (E) is equal to the sum of n terms, of which a typical one is . It is this form that will be repeatedly used in the rest of the book.

Bayes rule, applied separately to each member of the partition, and omitting reference to the knowledge base, says

In words, your prior is multiplied by your likelihood and divided by , your probability of obtaining evidence E. This last term is difficult to think about but can be obtained from the prior and likelihood by use of the extension of the conversation from E to include the partition (9.1). It is this form of Bayes rule that is commonly used in statistics (Chapter 14). There is an equivalent way of approaching this form. For each , is the product of the prior and the likelihood, divided by the same term, for each i. But we know the must add to one since the form a partition. So if all the products are added, the result may be divided by some value to make the total one. Clearly this total is just that given by the extension of the conversation (9.1). Bayes rule can therefore be expressed by saying

where the symbol means “is proportional to”. This form is especially attractive because it clearly demonstrates that your posterior probabilities depend on your likelihood and your prior, and on nothing else.

9.2 Binomial Distribution

Take our usual urn containing a vast number of balls, identical except that a known proportion are colored red, the rest white, and suppose you take one ball at random, then your probability that it will be red is . Generally, if you take n balls from the urn at random, you will have a Bernoulli series (§7.4) in which the withdrawals are exchangeable and your probability for any outcome of the n drawings depends, not on the order of red and white balls, but only on the number, say r, of red balls out of the n. Even with and n fixed, the number r of red balls will be variable and uncertain. We now calculate your probability of r red balls, given n and , which, in the standard notation, is , the presence of after the vertical line reminding us that is supposed known, as well as n. There is also an unstated knowledge base, which incorporates things like the withdrawals being random. Take an example of drawing 6 balls from the urn and determine your probability of just one red, and therefore 5 white balls; n = 6, r = 1. One way this can happen is to have the red ball appear first, followed by the 5 white, with probability by the multiplication rule for the random (and therefore independent) drawings, as in §7.4. There are 6 such possibilities, for the single red can appear in any of 6 positions, and each has the same probability, so by the addition rule. This method works for any values of r and n. The product is obvious, but the number of ways of obtaining r red in n drawings is a little tricky, so will be omitted.

Here is a numerical example with and n = 6. Your probabilities are given to two significant figures; that is, two digits after the 0's, if any, that follow the decimal point (§2.9).

Thus your probability of 1 red ball, when 6 are drawn from an urn with one third of the balls red, is 0.26, as the reader can verify by putting in the expression . The table shows that 1, 2, or 3 red balls are each quite probable but 0, 4, or 5 are somewhat unusual and having every ball red, r = 6, is most surprising. The numbers here reflect your uncertainty when 6 balls are removed randomly from the urn, but if you were repeatedly to remove 6 and recognize the connection between these ideas and frequency expressed in the law of large numbers (§7.6), then, in the long run, you would have exactly 2 red out of the 6 in 33%, or one third, of the time. Here we have variation, one drawing of 6 balls typically differing from the result of another 6, so that the variation and the uncertainty are intimately related.

A useful way of looking at this situation, which generalizes to many others, is to note that there are 7 exclusive events in the table, which exhaust the possibilities and so form a partition. They may be written E₀, E₁ up to E₆, where E_r corresponds to r red balls; thus, from the table . The 7 probabilities add to 1 (apart from rounding errors) and we say the total probability of 1 is distributed over the 7 values that form the partition. Generally, if there are a finite number of events, which are exclusive (only one can be true) and exhaustive (one must be true), then the corresponding set of probabilities is said to form a probability distribution. Since this is a book about probability, we shall typically drop the adjective and refer to a distribution. The distribution tabulated above is an example of a binomial distribution that applies whenever there is a fixed number, here 6, of observations, each of which can result in an event being true or false (red or white). The chance (§7.8) of truth is the same for each observation (here θ = 1/3) and the events are independent. The binomial distribution relates to a Bernoulli series (§7.4) where the exchangeable property reduces consideration to the number of true events, not their order. The number of observations, n, is termed the index of the binomial and the chance of truth (red), θ, is called the parameter. The distribution tabulated above has index 6 and parameter 1/3. The variation in the number of red balls, when a fixed number of balls is withdrawn, is described by the binomial distribution.

The number r of red balls can take any value from 0 to n inclusive, with probabilities p (r) for you, omitting the conditions from the notation. The idea generalizes to every quantity that can take a finite number of possible values with probabilities assigned by you to each value. Such a quantity is called an uncertain quantity. Thus the number of red balls is an uncertain quantity and the probabilities form your distribution of that quantity. (The term random variable often replaces uncertain quantity.) An event can be considered as an uncertain quantity taking two values, 1, true and 0, false, so that an uncertain quantity is a generalization of an uncertain event and its distribution generalizes the probability of an event. Most of the examples considered in Chapter 1 concern uncertain quantities or can easily be extended to do so. Thus the uncertain event of “rain tomorrow” can be extended to “millimeters of rain tomorrow” (Example 1 of §1.2) or the event of “ace” to the number on the card (Example 7). The amount of inflation (Example 10) or the proportion of HIV (Example 11) are examples of quantities which are uncertain.

The binomial distribution is relevant to many practical situations. If you observe a number n of people taken at random, called a sample of people, then r, the number of women, will have a binomial distribution with index n and parameter θ = , or slightly less than if the sample is of babies, or more than if it is of persons more than 80 years of age. If, for the same people, the gene with alleles A or a, with A dominant, were investigated, then the number r of double recessives aa, often those with a defect, will be binomial with parameter , where θ is the proportion of alleles a in the population from which the sample was taken. If n observations are made of the fall of a ball in roulette, played in a reputable casino, then r, the number of balls falling in slot 22, is binomial with index n and parameter θ = 137 if there are 37 slots. Notice that in these examples three requirements for the binomial are satisfied: the number n is fixed, the individual occurrences are random, and you have the same, known probability θ of the outcome under consideration (sex, defective or 22) for each occurrence. A more common situation is where these conditions obtain except that θ is unknown to you and is a chance, about which you have a probability distribution. As an example, consider the case at the beginning of this paragraph when sex is replaced by voting intent, with only two candidates and the “don't knows” omitted. Then θ is unknown and you can apply Bayes rule to modify your opinion of it after hearing the intentions of the voters. Notice that the samples must be taken at random to preserve exchangeability. It would not be correct to ask all members of a household since there exists a tendency for members to be in agreement within households.

Although we shall not explore the point in any detail, it is worth noting why n is fixed in this, and other, examples. Suppose the balls were taken from the urn until you had two red balls in succession, and then stopped. There would be a distribution for the total number of red balls withdrawn but it would be different from the binomial obtained when the number of withdrawn balls was fixed. For example, your probability of finishing with one red ball is zero, compared with 0.26 in our binomial example with n = 6. It is not unknown for people to sample until they reach a situation that is favorable to them, two consecutive reds in our example. It is then incorrect to treat the sample as binomial. On the other hand, a useful practice in medical trials is to stop when the evidence is thought enough to establish the merit, or inadequacy, of the drug under test. This is permissible provided the correct probability is used. The point is treated in more detail under the term “optional stopping” in §14.3.

9.3 Expectation

A distribution for an uncertain quantity is a rather complicated affair, even in the binomial case with n = 6 it consists of 7 numbers, adding to one, and it would be desirable to encapsulate the main features of a distribution in far fewer numbers. In doing this, some knowledge of the distribution will be lost, but there will be an increase in understanding. In this section the most important feature of an uncertain quantity and your distribution for it will be developed. Again we resort to our familiar urn, but it will be used somewhat differently from the last section and to emphasize the difference, and hopefully prevent confusion, a slight change in notation will be employed.

Consider an urn containing a known number m of balls, identical except for the fact that s of them are scarlet, the rest white. If s is unknown to you, it is an uncertain quantity and you will have a distribution for it, p (s), being your probability that the number of scarlet balls is s. Suppose that one ball is to be drawn at random from the urn and denote by S the event that it is scarlet. What is your probability for this when s is uncertain? (There is an unstated knowledge base that includes m, the total number of balls in the urn.) If the number of scarlet balls in the urn were known to you, the answer would be simple from the basic definition of probability in §3.3, . This suggests that it might be worthwhile extending the conversation from S to include s. Using the general form at the end of §9.1 to calculate p (S) it is necessary to evaluate the products for each value of s and add over all values of s from 0 to m. Since , the products to be added reduce to sp (s) and their sum has to be divided by m. The sum of the products sp (s) is called your expectation of the uncertain quantity s and will be denoted by E and not confused with the use of E for an event, or for evidence. Often E is called the expected value of s. Generally, for any distribution of an unknown quantity, the result of taking the probability of any value of the quantity, multiplying it by the value, and adding all the products, is called the expectation of the uncertain quantity. Since every distribution can be conceptually associated with the random withdrawal of a ball from an urn, in the manner employed here, the idea is of wide applicability. Part of its importance lies in the fact that if the quantity, s, is known, your probability for the scarlet ball is s m, whereas when unknown, it is E m, replacing the unknown value s by the known expectation E. As far as the random withdrawal of one ball is concerned, the uncertain state of the urn can be replaced by an urn with a known number E of scarlet balls. When we discuss decision analysis in §10.4, we encounter another case where uncertainty can be replaced by expectation without any loss of power. Of course, some features of a distribution are lost if only expectation is employed, but it is far and away the most important feature of a distribution, or of the quantity to which it relates. In many cases, as with the urn, it provides all the information you need. So important is it that other names are in use. It is sometimes called your prevision of the uncertain quantity, your vision of it before determining its true value. When referring to a distribution, without having any particular quantity in mind, it is often called the mean of the distribution. The same term is frequently used for the quantity, thus we talk about the mean income or the mean size of family.

The connection between probability and expectation is even closer than the development just given suggests. We saw in §9.2 that one could associate any event A with a quantity taking the value zero if A is false, and one if true, these being the appropriate limits of your probability for A. What is your expectation of this quantity? Recall we have to take each value of the quantity, multiply by its probability, and add the resulting products. Here

so that your expectation and your probability are identical. Some writers have based their whole treatment of uncertainty on expectation, rather than on probability. This is entirely satisfactory, but we have chosen not to adopt that approach for three reasons:

1. It can happen that the quantity can take so many values that the sum of all the products becomes unwieldy. This is essentially a mathematical reason and, in that language, the sum diverges.

2. We have seen that it is often hard to assess probability (§§3.5 and 5.6). It is even harder to assess expectation since a quantity can assume so many values, whereas probability is just expectation for a quantity that can only assume two, 0 and 1.

3. Expectation can be more easily misunderstood than probability. Suppose a standard die is sensibly rolled, then you will ordinarily associate probability 16 with each of the possible values 1, 2, 3, 4, 5, 6 for the number of spots that might appear uppermost when the die comes to rest, and hence have expectation (1 + 2 + 3 + 4 + 5 + 6)/6 = 3. Yet in the ordinary use of the English language, you will never “expect” to see 3 spots because it is impossible. However, if you were to receive $1 for every spot you would reasonably expect to receive $3. I once experienced communication problems with an official because I had said 2 defectives were expected in a batch of 100 components. He was never convinced and went around his department joking about the statistician who was half defective.

There is an alternative interpretation of expectation but this is left until another distribution has been discussed in §9.4. Notice that the concept of expectation, as presented here, is not just a convenient quantity but arises naturally from a probability rule, namely the extension of the conversation. Also its derivation has nothing to do with frequency, the ball being withdrawn only once. Compare the comments in the final paragraph of §3.4.

9.4 Poisson Distribution

Suppose you are a telephone operator who handles calls for an emergency service and are beginning a tour of duty of 2 hours. You will be uncertain about the number of calls you will have to deal with during the tour and will therefore have a probability distribution for that number as an uncertain quantity. Table 9.1 gives a possible distribution.

Table 9.1 Poisson distribution with expectation 4.

For example, your probability of just 4 calls is 0.20, which can also be interpreted by considerations of frequency in §7.6 as meaning that, over a long sequence of tours, when conditions remain stable, you can anticipate 4 calls on about 20% of tours. Notice that more than 10 calls (>10) is thought to be a very rare event and all values above 10 have been lumped together. Again the probabilities add to 1 and they can be partially added, for example, your probability of eight or more calls, a busy tour, is 0.030 + 0.013 + 0.0053 + 0.0028 = 0.051, or roughly 1 in 20 tours are anticipated to be busy.

The tabulated distribution has been derived from two assumptions:

The first assumption says roughly that the demands for the emergency service are constant, and the second that what has happened so far in your tour does not affect the future. Notice that the assumptions are similar to those for the binomial distribution, the constancy of and the random withdrawals. In practice, neither of the assumptions may be exactly true, but experience has shown that small departures do not seriously affect the conclusions and that larger departures can be handled by building on cases where they do, rather as exchangeable series can be built on the Bernoulli form (§7.5). As a result, the ideas presented here are basic to many processes occurring naturally.

A distribution resulting from the assumptions is called a Poisson distribution, after a French mathematician of that name, and depends on only one value, the chance mentioned in the first assumption, called the parameter of the Poisson. The tabulation above is for the case where the chance is about 16. Notice that, in the description of the parameter, the unit, here 5 minutes, is vital, for 1 minute the parameter would be about 130, a fifth of the previous value.

There is an alternative parametric description of the Poisson distribution that is often more convenient and uses the expectation, or mean, of the distribution. For that just tabulated, the expectation is

where the dots signify that the values from 3 to 9 calls have to be included and where values in excess of 10 have been replaced by 11. A simple exercise on a calculator shows that the sum is 4.03. Because the probabilities have been given only to two significant figures and that all values in excess of 10 have been put together, this result is not exact and the correct value is exactly 4. The tabulation above is for a mean of four calls in a 2 hour period. It is intuitively obvious and can be rigorously proved that if you expect 4 calls in 2 hours, you expect 1 in an hour and 16 in the 5 minute period above. Recall comment 3 in §9.3.

The Poisson distribution, or a close approximation to it, occurs very frequently in practice. It is a good approximation whenever there is a very small chance of an event occurring, but lots of opportunities when it might occur, and where one happening does not interfere with another. There are lots of 1 minute periods when a call might be received but a very small chance of one in any such period. In the example, 120 such periods each with chance about 4120 = 130. There is little chance of your falling ill but there are lots of people who could fall ill, so illnesses in a population often satisfy a Poisson distribution. An example of this appears in §9.10. Historically, an early instance was deaths from the kick of a horse in the Prussian cavalry, where there were lots of soldiers interacting with horses, providing many opportunities for, but few casualties from, horse kicks. Indeed, the Poisson distribution is so ubiquitous that any departure from it gives rise to suspicions that something is amiss. Childhood deaths from leukemia near nuclear power plants provides an example, clusters of cases suggesting departure from the Poisson assumptions.

There is another way of thinking about the Poisson distribution that sheds further light on what is happening. To see this, suppose you are the operator on your shift of 2 hours, expecting 4 calls, and suppose, instead of fixing the duration and seeing how many calls arise, you think about the next call and wait to see how much time elapses before it occurs. You might query whether there is time for a cup of coffee before the phone rings. The second of the two assumptions above means that at any time, say 3.45, what has happened before then does not affect your uncertainty about the future, so forget the past and at 3.45 wait until the next call comes. Will you have to wait 1 minute, 2 minutes, or more? The number of minutes is, for you, an uncertain quantity and you will have a distribution for it. What can be said about this distribution? Common sense suggests that if you expect to receive 4 calls in 2 hours, you expect to wait half an hour for that one call. Here is a case where common sense is correct and generally if you expect C calls in an hour, you expect to wait 1C hours for the first one. But now look at the situation in a different way and ask what is the most probable time, to the nearest minute, that you will need to wait for that call? Will it be 1 minute, 2 minutes, or perhaps 30 minutes, the expected time? The answer surprises most people for it is 1 minute. As the time increases, the probability of your having to wait until then decreases, so that, in particular, the expected time has small probability. Here is an example where, for most people, common sense fails and our basic idea of coherence provides a different answer, an answer that stands up to rigorous scrutiny. The incorrect, common sense has led to the belief that the calls should be spread out somewhat uniformly, rather than occurring in clusters. In fact, even in a Poisson distribution, clusters often arise simply because small intervals between calls are more probable than large ones. This clustering has led to a popular tradition that events occur in threes; a tradition that comes about because of your large probabilities for small intervals. Clusters are natural and it does not require a special explanation to appreciate them. This is why it is hard to separate real clusters from the ones that occur solely from the Poisson distribution, as with leukemia mentioned in the last paragraph.

There is another interpretation for expectation that deserves notice. In your role as an operator, coming on duty at 16.00, you can expect 4 calls before you have a break at 18.00. Instead of just one specific tour of duty, suppose you are employed over a long period and accumulate 1000 tours. You expect 4000 calls in all and, in an extension of the law of large numbers in §7.6, you will actually experience something very close to 4000. In other words, the expectation of 4 is a long-term average. This interpretation is not as useful as the earlier one, referring to a specific tour, because it requires not just stability over 2, but over 2000 hours. It also confuses probability as belief with frequency, a confusion, which, as we saw in §7.2, is often misleading.

9.5 Spread

Your expectation of an uncertain quantity says something about what you anticipate or, in the frequency interpretation, tells you what might happen on the average. But there is another important feature of an uncertain quantity and that is its variation, referring to the departure, or spread, of individual results from your expectation. A simple way of appreciating the variation is to suppose the uncertain quantity is observed twice; for example, take the 6 balls from the urn as in §9.2 and observe the number of red balls; then repeat with a further 6. It will be rare that you obtain the same number of red balls on both occasions, the difference providing a measure of the variation, or spread. The operator experiencing two tours of duty will rarely have the same number of calls in the first as in the second. Exactly how the difference is turned into a measure of spread, or how it is employed when there are several observations, not just two, is an issue that is too technical for us to pursue here. The measure of spread ordinarily used is called the standard deviation. It is discussed further in §9.9. Instead we concentrate on a result that requires no technical skill beyond the appreciation of a square root. Recall (§2.9) that the square root of a number m is that number, written √m or , which, when multiplied by itself, √m × √m is equal to m. Thus the square root of 9 is 3 since 3 × 3 = 9. Of course, typical square roots are not integers or even simple fractions, a result that caused much distress in classical Greece, so that √2, for example, is about 1.41.

Let us return to making several observations on an uncertain quantity, in the last paragraph we took just two. Throughout the treatment that follows it is supposed that the observations obey two conditions:

These are similar to the conditions that, in a different context, lead to the Poisson distribution. In the case of 6 balls drawn from the urn, condition (1) means the constitution of the urn remains fixed and your selection continues to be random. (2) demands that you do not allow the result of the first draw to affect the second. In the Poisson case with the emergency service, the second tour of duty is not influenced by the first, as might happen were there to be a serious fire extending over both tours.

Under these conditions, let x and y be two observations of the uncertain quantity. Then, as already suggested, the difference x − y tells us something about the spread, whereas x + y reflects the total behavior. Clearly the latter has more spread than x or y. Thus, with the urn, the total number of red balls from two sets of 6 can vary between 0 and 12, rather than 0 to 6 for a single observation. The key question is how much does the spread increase in passing from x to x + y ? The answer is that for any reasonable measure, including the one hinted at above, but not developed for technical reasons, the spread is multiplied by √2. This is a special case of the square-root rule, which says that if m observations are made, under conditions (1) and (2), then the spread of the total of those observations is √m times that of each individual observation. The example had m = 2. The important feature here is that the variability of the total of m observations is not m times that of any one, but only √m times. √m is much smaller than m; for example, √25 is only 5.

The square-root rule is often presented in a slightly different way which agrees more with intuition. When we study science in §11.11, we will see that a basic tenet of the scientific method is the ability to repeat experiments. If the experiments obey the conditions above as they often do, then scientists will sensibly take the average of the observations in each of the m experiments, in preference to a single one. The average is the total divided by m, and since the spread of the total is √m times that of a single observation, the spread of the average must be √m, divided by m, or that of one observation divided by . ( since ). Thus the square-root rule says that the variation of the average is that of one observation divided by √m, so the scientists' use of repetition is effective in reducing variation, dividing it by √m. In this form, the square-root rule was, for many years, regarded by some experimental scientists as almost the only thing they needed to know about uncertainty. Although this is no longer true, it remains central to an understanding of variability. If 16 observations of the same quantity are made, the variability, or spread of the average is only one quarter that of a single observation.

The occurrence of the square root explains a phenomenon that we all experience when repetitions of an activity can be less interesting than doing it for the first time and ultimately can sometimes become of no interest at all. To divide the variation by 2, we need 4 repetitions; to divide it by 2 again, dividing by 4 in all, we need 16 repetitions so that the second halving in variation requires 12 = 16 − 4 repetitions rather than the 4 required first time. It expresses a law of diminishing returns, observation 16 having much less effect than observation 2. The square-root rule is not universal for, as we have emphasized, it requires independent and identical repetitions; but it does occur frequently and is very useful.

Although the spread of the average decreases as the number of repetitions increases, according to the rule, the expectation of the average remains the expectation of any single observation, as is intuitively obvious. Let us see how these ideas work, first for the binomial distribution (§9.2) where is the parameter and n the index, as when randomly removing n balls from an urn in which the proportion red is . It was seen in §9.3 that, for a single ball, the probability of being red, , and the expectation were the same. The expectation of the total number of red balls is therefore . Calculation shows that the spread of the number of red balls from n drawings is the square root of , in accordance with the square-root rule. (Readers who want to know where the comes from will find an explanation at the end of this section.) In particular, there is no spread when θ = 1 or θ = 0, with all balls of the same color, red or white respectively, for the two extreme cases. The Poisson distribution is even simpler, for if the expected number in a fixed period of say 1 hour is E, then over m hours the expected number is mE. Calculation shows that the spread for the 1 hour is √E, so that over m hours, is √(mE), again in accord with the square-root rule. In §9.10 the use of these results will be discussed. In the meantime here is an example of how variation can be handled with profit, but before presenting it, we promised to show the origin of above. The demonstration can be omitted without disturbing subsequent understanding.

Your probability of drawing a red ball from the urn is , and it was shown in §9.3 that if a quantity is defined as 1 if the ball is red, and 0 if white, your expectation of the quantity is also . More abstract language concerns a quantity, which is 1 if an event is true and 0 if false, when your probability and your expectation are the same. How far does the quantity depart, or spread, from its expectation? Clearly if the event is true and if false. Interest centers on the amount of the departure, not its sign, so we square the departures, getting with probability and with probability . The expected spread is, on multiplying the values by your probabilities and adding, . The first term is times ; the second is times , so that on addition the total multiple of is , leaving the final expectation as . Having used squares, the units will be wrong, so take the square root, obtaining as promised. Notice that the role of the square here has nothing to do with the square-root rule; it is introduced because we are interested in the magnitude of the departure from expectation, and not in its sign.

9.6 Variability as an Experimental Tool

Although in many ways variability, and the uncertainty it produces, is a nuisance, it can be exploited to provide valuable insights into matters of importance. Here is a very simple example of a procedure that is widely used in scientific experiments. An agricultural field station wishes to compare the yields of two varieties of wheat and, to this end, sows one variety in one half of a field and the second in the other half. As far as possible the two halves are treated identically, applying the same fertilizers and the same herbicides at the same times, ensuring that the two conditions of identical and independent repetitions are satisfied, except for the varietal difference. Suppose the yield is 132 tonnes for one variety and 154 for the other, then is the second variety better, or is the difference of 22 tonnes attributable to natural variation that is present in the growing of wheat? One way to investigate this is to divide each half of the field devoted to a single variety into two equal parts, each a quarter of the total, and to harvest the parts separately. Suppose the results are 64 and 68 for the first variety, totaling 132, and 74 and 80 for the second. The two differences, of 4 and 6, give an indication of the natural variation since the same varieties are being compared. The original difference of 22 between varieties is much greater than these, suggesting there is a real difference between the varieties, not attributable to natural variation. But stay, there is a slip there, this last difference of 22 is based on half fields, the others on quarter fields, so a correction is needed. Each yield based on half the field is the sum of two yields from the two quarters that make up the half, and therefore, by the square-root rule, has √2 times the spread of a yield based on a quarter. Therefore the varietal difference of 22, based on halves, has √2 times the spread associated with the natural differences, of 4 and 6, within the varieties. Dividing 22 by √2 gives about 15, a figure which is comparable with the 4 and 6. Being much larger than either of these, the suggestion is that there probably is a real difference between the two varieties because of the inflation from 4 and 6 to 15.

The discussion in the last paragraph is a very simple example of a technique called analysis of variance. (Variance is just a special measure of variation; it is the square of the standard deviation mentioned in §9.5.) Here the variation present in a body of data, the yields in the four quarters, is split up, or analyzed, into portions that can each be attributed to different facets, natural variation and variation between varieties, that may be compared with one another. A century ago it used to be common, when examining how different factors affected a quantity, to vary one factor at a time. Modern work has shown that this is inefficient and that it is better to vary all the factors simultaneously in a systematic pattern, and then split up the variability in such a way that the effects of the factors may be separated into meaningful parts. Another advantage of this method over that in which the factors are viewed separately is that the scientists can see how factors interact, one with another. For example, it is possible that neither factor on its own has any influence but both together can be beneficial. In §8.9 mention was made of a claim that eating a banana caused mucus. To test this one could vary the factor, banana, and measure the variation in mucus, yet, remembering Simpson in §8.2, it would be sensible to think of other factors that might be relevant, such as time of day, other foods consumed besides banana, and variation between individuals, and then devise an experiment that explored all factors and analyzed the variation. Determining the connections between bananas and mucus is not easy, and the same is true of many claims of an association that are made. As we have said before, a useful riposte to a claim is “how do you know?” Both Simpson's paradox and variation can make it hard to acquire sound knowledge.

9.7 Probability and Chance

It was seen in Chapter 7 that if there is a series that you judge exchangeable, the individual terms of which assume only two values, 1 or 0, true or false, success or failure, red or white, then you can regard the series as a Bernoulli series, with chance of red, about which you have a probability distribution. This result of de Finetti is now applied more generally. (Readers may like to refer to §7.8 in order to clarify their understanding of the distinction between the chance, and your probability, of an event). Take an uncertain quantity, which can assume any integer value, not just 1 or 0, and suppose you repeatedly observe it in a series that you consider exchangeable. An example is provided by a scientist who repeats the same experiment. Now concentrate on a particular value of the quantity, say 5, and observe whether, for each observation you get 5 or not; counting the former as a “success” and the latter as a “failure”. Imagine playing roulette and always betting on 5. You now have a series of successes and failures, which you judge exchangeable, because the complete observations of the quantity were. De Finetti's result may be applied to demonstrate that there is a chance such that your series of successes or failures is Bernoulli with that chance. Denote this chance by including the subscript 5 to remind us that success is obtaining 5. There is nothing special about 5, so that you have a whole slew of 's, one for each value of the quantity. Recalling from §7.8 that the chances correspond to limiting frequencies, they will all be positive and add to 1. In other words, they form a chance distribution.

It has therefore been established that if you have an exchangeable series, not simply of 0's and 1's, but of a quantity capable of assuming many integer values, then there is a chance distribution such that knowing it, you can regard the observations in the series as independent with your probabilities given by the chances. For example, your probability that the first observation is 2 and the second is 5 is by the product rule. This supposes that the chances are known. The analysis when the chances are uncertain for you is more complicated. Recall from §7.8 that chances are not expressions of belief but rather you have beliefs about them. So here you will have beliefs about and . To analyze your beliefs about the observations, it will be necessary to extend the conversation from the observations to include the chances, in generalization of the method used in §7.8 when the observations were only 0 or 1. The details are not pursued here.

The situation described in the last paragraph has found widespread use but, as presented there, it has a difficulty that there are lots of chances to think about, one for each value the quantity could possibly take. It is hard to contemplate so many and make uncertainty statements about them. It is often adequate to suppose all the chances are known functions of a few other values. We illustrate this with the Poisson distribution. Suppose that the operator experiences several tours of duty that are thought of as exchangeable. Then there will be a chance distribution of the numbers of calls per tour. But our operator in §9.4 made two additional assumptions, numbered (1) and (2), about independence and constancy within a tour. Adding these assumptions to that of exchangeability, the chances become severely constrained so that they are all functions of one value, the expectation E of the number of calls in any tour. It is unfortunate that the description, let alone the derivation, of these functions lies outside the modest mathematical level of this book. E is called the parameter of the Poisson distribution. Recall the tabulation in §9.4 for the Poisson distribution when E = 4. Generally with an exchangeable series, the usual practice is to suppose the chances are all functions of a small number of parameters. The Poisson has only one, E. The binomial has two, the index and what has been denoted by , though usually the index is known, so that is the sole parameter. In the example of §9.2 with n = 6, , the chance of 1 success, is and, if is known, is your probability of 1 success. Many chance distributions depend on two parameters, one corresponding to the expectation, the other to the spread. The Poisson is exceptional in that the spread √E is itself a function of the expectation E.

To recapitulate, a commonly used procedure is to have a series of observations that you judge exchangeable, such as repetitions of a scientific experiment, or a sample of households, with which, by de Finetti's result, you associate a chance distribution. By adding extra assumptions, as with the Poisson, or just for convenience or simplicity, you suppose these chances all depend on a small number, often two, of parameters. The parameters are uncertain for you and accordingly you have a probability distribution for them. Your complete probability specification consists of this parametric distribution and the chance distribution. With this convenient and popular model, you can update your opinion of the parameters as members of the series are observed. Thus with the Poisson parameter E, p (E) can be updated by Bayes rule, on experiencing r calls in a tour, to give

where is the Poisson chance. Thus for E = 4, r = 7, it has the value 0.060 from Table 9.1. Notice the difference between and p (r). The latter is your probability for r calls when E is uncertain, and is calculated by extending the conversation from r to include E, as in §7.5. p (r) would be relevant when you were starting a tour with uncertain expectation and wished to express your uncertainty about the number of calls you might experience in the tour.

9.8 Pictorial Representation

There are quantities that do not take only integer values. We met one in §9.5 when considering the uncertainty about the time to the next phone call. At 3.45 this time can take any value, not just an integer. In practice we measure it to the precision of a convenient unit, like a minute, but in some situations more precision may be needed and recording to the nearest second might be used. Such a quantity is said to be continuous, whereas the integer-valued ones are discrete. To see how the associated uncertainties can be handled, it is convenient to use a pictorial representation. Figure 9.1 describes the Poisson distribution with expectation 4 in Table 9.1. The horizontal axis refers to the number of calls and upon this rectangles are erected, each with base length of 1 and each centered on a possible number of calls, 0, 1, 2, and so on. The height of the rectangle is the probability, according to the Poisson with expectation 4, of the number of calls included in the base. Thus that centered on r = 2 has height 0.15. The vertical axis thus refers to probability. The important feature of this manner of representing any distribution of an integer-valued, uncertain quantity is that the area of the rectangles provides probabilities, since the base of the rectangle is 1. The key element in the interpretation of such figures is area.

Figure 9.1 Poisson distribution with E = 4 from Table 9.1.

This style of representation is now extended to continuous, uncertain quantities, beginning with the time to wait for a call as experienced by the operator. Table 9.2 provides your probabilities for the 12, 10 minute intervals within the 2 hours of the tour. Thus your probability that you will have to wait between 40 and 50 minutes for the first call is 0.074. In addition, your probability of having to wait more than 120 minutes is 0.018. This event corresponds to having no calls in the tour, agreeing with the corresponding entry in Table 9.1. Since the tour ends at 2 hours, this value will be omitted from future calculations. Figure 9.2 gives a pictorial representation along the lines of Figure 9.1. Thus on the first interval from 0 to 10 minutes is erected a rectangle of height 0.0284, so that its area, in terms of minutes, is 0.284, your probability of waiting between 0 and 10 minutes for the first call. Remember that the important feature here is the area of the rectangle, not its height. (The reason why the vertical axis is labeled “density” is explained later.) Notice confirmation of the surprising fact pointed out in §9.4 that the areas, and therefore the probabilities, diminish as time increases. Thus there is a chance of more than a quarter that the wait will be less than 10 minutes, despite the fact that only 4 calls are expected in 120 minutes.

Table 9.2 Probabilities of the time to wait for the first call, divided into 10 minute intervals with the upper limit of each interval given E = 4 for a tour of 120 minutes.

Figure 9.2 Pictorial representation of Table 9.2.

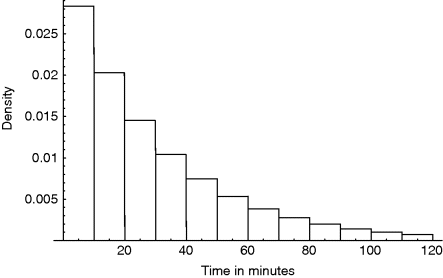
Figure 9.3 repeats Figure 9.2 with, superimposed upon it, the same rectangular representation when intervals of 5, rather than 10, minutes are used. Thus between 0 and 5 the rectangle has height 0.0307 and therefore area 0.154, your probability of getting a call almost before you have time to settle in. Between 5 and 10, the height is 0.0260, while the area and probability is 0.130. The two probabilities add to give 0.284, agreeing with Figure 9.2. Thus the two thinner rectangles, base 5, have total area to match that of the thicker rectangle, base 10, and the three heights are all about the same, around 0.03. Similar remarks apply to the other pairs. Now imagine these procedures for 5 minute and 10 minute intervals repeated for intervals of 1 minute, then 1 second, continually getting smaller. The rectangles will get thinner but their heights will remain about the same, so that if we concentrate on the tops of them they will eventually be indistinguishable from a smooth curve. This curve is also shown in Figure 9.3. It starts at height 0.033, or exactly 4120, corresponding to an expectation of 4 in 120 minutes, and descends steadily. Although it has only been shown up to the end of the tour, it continues beyond, as would be needed if the tour were longer.

Figure 9.3 Pictorial representation of Table 9.2 with further division into 5 minute intervals and also the continuous density.

It is this curve that is important. Its basic property is that the area under the curve between any two values, say between 40 and 50 minutes, is your probability of the quantity lying between those values, of waiting more than 40 but less than 50 minutes. It is sometimes described as a curve of probability but it is not probability, it is the area under it that yields our uncertainty measure. Here it will be referred to as a probability density curve, or since this is a book about probability, simply as a density. (The familiar density is mass per unit volume; ours is probability per unit of base.) It is often referred to as a frequency curve because if you were to observe the quantity on a series of occasions that you judged exchangeable, the areas would agree with the frequencies with which the quantity lay between the boundaries of the areas.

9.9 Probability Densities

There are three matters that need attention before we leave densities. The first is to remark that the ideas of this section easily extend to two uncertain quantities in a manner similar to the extension to two events in Chapter 4. Denote the two quantities by X and Y and divide both their ranges into intervals of equal, small lengths as in Figure 9.2. Next consider the event that both X lies in a selected interval and Y in another. Then we can think of X and Y lying in a square, bordered by the two intervals, and can erect a “tower” on that square of a height such that the volume of that tower is your probability that both X and Y lie within the square base of that tower. This is the same procedure used to construct Figure 9.2 with length of an interval replaced by area of a square, and area of the rectangle erected on the interval by volume of the tower erected on the square base. In this manner the height of the tower is the density p (x, y) where (x, y) is any point in the base area. The pictorial representation is not normally useful because volumes are hard to picture, but the concept of density is most important. The procedure adopted here extends to three, or more, quantities.

The second point is that the results developed in this book for probabilities extend to densities. The point will now be demonstrated for Bayes rule but it applies generally. Consider Figure 9.3 and denote by w the width of the interval into which the range of the uncertain quantity, X, the waiting time, has been divided. The figure shows the cases w = 10, solid lines, and w = 5, dotted. If p (x) is the density at value x of X, then p (x)w is your probability that X lies in the interval that contains x. In other words, p (x)w is a probability and obeys all the rules of probability. Recall Bayes rule (§6.3), omitting reference to the knowledge base,

and let E be the event that X lies in the interval of width w that contains x. Then and where and are densities. Notice there are two densities for X here, one given F, the other on the knowledge base, and the range has been divided into intervals of the same width w. Inserting these values into the formula, the w s cancel and

exactly the same but with densities in place of probabilities. If F similarly corresponds to a continuous quantity Y, the interval there will occur on both sides of the equation and therefore again cancel. Hence Bayes rule reads

The third matter is a variant of the addition rule that says that if F_i form a partition, then p (E) is equal to the sum of the terms p (EF_i ) over all values of i (§9.1). For a density p (x, y) of two uncertain quantities, X and Y, we may sum over all values of y (the technical term is integrate) to obtain the density of X alone, p (x). This is often called the marginal density. The concept is frequently used in statistics, Chapter 14.

9.10 The Normal Distribution

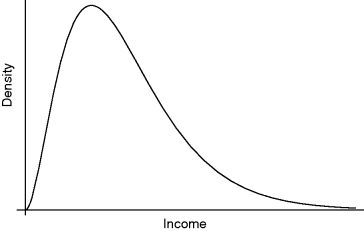
This representation through a density is most useful, both to the mathematician and to lay persons, for describing their uncertainties. Figure 9.4 presents a typical density for incomes in a population. We have deliberately refrained from giving the units since these will differ from country to country. Recall the essential aspect is the area under the curve between any two values, so that keeping the distance between these values constant, it is the height of the density that matters. Starting from the left, the density begins with low values, showing that few people have very small incomes. It rapidly ascends to a point where there are many people with these incomes. The further descent from the maximum is much slower than the ascent, showing that incomes somewhat above the common value do occur fairly frequently. The curve continues for a very long way, showing that a few people receive very high incomes. This type of income density is common in market economies and large spread thought undesirable.

Figure 9.4 Density of income distribution.

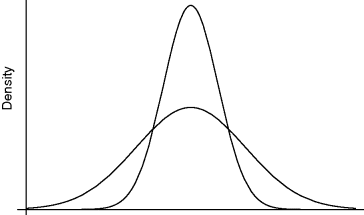
There is one type of density that is very important, both because it has many simple, useful properties that make manipulation with it rather easy, and because it does arise, at least approximately, in practice. Two examples are shown in Figure 9.5. Features common to both are symmetry about the maximum, in a shape reminiscent of a bell, and continuing at very small values for a long way. The maximum occurs at the mean, or expectation, so that the two in Figure 9.5 have the same mean. They differ in their spread. As the density flattens out, the value at the maximum necessarily decreases to keep the total area at one. These are examples of a normal density, the name being somewhat unfortunate because a density that is not normal, like that for income, is not abnormal. An alternative name is Gaussian. Each normal density is completely described by two parameters, its expectation or mean and its spread. The latter can be described nonmathematically in terms of the following property expressed in terms of a measure of spread called the standard deviation, abbreviated to s.d. (This was the measure used with the binomial, and the Poisson √E, and also mentioned in §9.5.)

Figure 9.5 Normal densities with identical means, different spreads.

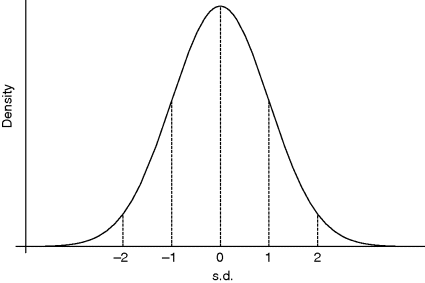
For any normal density the probability of being within 1 s.d. of the mean is about 23, within 2 s.d. 1920 and within 3 s.d. 9971000.

Thus two-thirds of the total area under the curve is contained within 1 s.d. Values outside 2 s.d. only occur with frequency 120, or 5%. This latter figure has been unduly popular with statisticians. Values outside 3 s.d. are extremely rare, rather less than 3 in a thousand occur there. Figure 9.6 illustrates this property. One important property of the normal is that if X is a quantity with a normal distribution, then rescaling it by multiplying by a constant a and relocating it by adding a constant b, results in another normal quantity whose expectation is similarly rescaled and relocated and whose s.d. is multiplied by a, the relocation having no effect on the spread.

Figure 9.6 Normal density with zero mean and unit s.d.

Here are some reasons for the popularity of the normal distribution. The binomial (§9.2) with index n and parameter is, for large n, approximately normal, the approximation being best around θ = and worst near 0 and 1. Similarly the Poisson is approximately normal for large expectation E. This latter result can be illustrated with the Poisson in Table 9.1 with mean, or expectation, 4. The s.d. is √E = 2, so the values 2, 3, 4, 5, and 6 are within 2 s.d.'s of the mean. The total probability of these is

rather larger than the value 23, about 0.67, quoted above. But recall we are approximating a discrete quantity, number of calls with the Poisson, by a continuous one, the normal. Looking at Figure 9.1, it will be seen that the rectangle at r = 2 for the Poisson has only half its area within 1 s.d. of 4. Therefore the probability at r = 2 of 0.15 should be halved, as should the probability of 0.10 at r = 6. This reduces the total probability of 0.81 above by 0.07 + 0.05 = 0.12, yielding 0.69 in excellent agreement with the normal value of 0.67. The halving here may appear suspect but it is genuinely sound.

Suppose you take (almost) any quantity, make a number n of observations of it that you judge exchangeable and then form their average, their total divided by n; then this average will have, to a good approximation, a normal distribution. Your expectation of the normal will be the same as that of the original quantity, the s.d. will be that of the original quantity divided by √n in accordance with the square-root rule in §9.5. Since so many quantities are, in effect, averages, the normal distribution occurs reasonably often, though there is a tendency to use it even where inappropriate because of its attractive properties. Doubtless this tendency will diminish now that our computing power has increased. The result stated in the first sentence can be applied to both the binomial and Poisson distributions to justify the assertions in the previous paragraph about their approximations by the normal. Thus the binomial is based on a quantity taking values 0 and 1 whose values are totaled to give the binomial. The average is just this total divided by n, so the normal distribution for the average will translate, by the result above, into a normal distribution for the total. The s.d. of the 0–1 quantity, we saw in §9.5, was . That for the average will be by the square-root rule, and that for the total .

A classic example of a normal distribution is provided by the heights of men in a population. The same remark applies to women but since, in respect of height, men and women are not exchangeable, the expectations are different, women being slightly shorter. The s.d.'s are about the same. A similar normal property holds for most measurements of lengths on people, like those of leg lengths. This fact is of use to clothing manufacturers since they know, for example, that only about 1 in 20 of the population will lie outside 2 s.d.'s of the mean.

9.11 Variation as a Natural Phenomenon

In §1.3, it was mentioned that people do not like uncertainty and often invent concepts that appear to explain it. One instance of this is the introduction of gods who control variable phenomena like the weather, but we do not need to be as drastic as this, for people are prepared to see real cause and effect where nothing but natural variation is present. Here is an example that occurred recently and provoked action to remove discrepancies, which was unnecessary because only natural variation was present and the discrepancies explained in terms of it. The original figures have not been used because to do so would involve subtleties that might hide the key point to be put across. Effectively the figures have been rounded to present equalities that were not there originally but the conclusions are unaffected. Before entering into the discussion recall several facts learnt earlier in this chapter. First, the Poisson distribution is present when there are a lot of independent occasions when something might happen but the chance of the happening is small. In our example, there are a lot of people but each has a small chance of dying from the disease being considered. Second, the spread about the Poisson mean, expressed through the s.d., is equal to the square root of that mean. Finally, for expectations that are not too small, the Poisson distribution is well-approximated by the normal, for which about 2 out of 3 of the observations lie within 1 s.d., and 19 out of 20, within 2 s.d. of the mean, or expectation. With all these facts at our disposal, facts it might be pointed out that were likely unknown to the participants in the study, we can proceed with the example.

A disease had a death rate per year throughout a region of 125 per 100,000 people older than 30 years. The region was divided into 42 health authorities, each responsible for 100,000 such persons, and each recorded the number of deaths in a year from the disease among people older than 30 years in their area. There were therefore 42 instances of variation about an expectation of 125 and it is reasonable to approximate the situation with 42 examples of a Poisson with mean 125. Applying the square-root rule, the square root of 125 is about 11, so that it would be anticipated that about two-thirds of the authorities would have rates between 114 and 136, while only 1 in 20, just 2, would have rates outside an interval of twice this width, from 103 to 147. In fact there were three, at 97, 148, and 150. This is in good agreement with the Poisson proposal. Seeing these figures, the administrators in the health service were worried that two authorities had death rates 50% greater than that of the best authority. The media looks with horror at this, scents a story, and both groups try to find reasons for the discrepancy. The administrators punished the apparent errant authorities and praised the successful. In fact they were inventing causes for a variation that is natural to the patterns of death. Randomness is enough explanation and it is doubtful if anything can be done about that. Basically, the square-root rule was not appreciated.

Indeed, we can go further and say that if all, rather than two-thirds, of the authorities had death rates within 1 s.d., that is between 114 and 136 as natural variation suggests, there would have been grounds for suspecting that some falsification of the figures had occurred in order to comply with standards laid down from on high. I once met such a case, involving several producers that had agreed to provide their data prior to the possible introduction of some legislation, The figures were in too good agreement. Enquiry revealed that the producers had got together and some had altered their results so that none appeared out of line.

There is more that can be said about the effect of natural variation. Consider that “bad” health authority with 150 deaths and suppose natural variation is allowed to operate. The result will be that next year the Poisson will again obtain and your probability that, with your expectation still at 125, of getting less than 150 deaths in that authority is almost 1. In other words, the authority will improve without any intervention. This gives bureaucrats a fine opportunity to castigate the apparently errant authority, to enforce changes and then sit back and think how clever they have been in reducing the rate, when nothing has been accomplished except bullying of staff. A failure to recognize natural variation may occur in many fields; education has obvious parallels to health provision. A less obvious parallel is the Stock Exchange, where some people are thought to be better at predicting the market than others. Are they; or is it natural variation? Does management recognize talent or does it just pick the best in the Poisson race?

My concern here is to emphasize that some variation is inherent in almost any system and that its presence should not be forgotten. That is not to say that all variation is natural, for one of the tasks of a statistician is to sort out the total variation into component parts, each having its proper attribution. A simple example of this was presented in §9.6. In that agricultural example there was no inherent measure of spread, as there was in the health example with the square-root rule, and the natural variation had to be separately evaluated. No doubt there are cases of death-rate variation that are causal and exceed natural variation; my plea is for uncertainty to be appreciated as a naturally arising phenomenon that can be handled by the rules of probability. It appears to be a long way from the balls in urns to the Poisson and the square-root rule but the connection is only coherence exhibiting its strength. We often say “you are lucky” but how often are we wrong and fail to recognize the skill involved?

9.12 Ellsberg's Paradox

It has been emphasized in §2.5 that there is a distinction between the normative, or prescriptive, approach to uncertainty adopted in this book and the descriptive approach concerned with describing how people currently think about uncertainty. The concentration on normative ideas does not imply that descriptive analysis is without value; on the contrary, the study of people making decisions in the face of uncertainty may be very revealing in correcting any errors and persuading them of the normative view. And, recalling Cromwell (§6.8), it is possible that good decision makers may be able to demonstrate flaws in the normative theory and, like the Church of Scotland, I may be mistaken. The contrast between normative and descriptive approaches is clearly brought out in paradoxes of the Ellsberg type, discussed in this section. The results are not used in what follows and may be omitted by those who do not like paradoxes. Its presentation has been delayed until now because understanding depends on the concept of expectation developed in §9.3.

Consider our familiar urn, this one containing 9 balls. (9 is used because we want to divide by 3, which 10, or 100, do not do exactly.) 3 of the balls are red, the other 6 are either black or white, with the number b that are black uncertain for you. One ball is to be drawn from the urn in a manner that you think is random and you are asked to choose between the two options displayed in Table 9.3.

Table 9.3 First pair of Ellsberg options.

Here U is a positive number representing a prize and 0 means no prize. Thus option X gets you the prize if the withdrawn ball is red, whereas Y rewards you if it is black; there is no prize with either option if the ball is white. You are also asked to choose between two options in Table 9.4 using the same urn under the same conditions.

Table 9.4 Second pair of Ellsberg options.

Thus option V rewards you provided the ball is red or white, whereas W rewards if black or white. Note that you are not being asked to compare an option in one table with any in the other. Everyone agrees V is better than X and W than Y because white balls pay out in the former but not in the latter. No, you are asked to choose between X and Y, and between V and W. What would you do?

Consider first the normative approach where the only thing that matters is your probability p (U) that you will get the prize. Since you are uncertain about the number of black balls, you will have a distribution p (b) over the 7 possible values from 0 to 6, and p (U) will depend on this. For option X, p (U) is 39 because of your belief in the random withdrawal and the fact that the value of b is irrelevant. For option Y the calculation must be more elaborate. If you knew the number b of black balls, , so if you extend the conversation to include b, p (U) will be the sum of terms bp (b)9 over the 7 possible values of b. The result will be E 9 where E is your expectation for the number of black balls in the urn. (You may care to refresh your memory by looking at the same argument in §9.3.) Consequently you compare p (U) = 39 for X with E 9 for Y, and Y is preferred to X if ; if you prefer X and with E = 3 you are indifferent between X and Y. Exactly the same type of argument shows that W is preferred to V if ; if you prefer V and with E = 3 you are indifferent. Consequently your choices depend solely on the number of black balls you expect to be in the urn and you either choose both X and V, both Y and W, or express indifference in both cases.

We now pass to the descriptive approach. Several psychologists have performed experiments with subjects, most of whom have no knowledge of the probability calculus, and asked them to make the choices between the same options, with the result that most prefer X to Y and also W to V. This disagrees with the normative approach where a preference for X, because the expectation of b is less than 3, must mean a preference for V above W. The two approaches are therefore in direct conflict. When the subjects are asked why they made their choices, the usual reply is that they preferred X to Y because with X they knew the numbers of balls in the urn that would cause them to win, namely 3, whereas with Y they did not. The additional uncertainty with Y, over that with X, was thought to be enough to make X the choice. Similarly W had 6 balls that would yield the prize, whereas with V the number, 9 − b, is unknown, so W is preferred. We have a clear example of the dislike of uncertainty (§1.3), here sufficient to affect choices.

Which is more sensible—the normative or descriptive attitudes? Before we answer this, let us consider the nature of the disagreement and notice that it concerns coherence. Suppose you, in the technical sense, have seen a subject prefer X above Y; then you would see nothing unsound in the choice, merely noting that the subject must have an expectation for b of less than 3. Similarly if another subject has preferred W to V, then you think it sensible with their expectation being more than 3, so that both subjects are above criticism. But suppose you see the same subject make both preferences, then you think they are foolish, or incoherent, the first preference not cohering with the second. Here is a clear example of a phenomenon that I think is very common: the individual judgments, considered in isolation, are often sound, the flaw is that the judgments do not fit together, they are inconsistent, or, as we say, incoherent.

How does this incoherence arise? Both you and the subjects recognize that the key element is the unknown number, b, of black balls. The subjects worry about it and try to avoid it as much as they can by choosing X and W. You, by contrast, face up to the challenge, recognize that b is uncertain, and use a probability distribution for it. (You go further and note that the whole distribution does not matter, only the expectation is relevant, a point we return to below.) Now you have a problem; what is your distribution? I put it to you that the development in §3.4 is compelling and that you must have a distribution; the trouble is that you do not know how to assess it. Consider an analogous situation in which you do not have to make a choice between options but between two objects, the prize being awarded if you select the heavier one. There is no doubt in your mind that associated with each object there is a number called its mass but you do not know it. If you could see the objects, you could guess their masses, though the guesses would not be reliable. Were you able to handle them, better guesses could be made, and if you had an accurate pair of scales, you could do much better. Mass here is like probability in the options; you know it exists but have trouble measuring it. In other words, the normative person, you, knows how to proceed coherently with the options but has a measurement problem. In contrast, the subjects did not know how to proceed and therefore shied away from options that involved uncertainty, thereby becoming incoherent.

In the problem as presented here, it is somewhat artificial and all of us would have difficulty with the measurement of p (b). A common attitude is to say that you can see no reason as to why any one of the 7 possible values is more probable than any other, so use the classical form of §7.1 with p (b) = 17 for all 7 values of b. The expectation is then 3 and you would be indifferent between X and Y, and between V and W. Most published analyses of the problem assume, sometimes implicitly, that the classical form obtains. On the contrary, you might receive information that the number of black balls had been selected by throwing a fair die and equating b with the number showing on the die. In that case the expectation is 3 (§9.3) leading to your choice of Y rather than X, and W rather than V. In another scenario you might have witnessed several random drawings from the urn and noticed the colors of the exposed balls. You would then have updated your knowledge by Bayes rule and have a distribution based on the data. An extreme possibility is that you are told the values of b, when X and V are selected if you are told b = 0, 1, or 2; Y and W if b = 4, 5, or 6; and you are indifferent if b = 3.

For anyone who is still unconvinced that the normative approach is sensible and the subjects unsound in the Ellsberg scenario, consider the following two arguments. First, suppose you were informed of the value of b, as at the end of the last paragraph, then whatever value it was you would never choose both X and W as the subjects did; so why choose them when uncertain about b ? (We return to this point when the sure-thing principle is discussed in §10.5.) Second, in the choice between X and Y, the white balls do not matter since in neither option do they yield a prize, so that the final column of the table may be omitted. Similarly in the choice between V and W, the white balls are irrelevant, always producing the prize and again the final column may be deleted. When the final columns are removed from both tables, the remaining tables are identical. So if you choose the first row in one, you must do the same in the other, and the subjects' selection is ridiculous.

One final point before we leave Ellsberg. The paradox shows us that the only aspect of the uncertainty that matters is your expected number of black balls, and that your actions should be based solely on this number. This lesson is important because we shall see when we come to decision analysis in § 10.4 that again it is only an expectation, rather than a distribution, that is relevant. People often have difficulty with the idea of making an important decision on the basis of a single number, so let Ellsberg prepare you for this feature. Mind you, the expectation has to be carefully calculated, as we shall see.