Chapter 14
Statistics
14.1 Bayesian Statistics
There has been an extensive development of the ideas presented in this book within the field of statistics. Statistics (in the singular) is the art and science of studying statistics (in the plural), namely data, typically in numeric form, on a variety of topics. An early historical example was the collection of data on the production of wheat every year. Nowadays statistics covers any topic in which data are available, in particular within the scientific method. Once the data are available, statisticians have the task of presenting and analyzing them and, as a result, the activity of statistics (in the singular) has been developed. Within science, most of the effort has been devoted to models where, as we have seen, data, now denoted by x, are modeled in terms of a parameter 
, through a probability distribution of x for each value of 
, 
. A simple example is the measurement x of the strength 
of a drug, where there will be uncertainty because all people do not react in the same way to the drug. If x contains measurements on several people, the object of the investigation is to assess the strength 
; we say we want to make an inference about 
. A typical inference might be to say that 
is 0.56 ± 0.04 in suitable units.
In the probability system developed in this book, the problem of inference about a parameter is easily solved, at least in principle, by introducing a prior distribution 
for the parameter. This expresses your uncertainty about 
based solely on background knowledge that will remain fixed throughout the inference and therefore omitted from the notation. With the acquisition of data x, the posterior distribution 
may be calculated using Bayes rule (§6.3):
In view of the central role played by the rule, this treatment of data is termed Bayesian statistics. The distinguishing feature is that the model is extended by the introduction of the prior, the justification being the general one that uncertainty, here of 
, is described by probability. Recall (§9.1) that the denominator in (14.1) is found by extending the conversation from x to include 
, which means adding the numerator of the rule over all values of 
under consideration. It is important to recognize that the posterior distribution 
provides all the information you have about the parameter, given the data and background knowledge. The inference is complete and there is nothing more to be said. However, a distribution is a complicated concept and you may wish to extract features from it, if only for ease of comprehension. An obvious example is your expectation of 
, that is, the mean of the distribution of the parameter. Another popular choice is the spread of the distribution (§9.5), which is valuable in telling you how precise is your information. It is usual to refer to the expectation as an estimate of the parameter. There are other possible estimates; for example, with income distributions, which typically have some very high values, the median of the distribution, where your probability of exceeding it is ½, may be preferred. Any feature of the distribution that helps you appreciate your uncertainty about the parameter can be employed. These are questions of comprehension, not logic.
One feature of Bayesian statistics is worth noting because many popular statistical procedures do not possess it. It is clear from the rule that once you have the data x, the only aspect of it that you need to make the complete inference is the function 
, for the fixed x seen, and all values of 
. If you doubt the truth of this statement because of the appearance of 
in the denominator of the rule, recall that 
is calculated by extending the conversation from x to include 
, so still only including the terms 
for the observed data. This result is commonly stated as the following:
Notice that this refers solely to the data's contribution to the inference; the other ingredient in Bayes rule is your prior for the parameter. What the likelihood principle requires you to do is to compare your probability of the data for one value of the parameter with its value for another, in essence, the likelihood ratio (§6.7). This is another example of the mantra that there are no absolutes, only comparisons. The principle was encountered in the two-daughter problem (§§12.4 and 12.5) where the omission of the likelihood in the formulation of the problem made it ambiguous.
In many scientific cases it is desirable to include more than one parameter in the model. In an example in the next section, it is necessary to include the spread of the data distribution, as well as the mean. With two parameters, φ and ψ (psi), the whole of the previous argument goes through with
where 
) is your prior distribution for the two parameters. Again, in principle, this causes no difficulty because 
is obtained by summing 
over all values of ψ, essentially the marginal distribution of φ (§9.8). If φ is the parameter of interest, ψ is often called a nuisance parameter, and the nuisance can be eliminated by this summation. Extra nuisance parameters are often included because they make the specification of the model simpler, often by introducing exchangeability, a concept that is almost essential for an alternative approach to statistics studied in the next section. Sometimes it is useful to introduce many nuisance parameters and then have a distribution for them. The death-rate example of §9.10 provides an illustration, with ψ i connected with region i. Then it is useful to have a probability distribution for these nuisance parameters. Models of this type are often termed hierarchical.
In principle, the Bayesian method is simple and straightforward. In practice there are mathematical difficulties mainly in the summation, over φ when calculating 
, and over ψ when eliminating a nuisance parameter. The development of Bayesian ideas was hindered by the lack of easy methods of summation, or what mathematicians term integration. However, with the arrival of modern computers, it has been found possible to do the integration and perform the necessary calculations to obtain your posterior distribution, and hence the complete inference. Aside from the mathematical difficulties, the usual objection to the Bayesian approach has been the construction of the probability distributions, especially the prior. Exchangeability is often available for the model distribution. It is the use of background knowledge to provide a prior that has led to most criticism. The rewards for having a prior are so great that the advantage usually outweighs the difficulty. Notice that the Bayesian method has two stages. In the first, you have to think about your probabilities. In the second, thinking is replaced by calculations that the computer can perform. In the next section, we present an example of a simple, but common use of the method. In the section on significance tests (§14.4), a further example of the use of Bayesian methods is provided.
14.2 A Bayesian Example
In this section, a simple example of the Bayesian approach to statistics is examined that is often appropriate when you have a substantial amount of data, perhaps 100 observations. It is based on extensive use of the normal distribution (§9.9) and before reading further, the reader may wish to refresh their understanding of this distribution, so beloved by statisticians for its attractive properties, making it relatively easy to manipulate. Recall that it has two defining features, its mean and its spread. The maximum of the density occurs at the mean, about which the density is symmetric. The spread describes how far values can depart from the mean. The mean is alternatively termed the expectation of the uncertain quantity having that distribution. The spread is the standard deviation (s.d.). Figures 9.5 and 9.6 illustrate these features. The notation in common use is to say that an uncertain quantity has a normal distribution of mean φ and s.d. s, writing 
.
In the basic form of the example, the data consist of a single real number x, resulting from just one observation, which has a 
distribution. Here φ is the parameter of interest and s is supposed to be known. The model might be appropriate if the scientist was measuring φ, obtaining the value x, using an apparatus with which she was familiar, so knew s from previous experiences with measuring other quantities using the apparatus. The method is often used where x has been extracted from many observations, since, due to a result in the calculus, such a quantity is often normally distributed. That describes the term 
in Bayes rule. There is no need to refer to s in that rule because it is known and can therefore be regarded as part of your background knowledge. It remains to specify the prior, 
, which is also supposed to be normal, the mean denoted by μ (Greek `mu'), and the spread by t, 
. In practice, μ will be your most reasonable value of φ, your expectation, and t will describe how close to μ you expect φ to be. If you know little about φ, t will be large, but if the data are being collected to check on a suspected value of φ, t will be small. With 
and 
both defined, all is ready to apply Bayes rule.
Theorem If x is 
given φ and φ is 
, then the posterior distribution of φ, given x, is also normal with
The most remarkable and convenient feature of the theorem is that normality of the data, and of the prior, results in the posterior of the parameter also being normal. This is part of the reason why normality is such an attractive property, for it is preserved under Bayes rule. That normality also frequently arises in practice makes the theorem useful as well as attractive. Unfortunately, it is not possible to prove that the theorem is correct with the limited mathematics used in this book (§2.9) because to do so would require an understanding of the exponential function. Throughout this book, I have tried to show you how the results, such as Bayes and the addition and multiplication rules, follow from some comparisons with the standard of balls from an urn. There you do not need to trust me, you can see it for yourself. Here I regretfully have to ask you to trust me.
The expression for the posterior mean (14.2) is best appreciated by comparison with Equation (7.2) where a posterior probability was a weighted average of data f, and prior assessment g, the weights being the number of observations n in the data and your prior confidence m in g. Here we again have a weighted sum; x is weighted by 
, the prior μ by 
. If the observation x is precise, 
is small and a lot of attention is paid to it. Similarly, if you are originally confident about μ, 
is small and it receives attention. In most practical cases, 
is smaller than 
, so that most weight goes on x. Notice that it is the reciprocals of the squares of the spreads, 
and 
, that provide the weights. There is no generally accepted term for them and we will refer to them as weights. With that definition, the formula (14.3) is readily seen to say that the posterior weight, the reciprocal of the square of the spread, is the sum of that for the data, 
, and that for the prior 
.
Suppose that a scientist was measuring an uncertain quantity and expressed her uncertainty about it as normal with expectation 8.5 but with a spread of 2.0. Recall from §9.9 that this means that she has about 95% probability that the quantity lies between 12.5 = 8.5 + 4 and 4.5 = 8.5 − 4, the values 4 being twice the s.d. or spread. Using the apparatus, assumed normal of spread 1.0, suppose she obtains the observation x = 7.4. Then the theorem says that she can now assess the quantity to have expectation:
The denominator here shows that the spread is 
. The expectation is a little larger than the direct measurement, which was lower than she had expected, but the increase is small since the apparatus spread was only half the spread of the prior view. As the prior view gets less reliable, the weight 
decreases, and the role of her prior opinion decreases, with the raw value of 7.4 ultimately accepted. Many statisticians do this as routine. According to Bayesian ideas, this is regrettable but here it is not a bad approximation unless you have strong prior knowledge. A possibility that can arise is that the observation x is well outside the prior limits for φ, here 4.5 and 12.5, even allowing for the spread s of x. If this happens, it may be desirable to rethink the whole scenario. Coherence cannot be achieved all the time. It is human to err; it is equally human to be incoherent.
It is common to take several measurements of an uncertain quantity, especially in medicine where biological variation is present. The above method easily extends to this case with interesting results. Suppose that n measurements are made, all of which are 
and are independent, given φ. Then the likelihood function is dependent on the data only through their mean, the total divided by their number. In the language of §6.9, the mean, written 
, is sufficient. It is often called the sample mean to distinguish it from the true mean φ. (Another convenient property of normality.) We saw with the square-root rule in §9.5 that the mean has a smaller spread than any single observation, dividing the spread s by 
. It can then be proved that the theorem holds for n such observations with x above replaced by 
and 
by 
. Let us try it for the above numerical example with 10 measurements giving a mean of 7.4, the same as for a single measurement originally, so that increasing the number can be more easily appreciated. The posterior mean will be
and the spread 
. The effect of increasing the number of measurements has been to bring the expectation down from 7.62 to 7.43, nearer to the observed mean of 7.4, because of the added weight attached to the mean, compared with that of a single measurement. Also, the posterior spread has gone down from 0.89 to 0.31. Generally, as n increases, the weight attached to the mean increases, whereas that attached to the prior value stays constant, so that ultimately the prior hardly matters and the posterior expectation is the mean 
with spread 
according to the square-root rule. This provides another example of the decreasing relevance of prior opinion when there is lot of data.
An unsatisfactory feature of this analysis with normal distributions is that the spread of the observations, s, is supposed known, since there is information about it through the spread observed in the data. The difficulty is easily surmounted within the Bayesian framework at some cost in the complexity of the math, which latter will be omitted here. It is overcome by thinking of the model, x as 
, being described, not in terms of one parameter φ, but two, φ and s. As a result of this, your prior has to be for both with a joint distribution 
. It is usually thought appropriate to suppose that φ and s are independent on background knowledge, so that the joint distribution may be written as 
. With 
as before, it only remains to specify 
. Having done this, Bayes rule may be applied to provide the joint posterior distribution of φ and s, given the data. From this, it is only necessary to sum over the values of s to obtain the marginal distribution of φ, given the data. The details are omitted but a valuable result is that, for most practical cases, the result is essentially the same as that with known s, except for really small amounts of data. The previously known spread needs to be replaced by the spread of the data. As a result, save for small amounts of data, the posterior distribution of φ remains normal. When the normal approximation is unsatisfactory, the exact result is available. The treatment of this problem with s uncertain, though from a different viewpoint from that used here, was made a little over a century ago and was an early entry into modern statistical thinking. The exact distribution is named after its originator who wrote under the pseudonym “Student”, and is well tabulated for all values of n.
Another example of the Bayesian method is given in §14.4 with a discussion of significance tests.
14.3 Frequency Statistics
It is unfortunately true that many statisticians, especially the older ones, reject the Bayesian approach. They have two main, related reasons for the rejection: first that your prior 
is unknown, second that it is your posterior, your inference, so that the procedure is subjective, with you as the subject whereas science is objective. These two objections are discussed in turn. It is certainly true that, prior to the data, φ is unknown, or as we would prefer to say, uncertain, but it would be exceptional not to know anything about it. In the relativity experiment (§11.8), the amount of bending could not be large, for if so, it would have been noticed, and the idea of it being negative, bending away from the sun, would be extraordinary. So that there was some information about the bending before the experiment. Indeed, what right has any scientist to perform an experiment to collect data, without understanding something of what is going on? Has the huge expenditure on the Hadron collider been made without some knowledge of the Higgs boson? In practice, scientists often use the information they have, including that about φ, to design the experiment to determine x; indeed it would be wrong not to use it, but then abandon that information when they make an inference about φ based on x. To my mind, this practice is an example of incoherence, two views in direct conflict. Some statisticians have tried to find a distribution of φ that logically expresses ignorance of φ but all attempts present difficulties.
The idea that nothing is known about the parameters before the data are observed, may be unsound, but those who support the idea do have a point: so often it is hard to determine your distribution for the parameters. We have seen examples of this difficulty, even in simple cases, in Chapter 13. Methods for the assessment of a single parameter are deficient; the assessment of several probabilities is more sensible, so that the full force of coherence may be exploited. The parameter φ in the model is part of the theory, so that there are opportunities to relate φ to other quantities in the theory. My view is that it would be more sensible to devote research into methods of assessment, rather than use, as many do, the incoherent techniques we investigate below. Another curious feature of this reluctance to assess a prior is the casual, almost careless, way in which the probability distribution of the data is selected; normality is often selected because of its simple properties. Sometimes there is a practical reason for choosing the data distribution using frequency considerations (§7.2). Many experiments incorporate some form of repetition, leading to exchangeability, and the concept of chance (§9.7). For example, with personal incomes, the subjects may be thought exchangeable with respect to income and their values plotted to reveal a distribution with a long tail to the right, corresponding to the few rich people.
The second objection to Bayesian ideas is that they are subjective. All the probabilities are your probabilities, whereas a great advantage of science is that it is objective. One counter to this is provided by the result that if two people have different views, expressed through different priors, then the use of Bayes rule, and the likelihood that they share, will ultimately lead them to agreement as the amount of data increases. We met a simple example of this in §11.6, when discussing the two urns, different initial odds converging to essentially equal odds with enough sampling from the urn. This is true rather generally in the Bayesian analysis, and scientists will ultimately agree, except for a few eccentrics; or else they accept that the model, or even the theory, is unsatisfactory. This is what happens in practice where a theory is initially a matter of dispute. At this stage, the science is subjective. Then the deniers collect data with a view to getting evidence against it, whereas the supporters experiment to see if the data support it. Eventually one side wins, with either the supporters admitting defeat, or the deniers accepting that they were wrong. In practice it is more complicated than these simple ideas suggest; for example, the theory may need substantial modification or be limited in its scope. Nevertheless, ultimately agreement will be reached and the subjectivity will be replaced by objectivity. Science is correctly viewed as objective when all but a few scientists agree. This can be seen happening now with climate change, though some of the skeptics are not scientists using Bayes, or other forms of inference, but groups who treat self-interest as more important than truth. A contrasting example is the geological theory of continental drift, which was for long not accepted but is now. Here, and in many other instances, data are not the only way to reach a definitive view of a theory; agreement can come through new ideas. In the case of continental drift, the new feature was an explanation of how the drift could happen.
Statisticians who reject the Bayesian approach, often for the reasons just discussed, still have probability as their principal tool but interpret it differently. The basic rules of convexity, addition and multiplication are used but thought of in a frequency sense (§7.2). Thus, the use of 
in a model with data x and parameter φ will be read as the frequency with which the value x will arise when the parameter has value φ. This view has substantial appeal when experiments are repeated in a laboratory, or when a sociologist records a quantity for each of a number of people. A consequence of this interpretation is that probability is only available for the data, never for the parameter, which is supposed to be fixed but unknown and cannot be repeated. We will refer to statistical methods based on this interpretation as frequency statistics. Most of the practical differences between the Bayesian and frequency views rest on the ubiquitous use of the likelihood principle by the former and its denial by the latter. There is even a frequency method called maximum likelihood that uses the likelihood function but denies the principle when it assesses how good is the result of using the method.
Nevertheless, the two attitudes do often, as with maximum likelihood, produce similar results, and practitioners of the frequency school have even been known to use a Bayesian interpretation of their results. For example, with a model of the type studied in the previous section with 
, a common frequency method is to provide a point estimate of φ, that is a function of the data x that is, in some sense, the most reasonable value for φ. In the method of maximum likelihood, the point estimate is that value of φ that maximizes the likelihood function 
for the data x observed. Often the point estimate is the posterior mean, or very close to it. In the normal case of the last section, the point estimate is the mean 
differing from the posterior mean only by the contribution from the prior, which will be negligible with a large amount of data. With many parameters, there can arise real differences between the results from the two approaches. An example was encountered in §9.10, where the apparently least-performing authority would have as its frequency point estimate the average over all relevant organizations within that authority, whereas the posterior expectation would be greater than that, and often substantially so, because of information about better-performing authorities.
In addition to point estimates, frequency methods use confidence intervals for φ, intervals in which they are confident the parameter really lies. The degree of confidence is expressed by a probability, namely the frequency with which the interval will include the true value on repetition of the procedure that produced the data. Again repetition replaces the Bayesian concept, repeats being with fixed φ. In interval estimation by maximum likelihood, the principle is denied. The violation of the likelihood principle is inevitable within the frequency viewpoint whenever uncertainty about a parameter is desired, since the only frequency probability concerns the data, the parameter being fixed but uncertain. Intervals of the posterior distribution can be used but they merely help interpret the inference, rather than being basic to it. Nevertheless, numerical agreement between the confidence and posterior intervals is often close, though gross discrepancies can arise.
One important way in which Bayesian and frequency views differ is in respect of “optional stopping”. Suppose two drugs are being compared to see which is more effective. Matched pairs of patients are treated, one with drug A, the other with drug B, to see which is better. Finance is available for 100 pairs but after 50 have been compared it is clear that drug A is superior to drug B. Under these circumstances, it seems sensible to stop the trials, partly for financial reasons, but more importantly because it is wrong to continue to give the inferior drug to 50 further patients. The trial is therefore stopped and the limited data used to make an inference and perhaps reach a decision. Statisticians have then asked themselves if the data from optional stopping needs to be analyzed differently from the analysis that would have been used had the trial started with resources for only 50 trials and the same results been obtained.
To examine this question, consider a situation in which the trial data form a Bernoulli series (§7.4) with chance θ of “success”, A being preferred to B, for each pair. In this context, consider two rules for terminating the series: in the first, the number n of trials is fixed; in the second, r is fixed, rather than n, and the series is halted when r successes have been observed. Suppose one experimenter fixes n, another fixes r, but that coincidentally the same results are obtained even down to the order of successes and failures. The relevant probability structures of the data are, for that with fixed n, 
, and with fixed r, 
.
The frequency method operates with the distribution of r in the first case, and n in the second, whereas the Bayesian needs only the observed values of r and n, using the likelihood 
as a function of 
, which is common to both experimental procedures. We have seen (§9.2) that in the first case, the distribution of r is binomial. The second distribution, whose details need not concern us here, is different. For example, with n = 6 and r = 2, we saw that the binomial extends from 0 to 6, whereas the other goes up from 2 without limit. It follows that the analyses within the frequency framework will be different for the two experiments, whereas the Bayesian, using only the likelihood, 
, will employ identical analyses. Readers who have encountered these problems before do not need to be reminded that the likelihood may be multiplied by any constant without affecting the Bayesian inference. This is clear from the discussion at the end of §9.1.
14.4 Significance Tests
The most obvious differences of real importance between Bayesian and frequency methods arise with significance tests that are now examined in more detail. A reader not familiar with these tests may wish to consult §11.10 before proceeding. As explained there, in the framework of a model 
, one value of 
may be of special interest. For example, the theory may imply a value for 
, as in the relativity experiment in §11.8, or if 
corresponds to the strength of a drug being tested, then 
implies that the drug is useless. It usually happens that the scientist thinks that the special value might obtain, in which case a Bayesian would assign positive probability to that event. We will suppose that special value to be zero. If, in the practical application, it was 
, redefine the parameter to be 
. Our Bayesian interpretation of the situation, thought by frequentists to require a significance test, will therefore be described by saying 
, where 
. Notice in the analysis of §14.2, when the parameter had a normal distribution, no value had positive probability since 
is the density and 
is the probability that 
lies in a small interval of width h that includes 
(§9.8). Within the Bayesian viewpoint, there are two classes of problem with any parameter that has a continuous range of values; in the first, the probability structure is defined by a density; in the second, there is a value of the parameter that has positive probability. It is the latter that gives rise to a significance test. The other case is sometimes referred to as a problem of estimation.
The particular significance test to be discussed has the same data structure as the estimation problem of §14.2, namely the data is a number x with model density 
with s known. This will enable comparisons to be made between the posterior appreciations in the two cases, of tests and of estimates. As already mentioned, 
. The prior distribution of 
when it is not zero remains to be specified and again it will be supposed to be the same as in the estimation case, 
centered on the value to be tested, with 
in the earlier notation. Centering it on the value 
to be tested means that, if not exactly 0, it is near to it, its nearness depending on t. It is usual to speak of the hypothesis H that 
. This leads to the complementary hypothesis 
that 
is not zero. We refer to a significance test, or simply a test, of the null hypothesis H that 
against the alternative 
that 
. In this language, the prior distribution 
is 
, the density of the parameter when the null hypothesis is false.
We are now in a position to use Bayes rule in its odds form (§6.5),
replacing F there by H, evidence E by x and omitting reference to background knowledge. Two of the terms on the right-hand side are immediate, 
and 
is 
, since under H, 
. It remains to calculate 
, which is done by extending the conversation from x to include 
, so that it consists of the sum, over 
, but excluding 
, of terms 
. The perceptive reader will query the omission of 
from the first probability, explained by the fact that, given 
, 
is irrelevant when 
. Unfortunately, this summation requires mathematics beyond the level of this book, so we must be content with stating the result, which is that x, with given 
, is again normal with zero mean and spread 
. This is another instance that makes normality so attractive. With both probabilities known, the likelihood ratio in (14.4) can be evaluated and the posterior odds found. These odds can be transformed into a posterior probability for H given x. It is this probability that we want to compare with the level of the significance test produced by frequency methods. Before doing this, we remark that, as in the estimation case of §14.2, we often have n data values, iid given 
. If so, the same result for the posterior odds persists with x replaced by the sample mean 
, which is still sufficient, and s by 
, using the square root rule (§9.5).
Recall that in a significance test, a small probability, usually denoted by α (alpha), is selected and if x departs significantly from the null value of the parameter, here zero, the result of the test is said to be significant at level α. In this sentence, “departs significantly” means that x falls in a region of values that, were H true, has probability α. The literature has extensive discussion as to how this region should be selected. Figure 11.1 illustrates the case where x is 
, where there is general agreement that the region is that shaded, where x differs from zero by more than a multiple of the spread s. We will take the case where α = 0.05, where the multiple is 1.96, effectively 2. If this happens, the frequency view says that the data are significant at 5%, suggesting that an unusual result (falling in the region) has occurred were H true, so that H is probably not true. Here the word “probably” is used in a colloquial sense and not with the exact meaning used in this book. In what follows, it is supposed that x, or 
, is significant at 5%, in that it differs from zero by 
, when we evaluate the posterior odds of H, given x or 
. One might hope that the frequency and Bayesian results would differ only a little, which would help to justify the near identification of “significant at 5%” with “posterior probability of 5%”, an identification that is sometimes made even by experienced statisticians, and is often made by people using elementary methods. As this is being written, a scientist, writing in a newspaper, does just this. In fact we show that the identification hardly ever exists, even approximately; the two views are entirely different.
Table 14.1 gives the numerical value of the likelihood ratio in (14.4) when t /s = 2 and 
is significant at 5%, for various values of n. It also gives your posterior probability 
when your prior value was ½, so that you originally thought that the null hypothesis had equal probabilities of being true or false. The most striking feature of Table 14.1 are the high values of your posterior probabilities; even when n = 1, it is a little over 33%. These are to be contrasted with the 5% significance, suggesting that H is not true. Your posterior values increase with n and even with n = 100, 74% is reached. It can be proved that with fixed significance level, here 5%, as n increases, your posterior probability will tend to one. In this situation, frequency ideas doubt the null hypothesis, whereas Bayes is nearly convinced that it is true. Here is a striking disagreement between the two schools of thought. The disagreement might be due to the particular prior used, though that is unlikely since other priors exhibit the same phenomenon. What is perhaps more serious is that, with a fixed significance level, here 5%, for different values of n, the posterior probabilities change. In this example, from 0.34 with n = 1, to any value up to the limit of one. This is an important illustration of incoherence, the phrase “significant at 5%” having different unacknowledged interpretations dependent on the number of observations that led to that level of significance. It is explained by the occurrence of the sample size, n, in the formula (14.5) below.
Table 14.1 The likelihood ratio and posterior probability, when x is 
, H is 
, 
, and 
is 
for n iid values giving mean 
that yields a significance of 5%
| n |  |
 |
| 1 | 0.480 | 0.341 |
| 5 | 0.736 | 0.424 |
| 10 | 0.983 | 0.496 |
| 50 | 2.097 | 0.677 |
| 100 | 2.947 | 0.742 |
The significance test is one of the oldest statistical techniques and has repeatedly been used when the number of observations is modest, rarely more than 100. More recently it has been used with large numbers, for example in studies of extrasensory perception. Within the last decade, the test has been used with vast amounts of data that need to be analyzed by a computer. An example that has been widely reported in the world's press is the data collected in the search for the Higgs boson. Since the posterior probability for the null in Table 14.1 tends toward one, it could happen that the Bayesian analysis differed substantially from the frequency result that appeared in the press. The reporting of the physics in the press has necessarily been slight, so that the physics may be all right but the statistics is doubtful. The eclectic view that sometimes frequency methods can be used, yet in others Bayesian methods are appropriate, is hard to defend. My own view is that significance tests, violating the likelihood principle and using transpose conditionals (§6.1), are incoherent and not sensible.
These calculations apply only to the selected numerical values but similar conclusions will be reached for other values. The more serious criticism lies in the choice of the appropriate prior when a significance test is used. As far as I am aware, there is no prior that gives even approximate agreement with the test for all values of n. There is another aspect of these tests that needs to be addressed. They are often employed in circumstances in which a decision has to be taken, so that inference alone is inadequate. There Bayes has the edge because his methods immediately pass over to decision analysis, as we have seen in Chapter 10, whereas a significance test does not. As an example of the misuse of tests, take a situation where it is desired to test whether a new drug is equivalent to a standard drug, perhaps because the new drug is much cheaper. This is called a test of bioequivalence. The experiment is modeled in terms of φ, the difference in potency of the two drugs, with φ = 0 as the null hypothesis H corresponding to bioequivalence. Often a significance test of H is used. This may be inadequate because ultimately a decision has to be made as to whether the new drug should be licensed. We have seen that this requires utility considerations (§10.2) leading to the maximization of expected utility (MEU). Omission of this aspect, as any inference does, would not reflect the operational situation adequately.
Finally, before we leave the critique of frequency statistics, and for the benefit of those who wish to extend the calculations given above, having at the same time, access to the exponential function, the formula for the likelihood ratio is provided. With the same notation as above, it is
where 
and 
. Notice that the individual spreads are irrelevant, only their ratio s /t matters. In Table 14.1, s /t = ½ and 
, corresponding to a significance level of 5%. Readers who would like to investigate the other two popular significance levels need 
for 1% and 
for 0.1%. Readers with a little familiarity with frequency statistics will recognize that two-tailed tests have been used throughout the discussion. The normal prior would be unsuitable for testing with a single tail, suggesting that 
. When n is large, the term 
, within the square brackets of the exponential function, can be ignored in comparison with the 1 there. Similarly, the 1 before 
in the square root can be ignored giving the good approximation
Consequently the likelihood ratio increases slowly with the square root of n for fixed significance level, which determines λ, and fixed 
. It is this dependence on n, the number of observations, that the tail area interpretation of the data ignores. 5% significance does not cast the same doubt on the null hypothesis for all n.
14.5 Betting
In most circumstances, the presence of uncertainty is a nuisance; we prefer to know the truth and act without the impediment of doubt. Nevertheless, there are circumstances where uncertainty is enjoyed, adding to the pleasure of an experience, at least for some people. Two examples were mentioned in §1.2: card games (Example 7) and horse racing (Example 8), both of which involve gambling, in the popular sense of that term. In our development of uncertainty, we have used the term “gamble” to describe all cases of uncertainty (§3.1). We now look at the recreation of gambling and recognize that there are at least two types, distinguished by whether the probabilities are commonly agreed by all, or very much dependent on the gambler. Roulette is an example of the former where everyone accepts that if the wheel has 37 slots, the probability of the ball entering any one slot is 1/37, at least in an honest casino when the gambler has no lucky number. Horse racing provides an illustration of the second type because punters have different views on which animal will win the race, placing their bets accordingly. Roulette and similar games are referred to as games of chance because they concern independent repetitions of a stable situation that can have two results, success or failure, as discussed in §7.8. The rules of probabilities were historically first developed in connection with games of chance, where current advances therein have used mathematics to provide valuable results, somewhat outside the scope of this book. Here we investigate betting, where chances do not arise because the conditions are not stable, one race being different in several ways from another. Our emphasis here will be on bets in horse racing, though betting occurs in other contexts too, for example football. It has even been claimed that one can bet on any uncertain event.
Here betting will be discussed primarily in connection with horse racing as practiced in Britain where, for a given race, each horse is assigned odds before running and payment is made to the punter according to the odds displayed at the time the bet is placed. The odds are commonly presented in the form exemplified by 8 to 1, which means that if the person placing the bet, the bettor or punter, stakes 1 cent on a horse at these odds, they will receive 8 cents, and have their stake returned if the horse wins; otherwise the stake is lost. The set of odds for all the horses running in a race is called a book, and the person stating the odds is called a bookmaker, who accepts the stakes and pays the successful bettors. Odds are always of the form r to 1, where r is a positive number, 8 in the illustration. Readers may find it helpful to think of r as the leading letter of the reward to the bettor. In our discussion, we find it useful to work in terms of rewards, rather than odds. Often it is useful to refer explicitly to the event E, the horse winning, and write 
. Since the racing fraternity abhors fractions, a bet at odds of 2½ to 1 will appear as 5 to 2. Odds such as 100 to 8, or 9 to 5 are not unknown. In writing, the word “to” is often replaced by a minus sign, thus 8−1 or 9−5, which can confuse. A mathematician would prefer to write simply 8, or 9/5 = 1.8. At this point the reader might like to reread §3.8, where odds were introduced in connection with Bayes rule, the relationship with probability was examined, and the distinction between odds against, used by bookmakers, and odds on as used in this book was made.
In §3.8, the odds on were defined for an event E in terms of probability as
in Equation (3.1). Had odds against been used, the ratio of probabilities would have been inverted to 
. It is therefore tempting to write
for the reward if the event E is true, that the selected horse wins the race. The temptation arises because the racing fraternity, and bettors generally, speak of “odds against” where we have used “reward”. It is often useful to do this and I personally prefer to turn the stated odds against into probabilities using the inverse of (14.6)
Thus, in this interpretation, odds against of 8 to 1 give a probability of 1/9 of the selected horse winning. However, while useful in some circumstances, the usage is dangerous because the left-hand side of (14.7) is not a probability; it does not satisfy the three basic rules, in particular the addition rule (§5.2). This result is now demonstrated for a race with only two runners but the argument is general and applies to realistic races with many runners, just as the addition rule extends to any number of events (§8.1).
Put yourself in the role of a potential bettor contemplating a two horse race in which the bookmaker has posted odds of 
to 1 and 
to 1, or in our terminology, rewards 
and 
for the two horses. The possibilities open to you are to place a stake of 
on the first horse and, simultaneously, stake 
on the second. Like the rewards, both stakes must be positive including zero, corresponding to not betting. Suppose you do this and the first horse wins, then you will be rewarded by 
but will lose your stake 
on the second horse, with an overall change in assets of 
. Similarly, if the second horse wins, the overall change is 
. At this point it occurs to you that perhaps, by judicious choice of the two stakes, it might be possible to make both changes positive; in other words, you win whatever horse wins. In the parlance of §10.5 you are on to a “sure thing”. Clearly no bookmaker could allow this, for he would lose money for sure. All he can control are the odds, or rewards, so we might ask whether he can prevent you being on to a sure win.
For you to have a sure win, both changes in assets have to be positive,
For this to happen, the ratio of your stakes must satisfy
The left-hand inequality follows from the previous left-hand inequality, and similarly the right-hand one. It follows that you can only find stakes that will give you a sure win if 
or equivalently 
; the product of the rewards (odds) must exceed one. The bookmaker would never allow this to happen since he could suffer sure loss against a wise punter if he did. He will always arrange for the product to be less than one. Recall that, from (14.6), 
where 
is the “probability” that the first horse wins, and similarly 
, so that the bookmaker must ensure that
Multiplying both sides of this inequality by 
and then subtracting this product from both sides reduces this to
We have two exclusive and exhaustive events—one and only one horse will win—so that if the p values were really probabilities, their sum would have to be one, in contradiction to (14.8). For a race with more than two horses, the extension of this result, which the readers can easily prove for themselves, is that the sum of the “probabilities” must exceed one to prevent a sure gain by a bettor. It follows that the left-hand sides of (14.7) cannot be termed probabilities. The reader may like to check this result for any book. As this is being written, a book is given for the result of a soccer match, with odds of 10 to 11 for a win by the home team, 3 to 1 for an away win, and 5 to 2 for a draw. The corresponding “probabilities” from (14.7) are 11/21, 1/4, and 2/7, adding to 1.06. The excess over one, here 0.06, determines the bookmaker's expected profit on the game.
An alternative expression for what has been established is that the bookmaker's odds cannot be a coherent expression of his beliefs about which horse will win the race. If not beliefs, what are they? They are numbers produced by the bookmaker that reflect the ideas of the people on the race course, or in betting shops, expressed in the stakes they have placed, and hopefully will give him the confidence to expect a profit.
We now turn to the behavior of the bettor when faced with a book for a race. The naïve approach is to look at what can be expected when a stake s is placed on a horse with reward r. If p is your, the bettor's, probability that the horse will win, then you have probability p of gaining rs and probability 1 − p of losing s, so that your overall expected (§9.3) gain is prs − (1 − p)s, which is equal to s times pr − (1 − p) = p (r + 1) − 1. You therefore expect to win if, and only if,
that is whenever your probability exceeds the bookmaker's “probability”, from (14.7). This can only happen with a few horses in the race since your probabilities coherently add to one, whereas the bookmaker's exceed one in total (14.8). Recognizing that the “probabilities” reflect the views of the crowd interested in the race, you should only bet, if at all, when your opinion of the horse is higher than that of the crowd.
The analysis in the last paragraph is not entirely satisfactory. One way to appreciate this is to study the expected gain, found above to be 
, which is positive if 
exceeds one, but then increases without limit with s, the stake. In other words, the naïve analysis says that if the bet is to your advantage, you should stake all of your assets. This is hardly sensible since, with probability (1 − p), this would result in your losing your stake and hence everything. The analysis is deficient for the reason discussed in §10.4, where it is shown that the proper procedure for the decision over whether or not to bet is to maximize your expected utility. The utility for money was discussed in §10.13, and it is also mentioned in connection with finance in §14.6. It was also emphasized that it is your assets that enter the consequences, or outcomes, at the end of the tree needed to decide what stake, if any, to place; so it is your utility for your assets that is required to make a rational decision, not gains or losses.
The correct analysis of a betting situation of the type we have been discussing involves three different sums of money: your initial assets c before making the bet, your assets if you lose, c − s, and those if you win, c + rs. With p still your probability of winning, you should place a stake that maximizes over s your expected utility
provided the maximum exceeds u (c). Here u (x) is your utility for assets x. To discuss this further would involve detailed consideration of the utility function, which needs more mathematics than the rest of this book requires, and would also need to include problems that do not involve uncertainty, the book's main topic. Readers still interested may like to refer to Chapter 5 of my earlier book, Making Decisions, Wiley (1985). One complication that can be mentioned is the recognition that betting on a horse race, or other sporting fixture, is not entirely a question of money. Most of us experience more enjoyment in watching a race if we have a bet on a horse, than if we do not. We enjoy cheering on High Street even though we may often suffer disappointment. If so, perhaps u (c + rs) in (14.9) should be increased to allow for the joy of winning, and u (c − s) decreased. Recall that utility refers to consequences and the consequences of a race include joy and disappointment.
14.6 Finance
There has been a serious deterioration in economic prosperity in the United States and much of Europe since the first edition of this book in 2006, a change that has affected most of the world. Capitalism has wobbled, the wobble being mainly due to unwise investments by some bankers. An investment is a procedure in which a sum of money is placed in a situation where it will hopefully increase in value but may decrease. The outcome is uncertain, in the same sense as that used in this book, and the final yield of the investment is an uncertain quantity (§9.2). Uncertainty is therefore at the heart of the economic downturn, so it is relevant to ask whether the bankers responsible have used the methods outlined in this book. Unfortunately, the activities of bankers are shrouded in mystery, so that even the most inquisitive of investigators, such as government regulators, do not know the details of what goes on in banks. Consequently it may be difficult, if not impossible, to know whether bankers used probability in a sound manner. However, it is possible to shed some light on the mystery of what goes on in investment houses.
Business schools at universities throughout the world teach students, some of whom enter the banking profession and handle investments. One is therefore able to gain some insight into what these former students might do by reading the textbooks used in their instruction. These books have become more sophisticated over the last 50 years, reporting on research done in that period, much of which employs undergraduate mathematics. It has also been noticed that many graduates in math, where they would previously have gone into manufacturing, gain lucrative employment with investment houses. Put these facts together and there is a possibility that some light can be shed on the follies of investors by studying the textbooks. This view is supported by at least two recent essays by academics in which it is claimed that the use of erudite mathematics, based on unsatisfactory models, which are not understood by senior bankers, has contributed to the economic collapse. Let us then look at the methods described in the popular textbooks on finance.
When this is done, it soon becomes apparent that all the methods considered are based on an assumption that people, in particular bankers, are rational, whatever that means in an uncertain situation. Our thesis is based on coherence (§§3.5 and 13.3), which essentially means that all your activities fit together, like pieces in a well-made jigsaw, and that you will never experience two activities clashing, like pieces not fitting tightly, and where you would be embarrassed by having to admit an error. It came as a surprise to me when the books were examined, that there is rarely any reference to coherence, and the concept of probability is not adequately explored. A close examination shows that the methods, developed in detail and with powerful mathematics, are incoherent. In other words, in direct answer to our question above concerning the methods used by bankers, we can say that many of them are deficient in this respect. It is easy to demonstrate such incoherence; indeed it was first done in 1969 and the writing subsequently ignored. We now pass to a simple proof that one popular method is incoherent, using ideas developed in Chapter 9, especially §9.5.
An investment consists of an amount of money, placed in an activity now, in the anticipation that at some fixed time in the future, say a year, it will have increased in value, recognizing that it may alternatively decrease. The value of the money after a year will be termed the yield of the investment. We denote it by the Greek letter (§11.4) theta θ. At the time the investment is made, θ is an uncertain quantity for you, the investor. In the discussion that follows, the reader might find it useful to take the case of betting (§14.5), where a stake is invested in the outcome of an uncertain event such as a horse race. If the event occurs, the horse wins, then you have a reward and your stake is returned. If the contrary happens, you lose your stake. Here θ takes only two values, which are known to you at the time the bet is placed, at least when the odds are fixed. Thus, a 1dollar stake at 10−1 against will yield either 10 dollars or lose 1 dollar. This case, where θ takes only two values, will suffice to demonstrate incoherence of some, even most, textbook methods.
Returning to the general case, θ will have a distribution for you at the time the investment is made. As you will have appreciated from Chapter 9, a distribution is a complex idea involving many probabilities, so that it is natural to simplify the situation in some way. The obvious way is to consider the expectation of the investment or, what is usually called in this context, the mean yield (§9.3). Thus, in the example just mentioned, the mean is 10p − 1(1 − p), where p is your probability, at the time you place the bet, that the chosen horse will win. This is only positive if p exceeds 1/11 and you might only place the bet if this held; that is, if your mean was positive and you expected to win. (Recall that p is your probability, not the bookmaker's (§14.5)). We have, at several places in this book, argued in favor of simplicity but the idea of replacing a whole distribution by its mean is carrying simplicity too far. There is another feature of a distribution that is usually relevant, namely the spread (§9.5) of θ. If the stake in the example is increased from 1 to 10 dollars, the mean is still positive and the bet worthwhile if p exceeds 1/11, but the spread is greater, the distribution ranging from −10 to +100. As a result, the bet may be thought sensible at a dollar stake but reckless at 10 dollars, especially if the latter is your total capital. Investors in the stock market can feel this, often preferring government stocks with a guaranteed yield, zero spread, to risky ventures that might do well but might lose them a lot of money, large spread. Utility considerations could be relevant here.
Considerations such as these lead to many methods in the financial textbooks replacing the distribution of θ, many numbers, by just two, the mean and the spread of θ. The spread is usually measured by the standard deviation (§9.5) but for our immediate purposes, it will not be necessary to discuss how it is calculated. With the problem of investment reduced from consideration of a whole distribution to just two numbers, the solution is much simpler and real progress can be made. We now argue that this is simplicity gone too far, with possible incoherence as a result. This incoherence is now demonstrated and only afterward will we return to an alternative specification that is not so simple but is coherent.
With both mean and spread to work with, the investor wishes to increase the mean but decrease the spread. Government stocks achieve the latter but have lower expectations than risky securities. A scenario like this has been met before (§10.13) where two different features were discussed, your health and your assets. It was found convenient to represent the situation by a Figure (10.6) with assets as the horizontal axis and health as the vertical one. Here in Figure 14.1, we do the same thing with the spread horizontal and the mean vertical. As in the earlier figure, curves are drawn such that all the values of the combination (assets, health) on a single curve are judged equivalent, any increase in health being balanced by a decrease in assets. There we wanted to increase both quantities, assets and health; here one desires an increase in mean but a decrease in spread, so the curves of spread and mean are differently placed, going from southwest to northeast in Figure 14.1. Consider points A and B on one of these curves. A corresponds to an investment with zero spread, whereas B corresponds to an investment with larger mean, giving it an advantage, but is disliked for its larger spread. That A and B are on the same curve means that the two investments are of equal merit, the increase in spread in passing from A to B being balanced by the increase in mean. (Notice that the curves in Figure 10.6 were of constant utility. Here the curves are merely those where all points are judged equivalent. We will return to utility in connection with investments below.) We now show that the use of these curves to solve an investment problem leads to incoherence.
Figure 14.1 Curves of equal merit in an investment.
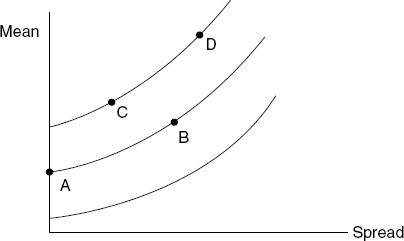
Suppose that you have settled on the curves in Figure (14.1) and, in particular, decided that an investment with mean 2 and spread 6 (C in the figure) is as good as one with mean 4 and spread 10 (D in the figure), the undesirable increase in spread in passing from C to D balanced by the increase in mean. Recall that it is being supposed that in evaluating investments, only mean and spread matter. We now produce two investments that correspond to C and D but in which D is obviously the better. It would not be an exaggeration to say that it is nonsense to judge the two investments, C and D, equal; the polite word is incoherent. The two investments are of the type described above.
C corresponds to placing a stake of 1 on a bet at odds of 5−1 against, where you have probability ½ of winning. D has odds of 9−1 against but otherwise is the same as C. It is immediate that
The means are obvious. For C it is −1·½ + 5·½ = 2 (§9.3 where it is referred to as expectation); similarly, for D it is −1·½ + 9·½ = 4. The spread, in the familiar use of that term, is the difference between the higher and lower values that are possible, 4 for C, 6 for D. (Readers comfortable with the term standard deviation may like to be reminded that the measure of spread used here is twice the standard deviation, the factor 2 being irrelevant in this context.)
Now for the crunch: despite your rather sophisticated judgment in Figure (14.1) that C and D are equivalent, it is now obvious that D is better than C. In both bets, you stand to lose 1 with probability ½, whereas your winnings would be 5 with C but a better 9 with D, again with the same probability of ½. Everyone prefers D to C.
The approach used here with a numerical example can be generalized. If an investment with one pair of mean and spread is judged equivalent to a different pair, then two bets, each with the same means and spreads, can always be found in which one bet is blatantly superior to the other, so denying the sophisticated judgment of equivalence. The conclusion has to be that the comparison of investments solely through their means (expectations) and spreads (standard deviations) is unsound. It is surprising that so much effort has been put into methods based on an erroneous assumption. If these have been used in practice, then surprise turns to disquiet.
My own view is that this erroneous assumption could not, on its own, have led to the bankers acting as they did. It is true that many of the investments considered by them were difficult to understand but it is unlikely that this misunderstanding was enhanced by the use of mean–spread methods; rather the complexity of the methods may have disguised the nature of the investments. Another consideration is that, in practice, the erroneous methods may be good approximations to coherent, or even rational procedures. No, we need to look elsewhere for a convincing explanation for the credit crunch and recession.
A possible explanation can be found by going beyond the appreciation of the investment through the yield, θ, with your associated distribution of θ, to a recognition that to be effective, a decision has to be made about whether the investment should be taken and, if so, how much should be invested, the stake in the betting example. In other words, an investment is not just an opinion, it involves action. Bankers correctly refer to investment decisions and it is necessary to go beyond uncertainty, expressed through probability, to actions (§10.1). We have seen that doing this involves an additional ingredient, your utility (§10.2). Specifically, you need both a distribution (of probability) and a utility for the consequences of your actions in investing. Bankers should have had their utility function in mind when they acted, and should have then combined it with the distribution to enable them to decide by maximizing expected utility (MEU, §10.4). So a legitimate question that might be asked is, what utility function do bankers use? Or, since like the textbooks, little if any mention is made of utility in banking, perhaps the question needs modification to ask what utility should be used?
Bankers deal in money, so it is natural to think in terms of utility as a function of money. This was briefly discussed in §10.13 and a possible form of utility as a function of assets was provided in Figure 10.7. There the point was made that the money referred to had to be your, or the bank's, total assets. Thus, in investment C above, expressed as a bet, were your assets when contemplating the bet 100 dollars, you would need to consider assets of 99 dollars were you to lose, and 105 dollars were you to win. The increases of 100 dollars do not affect the argument used there but clearly, with the utility of Figure 10.7 in mind, investment C with assets of 1 dollar would be viewed differently with assets of 100 dollars, if only because in the former case, you might lose everything, whereas in the latter, a drop from 100 dollars to 99 dollars matters little.
Would it be sensible for bankers to consider their utility solely as a function of money? It might be provided it had the form of Figure 10.7 and the assets were the bank's, rather than those of individual bankers. For, if many investments failed together, the bank's assets would drop to near zero and the bank could fail. So perhaps they did not have a utility like that. Yet on the other hand, if the assets were those of an individual banker, the curve could account for the enormous bonuses they took. A glance at Figure 10.7 shows that a rich person needs a large increase in assets to achieve a small gain in utility, as can be seen by comparing the passage from Q to P with that from B to A. We just do not know if bankers had any utility in mind, and if they did, what form it took.
We might question whether the coherent banker should have a utility that depends solely on money, expressed either in terms of their own money or the combined assets of the bank. Consider the offer of a mortgage on a property. If the mortgagor fails, the bank will still have the property but the mortgagor may suffer what is to them a serious loss. Should the bank incorporate this serious loss into their utility? Should their utility involve more than their assets? My personal view is that bankers, like all of us, are social animals and should base their decisions on the effects they might have on society, on you and me. I strongly believe that bankers should have seriously discussed social issues that might have been affected by their actions. Only then should they have maximized the expected utility. What little evidence we have, through bankers being grilled by politicians, suggests that social utility did not enter into their calculations.
Of course, it is not only the bankers whose activities influence society. Pharmaceutical companies appear not to take adequate account of people either in choice of what drug to develop or in the prices they charge. Generally, commercial confidentiality, at the basis of capitalism, hides the motives behind management, so that we do not know whether big companies employ utility concepts, or if they do, what factors they take into consideration. Perhaps only the shareholders are considered.
It would appear from the textbooks on management and finance that the concept of utility is not used despite the demonstration that it, combined with probability, upon which it is based, giving MEU, provides coherent decisions. There are two reasons for this. First, the issue of confidentiality: decision makers would be embarrassed by a public demonstration of their utilities. The second reason is the hostility of so many people to the measurement of abstract concepts such as happiness. They either fail to appreciate the power of numbers in their ability to combine easily in two different ways (§3.1), or they fail to recognize what it is that we are trying to measure. Utility is a measure of the worth to you of a consequence or an outcome (§10.2). No attempt is made to measure happiness, rather to measure your evaluation of some real outcome, which may involve an abstract idea, like happiness, in a material circumstance. All the measurements proposed here depend on the measurement of probability, which is discussed in Chapter 13 and the ideas developed there leave much to be desired, so that serious research on the topic needs to be done. Rather than award a Nobel Prize to someone who correctly shows how bad we are at decision making, we should support research into coherent decision making.
A wider issue here is the question of privacy. By suggesting that a company should provide us with its utility function, we are effectively invading its privacy. Indeed, whenever we ask for utilities in decisions that have social consequences, we are posing questions of privacy. My personal opinion is that the reasoning used in this book, leading to MEU, leads to the denial of privacy except in decisions that affect only the decision maker. Such questions are rare. For example, I think, as a result of MEU being the preferred method of decision making, all tax returns should be available online. It should significantly reduce tax avoidance and perhaps even tax evasion. Privacy is a quality endorsed by bad people so that they can do bad things.