Chapter 4
Operational Safety Decision-making and Economics
4.1 Economic Theories and Safety Decisions
4.1.1 Introduction
Making a decision is often difficult because of the uncertainties involved and the risks these uncertainties entail. A balance needs to be struck between different alternatives and the corresponding consequences. The decision therefore depends in part on how a choice problem is defined and the value that is attached to the pros and cons of an alternative. However, this involves a lot of uncertainty, as people can never be completely sure of the exact consequences of the chosen course of action [1].
Much research on decision-making has already been carried out in different disciplines. Various models and theories can be found in the literature that describe decision-making under conditions of uncertainty and which attempt to explain the phenomena observed. The first theory, developed as early as the seventeenth century, is the “expected value theory” (see also Chapter 2). According to this theory, people take decisions by maximizing the expected value.
However, the St. Petersburg paradox – which is a paradox related to probability and decision theory – made it clear that the expected value theory would not hold in real situations. The paradox is based on a particular (theoretical) lottery game that leads to a random variable with an infinite expected value (i.e., infinite expected payoff) but that nevertheless seems to be worth only a very small amount to the participants. The St. Petersburg paradox is a situation where a naïve decision criterion, which takes only the expected value into account, predicts a course of action that no actual person would be willing to take (see also Section 4.1.2). The St. Petersburg paradox therefore made a more accurate model necessary, and Bernoulli developed a new theory, the “expected utility theory.” This theory states that people attempt to maximize not the expected value, but the expected utility, when making decisions (see also Chapters 3, 7, and 8). People assess the utility of each outcome based on probabilities and then choose the alternative with the highest sum of weighted outcomes.
Kahneman and Tversky then developed a theory that took into account the human factor: the “prospect theory.” This theory was very successful as it included the psychological aspects of human behavior. In this theory, a choice problem is defined relative to a reference point. Depending on coding in terms of gains and losses, people will show more risk-averse or risk-seeking behavior [2–5].
People are constantly taking decisions, consciously or unconsciously. It is therefore not surprising that the subject of decision-making is studied in various disciplines, from mathematics and statistics to economy and political science, to sociology and psychology.
4.1.2 Expected Utility Theory
As described in the introduction, the first universally applicable decision-making theory was the “expected value theory,” developed as early as the seventeenth century. According to this theory, people take decisions based on maximization of the expected (monetary) value. However, this theory was repudiated by the St. Petersburg paradox. In the St. Petersburg paradox, a coin is tossed until “heads” appears. If “heads” appears on the first toss, the casino pays €1, otherwise it doubles the payout each time “heads” appears. What price would you be prepared to pay to enter this game? This paradox describes a gamble with an infinite expected value. Even so, most people intuitively feel that they should not pay a large price to take part in the game [3, 6].
To solve the St. Petersburg paradox, Bernoulli developed a new theory. He suggested that people want to maximize not the expected value, but the expected utility. As a result, the utility of wealth is not linear, but concave. After all, an increase in wealth of €1000 is worth more if the initial wealth is lower (e.g., from €0 to €1000) than if it is higher (e.g., from €10 000 to €11 000). This theory is called the expected utility theory in the literature. It is a theory about decision-making under conditions of risk in which each alternative results in a set of possible outcomes and in which the probability of each outcome is known. Individuals attempt to maximize the expected utility in their risky choices. They calculate the utility of each outcome using probabilities and choose the alternative with the highest sum of weighted outcomes. The attitude of an individual to risk is defined by the form of a utility function. For a risk-averse individual, the function is concave; for a risk-neutral individual, the function is linear; and for a risk-seeking individual, the function is convex. Given a choice between a certain outcome with a utility y and a gamble with the same utility y, a risk-averse individual will choose a certain outcome, a risk-seeking individual the gamble, and a risk-neutral individual will treat the two outcomes equally [3–5, 7–9].
4.1.3 Prospect Theory
The expected utility theory has been considered for a long time the most applicable method but, despite its strengths, it has encountered several problems as a descriptive model for decision-making under conditions of risk and uncertainty. After all, it requires that the decision-maker has access to all the information describing the whole of the situation. Clearly, this information requirement is far too rigorous for most practical applications, in which the probabilities cannot be calculated exactly, or the decision-maker does not yet know what he or she wants, or the series of alternatives is not fully determined, and so on. In addition, there is plenty of experimental evidence to suggest that individuals often fail to behave in the manner defined in the expected utility theory. In fact, the choices made by individuals consistently deviate from those predicted by the model, as is made clear in the experiments of Allais and Ellsberg.1 The so-called Allais paradox shows that individuals are sensitive to differences in probabilities. Experiments show that an individual's willingness to choose an uncertain outcome depends not only on the level of the uncertainty, but also on the source. People show dependence on a source when they are prepared to choose a proposition from source A but not the same proposition from source B. Regarding the so-called Ellsberg paradox, there are different versions of Ellsberg's experiment. In one version there are two urns, one containing 50 black and 50 red balls, and the other containing 100 balls about which it is only known that they are either red or black. People must choose an urn and a color, then draw a ball from the chosen urn. If the ball matches the color chosen, the subject wins a prize. Ellsberg noted that people display a strong preference for the urn with an equal number of red and black balls, despite the fact that economic analysis suggests that there is no reason to prefer one urn or the other. Ellsberg's classic study therefore shows that people attach a higher value to bets with known probabilities (risk) than to bets with unknown probabilities (uncertainty). This preference is called “ambiguity aversion.” The Ellsberg experiment shows that it is possible that decision-makers will not follow the usual rules of probability if they cannot act based on subjective probability. As a result, in such situations the theory of expected utility does not accurately predict behavior. For a more positive appreciation of expected utility theory see Chapter 7. An alternative theory was therefore required to describe the observed empirical deviations [3–5, 7–20].
Kahneman and Tversky's [4] prospect theory is considered an alternative to the expected utility theory and one of the principal theories for decision-making under conditions of risk. According to this theory, individuals are more likely to assess outcomes based on change from a reference point than on an intrinsic value. After all, people tend to think in terms of losses and gains rather than intrinsic values and therefore make choices based on changes relative to a certain reference point. The reference point is often, but not always, the status quo. Assuming that the reference point is zero, gains are represented by positive outcomes and losses by negative outcomes. The concept of a reference point means that people deal with losses differently from gains. Because people code outcomes in terms of a reference point and deal with losses and gains differently, the definition of this reference point or construction of the choice problem is crucial. How people approach the problem – i.e., in terms of losses or gains – affects the preferences independently of the mathematical equality between the two choice problems. Most decision problems take the form of a choice between maintaining the status quo and accepting an alternative, which may be more advantageous in some respects and less advantageous in others. The advantages of an outcome are then assessed as gains and the disadvantages as losses. Individuals usually give more weight to losses than to comparable gains and display more risk-averse behavior in the case of gains and more risk-seeking behavior in the case of losses [2–5, 10, 21–28].
According to prospect theory, each individual attempts to maximize the utility function, defined not in absolute terms but in terms of losses and gains relative to a reference point. This function is usually concave for gains and convex for losses, reflecting the risk-averse behavior for gains and risk-seeking behavior for losses, as shown in Figure 4.1 [2, 3, 8, 10, 21, 24, 27–30].

Figure 4.1 Utility function of prospect theory.
(Source: Wikipedia, 2016 [31].)
Risk-averse behavior for gains is seen in the fact that people choose certain gains rather than uncertain, but larger, gains. In Figure 4.2, a certain gain is shown as CE and the uncertain, larger, gain as x*. Due to risk-averse behavior, the expected value of the uncertain gain E[U(x)] is lower than the actual utility for this gain U(x*). The utility function of a risk-averse individual is therefore concave. Risk-seeking behavior in the case of losses, on the other hand, is expressed by the fact that people choose uncertain, higher losses rather than certain, but lower losses. Finally, in the case of risk-neutral behavior, the expected value, E[U(x)], will be equal to the actual utility U(x*), and the utility function will be linear. These findings can be readily applied to operational safety by inserting the safety utility function Su in the place of the utility function (see also Figure 3.6).
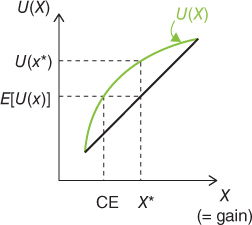
Figure 4.2 Utility function for gains (risk-averse behavior).
These findings show that the preference for prospects relating to losses only are the mirror image of preference for prospects relating to gains only. Kahneman and Tversky [4] call this the “reflection effect” around the reference point. This means that the sensitivity to change decreases with increasing distance from the reference point [2, 3, 8, 10, 21, 24, 27–30].
An aversion to risk is reflected in the observed behavior, i.e., people are more sensitive to losses than to gains. The utility function for losses is therefore steeper than that for gains, as shown in Figure 4.3. A loss of €5000 results in a value of −€4000, whereas a gain of €5000 only results in a value of €3000. In absolute terms, therefore, people attach a higher value to a loss than to an equivalent gain. This means that a reduction in loss has a much higher value than an increase in gain of the same amount, so that people express more risk-seeking behavior in the case of losses and more risk-averse behavior in the case of gains. The convex curve for losses and concave curve for gains therefore give a typical utility function an S-form [2, 3, 8, 10, 21, 24, 27–30].

Figure 4.3 The utility function curve.
(Source: Reproduced with permission of LessWrong [32].)
People treat gains differently from losses based on two aspects. The first of these is the reflection effect, as discussed earlier, and the second is “loss aversion.” Loss aversion explains why losses weigh more heavily than gains. It implies that people prefer the status quo, or other reference point, to a 50/50 chance of positive and negative alternatives with the same absolute value. The negative utility of giving up a good is therefore experienced as greater than the utility of acquiring a good, so that people often choose the status quo rather than a change. This phenomenon reflects the observed greater sensitivity to losses than to gains. The result is a utility function that is steeper for losses than for gains. One implication of loss aversion is that individuals have a strong tendency to remain in the status quo, as the disadvantages of leaving the status quo weigh more heavily than the advantages. Loss aversion also implies that people place a higher value on a good that they own than on a similar good that they do not own. This overvaluing of property is called the “endowment effect.” The process of acquiring a good increases its value. This even applies to trivial goods such as sweets or coffee mugs. One consequence of this phenomenon is that people often ask for more to give up a good than they are prepared to pay for it. This means that the selling price is always higher than the buying price, as the highest price a buyer is prepared to pay to acquire a good will be lower than the minimum compensation required to give up the same good [2, 4, 5, 10, 21, 24, 26–28, 33–36]. Translated into safety language, this means that safety management is not inclined to change existing company safety measures and policies, even if the new safety measures and policies would prove to be better at the same price. Therefore, a minimum safety increase premium (see Section 4.2.5) may be needed to convince safety management to change an existing safety situation.
In addition to the reflection effect, loss aversion, and the endowment effect, the prospect theory also makes use of other effects to describe and explain behavior during decision-making processes. First of all, it is possible to deduce from a number of empirical observations that individuals weigh certain outcomes more heavily than possible outcomes. This is called the “certainty effect.” People also weigh small probabilities more heavily, and attach too little weight to average and high probabilities. As a result, highly probable but uncertain outcomes are often treated as if they were certain. This effect is called the “pseudo-certainty effect.” Consequently, changes in probability that approach 0 or 1 have a larger impact on preferences than comparable changes in the middle of the range of probability. This effect can be clarified using the following example: during a hypothetical game of Russian roulette, people are prepared to pay more to reduce the number of bullets in the revolver from one to zero than from four to three. There is also the “immediacy effect,” which refers to a preference for outcomes that are experienced immediately. Finally, prospect theory also describes a “magnitude effect.” This effect refers to the following pattern: people are risk-seeking in the case of small gains and become strongly risk-averse as the size of the gain increases, and people are risk-averse in the case of very small losses and become more risk-seeking as the size of the losses increases [5, 8, 10, 21, 24, 25, 27].
4.1.4 Bayesian Decision Theory
The Bayesian decision theory can be seen as the newest theory, further advancing insights beyond prospect theory, and aims to resolve the consistency problems with, on the one hand, predictive risk analysis and expected utility theory and, on the other, common-sense considerations of risk acceptability in some well-constructed counter-examples in experiments like the ones by Allais and Ellsberg which are typically brought forth by the behavioral economists. This neo-Bernoullian decision theory is a direct reaction to Kahneman and Tversky's prospect theory [27], which was felt to put too high a premium on the sterile empiricism of hypothetical betting experiments, while at the same time failing to appeal to the need for compelling and rational first principles. The Bayesian decision theory differs from the expected utility theory in that an alternative position measure which captures the worst-case, most likely, and best-case scenarios is maximized, rather than the traditional criterion of choice where the expected values are maximized.
It can be demonstrated that this simple adjustment of the criterion of choice accommodates (non-trivially) the Allais paradox and the common-sense observation that type II events are more risky than type I events, as well as (very trivially, as the Ellsberg paradox is arguably not that paradoxical) the Ellsberg paradox (see Sections 7.3 and 7.4, respectively). Moreover, it can be shown that the proposed alternative criterion of choice relative to the traditional criterion of choice leads to a more realistic estimation of hypothetical benefits of type II risk barriers (see Section 8.12).
4.1.5 Risk and Uncertainty
The world that we live in is a world full of uncertainties in which, in most cases, we are unable to predict future events. Nevertheless, people are forced to make predictions given that suitable management responses are required when facing uncertainties, particularly in the field of operational safety. To explain how people deal with uncertainty when making a choice between different alternatives, use has traditionally been made of either formal models or rational analyses. Two types of models are used. The first of these is used mainly in economics and in research into decision-making: a numerical value is assigned to each alternative and the choice characterized by maximization of this value. In doing this, people mainly make use of normative models, such as the expected utility theory, or descriptive models, such as the prospect theory. The second type of model is usually used in law and politics. This approach identifies different reasons and arguments for why a certain decision should be taken. When making a decision, people weigh up the reasons for and the reasons against a certain alternative. A decision therefore depends in part on the value attached to the pros and cons of a particular alternative [1, 37].
A distinction should be made between “uncertainty” and “(negative) risk.” The difference between risk and uncertainty is that, in the case of uncertainty, the probability is not fully known. Risk is characterized by an objective probability distribution, while uncertainty bears no relation to statistical analysis [5, 38, 39].
In the modern world, (negative) risk takes two fundamental forms. Risk as a feeling refers to the quick, instinctive, and intuitive response of an individual to danger. Risk as analysis results in logic, reasoning, and scientific deliberation, as applied in risk management. People generally make decisions involving risk by constructing qualitative arguments that support their choice. During a decision-making process, a distinction is made between risky and risk-free choices. Risky choices are made with no prior knowledge of the consequences. As the consequences of such actions depend on uncertainties, this choice can also be regarded as a kind of gamble that results in certain outcomes with varying probabilities. However, the same choice can be described in different ways. For example, the possible outcomes of a gamble can be described as gains and losses compared with the status quo or the initial position. An example of decision-making involving risk is the acceptability of a gamble that results in a certain monetary outcome with a specific chance. A typical risk-free decision concerns the acceptability of a transaction in which a good or service is exchanged for money or labor. Most people will choose certainty in preference to a gamble, even though a gamble has, mathematically speaking, a higher expected value. This preference for certainty is an example of risk-averse behavior. As indicated before, a general preference for certainty rather than a gamble with a higher expected value is called risk aversion, and rejection of certainty for a gamble with the same or a lower expected value is called risk-seeking behavior. Furthermore, as also previously mentioned, people usually display risk-averse behavior when faced with improbable gains and risk-seeking behavior when faced with improbable losses [4, 38–41].
In addition to decision-making under conditions of risk, decision-making under conditions of uncertainty is also possible. Uncertainty describes a situation in which the decision-maker does not have access to any required statistical information. Various definitions of uncertainty are given in the literature. Whichever definition is used, uncertainty is not static, due to the dependence on knowledge. For example, if the amount of available information increases, the uncertainty will be reduced (e.g., going from domain B toward domain D in Figure 2.5). The term uncertainty is mainly used to describe the uncertainty resulting from the consequences of actions that are unknown because of their dependence on future events. This is often called “external uncertainty,” as it concerns the uncertainty of ambient conditions beyond the control of the decision-maker. Internal uncertainty refers to uncertainties in the preferences of the decision-maker, the definition of the problem, and the vagueness of the information [38, 42–50].
There are in fact two types of uncertainty – objective and subjective. Objective uncertainty relates to the information about the probabilities, whereas subjective uncertainty relates to the attitude of the decision-maker. There are two aspects with respect to this attitude of decision-makers: their attitude to the gain and their attitude to the negative risk. The attitude of a person to risk is traditionally – in accordance with expected utility theory – defined in terms of marginal utility or the form of the utility function. If a decision-maker is not risk-neutral, then the subjective and objective probabilities will not be equal [5, 49].
Decision-making under conditions of uncertainty takes place either if the prior information is incomplete or if the outcomes of the decisions are unclear. The best strategy for dealing with uncertainty in decision-making is to reduce or completely remove this uncertainty. Uncertainty can be reduced by collecting more information before making a decision or by delaying a decision. If no further information is available, uncertainty can be reduced by extrapolating the available information. Statistical techniques can be used to predict the future based on information relating to current or past events. Another technique is to form assumptions. Assumptions enable experienced decision-makers to take quick and efficient action within their domain of expertise, even if there is a lack of information. If it is considered to be unfeasible or overly expensive to reduce the uncertainty, this uncertainty can be acknowledged in two ways: by taking it into account when selecting an alternative, or by preparing to avoid or face the possible risk involved [42, 46, 48, 50].
If a decision is to be made under conditions of uncertainty, use can be made of various decision strategies, including MaxMin strategy, MaxMax strategy, and the Hurwicz criterion strategy. The choice of model depends on the attitude of the decision-maker. Three different attitudes are described in the literature: pessimistic, optimistic, and neutral. In the case of a pessimistic attitude, the decision-maker only considers the worst case for each alternative. He therefore makes use of the MaxMin strategy, and the alternative with the highest gain in the worst case will be selected. In the case of an optimistic attitude, decision-makers only consider the best case for each alternative. They therefore select the alternative with the highest gain in the best case, using the so-called MaxMax strategy (not to be confused with the so-called “Maxmax hypothetical benefits” – see later in this chapter). The third type is the neutral attitude. In this case, the decision-maker considers each case in the same way and the evaluation value of each alternative is determined by the general conditions. A combination of an optimistic and pessimistic attitude is called the Hurwicz method [45, 47, 49].
It should be noted that the uncertainties involved in making decisions increase in size and impact if decisions need to be made concerning the risks related to type II risks. After all, high-impact, low-probability (HILP) events are characterized by low probabilities and large, extensive, and possibly irreversible consequences. Type II risks are not always well understood, with the result that people do not always know how to deal with them. It is not possible to increase knowledge through experimentation, given that the risks are effectively irreversible in a normal time frame. The classic theories, based on expected utility, therefore do not always work and results should be interpreted with great caution, as the models tend to underestimate events with low probabilities [46, 51], as is demonstrated in Section 7.5.
4.1.6 Making a Choice Out of a Set of Options
When making a decision, a choice usually needs to be made from a set of possible options. This choice is not made randomly. An attempt is made to make a choice that provides the best answer to a number of criteria: the optimum choice. Each choice results in a gain of a certain value, so that the choice is selected with the largest gain. However, in most cases, the gains resulting from a choice are affected by variables of unknown value. It is traditional to assume that, if a rational choice needs to be made between two alternatives that involve uncertainties, the uncertainty is described using probability and the different alternatives are ordered based on the expected utility of the consequences of these alternatives. Selection of one alternative is therefore based on the probability and potential value of a possible outcome [47, 52, 53].
There are two phases involved in making a choice. The first phase involves various mental operations that simplify the choice problem by transforming the representation of outcomes and probabilities. Coding involves the identification of the reference point and the framing of outcomes as deviations from this reference point, and this affects orientation toward risk. After all, a difference between two alternatives will always have a larger impact if it is seen as a difference between two disadvantages rather than a difference between two advantages. The decision can therefore be made to allow the disadvantages of a deviation to weigh more heavily than the advantages. In addition, common elements to the various alternatives or irrelevant alternatives are also often eliminated. This “isolation effect” can result in different preferences, as there are different ways of separating prospects into shared and distinctive elements. This can result in a reversal in preferences and inconsistency. The second phase is the evaluation phase [5, 36].
The traditional utility function assumes that an individual has a well-organized and stable system of preferences and good calculation skills. However, such an assumption is unrealistic in many contexts. In response to this problem, Simon [54] developed the theory of bounded rationality. This implies that, due to the expense and impracticalities involved in choosing between all possible alternatives to achieve the optimum choice, people usually look for the first satisfactory alternative that meets a set of predetermined objectives. The implication is therefore that human behavior should be modeled as satisfying rather than optimizing. Such an approach has several appealing qualities, as working with objectives is, in most cases, very natural [47, 54, 55].
Evaluation of the outcomes is susceptible to framing effects due to the non-linear utility function and people's tendency to compare outcomes with a reference point. The decision frame used to analyze a decision refers to the perception of the decision-maker regarding a possible outcome of a risky decision in terms of gains and losses. Whether or not a certain outcome is seen as a loss or a gain depends on the reference point used to evaluate possible outcomes. The framing effect is seen whenever the same outcome can be considered a loss or a gain, depending on the reference point used. For example, if a company is faced with an accident cost of €5000, which was expected to be €10 000, is this experienced as a loss or a gain? The answer depends, for example, on whether the previous accident cost or the expected value is used as a reference point. Whether or not a decision is considered in terms of a loss or a gain is very important, because people display risk-seeking behavior when faced with losses and more risk-averse behavior when faced with gains [4, 8, 56].
It is therefore clear that emotions play an important role in social and economic decision-making. Individuals, including people who need to make decisions on safety budgets – such as safety managers and middle and top managers – evaluate alternatives subjectively and emotions influence these evaluations. People generally try to control these emotions and to anticipate the emotional impact on future decisions, as emotions can affect such decisions. The impact of emotions is of particular importance when assigning a value to different perspectives [8, 57].
4.1.7 Impact of Affect and Emotion in the Process of Making a Choice between Alternatives
Traditional economic theory assumes that most decision-making involves the rational maximization of the expected utility. Such an approach assumes that people have access to unlimited knowledge, time, and information-processing skills. In the 1970s and 1980s, researchers identified several phenomena that systematically violated the normative principles of economic theory. In the 1990s, emotions were shown to play a significant role in various forms of decision-making, in particular concerning decisions that involved a high level of risk and uncertainty [40, 58–60].
According to Epstein and Pacini [61], people understand reality through two interactive, parallel processing systems. The rational system is a deliberative, analytical system that functions using established rules of logic and evidence (such as the prospect theory). This system makes it possible for individuals to consciously seek knowledge, develop ideas, and analyze. On the other hand, the experiential, emotional system codes reality in images, metaphors, and narratives to which affective feelings are attached. This system enables individuals to learn from experience without consciously paying attention. Individuals differ in the extent to which the rational and experiential systems influence their decision-making. The balance between these two processes is influenced by various factors, such as age and cognitive load, both of which result in a greater dependence on affect. By affect, the “faint whisper of emotion” that influences decisions directly is meant, and is not simply an answer to a prior analytical evaluation [41, 60, 62].
People therefore base their judgment on a certain activity, not just on what they think, but also on what they feel. If they have a good feeling about a certain activity, they assess the risk as low and the benefit as high. However, if they do not have a good feeling, they will judge the risk as high and the benefit as low. This is called “affect heuristic” in the literature. If the consequences are highly affective, as in the case of the lottery or cancer, there is little variation. For example, research by Loewenstein and Prelec [8] showed that people expressed the same feelings regarding winning the lottery whether the chance was 1 in 10 million or 1 in 10 000 [41, 59, 60].
In any case, it is clear that emotions, which can be interpreted and expressed as moral principles, should be much more considered in risk indexing and risk calculations than is the case today. Section 4.10.4 therefore suggests an approach to calculate risks, where both rational and moral factors are taken into account.
4.1.8 Influence of Regret and Disappointment on Decision-making
People always wish that they had made a different decision if the decision they made turns out to have negative consequences. This feeling is even stronger if it turns out that the alternative would have resulted in a more favorable outcome. In such situations, people experience a feeling of regret. Regret is a psychological response to the making of a wrong decision. A “wrong” decision is defined based on the actual outcome and not on the information available at the moment the decision was made. Regret can result from comparison of an outcome with an outcome that would have resulted from making a different decision. Regret therefore has much in common with opportunity cost (see Chapter 5).
Regret can affect people in two ways. First of all, it can lead people to try to undo the consequences of their regretted choice after the decision has been made. Second, if they anticipate the regret they would later feel, it can influence the choice they make before the decision is taken. A new decision-making model was developed based on this anticipatory aspect of regret – the “regret theory.” Whereas classical theories assume that the expected utility of a choice depends only on the possible pain or pleasure associated with the outcome of that choice, in regret theory utility also depends on the feelings caused by the outcome of the rejected choices. Regret theory is based on two fundamental assumptions. The first is that people compare the real outcome with the outcome that would have resulted from making a different choice. As result of this, people experience certain feelings: regret, if the choice that they did not make would have resulted in a more favorable outcome; and pleasure, if the choice made has produced the best possible outcome. The second assumption of the regret theory is that the emotional consequences of the decision are anticipated and taken into account when making that decision. Different experiments have shown that such behavior results in a more risk-averse attitude. However, this is not always the case. Although most people do their best to avoid regret, this does not only result in more risk-averse behavior, but can also lead people to display more risk-seeking behavior. An aversion to regret can therefore result in choosing an outcome with the lowest (negative) risk as well as in choosing an outcome with the highest (negative) risk. Experiencing regret and disappointment also has another consequence, which is that avoiding feedback so as not to experience regret and disappointment means that people do not learn from their experiences [3, 13, 59, 63].
As well as regret and pleasure, people can also experience disappointment when making a choice between alternatives. Disappointment is a psychological response to an outcome that does not correspond to expectations. When people make a decision, they can experience these feelings when comparing uncertain alternatives. However, it is not always possible to compare the outcome of a chosen alternative and the outcome of an alternative that was not chosen. Imagine that a choice needs to be made between a certain alternative and an uncertain one. If an alternative is chosen with outcome characteristics with some probability, it is always clear what the result of the other (certain) alternative would be. However, if the certain alternative is chosen, it is not always possible to determine whether this choice resulted in a more favorable outcome or not, because one does not know whether the uncertain alternative would have been realized or not [3, 13, 59, 63].
It is possible to translate the principle of regret theory into industrial practice by using expected hypothetical benefits (see also Section 4.2.4) to aid decision-making. To this end, later in this book, expected hypothetical benefits are explained in greater depth and they are used in cost-benefit analysis (see Chapter 5) and cost-effectiveness analysis (see Chapter 6) approaches for decision-making purposes.
4.1.9 Impact of Intuition on Decision-making
The accuracy of decision-making is often inversely proportional to the speed with which decisions need to be made. To explain the fact that people are able to make high-quality decisions relatively quickly, most researchers focus on intuition. Individuals mainly make use of intuition when they are faced with severe time constraints. After all, intuition is based on our innate ability to synthesize information rapidly and effectively and could therefore be essential in successfully solving complex tasks in a short space of time. However, intuitively making decisions does not always result in accurate decisions, as applying intuition only results in speed, sometimes at the expense of accuracy [62, 64].
4.1.10 Other Influences while Making Decisions
In addition to emotions, there are also other factors that influence decision-making. The knowledge available within the decision context also determines an individual's behavior when choosing between alternatives. Research shows that individuals who are not experts are typically overconfident. They overestimate the quality of their abilities and knowledge and perceive extreme probabilities as not so extreme. Experts and more qualified people, on the other hand, are more sensitive to the risk associated with a hypothetical gamble and display more risk-averse behavior, as shown in the research of Donkers et al. [65]. Second, age also has an impact on the decision-making process. The older an individual, the more experience they have and the more capable they are of curtailing overconfidence and therefore responding like an expert. Older people have a more accurate idea of their knowledge and the limits of that knowledge [66, 67].
Finally, gender also plays a large role in decision-making. Many studies have highlighted the fact that men are more risk-seeking than women. The reasons for this difference in approach to risk have already been investigated in various research areas. They can be caused by nature or nurture, or a combination of the two. For example, (young) boys are expected to take risks when participating in competitive sports, whereas (young) girls are often encouraged to be careful. The high-risk choices that men make may therefore be the result of the way in which they were raised by their parents. The same applies to women's risk aversion. Another possible explanation for gender differences is that the way in which risk is experienced relates to the cognitive and non-cognitive differences between men and women. It should be pointed out that women who acquire more competences, become more confident or obtain more knowledge show increased risk-seeking behavior when making decisions. However, such factors have an opposite effect on men, who display more risk-averse behavior with increasing expertise and confidence. Finally, the framing of a decision problem strongly influences the way in which a man makes a decision, but not a woman [14, 66, 68, 69].
4.2 Making Decisions to Deal with Operational Safety
4.2.1 Introduction
In the previous section, the way in which people make decisions and choices, and all the accompanying influencing psychological principles, was discussed. It is obvious that decision theory and making choices under uncertainty are not at all easy to model. The very nature of operational safety management, safety being defined as “a dynamic non-event,” makes it very hard to develop a decision-supporting model. Nonetheless, safety managers need to make such decisions, based on their emotions, their intuition, and the available information and its accompanying uncertainty and/or variability. Making decisions to deal with operational safety should be as accurate as feasible, rational, cost-effective, simple yet not over-simplified, no-nonsense and pragmatic, and, most importantly, as effective as possible (so that there are as many non-events as possible). To this end, a number of possible decision-making approaches may be worked out and will be elaborated upon and explained in the remainder of this book. The decision process should lead to adequate and optimized (according to the company's safety management characteristics) risk treatment. The concept of “risk treatment” should be explained at this point. There are several possible ways to treat risks:
- 1. Risk treatment option 1: risk reduction
- a. Risk avoidance
- b. Risk control.
- 2. Risk treatment option 2: risk acceptance
- a. Risk retention
- b. Risk transfer.
Organizations basically have two main options to deal with risks: they can either accept the risks, or they can reduce the risks. Risk reduction options involve technological, organizational/procedural, and human factor prevention and mitigation measures in order to decrease the risk level. Risk acceptance options, on the other hand, encompass measures that reduce the financial impact of the risks on the organization. There are two sub-options available within each of the two main options [70]. For risk reduction these are risk avoidance and risk control, whereas for risk acceptance, these are risk retention and risk transfer.
4.2.2 Risk Treatment Option 1: Risk Reduction
Risk avoidance and risk control can be achieved in an optimal way by inherent safety or design-based safety. There are five principles of design-based safety. The possible implementation of these five principles is explained for the case of the chemical industry, illustrated in Figure 4.4.

Figure 4.4 Five principles of design-based safety implemented in the chemical industry.
(Source: Kletz [71, 72]. Reproduced with permission from Taylor & Francis.)
As explained by Meyer and Reniers [73], techniques of risk reduction aim to minimize the likelihood of occurrence of an unwanted event and/or the severity of potential losses as a result of the event, or aim to make the likelihood or outcome more predictable. They are applied to existing processes and situations and can be listed as:
- Substitution – by replacing substances and procedures by less hazardous ones, by improving construction work, and so on. Care should be taken that there is not simply a replacement of risk.
- Elimination of risk exposure – this consists in not creating or completely eliminating the condition that could give rise to the exposure to risk.
- Prevention – combines techniques to reduce the likelihood/frequency of potential losses.
- Protection/mitigation – these are techniques whose goal is to reduce the severity of accidental losses before/after an accident occurs.
- Segregation – summarizes the techniques used to minimize the overlapping of losses from a single event. This possibility may imply very high costs:
- Segregation by separation of high-risk units
- Segregation by duplication of high-risk units.
Using principles such as elimination, substitution, moderation, and attenuation in the design phase is always better than to use them in an existing situation/process. In the former case, the approach is called design-based safety (as already explained), and in the latter case it is called “add-on safety.” Design-based safety is known to be much more cost-effective than add-on safety, certainly in the long term. Hence, from an economic viewpoint, design-based safety should always be preferred.
4.2.3 Risk Treatment Option 2: Risk Acceptance
Risk retention and risk transfer, both sub-options of risk acceptance, only differ in the financial consequences of a risk turning into an accident. Risk retention concerns intentionally or unintentionally retaining the responsibility for a specified risk. Intentional retention is referred to as “risk retention with knowledge” and can be seen as a manner of self-insurance or auto-financing, finance planning of potential losses by an organization's own resources. Unintentional retention is referred to as “risk retention without knowledge,” which is caused by inadequate hazard identification and insufficient risk assessment and management.
Usually, self-insurance will only be an option for large organizations able to set up and administrate an insurance fund. It is important to understand that only those losses that are predictable through statistical calculations, thus mainly type I risks, should be retained within an organization. Companies should avoid those risks (of mainly type II), possibly resulting in a major catastrophe or bankruptcy. The advantage of self-insurance is that insurance premiums should be lower, as there are no intermediaries expecting payments for costs, profits, or commissions. In such cases, the insured party also receives the benefit of investment income from the insurance fund that has been established, and keeps any profit accrued from it. Hence, there is an incentive for an organization to practice good risk management principles. However, there is also a downside to auto-financing: a self-insured organization will usually establish its insurance fund based on a statistical normal distribution of losses, being calculated over an extended time period. Hence, as company losses for some insurable type II risks may occur within 20 years but also the next day, there may be insufficient funds accrued to cope with certain losses, especially during the early years of the insurance fund.
Risk transfer involves shifting the responsibility for a specified risk to a third party. Insurance represents an important option for an organization to deal with risks. Risks can – in total or in part – be transferred to external agents, and hence the organization may carry out its business with the reassurance that if an accident occurs that is insured, the insurance company will provide an indemnity.
As risk transfer provides little incentive for a company to significantly reduce risk levels, there used to be a time when “risk management” was considered by company management as “insurance management.” This period is rightfully a long time ago. Companies nowadays realize that not all risks are insurable, and that for those risks that are insured, there are often large uninsured consequences, besides those that are insured and that will be compensated. Risks that are typically covered by insurance include employer's liability, public liability, product liability, fire, and transport. Uninsured risks typically include equipment repairs, employee sick pay, loss of production, staff replacement, damage to corporate image, and accident investigations. A more elaborated list of incident and accident costs is given in Section 4.3 and also further in Chapter 5 on cost-benefit analysis.
4.2.4 Risk Treatment
Risk treatment is the selection and implementation of appropriate options for dealing with risk. It includes choosing among risk avoidance, risk reduction, risk transfer, and/or risk retention, or a combination thereof. Often, there will be residual risk which cannot be removed totally as it is not cost-effective to do so. Risk treatment thus involves identifying the range of options for treating risks, assessing these options financially and preparing and implementing treatment plans. The risk management treatment measures may be summarized as:
- avoid the risk – decide not to proceed with the activity likely to generate risk;
- reduce the likelihood of harmful consequences occurring;
- reduce the consequences occurring;
- transfer the risk – cause another party to share or bear the risk;
- retain the risk – accept the risk and be prepared if an accident occurs.
Risk treatment should be looked at from an economic viewpoint. Financial aspects can play a pivotal role in advocacy and decision-making on risk treatment by demonstrating the financial and economic value of the different treatment options.
Some new concepts need to be defined to be able to develop an approach to decide between different risk treatment options, i.e., the concepts of variability, normalized variability, and hypothetical benefit.
Variability can be defined as the maximum variation between the possible costs of every risk treatment option. Variability can thus be calculated as the difference between the maximum cost and the minimum cost of risk treatment, and doing this for every risk treatment option. As the possible costs per risk treatment option really are different depending on the scenario, variability does not depend on the measurement process used to estimate the costs.
The following formula can be used to determine the variability:
The normalized variability can then be determined by:
The hypothetical benefit of the risk treatment option can be defined in two ways:
- Definition (i) – as the difference between the highest possible costs of an accident in the current situation and those of an accident after applying the treatment measure; hence:

- Definition (ii) – as the difference between the costs of retention when doing nothing (taking no action) and those of the possible accident after applying the treatment measure; hence:

Based on the risk attitude of the decision-maker, one of both hypothetical benefit definitions may be preferred and chosen.
Notice that uncertainty is not the same as variability (as previously explained in this book). Uncertainty is the result of not having sufficient information. It can be considered the result of not being able to measure with sufficient precision, and hence, simply put, it is the result of imprecise methods of measurement [74]. As all measurement methods are imprecise, at least to some degree, all information is accompanied by a high or a low amount of uncertainty. This is the basis of the notion of “risk” and leads to the knowledge that every aspect of decision-making in life is accompanied by risk (see also Chapter 1). It also leads to the distinction between the two types of risk: risks with a lot of information available and hence a low amount of uncertainty (so-called type I risks), and risks with a paucity of information and thus a high amount of uncertainty (so-called type II risks). Risk treatment calculations such as those suggested and illustrated in this section should only be carried out if adequate financial information is available. This relates to type I risks and the more common type II risks.
In the case of definition (i), calculation of the Maxmax hypothetical benefits, emphasis is placed on the consequences of an event, irrespective of the probabilities. In the case of definition (ii), calculation of the expected hypothetical benefits, probabilities are considered. Therefore, definition (i) may be interesting for decision-makers putting more emphasis on consequences (or in case there is a lack of probability information, such as with some type II risks), while definition (ii) would probably be more interesting for decision-makers taking consequences as well as probabilities into consideration (and disposing over the probability information).
It should be noted by the reader that, besides the choice of the definition to determine the hypothetical benefits, which can be rather subjective, the risk treatment calculations approach explained in this section is highly rational and only financial considerations are used to make the calculations and recommendations. No moral aspects, such as equity, justification of the risk, and other ethical aspects, are taken into account in this approach. Therefore, if used, it should be applied with this knowledge in mind. Ethical aspects will be discussed later in this chapter.
4.2.5 The “Human Aspect” of Making a Choice between Risk Treatment Alternatives
Different factors play a role when taking decisions and making choices between various alternatives. The decision-making process becomes even more complicated in an organizational context. Managers need to make decisions concerning issues that affect not only their personal lives, but also the company they work for, its employees, its surroundings, and more. The majority of management problems of any enterprise, including safety investment portfolio management, is characterized by uncertainties and lack of necessary information. The difficulty in predicting future parameter values and future events has an impact on the evaluation of safety investment projects. Uncertainty, or the lack of information, thus obviously hampers managerial decisions. To decrease the level of uncertainty, managers may use historic data, trends, statistical information, qualitative expert judgments, past achievements, and all other information available to the company [37, 75].
Managerial behavior and decision-making sometimes have little affinity with real skills and available resources. The way people think and people behave is much more linked to situational perception and the ability to control processes and potential results. Managers may make different decisions in a similar situation as a result of a different interpretation and evaluation of the situation at hand. Decisions can be divided into two groups: opportunities and threats. Managers usually view controllable situations as opportunities and uncontrollable ones as threats. However, what is interpreted as “controllable” and as “uncontrollable” depends entirely on the person, and varies strongly from manager to manager. Therefore, it is possible that one manager sees a situation characterized by a certain level of uncertainty as an opportunity, while another manager sees the same situation as a threat [75–77].
4.2.5.1 Safety Increase Premium
Preferences toward safety can be described (as already indicated in Chapter 3), by a safety utility function and provide, for example, an idea of the safety state difference one is willing to suffer to leave the person indifferent between an uncertain (but higher) safety state (point B in Figure 4.6) and a certain (but lower) safety state (point A in Figure 4.6). “Uncertain” in this regard indicates that management feels less certain about the effectiveness of the higher safety situation than that of the lower safety situation, and asks, “Is it worth the trouble or money?”

Figure 4.6 Safety increase premium determination.
The safety increase premium can then be calculated as the extra budget that is required to cover the difference between safety state x** and x*, because a certain safety situation x* delivers the same expected utility as the uncertain safety situation x** and its corresponding expected value. Hence, the safety premium can be regarded as the amount of money that safety management needs to invest to get into a higher safety situation (but one perceived as more uncertain with respect to its effectiveness). It is the minimum amount that risk-averse management (cf. the shape of the safety utility function) would need to spend on safety to leave it indifferent between the uncertain and the certain safety situations.
4.3 Safety Investment Decision-making – a Question of Costs and Benefits
4.3.1 Costs and Hypothetical Benefits
Accidents do bear a cost – and often not a small one. An accident can be linked to a variety of direct and indirect costs. Table 4.1 gives a non-exhaustive list of potential costs that might accompany accidents.
Table 4.1 Non-exhaustive list of quantifiable and non-quantifiable socioeconomic consequences of accidents
| Interested parties | Non-quantifiable consequences of accidents | Quantifiable consequences of accidents |
| Victim(s) | Pain and suffering | Loss of salary and bonuses |
| Moral and psychic suffering | Limitation of professional skills | |
| Loss of physical functioning | Time loss (medical treatment) | |
| Loss of quality of life | Financial loss | |
| Health and domestic problems | Extra costs | |
| Reduced desire to work | ||
| Anxiety | ||
| Stress | ||
| Colleagues | Bad feeling | Time loss |
| Anxiety or panic attacks | Potential loss of bonuses | |
| Reduced desire to work | Heavier workload | |
| Anxiety | Training and guidance of temporary employees | |
| Stress | ||
| Organization | Deterioration of social climate | Internal investigation |
| Poor image, bad reputation | Transport costs | |
| Medical costs | ||
| Lost time (informing authorities, insurance company, etc.) | ||
| Damage to property and material | ||
| Reduction in productivity | ||
| Reduction in quality | ||
| Personnel replacement | ||
| New training for staff | ||
| Technical interference | ||
| Organizational costs | ||
| Higher production costs | ||
| Higher insurance premiums | ||
| Administrative costs | ||
| Sanctions imposed by parent company | ||
| Sanctions imposed by the government | ||
| Modernization costs (ventilation, lighting, etc.) after inspection | ||
| New accident indirectly caused by accident (due to personnel being tired, inattentive, etc.) | ||
| Loss of certification | ||
| Loss of customers or suppliers as a direct consequence of the accident | ||
| Variety of administrative costs | ||
| Loss of bonuses | ||
| Loss of interest on lost cash/profits | ||
| Loss of shareholder value |
Meyer and Reniers [73]. Reproduced with permission from De Gruyter.
Hence, by implementing a sound safety policy and by adequately applying operational risk management, substantial costs can be avoided, namely all costs related to accidents that have never occurred (i.e., the non-events), the so-called “hypothetical benefits.” However, in current practice, companies place little or no importance on the “hypothetical benefit” concept due to its complexity. In Section 4.2.4 an attempt has been made to make the concept more tangible. In Section 8.12 the concept is explored even more in depth, as hypothetical benefits are equated and modeled as a maximum investment willingness.
Non-quantifiable costs are highly dependent on non-generic data such as individuals' characteristics, a company's culture and/or the company as a whole and even socio-economic circumstances. Rather, the costs assert themselves when the actual costs supersede the quantifiable costs. In economics (e.g., in environment-related predicaments) monetary evaluation techniques are often used to specify non-quantifiable costs, among them the contingent valuation method and the conjoint analysis or hedonic methods. In the case of non-quantifiable accident costs, various studies have demonstrated that these form a multiple of the quantifiable costs [73].
The quantifiable socioeconomic accident costs (see Table 4.1) can be divided into direct and indirect costs. Direct costs are visible and obvious, while indirect costs are hidden and not immediately evident. In a situation where no accidents occur, the direct costs result in direct hypothetical benefits, whilst the indirect costs result in indirect hypothetical benefits. The resulting indirect hypothetical benefits comprise, for example, not having sick leave or absence from work, not having staff reductions, not experiencing labor inefficiency and not experiencing change in the working environment. Figure 4.7 illustrates this reasoning.

Figure 4.7 Analogy between total accident costs and hypothetical benefits.
(Source: Meyer and Reniers [73]. Reproduced with permission from De Gruyter.)
Although hypothetical benefits seem to be rather theoretical and conceptual, they are nonetheless important if you are to fully understand safety economics. Hypothetical benefits resulting from non-occurring accidents or “non-events” can be divided into different categories at the organizational level, depending on the preferences and characteristics of the organization and its safety management. Meyer and Reniers [73], for example, mention five classes of hypothetical benefits. The first category concerns the non-loss of work time and includes the non-payment of the employee who at the time of the accident adds no further value to the company (if payment were to continue, this would be a pure cost). The non-loss of short-term assets forms the second category and can include, for example, the non-loss of raw materials. The third category involves long-term assets, such as the non-loss of machines. Various short-term benefits, such as non-transportation costs and non-fines, constitute the fourth category. The fifth category consists of non-loss of income, non-signature of contracts or non-price reductions. In Chapter 5, hypothetical benefits are elaborated in greater depth. Independent of the number of classes or categories used, the visible or direct hypothetical benefits generated by the avoidance of costs resulting from non-occurring accidents only make up a small portion of the factors responsible for the total hypothetical benefits resulting from non-occurring accidents.
Next to tangible benefits, intangible benefits might exist. Intangible benefits may manifest themselves in different ways, e.g., non-deterioration of image, avoidance of lawsuits, and the fact that an employee, thanks to the safety policy and the non-occurrence of accidents, does not leave the organization. If an employee does not leave the organization, the most significant benefit arises from work hours that other employees do not have to make up. Management time is consequently not given over to interviews and routines surrounding the termination of a contract. The costs of recruiting new employees can, for example, prove considerable if the company has to replace employees with experience and company-specific skills. Research into the reasons that form the basis of recruitment of new staff reveals a difference between, on the one hand, the recruitment of new employees due to the expansion of a company and, on the other hand, the replacement of staff who have resigned due to poor safety policies.
4.3.2 Prevention Benefits
An accident that does not occur in an enterprise, thanks to the existence of an efficient safety and prevention policy within the company, was referred to as a non-occurring accident or a non-event. Non-occurring accidents (in other words, the prevention of accidents) result in the avoidance of a number of costs and thus create hypothetical benefits, as explained previously. An estimation of the amount of input and output of the implementation of a safety policy is thus clearly anything but simple. It is impossible to specify the costs and benefits of one exceptional measure. The effectiveness (and the costs and benefits) of a safety policy must be regarded as a whole.
Hence, if an organization is interested in knowing the efficiency and the effectiveness of its safety policy and its prevention investments, in addition to identifying all kinds of prevention costs, it is also worth calculating the hypothetical benefits that result from non-occurring accidents. By taking all prevention costs and all hypothetical benefits into account, the true prevention benefits can be determined.
4.3.3 Prevention Costs
In order to obtain an overview of the various kinds of prevention costs, it is appropriate to distinguish between fixed and variable prevention costs, on the one hand, and direct and indirect prevention costs on the other.
Fixed prevention costs remain constant irrespective of changes in a company's activities. One example of a fixed cost is the purchase of a fireproof door. This is a one-off purchase and the related costs are not subject to variation in accordance with production. Variable costs, in contrast to fixed costs, vary proportionally in accordance with a company's activities. The purchase of safety gloves can be regarded as a variable cost due to the fact that the gloves have to be replaced sooner when used more frequently or more intensively due to increased productivity levels.
Variable prevention costs have a direct link with production levels. Fixed prevention costs, by contrast, are not directly linked to production levels. A safety report, for example, will state where hazardous materials must be stored, but this will not have a direct effect on production. The development of company safety policy includes not only direct prevention costs, such as the application and implementation of safety material, but also indirect prevention costs such as development and training of employees and maintenance of the company safety management system.
A non-exhaustive list of prevention costs is as follows:
- staffing costs of company HSE department;
- staffing costs for the rest of the personnel (time needed to implement safety measures, time required to read working procedures and safety procedures, etc.);
- procurement and maintenance costs of safety equipment (e.g., fire hoses, fire extinguishers, emergency lighting, cardiac defibrillators, pharmacy equipment);
- costs related to training and education with respect to working safely;
- costs related to preventive audits and inspections;
- costs related to exercises, drills, simulations with respect to safety (e.g., evacuation exercises, etc.);
- a variety of administrative costs;
- prevention-related costs for early replacements of installation parts, and so on;
- maintenance of machine park, tools, and so on;
- good housekeeping;
- investigation of near-misses and incidents.
In contrast to quantifying hypothetical benefits, companies are usually very experienced in calculating direct and indirect (non-hypothetical) costs of preventive measures.
4.4 The Degree of Safety and the Minimum Overall Cost Point
As Fuller and Vassie [70] indicate, the overall (or total) cost of a company safety policy will be directly related to an organization's standards for health and safety, and thus its degree of safety. The higher the company's health and safety standards and its degree of safety, the greater the prevention costs, and the lower the accident costs within the company. Prevention costs will rise exponentially as the degree of safety increases, because of the law of diminishing returns, which describes the difficulties of trying to achieve the last small improvements in performance. If a company has already made huge prevention investments, and the company is thus performing very well on health and safety, it becomes ever more difficult to further improve its health and safety performance with one extra “unit” (in economics also called “marginal” improvement). On the contrary, the accident costs will decrease exponentially as the degree of safety improves because, as the accident rate is reduced, and hence accident costs are decreased, there is ever less potential for further (accident reduction) improvements (see Figure 4.8).

Figure 4.8 Prevention costs and accident costs as a function of the degree of safety (qualitative figure).
From a purely microeconomic viewpoint, a cost-effective company will choose to establish a degree of safety that allows it to operate at the minimum total cost point. Figure 4.8 illustrates this reasoning. At this point, the prevention costs are balanced by the accident costs, and at first sight the “optimal safety policy” (from a microeconomic point of view) is realized. It is important that for this exercise to deliver results that are as accurate as possible, the calculation of both prevention costs and accident costs should be as complete as possible, and all direct and indirect, visible and invisible, costs should be taken into account. However, Figure 4.8 indicates that, in an optimal cost-effective situation, one should not strive for a zero-accident situation. But is this really always the case? As will be explained further, this is possibly not always the case.
As it happens, an observation is that companies who have aspired to zero accidents globally over very long periods are still in business, and indeed even highly profitable. Their safety and profitability records are usually better than those with fatalistic beliefs that some accidents are inevitable and that they should/can be considered part of the cost-effectiveness policy of the company. Figure 4.8 was actually first produced in the quality management context and originally looked like Figure 4.9. Despite the reasoning that an optimum overall cost point is not at zero accident level, many manufacturers that did aim for zero quality defects (no matter the theory) largely achieved their aims, despite what is shown in Figure 4.9.

Figure 4.9 Conventional cost-benefit analysis for determining the tolerable accident level in quality management.
Panopoulos and Booth [78] sought to challenge the conclusions drawn from Figure 4.9, namely that zero accidents could “never” be the optimum outcome. To this end, they assumed that the starting point of prevention costs for a safety minimum overall cost graph needs to be zero accidents, achieved at finite cost, not infinite cost (as this must also be true in real industrial practice). From that initiating point, the trends in accident and prevention costs as accident numbers increase may be explored. It should be noted that the novel presentation method is not profound. Its key purpose is to challenge the existing ideas regarding the minimum overall cost curve (cf. Booth [79]).
Figures 4.10 and 4.11 present graphical minimum overall cost curves, assuming finite values of prevention costs for zero accidents.

Figure 4.10 Conventional cost-benefit analysis (Figure 4.9 redrawn) showing zero accidents as not the optimum case.

Figure 4.11 Conventional cost-benefit analysis showing zero accidents as the optimum case.
Figure 4.11 shows the case where zero accidents offer the cheapest option. Everything turns on the relationship between accident and preventive costs as the number of accidents goes up, and where the minimum overall cost lies.
What, then, are the factors that determine whether Figure 4.10 or 4.11 applies? Figure 4.10 is identical to Figure 4.9 but drawn in a different way, as in the latter the cost of each accident is relatively modest, and prevention costs rise dramatically as zero is approached. This might typically be where safety expenditure is not cost-effective. In contrast, Figure 4.11 shows zero accidents as the optimum case. Here each accident is more expensive than shown in Figure 4.10, and the costs of moving from a small number of accidents to zero are relatively modest. A question that arises is: what are the practical circumstances where zero accidents is the minimum cost option?
As Booth [79] explains, the arguments for zero quality defects provides the clue, but also the challenge. Frequent, albeit minor, quality defects threaten sales (and product safety, where the effects can be catastrophic). Moreover, quality management was revolutionized when the change was made from rectifying defects “at the end of the production line” to the more cost-effective approach of quality checks being incorporated into every task – so achieving zero defects at the end of the line via a dramatically better preventive approach. Returning to accidents, zero accidents are more likely to offer the best business case where the costs of an accident are high, as with type II events. Hence, Figure 4.11 provides a good argument for zero type II events or zero major accidents, while the pursuit of zero type I events or zero occupational accidents should be treated like Figure 4.10. In summary, using a cost-benefit analysis to determine a minimum overall cost is only suitable for one type of risk (type I risks) and not for other risks (type II). But the cost-benefit exercise results will still be largely improvable, and the next paragraph and section explain why and how.
Earlier in this section, the phrase “from a microeconomic point of view” was mentioned, due to the fact that victim costs and societal costs should, in principle, also be taken into account in the overall/total costs calculations. If only microeconomic factors are important for an organization, only accident costs related to the organization are considered by the company, and not the victim and societal costs. Hence, even if all direct and indirect accident costs are determined by an organization, there will be an underestimation of the full economic costs, due to individual and macroeconomic costs. True accident costs are composed of the organizational costs, as well as the costs to the victim and to society.
Organizations should thus make a distinction between the different types of risk, and between real accident costs and hypothetical benefits. Costs of accidents that happened (“accident costs”) and costs of accidents that were avoided and never happened (“hypothetical benefits” due to non-events) are completely different in nature: many more non-events happen than accidents. Nonetheless, their analogy is clear and therefore they are easily confused when making safety cost-benefit considerations. Curves such as those in Figure 4.8 are only valid for type I risks, as the curve of “accident costs” (displaying the costs related to a certain degree of safety) can only be empirically determined if a large number of accidents happened, and thus if sufficient data are available. It is impossible to determine empirically the costs of disasters linked to a certain degree of safety, simply because not that many catastrophes happen, which would be necessary to obtain sufficient information to draw such a curve. Hence, the curves displayed in Figure 4.8 cannot be drawn – and should not be used – for type II risks. At best, a thought experiment can be conducted, with a resulting Figure 4.11 being applicable to type II events.
4.5 The Type I and Type II Accident Pyramids
Heinrich [80], Bird [81], and James and Fullman [82], among other researchers, mentioned the existence of a ratio relationship between the numbers of incidents with no visible injury or damage, and those with property damage, those with minor injuries, and those with major injuries. This accident ratio relationship is known as “the accident pyramid” or “the safety triangle.” Figure 4.12 illustrates such an accident pyramid (or safety triangle). Accident pyramids unambiguously indicate that accidents with higher consequences are “announced” by accidents with lesser consequences. Hence the importance of, among other things, awareness and incident analyses for safety managers.

Figure 4.12 The Bird accident pyramid (“Egyptian”).
Studies [80–82] found different ratios (varying from 1 : 300 to 1 : 600), depending on the industrial sector, the area of research, cultural aspects, and so on. Although the statistical relationship between the different levels of the pyramid has never been proven, the existence of the accident pyramid obviously has merits from a qualitative point of view. From a qualitative interpretation of the pyramid, it could be possible to prevent serious accidents by taking preventive measures aimed at near misses, minor accidents, and so on. Hence, these “classic” accident pyramids clearly provide an insight into type I accidents, where a lot of data are at hand. In brief, the assumptions of the “old” safety paradigm emanating from the accident pyramid (see Figure 4.12) hold that:
- 1. As injuries increase in severity, their number decreases in frequency.
- 2. All injuries of low severity have the same potential for serious injury.
- 3. Injuries of differing severity have the same underlying causes.
- 4. One injury reduction strategy will reach all kinds of injuries equally (i.e., reducing minor injuries by 20% will also reduce major injuries by 20%).
Using injury statistics, Krause [83] indicated that while minor injuries may decline in companies, serious injuries can remain the same, hence casting credible doubts on the validity of the safety pyramid concept. In fact, research indicated that only some 20% (21% to be precise) of the type I incidents have the potential to lead to a serious type I accident. This finding implies that if one focuses only on “the other 80%” of the type I incidents (i.e., the 80% of the incidents that are unlikely to lead to serious injury), the causative factors that create potential serious accidents will continue to exist and so will the serious accidents themselves.
Therefore, Krause [83] proposed a “new” safety paradigm with the following assumptions:
- 1. All minor injuries are not the same in their potential for serious injury or fatality. A subset of low severity injuries come from exposures that act as a precursor to serious accidents.
- 2. Injuries of differing severity have differing underlying causes.
- 3. Reducing serious injuries requires a different strategy than reducing less serious injuries.
- 4. The strategy for reducing serious injuries should use precursor data derived from accidents, injuries, near misses, and exposure.
Based on research by Krause [83] on the different types of uncertainties/risks available, and on several disasters (such as the BP Texas City Refinery disaster of 2005), the classic pyramid shape thus needed to be refined and improved. Instead of an “Egyptian” pyramid shape, such as the classic accident pyramid studies suggest, the shape should rather be a “Mayan” one, as illustrated in Figure 4.13.

Figure 4.13 Mayan accident pyramid shape.
(Source: Meyer and Reniers [73]. Reproduced with permission from De Gruyter.)
First, only 20% of the near misses at the bottom of the pyramid have the potential to become serious accidents. This is indicated by the hatched part of the light gray zone in Figure 4.13. Second, the shape of the pyramid should be Mayan instead of Egyptian. The Mayan pyramid shape shows that there is a difference between type I and type II risks; in other words, “regular accidents” or occupational accidents (and the incidents going hand-in-hand with them) should not be confused with “major accidents” or catastrophes. Not all near misses have the potential to lead to disaster, but only a minority of unwanted events may actually end up in a catastrophe. Obviously, to prevent disasters and catastrophes, risk management should be aimed at both types of risk, and certainly not only at the large majority of “regular” risks. Hopkins [84] illustrates this by using a bi-pyramid model, consisting of two pyramids partially overlapping. One pyramid represents type I risks, leading at most to a serious accident (e.g., a lethality), but not to a true catastrophe, and the other pyramid represents type II risks, with the potential to lead to a disaster. The overlap is present (and also in the Mayan pyramid of Figure 4.13 represented by the dark gray areas) because in some cases, unwanted events may be considered as warnings or incidents for both pyramids. Hopkins [84] indicates that the airline industry was the pioneer for this kind of type I and type II risk thinking. In that industry, taking all necessary precautionary measures to ensure flight safety is regarded as fundamentally different from taking preventative measures to guarantee employee safety and health. Two databases are maintained by airline companies: one is used to keep data of near-miss incidents affecting flight safety and the other stores information regarding workforce health and safety. Hence, in this particular industry, it is clear that workforce injury statistics say nothing about the risk of an aircraft crash. This line of type I and type II risk thinking can (and should) be implemented in every industrial sector.
4.6 Quick Calculation of Type I Accident Costs
The Bird pyramid can be used to make a rough estimate of the total yearly costs of occupational accidents within an organization, based on the number of “serious” accidents, where serious accidents are defined as accidents where the victim has at least 1 day off work [so-called lost time injury (LTI) accidents]. If, as the Bird pyramid suggests, different sorts of type I accidents are discerned, different metrics for different kind of accidents are used.
4.6.1 Accident Metrics
For accidents defined as occurrences that result in a fatality, permanent disability or time lost from work of 1 day/shift or more, usually the LTI frequency rate (LTIFR) is used and these accidents are referred to as “LTI accidents.” The LTIFR is the number of lost time injuries per million hours worked, calculated using the following equation:
Hence, the LTIFR is how many LTIs occurred over a specified period per 1 000 000 hours (or some other number; 100 000 is also often used) worked in that period. Mostly, the accounting period is chosen to be 1 year. By counting the number of hours worked, rather than the number of employees, for example, discrepancies in the incidence rate calculation as a result of part-time workers and overtime are avoided. However, this metric using the employees instead of the number of hours worked [called the lost time injury incidence rate (LTIIR)] is also used in many organizations. To calculate the LTIIR, which is the number of LTIs per 100 employees, the following equation is used:
Next, the severity rate, which takes into account the severity per accident, is also often used. Depending on how this is expressed, at least the information from above and the number of work days lost over the year are needed. Often the severity rate is expressed as an average by simply dividing the number of days lost by the number of LTIs. Another way of calculating the LTI severity rate (LTISR) is to use the following equation (the figure 1 000 000 may be replaced by any other figure; it just tells us that the LTISR in this case is expressed per million hours worked):
Also, the medical treatment injury (MTI) frequency rate is often measured. This frequency rate measures how often MTIs are occurring. It is expressed as the number of MTIs per million hours worked:
Finally, the total recordable injury frequency rate (TRIFR) measures the frequency of recordable injuries, i.e. the total number of fatalities, LTIs, MTIs, and restricted work injuries occurring. It is expressed as the total number of fatalities, LTIs, MTIs, and restricted work injuries per million hours worked:

4.6.2 A Quick Cost-estimation Approach for Type I Risks
Companies usually have a good understanding of the cost per sort of type I accident. For example, the average cost of an LTI accident is calculated on a yearly basis by organizations, and equals €x. Similarly, the average costs of the different sorts of accidents can be determined. Figure 4.14 shows some theoretical ways of calculating the different costs.

Figure 4.14 The Bird accident pyramid with costs per type of accident.
(Source: Meyer and Reniers [73]. Reproduced with permission from De Gruyter.)
Based on these average costs, a rough estimate of the total yearly cost due to type I accidents can be made. Every company usually knows very well the number of serious accidents that happen annually, but the numbers of other type I accidents with lesser consequences are often unknown. Nonetheless, a rough estimation of all accident costs can be made using the type I (e.g., Bird) pyramid principle. In principle, an organization should draft its own pyramid, and use these ratios. Assume that the number of serious accidents is N, and hence this rough calculation can be done for any company. Table 4.2 displays how to calculate the total yearly accident costs.
Table 4.2 Quick calculation of the total yearly costs based on the number of “serious” type I accidents
| Sort of incident/accident | Bird pyramid | Number of incidents/accidents | Cost per sort of incident/accident | Cost |
| Serious | 1 | N | x | Nx |
| Minor injury | 10 | 10N | y | 10Ny |
| Property damage | 30 | 30N | z + t | 30N(z + t) |
| Incident | 600 | 600N | s | 600Ns |
| Total cost = N[x + 10y + 30(z + t) + 600s] | ||||
Table 4.2 shows that, based on the ratio between “serious” type I accidents and other sorts of accidents, a rough estimate can be made of the total average accident costs for a given year if the number of incidents and accidents in that year is known, and if the average cost per sort of accident is known. Table 4.2 doesn't take into consideration the fact that only around one-fifth of all accidents lead to serious accidents (see Section 4.5), as this knowledge has no impact on the overall costs of all incidents happening in the organization. It does, however, have an impact on the amount of costs avoided purely related to serious accidents, and this should be taken into account when calculating those avoided costs.
This method can be used by a company to estimate, for example, the accident cost line displayed in Figure 4.8, when calculating the costs for different levels of safety. Clearly, the definition of a “level of safety” would have to be agreed upon within the company, and estimations may then be carried out based on this definition.
4.7 Quick Calculation of Type II Accident Costs
4.7.1 Introduction to a Study on Type II Event Decision-making
It is very difficult, if not impossible, to elaborate on a “quick calculation” tool for estimating type II accident costs. In fact, it could be very dangerous as well. It is possible that company managers might reduce the decision-making about type II accidents to a simple mathematical formula, and such a practice would be irresponsible, unacceptable, and wrong. If there is one thing that history teaches, it is that one should be extremely careful with safety investment decision-making where extremely low-frequency events are involved. Hence, instead of working out a method for the quick calculation of type II accidents, we present the results of a study by Van Nunen et al. [85] on decision-making in the case of type II events. It is more of a “psychological” problem than a rational one: the hypothetical benefits achieved in the case of averting a true type II accident are almost always higher than the safety investment costs (SICs) of successful accident avoidance.
The subject of the study concerned the investigation of the influence of probability change in averting a certain loss due to a major (type II) accident. The question that the respondents needed to answer was basically whether they preferred an investment in safety (prevention measures – representing an uncertain gain) or an investment in production (representing a certain gain), for varying levels of potential losses accompanied by varying probabilities of avoiding these losses. The research thus aimed to discover which parameters of consequence and probability would persuade people that investing in production was worth the major accident risk, and which parameters would make the risk or uncertainty unacceptable, leading them to invest in major accident prevention. Knowledge as to how these decisions are made by people in general is obviously important for the understanding and management of activities involving potential type II events [86].
Concerning the decision-making under risk, as already mentioned, accidents with major consequences are included, as well as a variety of probabilities of occurrence. If both the probability of occurrence and the disaster potential are perceived as high, one would normally reject such risks [87]. The acceptance of accidents with high disaster potential and a low probability of occurrence, so-called HILP accidents (i.e., type II accidents), is far less straightforward [46, 51]. It could be argued that the occurrence of large-scale accidents is unacceptable regardless of their probability. On the other hand, it can be argued that safety has a cost that makes it impossible for organizations to spend an unlimited budget reducing or eliminating all (major) accident scenarios. Therefore, a certain level of risk and uncertainty has to be accepted [88].
In addition to the decision-making under risk (the outcomes as well as the probabilities of each outcome are known), decision-making under uncertainty can also be considered. In an uncertain situation, the probability of an accident occurring is completely unknown and/or the amount of the loss as a result of the accident is also unknown. When these uncertainties remain, subjective judgments are inevitable [87], which makes it difficult to predict the decision-making.
It should be noted that the general results of the choices between the production investment and the prevention investment were compared with the cumulative expected values of these investments. As mentioned at the beginning of this chapter, the theory of expected value can provide a reference for discussing how the decisions are taken [86].
The problem setting is as follows. If a respondent has chosen a production investment, the company will make, during the next 5 years, an extra yearly production profit of €500 000. So, after a 5-year period, the production investment will have resulted in an extra profit of €2 500 000 (interests aside).
The cumulative expected value of the prevention investment depends on the probability that an accident will occur and on the associated amount of losses. The calculation of the cumulative expected value is given for the following example: assume a prevention investment that avoids a major accident with probability of 1 in 100 000 and losses worth €20 000 000 per year during the next 5 years. A probability of 1 in 100 000 corresponds to a probability of 0.001%. This brings the cumulative expected value to (0.001% × 5) × €20 000 000. So, after 5 years, the cumulative expected value will be €1000. The same calculation was carried out for all other combinations of probabilities and losses due to major accidents considered in the questionnaire.
In Table 4.3, the investment (production or prevention) entailing the highest cumulative expected value is given. Based on the answers of the respondents, for each given probability and possible loss, it was calculated whether the largest group of respondents opted for the production or the prevention investment. The distribution of the matrix from the answers of the respondents was then compared with the matrix from Table 4.3.
Table 4.3 Investment with the highest cumulative expected value
| Probability that an accident will occur | |||||
| 1 in 100 000 | 1 in 10 000 | 1 in 100 | 1 in 10 | ||
| Loss of the accident | €20 000 000 | Production | Production | Production | Prevention |
| €50 000 000 | Production | Production | Production = prevention | Prevention | |
| €100 000 000 | Production | Production | Prevention | Prevention | |
| €500 000 000 | Production | Production | Prevention | Prevention | |
| €1 000 000 000 | Production | Production | Prevention | Prevention | |
| €10 000 000 000 | Production | Prevention | Prevention | Prevention | |
As previously stated, several factors can have an influence on the decision-making process. Some factors were thus included in the analyses to determine whether people would decide in a more risk-averse or risk-seeking way. The results were compared according to gender (male or female). Based on the Short Rational-Experiential Inventory, respondents with a high rational thinking style were compared with those with a low rational thinking style, and respondents with a high intuitive thinking style were compared with those with a low intuitive thinking style. Based on the Brief Sensation-Seeking Scale, the choices of the respondents with high sensation-seeking behavior were compared with those with low sensation-seeking behavior.
4.7.2 Results of the Study on Type II Event Decision-making
In Table 4.4, the proportion of respondents opting for the production or prevention investment is given. Table 4.5 shows whether the largest group of respondents opted for the production investment or for the prevention investment. In this table, there is also a comparison between the choices of the respondents and the cumulative expected values of these investments: the distribution of the matrix from the answers of the respondents is compared with the matrix in Table 4.3. For the unknown probabilities of occurrence and the unknown losses of the accident, the cumulative expected value cannot be calculated, which makes this comparison impossible for these investments (in italics in Table 4.5).
Table 4.4 Proportion of respondents who opt for the production or the prevention investment
| Probability that an accident will occur | |||||||
| 1 in 100 000 (%) | 1 in 10 000 (%) | 1 in 100 (%) | 1 in 10 (%) | Unknown (%) | |||
| Loss of the accident | €20 000 000 | Production | 89.4 | 82.2 | 46.7 | 20.0 | 75.9 |
| Prevention | 10.6 | 17.8 | 53.3 | 80.0 | 24.1 | ||
| €50 000 000 | Production | 80.2 | 68.7 | 25.4 | 7.7 | 56.9 | |
| Prevention | 19.8 | 31.3 | 74.6 | 92.3 | 43.1 | ||
| €100 000 000 | Production | 63.2 | 40.2 | 11.1 | 5.4 | 34.0 | |
| Prevention | 36.8 | 59.8 | 88.9 | 94.6 | 66.0 | ||
| €500 000 000 | Production | 30.9 | 19.0 | 4.7 | 2.2 | 16.3 | |
| Prevention | 69.1 | 81.0 | 95.3 | 97.8 | 83.7 | ||
| €1 000 000 000 | Production | 15.1 | 9.7 | 2.0 | 2.0 | 9.2 | |
| Prevention | 84.9 | 90.3 | 98.0 | 98.0 | 90.8 | ||
| €10 000 000 000 | Production | 9.7 | 6.2 | 1.7 | 1.7 | 4.7 | |
| Prevention | 90.3 | 93.8 | 98.3 | 98.3 | 95.3 | ||
| Unknown | Production | 43.2 | 34.2 | 12.0 | 7.2 | 5.0 | |
| Prevention | 56.8 | 65.8 | 88.0 | 92.8 | 95.0 | ||
Table 4.5 Largest group of the respondents who opt for the production or the prevention investment
| Probability that an accident will occur | |||||||
| 1 in 100 000 | 1 in 10 000 | 1 in 100 | 1 in 10 | Unknown | |||
| Loss of the accident | €20 000 000 | Production | Production | Prevention* | Prevention | Production | |
| €50 000 000 | Production | Production | Prevention* | Prevention | Production | ||
| €100 000 000 | Production | Prevention* | Prevention | Prevention | Prevention | ||
| €500 000 000 | Prevention* | Prevention* | Prevention | Prevention | Prevention | ||
| €1 000 000 000 | Prevention* | Prevention* | Prevention | Prevention | Prevention | ||
| €10 000 000 000 | Prevention* | Prevention | Prevention | Prevention | Prevention | ||
| Unknown | Prevention | Prevention | Prevention | Prevention | Prevention | ||
The distribution of the investment of the respondents that does not match the distribution of the investment with the highest cumulative expected value is indicated by an asterisk. In cases where a comparison between the distribution of the investment of the respondents and the distribution of the investment with the highest cumulative expected value is not possible, italics are used.
According to calculated cumulative expected values, the higher the accident probability and the higher the possible loss, the more advantageous it is to choose a prevention investment. If the accident probability is equal to 1 in 100 000, then, according to the theory of expected values, it is always better to opt for the production investment, regardless of the possible loss of the accident (considering the numbers that were used in the survey). The survey results indicate that the respondents make decisions in a more risk-averse way than can be anticipated by the theory of expected values. The majority of the respondents opt for the production investment only when the possible loss of a major accident is equal to €100 000 000 or lower. Regarding the higher probabilities of occurrence, i.e., 1 in 10 000 and 1 in 100, the respondents behave in a more risk-averse way than the cumulative expected values predict. This means that these respondents, being laypeople, also expect company safety managers to be cautious and choose prevention instead of production in such cases. It thus becomes obvious that moral principles should be seen as an important part of decision-making regarding type II risks, in order for them to be acceptable by laypeople. Klinke and Renn [87] explain this risk-averse behavior through the moral obligation that people have to prevent harm to human beings and the environment. They argue that risk refers to the experience of something that people fear or regard as negative. Another explanation can be found in the framework of Random Regret Minimization, which postulates that, when choosing, people anticipate and aim to minimize regret, and therefore behave in a more risk-averse way [89] (see also in the introductory section of this chapter).
As already mentioned, it is extremely difficult to predict decision-making in an uncertain situation where there is no knowledge whatsoever about the probability and/or the losses. It turns out that when there is uncertainty concerning the possible loss of an accident, the majority of respondents opt for the prevention investment, regardless of the probability of the accident occurring. As the accident's probability increases, the number of respondents that choose the production investment decreases. The number of respondents choosing the production investment decreases where the possible losses increase. When there is complete uncertainty, i.e., where both the accident probability and the possible loss are unknown, the majority (95%) opts for the prevention investment. With complete uncertainty, the risk is mostly categorized as intolerable, as the consequences might be catastrophic. Therefore, the risk-averse attitude is perceived as appropriate [87]. Notice that this finding also provides an argument for the precautionary principle.
4.7.3 Results by Gender
Table 4.6 shows the proportion of respondents opting for the production or the prevention investment by gender. When there is a significant difference (P < 0.05) between investments of the male respondents and the female respondents, this is indicated with an asterisk.
Table 4.6 Proportion of respondents who opt for the production or the prevention investment per gender
| Probability that an accident will occur | ||||||||
| 1 in 100 000 (%) | 1 in 10 000 (%) | 1 in 100 (%) | 1 in 10 (%) | Unknown (%) | ||||
| Loss of the accident | €20 000 000 | Production | Male | 88.6 | 82.3 | 48.7 | 17.7 | 80.1 |
| Female | 89.9 | 82.2 | 45.3 | 21.5 | 73.3 | |||
| Prevention | Male | 11.4 | 17.7 | 51.3 | 82.3 | 19.9 | ||
| Female | 10.1 | 17.8 | 54.7 | 78.5 | 26.7 | |||
| €50 000 000 | Production | Male | 84.2 | 68.4 | 25.9 | 5.7 | 52.2 | |
| Female | 77.7 | 69.0 | 25.1 | 8.9 | 59.9 | |||
| Prevention | Male | 15.8 | 31.6 | 74.1 | 94.3 | 47.8 | ||
| Female | 22.3 | 31.0 | 74.9 | 91.1 | 40.1 | |||
| €100 000 000 | Production | Male | 65.2 | 44.9 | 11.4 | 4.4 | 33.8 | |
| Female | 61.9 | 37.2 | 10.9 | 6.1 | 34.1 | |||
| Prevention | Male | 34.8 | 55.1 | 88.6 | 95.6 | 66.2 | ||
| Female | 38.1 | 62.8 | 89.1 | 93.9 | 65.9 | |||
| €500 000 000 | Production | Male | 37.6a | 25.3a | 3.8 | 1.9 | 19.6 | |
| Female | 26.7a | 15.0a | 5.3 | 2.4 | 14.2 | |||
| Prevention | Male | 62.4a | 74.7a | 96.2 | 98.1 | 80.4 | ||
| Female | 73.3a | 85.0a | 94.7 | 97.6 | 85.8 | |||
| €1 000 000 000 | Production | Male | 20.4a | 13.4a | 1.9 | 1.9 | 12.1 | |
| Female | 11.7a | 7.3a | 2.0 | 2.0 | 7.3 | |||
| Prevention | Male | 79.6a | 86.6a | 98.1 | 98.1 | 87.9 | ||
| Female | 88.3a | 92.7a | 98.0 | 98.0 | 92.7 | |||
| €10 000 000 000 | Production | Male | 14.0a | 9.6a | 1.3 | 1.9 | 5.7 | |
| Female | 6.9a | 4.0a | 2.0 | 1.6 | 4.0 | |||
| Prevention | Male | 86.0a | 90.4a | 98.7 | 98.1 | 94.3 | ||
| Female | 93.1a | 96.0a | 98.0 | 98.4 | 96.0 | |||
| Unknown | Production | Male | 45.9 | 37.4 | 11.5 | 5.8 | 5.7 | |
| Female | 41.6 | 32.1 | 12.3 | 8.2 | 4.5 | |||
| Prevention | Male | 54.1 | 62.6 | 88.5 | 94.2 | 94.3 | ||
| Female | 58.4 | 67.9 | 87.7 | 91.8 | 95.5 | |||
a There is a significant difference (P < 0.05) between the investments of the male and female respondents.
There are significant differences between male and female respondents for the lower probabilities of occurrence (1 in 100 000 and 1 in 10 000) in combination with higher possible losses (€500 000 000, €1 000 000 000, and €10 000 000 000). For these combinations, men behave in a more risk-seeking way, i.e., they are more likely to opt for the production investment. When the possible loss increases, this difference between men and women decreases. The results are consistent with existing studies indicating that men behave in a more risk-seeking way than women (e.g., [14, 90, 91]). When it comes to making decisions regarding type II events, men display more risk-seeking decision-making behavior than women. This study also shows that men – regardless of whether they have to take decisions – have higher levels of rational thinking style and sensation-seeking than women, and that women – regardless of whether they have to take decisions – have higher levels of intuitive thinking style (see also the following section).
4.7.4 Rational and Intuitive Thinking Styles
The study revealed that for the combinations of a probability of occurrence of 1 in 10 with possible losses of €20 000 000, €50 000 000, and €100 000 000, the respondents with a high rational thinking style behave in a more risk-averse way than those with a low rational thinking style. For the combination of a probability of occurrence of 1 in 100 000 with an unknown possible loss, respondents with a low intuitive thinking style follow the overall results, i.e., a prevention investment. However, the majority of the respondents with a high intuitive thinking style opted for a production investment for the combination of a probability of occurrence of 1 in 100 000 with an unknown possible loss. These differences are statistically significant. Another significant difference between the high and low intuitive thinking styles is found for the combination of a probability of 1 in 10 000 with an unknown possible loss: respondents with a low intuitive thinking style are more likely to behave in a risk-averse way than respondents with a high intuitive thinking style.
Butler et al. [91] also have done research on how intuition and reasoning or rationality affect the decision-making under risk and uncertainty. They obtained similar results: people with a high intuitive thinking style are more risk-seeking and people with a high rational thinking style are less risk-seeking. Based on the terminology of Stanovich and West [92], individuals with a high rational thinking style rely on effortful, deliberative reasoning and systematic processing of information. On the other hand, when decisions are based on intuition, there is no systematic comparison of alternatives: a decision is taken at glance, by rapidly evaluating the main features of the problem [91]. An explanation for the finding that people with a high intuitive thinking style behave in a more risk-seeking way could be the fact that the high speed of intuitive thinking puts intuitive thinkers at a comparative advantage in situations involving high risk and uncertainty, making them less averse. Intuition can handle severe uncertainty so that individuals who are better at using intuition may feel more comfortable dealing with uncertainty and risk and thus develop higher tolerance for both [91, 93–96]. The downside is that they are only human, and, like anyone, they may become complacent or over-optimistic, which could make them blind for disaster. Hence, the high reliability organization (HRO) principles, as discussed in Chapter 2, should be applied to overcome such a possibility.
For the combination of a probability of 1 in 10 000 and an unknown possible loss, respondents with a high sensation-seeking style make decisions in a more risk-seeking way than respondents with a low sensation-seeking style. As already shown in a number of studies, higher levels of self-reported sensation-seeking are indeed associated with greater risk taking on various domains (e.g., [97–100]).
4.7.5 Conclusions of the Study on Type II Event Decision-making
Decision-making under risk and uncertainty is obviously not straightforward, and the acceptance of risk and uncertainty is influenced by a number of factors. Knowledge of these decision-making processes is important for the understanding and management of activities involving potential major accident events. This study illustrates that people behave in a more risk-averse way as compared with what would be expected based on the theory of expected values, in the case of decision-making involving type II risks. Only for low accident probabilities combined with low potential losses do the respondents take more risk-seeking decisions and opt for production investments. Concerning decision-making under uncertainty, the respondents also make risk-averse decisions: only for known and relatively low possible losses do they opt for the production investment; otherwise they always choose prevention. Under complete uncertainty, almost all respondents behave in a risk-averse manner. The study also showed that men are more likely to behave in a risk-seeking way than women, that people with a high intuitive thinking style are less risk-averse than those with a low intuitive thinking style, that people with a high rational thinking style are more risk-averse than those with a low rational thinking style, and that respondents with a high sensation-seeking style behave in a more risk-seeking way than those with a low sensation-seeking style. In other words, women and people with a low intuitive thinking style, a high rational thinking style, or a low sensation-seeking style will take more cautious decisions regarding investments when coming to a choice between production and prevention in the case of type II risks.
4.8 Costs and Benefits and the Different Types of Risk
The optimum degree of safety required to prevent losses is open to question, both from a financial and economic point of view and from a policy point of view. As explained previously, developing and executing a sound prevention policy involve prevention costs, but remember that the avoidance of accidents and damage leads to hypothetical benefits. Consequently, in dealing with safety, an organization should try to establish an optimum between prevention costs and hypothetical benefits. This can be done by determining the minimum overall cost point (by calculating the prevention and the accident cost curves), but only if sufficient data are available, i.e. in the case of type I risks and accidents.
It is possible to further expand upon costs and benefits of accidents in general in terms of the degree of safety. The theoretical degree of safety can vary between (0 + ϵ)% and (100 − ϵ)%, wherein ϵ assumes a (small) value suggesting that “absolute risk” or “absolute safety/zero risk” in a company is, in reality, not possible. The economic break-even safety point, namely the point at which the prevention costs are equal to the resulting hypothetical benefits, can be represented in graph form (see Figure 4.15). The graph distinguishes between two cases: type I and type II risks. In the case of type I risks, the hypothetical benefits resulting from non-occurring accidents or non-events are considerably lower than in the case of type II risks, especially if the definition of Maxmax hypothetical benefits is used. This means essentially that the company reaps greater potential financial benefits from investing in the prevention of type II accidents than in the prevention of type I accidents. When calculated, prevention costs related to type II risks are, in general, also considerably higher than those related to type I risks. Type II accidents are mostly prevented by means of expensive technical studies and the furnishing of (expensive) technical state-of-the-art equipment and maintenance. Type I accidents are therefore more associated with the protection of the individual, first aid, the daily management of safety codes, and so on.

Figure 4.15 Economic break-even safety points for the different types of risk (qualitative figure).
(Source: Meyer and Reniers [73] Reproduced with permission from De Gruyter.)
As the company invests more in safety, it can be assumed that the degree of safety within the company will increase. Moreover, the higher the degree of safety, the more difficult it becomes to improve upon this (i.e., to increase it) and the curve depicting investments in safety thereafter displays asymptotic characteristics. This was also explained before. Moreover, as more financial resources are invested in safety from the point of (0 + ϵ)%, higher hypothetical benefits are obtained as a result of non-occurring accidents or non-events. These curves will display a much more level trajectory due to the fact that marginal prevention investments do not produce large additional benefits in non-events. The hypothetical benefits curve and the prevention costs curve dissect at a break-even safety point. If there are greater prevention costs following this point, hypothetical benefits will no longer balance prevention costs. A different position for the costs and benefits curves can be expected for the different types of accident.
It should be noticed that in order to calculate the hypothetical benefits of type I risks, the focus can be placed either on the consequences, or on the consequences as well as the probabilities (if those probabilities are available; cf. definitions (i) and (ii), respectively, in Section 4.2.4). They will clearly produce different curves. In the case of calculating the hypothetical benefits of type II risks, this can also be done, but as probabilities are much less reliable for such risks, and as people perceive the consequences of such risks as much less acceptable, it may be advisable to place more focus on the consequences. The calculation of hypothetical benefits has already been discussed in this chapter, but the concrete avoided costs leading to the hypothetical benefits will be explained more in depth in Chapter 5.
Figure 4.15 illustrates the qualitative benefits curves for the different types of risk. It is clear that hypothetical benefits and prevention costs relating to type I risks are considerably lower than those relating to type II risks. The break-even safety point for type I risks is likewise lower than that for type II risks. Figure 4.15 also shows that in the case of type II risks where a company might be subject to extremely high financial damage, the hypothetical benefits are even higher and the break-even safety point is likely to be located near the (100 − ϵ)% degree of safety limit. This supports the argument that in the case of such risks, almost all necessary prevention costs can be justified and zero type II risk should be strived for: the hypothetical benefits are nearly always higher than the prevention costs of such type II events.
Thus for type II risks, it is possible to state that a very high degree of safety should be guaranteed in spite of the cost of corresponding prevention measures. Of course, the uncertainties associated with these types of accident are very high, and therefore, economic analyses of such events can nevertheless be justified. Managers are not always convinced that such a major accident might happen in their organization, which is the main reason why the necessary precautions are not always taken, and why organizations are not always prepared. Therefore, economic analyses can be carried out for such events, but they should be different from those carried out for type I events and their results should be treated with a lot of caution and reservation.
In the case of type I risks, regular economic analyses such as cost-benefit and cost-effectiveness analyses may be carried out, and the availability of sufficient data should lead to reliable results, based on which “optimal” (and rational) safety investment and precaution decisions can then be taken.
4.9 Marginal Safety Utility and Decision-making
As explained earlier, safety utility can be regarded as the satisfaction that safety management receives from a certain safety situation or state thanks to operational safety measures. When the utility concept was explained in Chapter 3, the overall utility of a safety state, and its accompanying operational safety measures, was assumed. Nonetheless, the increase in (overall) safety utility as a result of the increase in one extra unit of operational safety state, a concept called the “marginal safety utility,” should be central to safety decision-making. Usually, the overall safety utility does not give any indication as to what optimized decisions to make regarding, for instance, extra safety measures. The marginal safety utility providing information about the additional satisfaction obtained from applying an additional safety measure does so.
Similar to any other goods and services, also in safety science, the marginal safety utility of a certain type of safety measure decreases when applying more of this type of safety measure (assuming ceteris paribus; i.e., all the other types of safety measures stay the same). Sometimes it is possible that the marginal utility initially increases, and only afterwards decreases. Usually, most goods are characterized by a very prompt stage of decreasing marginal utility.
Looking at the engineering factors of safety from The Egg Aggregated Model (TEAM) of Chapter 2, three types of observable operational safety measures exist to improve safety: technological safety measures, organizational/procedural safety measures, and personal safety measures related to human factors (“TOP”). Sometimes, strategic safety measures are explicitly mentioned, as they are applied at the design stage to achieve inherent safety. With strategic measures included, the acronym becomes “STOP” (a term originating from the DuPont chemical company). To explain the relationship between marginal safety utility and decision-making, we assume that only an optimal allocation of the TOP measures, for the purposes of add-on safety, is strived for.
If, for example, technological safety measures are focused on, the principle is illustrated in Table 4.7. Assume that one technological measure costs, on average, €200.
Table 4.7 Utility and marginal utility: an illustrative example
| Number of technological safety measures | Total safety utility of technological safety measures | Marginal utility of technological safety measures | Marginal utility of technological safety measures per euro |
| 0 | 0 | — | — |
| 5 | 1000 | 200 | 1 |
| 10 | 1800 | 160 | 0.8 |
| 15 | 2500 | 140 | 0.7 |
| 20 | 2900 | 80 | 0.4 |
In case of the illustrative example given in Table 4.7, the marginal utility associated with an increase from 0 to 5 units of technological measures is 200; from 5 to 10 units it is 160; from 10 to 15 units it is 140; and from 15 to 20 units it is 80. These numbers are consistent with the principle of diminishing marginal utility. As more and more technological safety measures are applied, additional amounts of such measures will yield smaller and smaller additions to safety utility, or smaller and smaller returns on investment. To make the illustrative example more concrete for the reader, it is possible to look upon the number of technological safety measures as the amount of the safety budget spent on technological safety measures, and the safety utility can then be compared with safety benefits obtained. Using these interpretations, it is possible to draft Figure 4.16.

Figure 4.16 Law of diminishing marginal rate of return on investment for technological safety measures.
Fuller and Vassie [70] indicate that safety measures do indeed show a diminishing marginal rate of return on investment: further increases in the number of a type of safety measure become ever less cost-effective, and the improvements in safety benefits per extra safety measure exhibit a decreasing marginal development. In other words, the first safety measure of the “technology” type provides most safety benefit; the second safety measure provides less safety benefit than the first, and so on. Hence, to be most efficient there should be safety measures chosen from different types (technology, organization/procedures, and people/human factor). Of course, there may be differences in the safety benefit curves for the different types of safety measures. Figure 4.17 shows the increased safety benefits from choosing a variety of safety measures.

Figure 4.17 Allocation strategy for the safety budget.
(Source: Meyer and Reniers [73]. Reproduced with permission from De Gruyter.)
Figure 4.17 shows that, if the total budget available is spread over a range of technology-, organizational/procedures-, and people/human factors-related safety measures, the overall safety benefit can be raised from point A (only investment in technology-related safety measures) in Figure 4.17 to point B (investment in TOP-related safety measures) in Figure 4.17. Hence, spreading the safety budget over different types of safety measures is always more efficient and effective than only focusing on one type of safety measure. This “equal marginal principle” is an important concept in microeconomics. Utility maximization is achieved when the budget is allocated so that the marginal utility per euro of expenditure is the same for each type of safety measure.
The usefulness of this theory with respect to decision-making and safety budget allocation can be illustrated by a numerical example. First, the curve of diminishing marginal rate of return on investment needs to be determined for each type of safety measure. The form of such a curve is given by
The parameters a and b determine the exact shape of the curves. The parameter a indicates the maximum value that the curve is approximating. If, for example, the maximum safety benefit is normalized and set to be 100% or 1, then ![]() . For instance, if a = 0.5, then the maximum safety benefit displayed by this curve is 50%. It would be possible for safety experts to assess that technological measures can maximally lead to 50% of safety benefits, organizational measures to 20% of safety benefits, and human factor measures to 30% of safety benefits. Any other combination is also possible and depends on a number of factors such as, for example, the industrial sector and the safety measures already in place. The parameter b indicates how fast the curve is approximating the maximum value. The higher b is, the faster the curve approximates its maximum value. Obviously, b is a measure displaying the level of efficiency of the measures.
. For instance, if a = 0.5, then the maximum safety benefit displayed by this curve is 50%. It would be possible for safety experts to assess that technological measures can maximally lead to 50% of safety benefits, organizational measures to 20% of safety benefits, and human factor measures to 30% of safety benefits. Any other combination is also possible and depends on a number of factors such as, for example, the industrial sector and the safety measures already in place. The parameter b indicates how fast the curve is approximating the maximum value. The higher b is, the faster the curve approximates its maximum value. Obviously, b is a measure displaying the level of efficiency of the measures.
4.10 Risk Acceptability, Risk Criteria, and Risk Comparison – Moral Aspects and Value of (Un)safety and Value of Human Life
Before explaining cost-benefit analyses in the next chapter, there are some important concepts that need to be clarified. Difficult questions that will arise when carrying out economic analyses include, for instance, what is an “acceptable risk”; is it possible to put a value on everything, even on human life; what are possible risk criteria; and is it possible to compare completely different risks with one another? These issues are discussed in this section.
4.10.1 Risk Acceptability
Risk acceptability is an extremely difficult and complex issue. The problem starts with the questions, acceptable for whom, and from whose perspective? In other words, who suffers the consequences when something goes awfully wrong and disaster strikes, on the one hand, and who gains the benefits when all goes well and profits are made, on the other? Are the risks equally spread? Are the risks justified/defensible and, even more importantly, are they just? Moral aspects always start to emerge when discussing the acceptability of risk, in other words, when asking the question “how safe is safe enough?”
Independent of the personalities of people, the discussion and debate about what risks and levels of risk are acceptable continues. Some people argue that one fatality is one too many, and others interpret the prevailing accident rate in areas of voluntary risk-taking as a measure of the level of risk that society as a whole finds acceptable [103]. Obviously, both viewpoints have their merits. No one will argue against the fact that one death is one too many. But it also seems reasonable to assume that voluntary risk levels can be used as some sort of guideline for involuntary risk levels. However, both perspectives are far from usable in the real industrial world. On the one hand, lethal accidents do happen and should not be economically treated as if they were not possible. So being part of industrial practice and real-life circumstances, fatalities should be taken into account in economic analyses. On the other hand, research indicates that voluntary risk cannot be compared with involuntary risk. People are much less willing to suffer involuntary than voluntary risks, and the risk perception that people have about involuntary risks is much higher than that about voluntary risks [104]. Hence, these two sorts of risk (i.e., voluntary and involuntary risks) should not be used interchangeably in economic analyses, and risk criteria should not be based on them.
In this book, risks and dealing with risks are viewed from a microeconomic decision-making perspective. Hence, the focus is on the optimal operational safety decision, based on the information available and thereby taking economic issues into account. Risks are relative, and making the best resource allocation decision for operational safety in a company means avoiding as much possible loss as possible within a certain safety budget. However, due to the “acceptability” aspect of risks this seems easier than it is in reality. One of the best known and most used principles in this regard is the proactive concept of “as low as reasonably practicable” (ALARP). The term implies that the risk must be insignificant in relation to the sacrifice in terms of money, time, or trouble required to avert it. Hence, ALARP means that risks should be averted unless there is a gross disproportion between the costs and the benefits of doing so. The difference between ALARP and other terms such as “best available technology” (BAT), “best available control technology” (BACT), and “as low as reasonably achievable” (ALARA) can best be described as the observation that to follow the ALARP approach, not only should the technology be available, but also the costs of prevention should be reasonable. BAT and ALARA demand to do work, research, engineering, and so on, to make the prevention work, irrespective of the costs. The term “so far as is reasonably practicable” (SFAIRP) is used in health and safety regulations in the UK, and should not be confused with ALARP, which has no legislative connotation. The SFAIRP term has been defined in UK courts. The formal definition given by Redgrave [105] is:
‘Reasonably practicable’ is a narrower term than ‘physically possible’, and implies that a computation must be made in which the quantum of [operational] risk is placed in one scale and the sacrifice involved in the measures necessary for averting the risk (whether in money, time or trouble) is placed in the other, and that, if it be shown that there is a gross disproportion between them – the risk being insignificant in relation to the sacrifice – the defendants [persons on whom the duty is laid] discharge the onus upon them [of proving that compliance was not reasonably practicable]. Moreover, this computation falls to be made by the owner at a point of time anterior to the accident.
An acronym similar to ALARP (but with slightly different meaning as regards the word “reasonable”) is “best available technology not entailing excessive costs” (BATNEEC). Other acronyms focusing on the legislative (and reactive) part are “cheapest available technology not invoking prosecution” (CATNIP) and “as large as regulators allow” (ALARA – second meaning) .
It is clear that there is a diversity of acceptability approaches out there, but the most well known and the most used is undoubtedly ALARP. ALARP is also the most useful on an organizational level, as the risk level of being ALARP is influenced by international guidelines and directives, the progress of societal knowledge of risk, the continuous evolution of people's perception of what “risk” constitutes, political preferences and other forms of regulation in different industries. Hence, the ALARP principle allows us to have a different risk judgment depending on industrial sectors, risk groups, risk-prone areas, and even organizations.
The relationship between the ALARP principle and the terms “intolerable,” “tolerable,” “acceptable,” and “negligible risk” is illustrated in Figure 4.18.

Figure 4.18 The “as low as reasonably practicable” (ALARP) principle and its relationship with the terms “intolerable,” “tolerable,” “acceptable,” and “negligible.”
Figure 4.18 shows that it is possible to distinguish between “tolerable” and “acceptable.” The subtle distinction between both terms is used to indicate that a level of risk is never accepted, but it is tolerated in return for other benefits which are obtained through activities, processes, and so on, generating the risk [106]. Figure 4.18 illustrates that the activities characterized by high levels of risk are considered intolerable under any normal circumstances. At the lower end, there is a level below which risk is so low that it can be ignored – i.e., it is not worth the cost of actively managing it. There is a region between these two limits, called the ALARP region, in which it is necessary to make a trade-off between the risk and the cost of further risk reduction.
The practical use of ALARP within one single organization can be demonstrated by using the risk assessment decision matrix (see also [73]). The goal of all reduction methods is summarized in Figure 4.19, where one can observe that risks that are considered unacceptable (with the visual help of the risk matrix) have to be brought down to an acceptable level or at least to one that is tolerable.

Figure 4.19 The “as low as reasonably practicable” (ALARP) principle and the effect of risk reduction represented in the risk matrix.
In the middle zone of the matrix, two intermediate regions, “2” and “3”, between the unacceptable zone “1” (needing immediate action) and the negligible zone “4” can be noted in diagonal. These zones are the ones where the ALARP principle occurs. Using the risk matrix, it is thus easily possible for an organization to make a distinction between the tolerable region “2” and the acceptable region “3” as noted in Figure 4.19, and to link certain actions to it, specifically designed by and for the company.
In any case, the ALARP principle needs a decision rule (or criteria) specifying what is “reasonable” for the person, group of persons, or organization using it. The decision will ultimately depend on a combination of physical limits, economic constraints, and moral aspects. The advantage is that the principle works in practice, but the downside is that it will sometimes lead to inconsistencies in effective valuation of various risks, and have inefficiencies in the sense that it may be possible in some cases to save more lives at the same cost, or the same number of lives at a lower cost [74]. The next section discusses some criteria that are widely used to make decisions using ALARP.
There are a number of disadvantages or issues concerning the using of economic (e.g., cost-benefit) analyses for ALARP. For example, there is a difference between the willingness to pay (WTP) and willingness to accept (WTA) evaluations (see also Section 4.10.4.3), both approaches that are often used to put values on (un)safety. There are also problems of understanding “gross disproportionality” and of putting a value on human life. Furthermore, sometimes risks are only replaced by (exported to) another facility not falling under the same (or under any) ALARP calculation.
4.10.2 Risk Criteria and Risk Comparison
Risk criteria are related to the definition of risk and the target exposed to the risk. Within a single organization, there can be a number of possible targets: employees, groups of employees, material assets of the company, non-tangible assets of the company (such as reputation, image), intellectual property of the company, and also surrounding communities and the society as a whole.
As this book is only concerned with operational risks, and not, for example, with voluntary risks, natural-technological risks, or terrorist risks, no policy factor varying with the degree to which participation in the activity is voluntary and with the perceived benefit needs to be introduced into the risk calculation. All operational risks are in essence involuntary, for citizens living nearby the industrial activity but also for the employees working at the organization. However, there is a difference between a company's employees and its surrounding communities: i.e., the benefits arising from the industrial activity. The perceived risk will thus be different between both groups of people. This is the problem of equity or distribution of risk. Those people who take the risk are often not the same as those who bear the risk. As Ale et al. [107] indicate, when the rewards of risk-taking go to the risk creators and the costs are carried by the risk bearers, a strong incentive is created for a small group to take large risks at the expense of others. Moreover, the increase in productivity, turnover, and/or profits as a total may be maximized, but some employees may have more profit than others while bearing less risk. Therefore, this moral aspect should be considered when carrying out an economic analysis and establishing risk criteria. Section 4.10.4 treats this question in more depth.
If one considers only human losses (injuries and fatalities), there are different possible approaches to calculating risk (using a strictly rational point of view), to subsequently base the necessary risk criteria on human-related risks. Two very well-known approaches that are widely used are the calculation of the “location-based (individual) risk” and the “societal risk.” An individual risk provides an idea of the hazardousness of an industrial activity. A societal risk takes the exposure of the population in the vicinity of the hazardous activity into account in the calculation.
4.10.2.1 Location-based (Individual) Risk
An individual risk can be defined in general as “the frequency with which a person may expect to sustain a specified level of harm as a result of an adverse event involving a specific hazard.” Hence, the individual risk can be used to express the general level of risk to an individual in the general population, or to an individual in a specified section of the community. Legislators often use levels of individual risk with “specified level of harm” equal to “fatality” (such risks should actually be called “individual fatality risks”) as a regulatory approach to setting risk criteria. In the process industries, for example, the individual (fatality) risk is defined as “the risk that an unprotected individual would face from a facility if he/she remained fixed at one spot 24 hours a day 365 days per year.” Therefore, the risk is also sometimes called location-based (individual) risk. A location-based risk describes the geographic distribution of individual risk for an organization. It is shown using so-called iso-risk curves, and is not dependent on whether people or residences are present (see Figure 4.20).

Figure 4.20 Example of iso-risk curves showing the distribution of location-based (individual) risk surrounding an enterprise.
Location-based risk is used to assess whether individuals are exposed to a greater than acceptable risk in the locations where they may spend time (e.g., where they live or work). It does not directly provide information on the potential loss of life, nor does it distinguish between exposure affecting employees and the general (surrounding) population. In many countries, an additional fatality risk from industrial activities of 10−6 (1 per million)/year to a person exposed to this fatality risk is considered to be a very low level compared with risks that are accepted every day, and hence used as a risk criterion. The reasoning for this risk criterion is based on what is known about risk perception. On the one hand, the individual risk of being killed while driving a car is estimated (very generally) as 10−4/year. If the level of (individual) risk is higher than driving a car, it is perceived as unacceptable. On the other hand, the individual risk of being struck by lightning is estimated as 10−7/year, and this risk level is perceived (in general) to be so low that it is acceptable.
Risks of the same type can thus be compared with one another to agree upon a risk criterion. There are actually a number of reasons for comparing risks with each other. The most important reason might be that by comparing risks, it is possible to improve the understanding and the perception of risks, both by the general public and by experts. It is difficult to grasp the meaning of “one in a million,” although people do tend to have a natural feeling and intuition for categorizing risks into low–medium–high, for example. By comparing lesser known risks with more familiar risks, the familiarity and understanding of known or older risks can be transferred to new and unknown risks. Table 4.8 helps to place different risks in perspective, by quantifying the one-in-a-million (10−6) risk of dying from various activities.
Table 4.8 Some “one-in-a-million” risks of dying from various activities
| 1. Smoking two cigarettes (risk of heart disease included) |
| 2. Eating 100 g servings of shrimp |
| 3. Eating 35 slices of fresh bread |
| 4. Eating 350 slices of stale bread |
| 5. Eating one-half basil leaf (weighing 1 g) |
| 6. Drinking 70 pints of beer in 1 year |
| 7. One-quarter of a typical diagnostic chest X-ray |
| 8. A non-smoker living in a home with a smoker for 2 weeks |
All of these risks are risks relevant to adults consuming this amount. Children consuming half this amount would be at comparable risk.
Wilson and Crouch [74]
Individual fatality risks in an industrial context are calculated by multiplying the consequences and the frequency of undesired events. For example, if the severity of an industrial accident is such that there is a probability p of killing a person at a specified location [the probability merely takes into account the level of lethality due to the accident (e.g., due to heat radiation or due to a pressure wave), but does not consider population figures], and the accident has a annual frequency of f, then the individual fatality risk at this particular location due to this event is p × f per year. Where there is a range of incidents that expose the person at that point to risk, the total individual fatality risk is determined by adding the risks of the separate incidents/events.
Contours of identical risk level (such as those in Figure 4.20) can then be plotted around an industrial activity, and can be used to present the risk levels surrounding the activity. Different levels of individual fatality risk can then be used by companies to discern between different company sites. A distinction can be made, for example, among production areas, administration areas, commercial areas, parks and fields, fire department, and care units .
4.10.2.2 Societal Risk or Group Risk
Calculating the individual fatality risk around a specific industrial activity does not make a distinction between, for example, the activity taking place somewhere in the desert or in a major city center. The calculated individual risk will be the same, regardless of the number of people exposed to the activity. However, it is evident that in reality the level of risk will not be identical in both situations: the level of risk will be higher if the industrial activity takes place in the city, rather than in the desert. This is a result of people living in the neighborhood of the activity, and thus being exposed to the danger. To take the exposed population figures into account, a so-called societal risk is calculated. The societal risk, also called group risk, is defined as “the probability that a group of a certain size will be harmed – usually killed – simultaneously by the same event or accident” [108]. It is presented in the form of a so-called “FN curve.” Each point on the line or curve represents the probability that the extent of the consequence is equal to or larger than the point value. These curves are found by sorting the accidents in descending order of severity, and then determining the cumulative frequency. As both the consequence and the cumulative frequency may span several orders of magnitude, the FN curve is usually plotted on double logarithmic scales. A log–log graph as depicted in Figure 4.21 is obtained. For a concrete example on how to calculate and plot an FN curve, see Section 4.11.2.3.

Figure 4.21 Illustrative example of an FN curve.
The different steps in Figure 4.21 show the probabilities (cumulative frequencies) of different scenarios. The societal risk is designed to show how risks vary with changing levels of severity. FN curves are therefore often used for comparison with a “boundary line” representing a norm following legislation. This boundary line is also called the societal risk criterion. As an example, a boundary line fixed by Flemish law is given in Figure 4.21. This type of boundary was originally proposed by Farmer in 1967, as explained in Duffey and Saull [109], in a paper that launched the concept of a boundary line for use in the probabilistic safety assessment of nuclear power plants. The boundary line actually represents the transition region between the tolerable region and the unacceptable region. For example, in theory (not taking moral aspects into consideration at this time), a hazard may have an acceptable level of risk for 20 fatalities, but may be at an unacceptable level for 100 fatalities. Usually, such a boundary line, if it exists, is determined by the authorities, but it can also be fixed by individual companies for internal use.
In some jurisdictions, there are two defined boundaries (societal risk criteria) on the FN graph, i.e., separating the zones of high risk (unacceptable region), intermediate high risk (tolerable region), and intermediate low risk to low risk (acceptable region and negligible region) (see also Meyer and Reniers [73]). It is common, where an industrial activity is calculated to generate risks in the tolerable region, to require the risks to be reduced to an ALARP level (see also the previous section), provided that it can be proved in some way that the benefits of the activity that produces the risks are seen to outweigh the generated risks.
Mathematically, the equation for an FN risk criterion may be represented as [110]:
or:
where F is the cumulative frequency of N or more fatalities; N is the number of fatalities; a is an aversion factor (usually between 1 and 2); and k is constant. From the equation, it is clear that the slope of the societal risk criterion (when plotted on a log–log basis) is a and represents the degree of aversion to multi-fatality events embodied in the criterion:

For instance, if a = 1, the frequency of an event that results in 100 fatalities or more should be 10 times lower than the frequency of an event that results in 10 or more fatalities. If a = 2, the frequency of an event that results in 100 or more fatalities should be 100 times lower than the frequency of an event that results in 10 fatalities or more.
In enterprises encountering numerous hazards with severe potential consequences, computer programs are used to calculate the risk levels on a topological grid, after which they are used to plot contours of risk on the grid. These contours are used to display the frequency of exceeding excessive levels of hazardous exposure. For example, Reniers et al. [111] indicate the availability of software tools that will prepare contours, for example, for the frequency of exposure to nominated levels of heat radiation, explosion overpressure and toxic gas concentration. So-called quantitative risk assessment (QRA) software is used to plot FN curves.
One should keep in mind that all these software tools provide an insight into the possible scale of a disaster and the possibility of its occurrence, but they do not offer adequate information for the optimal prevention of catastrophic accidents. Moreover, if the number of events observed in the past is not sufficient to estimate significant frequency values, as in the case of type II events, a simple histogram plotting the absolute number of past events versus a certain type of consequence is often used instead of a risk curve. However, type II event predictions are extremely difficult to make, simply because of the lack of sufficient data. Although it is therefore not possible to take highly specific precautions based on statistic predictive information in such cases, engineering risk management leading to a better understanding of relative risk levels and to an insight into possible accident and disaster scenarios is essential to prevent such disastrous accidents and should therefore be fully incorporated into industrial activities worldwide.
From the previous paragraph, it can thus be argued [109] that the uncertainty about the events should be given much more emphasis in risk criteria and trade-offs. Actual outcome data from major catastrophes in modern society indicate that the desired risk levels are often not achieved, and that the actual outcomes have greater uncertainty and hence higher risk. Concrete examples are: the Concorde aircraft crash with over 100 fatalities over 27 years of operation; the Columbia and Challenger shuttle losses with 14 fatalities over an interval of 17 years between the flights; the Texas city refinery explosion with 15 fatalities over about 30 years of operation; the Chernobyl reactor explosion with 30 fatalities directly, and many more indirectly, over 30 years of plant life.
In any case, Sunstein [112] mentions that as the severity of an event increases, people become more risk-averse. In particular, once the death threshold is passed, it appears that the community has a much greater aversion to multiple fatality accidents. This is the reason why the aversion factor is often chosen to be higher than 1. The public in general is risk-averse, or, more accurately, consequence-averse, meaning that more severe consequences (with the same frequency) weigh heavier in the decision-making process than more frequent events (with the same total consequence).
In fact, there has been an ongoing debate about giving equal weight to the frequencies and consequences of accidents. By not distinguishing between one accident causing 50 fatalities and 50 accidents each causing one fatality over the same period of time of operation, one fails to reflect the importance society attaches to major accidents. Evans and Verlander [113], for example, claimed that the economic rule of constant utility (iso-utility) was violated by choosing an aversion factor higher than 1, and that therefore decisions made on any other criterion than the expectation value (EV) of the number of victims is wrong. However, recently Bedford [114] showed that an FN curve with an aversion factor higher than 1 is not risk-averse but consequence-averse, and thus no economic laws are violated. Nonetheless, as Ale et al. [107] mention, multiple fatalities can create greater disutility than single fatalities. Obviously, 30 people killed in a major explosion at a chemical plant operating for 20 years will lead to social debate and parliamentary enquiries, while the same number killed on the road in 20 days does not cause any societal ripple.
Linking the multiple fatality aversion with an economic analysis approach is rather difficult. This was demonstrated by the European Commission cost-benefit analysis results, indicating that the live-saving benefits of safety case regimes disappeared from view because the monetized value of life (VoL) (see Section 4.10.4) lost in major accidents was insignificant in comparison to other costs. Nonetheless, disasters can (and often will) result in multiple fatalities, and an economic analysis ignoring this fact is clearly problematic. Sunstein [112] therefore argues that preventing major accidents cannot be based on conventional cost-benefit analyses of lives lost. In fact, a rule of thumb is that 10 fatalities occurring at the same time are 100 (102) times worse than one death, and 100 fatalities at the same time are 10 000 (1002) times worse than one fatality [115]. This can be translated into monetary values in the following way. Assuming that it is possible to put a value on human life (see Section 4.10.4 for more details), and that the value is €10 million, then the value of 10 lives lost at the same time equals €1 billion, and the value of 100 lives lost together equals €100 billion, and so on. By treating single fatalities differently from multiple fatalities for assigning monetary values, such a rule of thumb could obviously make a big difference in cost-benefit calculations. However, organizations should decide for themselves whether or not to use such a rule of thumb (or a similar one). In any case, it is a means to take into consideration the public's disaster aversion, and to recognize as a company that multiple deaths would affect society – and also the company itself – far more than the multiple would suggest.
Moreover, it is worthwhile mentioning a special case, i.e., the observation that several industrial activities from nearby companies in the same industrial area may each generate a low level of societal risk, each falling in the acceptable region, whereas their combined societal risk might fall within the high-risk zone (unacceptable region) of the chart in Figure 4.19, if these industrial activities were all to be grouped for the purposes of the calculation. As society places a special value on the prevention of large-scale loss of life, such multiple plant disasters should also be considered when carrying out economic analyses. However, this falls outside the scope of this book, which is concerned with operational safety economics within single organizations.
4.10.3 Economic Optimization
The relationship between risk criteria and an economically optimal situation can also be formulated as an economic decision problem, analogous to the method proposed by van Danzig [116] for flood defenses and by Jonkman et al. [117] for tunnel safety. In view of economic optimization, the total (hypothetical) safety benefits of a system (HBtot) are determined by calculating the expected hypothetical benefits due to safety investment costs (SIC), that is, E(HBSIC), and then subtracting these SICs (or expenditure for a safer system) from these expected hypothetical benefits. In the optimal economic situation, the total hypothetical benefits in the system are maximized:

Assuming that the SICs and the expected hypothetical benefits are both a function of a probability of loss, Ploss (e.g., the probability of dying combined with the probability of failure), it is possible to determine the optimal probability of loss of a system, subject to the condition of a predefined risk criterion. Moral aspects such as equity or justification of risk can then be taken into account in defining the risk criterion by the organization (see also Section 4.10.4).
For a thorough discussion of the SICs and the hypothetical benefits, see Chapter 5. When the probabilities of different accident scenarios are known, the expected hypothetical benefits can thus be assessed, and the optimal safety investments can be derived within the bounds of a predefined risk criterion. Obviously, although it is possible to take only material damage into the valuation problem, it is sometimes necessary, and therefore it should also be possible, to take the value of human life into the economic optimization problem. However, the valuation of safety and the valuation of human life both raise numerous ethical and moral questions, and they have been a subject of the safety literature for decades. The next section treats these sensitive subjects in more detail.
4.10.4 Moral Aspects and Calculation of (Un)safety, Monetizing Risk and Value of Human Life
4.10.4.1 Moral Aspects and Calculation of (Un)safety
This section on moral aspects and the calculation of safety, together with the next section on the monetizing of risks and the valuation of human life can be seen as the most difficult sections of the entire book. They are not difficult because of the mathematical formulae involved, but rather because the sections are highly complex due to the very important moral aspects interweaved with the questions of calculation of safety and valuation of human life. This ethical dimension may quickly turn into a philosophical discussion with very diverse viewpoints and opinions. Needless to say, the topic is highly debated, controversial, and sensitive to many people. That being said, a book on the economics of operational safety cannot simply omit or gloss over the moral aspects, or the valuation of human life, as something trivial in the calculation of safety. A thorough discussion and a viewpoint are thus needed. This section delivers just that.
As noted by van de Poel and Fahlquist [118], the psychological literature on risk perception has established that laypeople include contextual elements in how they perceive and understand risks (e.g., Slovic [104]). Such contextual elements include voluntariness, familiarity, dread, exposure, catastrophic potential, controllability, perceived benefits, and time delay (future generations). The fact that there is a difference in risk perception between laypeople and experts is often interpreted as the result of the irrationality of laypeople. However, such an interpretation indirectly assumes that the expert opinion, or the technical conceptualization of risk, is the correct one and that laypeople should simply be educated to the same viewpoint. However, Slovic [104] and Roeser [119, 120] explain that the contextual elements considered by laypeople are actually relevant for a better perception of the reality of risk, and are thus important for the acceptability of risks and for adequately managing risks.
Sunstein [121] notes that when asked to assess the risks and benefits associated with certain items, people tend to think that hazardous activities contain low benefits, whereas beneficial activities contain low hazards. Rarely do people consider an activity to be both highly beneficial and hazardous, or to be both benefit-free and hazard-free. Slovic [122] even suggests a so-called “affect heuristic,” by which people have primarily an emotional reaction to certain situations, processes, activities, products, and so on. It follows that emotions and feelings are essential elements to consider when dealing with operational risks and appreciating operational safety. Besides objective consequences and probabilities of potential scenarios, moral aspects (possibly fed by emotions) should thus play an important role in the calculation of safety. The subsequent activities of hazard identification, risk analysis (including estimation/calculation of consequences and likelihood), risk evaluation, and risk prioritization, the process known as risk assessment, only serve provide a rational idea of all the prioritized (rational) risks (for a certain scope of the safety study), in order to make decisions about what risks to deal with first, second, and so on (hence, safety budget allocations). However, to improve the safety budget allocation decision process, more than just rational risk prioritizations should be carried out; safety appreciation prioritizations should also be executed, where moral aspects are taken into account as well as the rational aspects.
If moral aspects were considered in the safety calculation process, economic analyses would perhaps be much less contested or debated, and more accepted as a valid approach to ensure that company policy is driven not by pure ratio or pure emotion, but by a combination of both, and thus a full appreciation of all aspects of safety, rational as well as emotional, is strived for. The risk thermostat, originally developed by Wilde [123] and adapted by Adams [103, 124, 125], can be applied to an organization, and the importance of balanced safety appreciations becomes immediately obvious in this regard. This is explained in the following paragraphs.
Everyone, including decision-makers in companies, has a propensity to take risks within appropriate limits. This propensity varies from one company to another and is influenced by the potential level of the rewards and losses arising from the organization's risk-taking decisions. Companies' so-called “perceptions of risk” are determined by the safety appreciations carried out in the company. Furthermore, companies' risk policies represent a balancing act in which the perceptions of risk are balanced against the propensity to take risks. Benefits and losses arise from an organization taking risks, and the more risks (in general, thus also the more operational risks) an organization takes, the greater the potential level of costs and benefits. Figure 4.22 shows this risk thermostat model applied to organizations.

Figure 4.22 The risk thermostat model applied to organizations.
(Source: Adams [103]. Reproduced with permission from John Wiley & Sons.)
The conceptual model illustrated in Figure 4.22 explains the impact of the safety appreciation process on the position of the company's risk policy balance. If moral aspects are not taken into consideration in the safety calculation, and, as a result, the costs from the company's risk policy are determined to be quite low (compared with the possible costs for the company if moral aspects were taken into account), the perception of a certain risk (e.g., a HILP risk) will be low, and the balance will tend toward risk-seeking behavior. In the case of type II risks, in particular, the risk thermostat conceptual model shows the importance of safety calculations taking moral aspects into account.
The literature ([126–130]) indicates the moral concerns that are often mentioned: voluntariness, the balance and distribution of benefits and risks (over different groups and over generations), and the availability of alternatives. These ethical dimensions can be used to enlarge the technical conception of operational risk, given in Chapter 2, in an extended formula of a “qualitative and quantitative” risk index, a so-called Q&Q risk index. The following formula for the Q&Q risk index (R*) is proposed to this end:
where

It is important to realize that the risk aversion factor a should be seen as a general factor for people with respect to their aversion to the consequences of risks, whatever the nature and background of the risks. The factors determining the acceptability, A, of a risk, however (i.e., F, E, and b), are risk-specific and depend on the nature and background of the risk. The factors E and F are also mentioned and defined by Rayner [131] in an early attempt to extend the well-known rational risk formula R = L × C. In the formula for an operational risk index that is proposed above, rationally calculated risk is combined with emotional aspects to determine a proxy for operational risk within an organization. E is a parameter representing the moral principle of “equity,” taking the emotions concerning the balance and distribution of benefits and risks into consideration. F is a parameter providing an idea of the moral principle of “fairness” or justification related to the operational risk of an event or scenario. Using this formula, the Q&Q risk index, R*, of an undesired event (or the risk of an event happening) is lower the more acceptable this event is, the higher the voluntariness of suffering the risk accompanying the event, and the lower the rationally calculated risk. As β and A are both dimensionless numbers, this R* index is expressed in the same units as rational risk. Hence, if rational risk is expressed in monetary units per time units (e.g., €/year), R* is also expressed in these units. The R* index could thus be used as an approach to calculate risk within an organization, using both the well-known rational data such as probabilities, consequences, and exposure, and the less frequently used moral principles such as fairness, equity, and anti-recklessness of management.
If company management wanted to use this approach, it would have to quantify the factors, E, F, a, and b. Notice that the parameters β, E, and F should be expressed as indices, and numbers for each of these parameters should be sufficiently different from each other to be relevant in the formula. A protocol within the company or within society should be designed to unambiguously determine the approach to quantify every parameter. Notice that if it were possible that a parameter β, E, or F could be chosen to be zero, then the R* level for the event would be infinite, and thus the event could never be made safe enough, whatever the safety investments to influence (lower) the likelihood and/or consequences. Therefore, this possibility is best excluded.
As an example, the following qualitative indices could be suggested for the parameters β, E, and F:
- Very low – 0.1
- Low – 0.5
- Medium – 1.0
- High – 1.5
- Very high – 2.0.
The parameters a and b are also suggested to be situated in the interval [0, 2], to avoid stressing the aversion factor and the anti-recklessness factor too much in the risk formula.
The ![]() index can then be used to fix a (maximum) company risk criterion for the probability of loss (see also the previous section) by determining the maximum probability for a certain (company-specific) Q&Q risk level (as given/fixed by the maximum
index can then be used to fix a (maximum) company risk criterion for the probability of loss (see also the previous section) by determining the maximum probability for a certain (company-specific) Q&Q risk level (as given/fixed by the maximum ![]() number).
number).
Clearly, this example should only be seen as illustrative, showing how moral principles might be integrated into risk calculation and hence influence safety decision-making with respect to the allocation of safety budgets. The rational risk calculations will always be very important to obtain a thorough idea of the real situation with respect to risk prioritization, but moral principles can help to give new and thorough insights into of the perceived situation with respect to risk prioritization.
4.10.4.2 Micromorts – the “Units of Death”
The so-called “micromort” can be seen as a “unit of death,” as it is defined as a one-in-a million probability of death. Death can be sudden, or it can be chronic. As operational risks in this book are looked upon as being acute and not chronic (this is dealt with by health management), the micromort can be used in terms of acute death. A one-in-a-million probability of death can also be explained as throwing 20 coins simultaneously into the air and them all coming up heads in one go, which corresponds to the probability of a micromort (1 in 106 is roughly 1 in 220).
The micromort allows completely different risks to be compared with one another, as the units provide an idea of the riskiness of various day-to-day activities. For instance, if the risk of dying while carrying out a certain operation/task/handling in an organization is calculated to be 1 in 100 000, one can expect 10 fatalities in every million operations/tasks/handling carried out in the organization. This can be described as 10 micromorts per operation/task/handling. This number can then be compared with other average risks (which are perhaps more familiar to laypeople) such as traveling 160 km by bicycle or traveling 3700 km by car, which also corresponds to 10 micromorts. Micromorts can thus obviously be employed to compare and communicate small risks.
So a micromort can be seen as the average “ration” of lethal risk that people spend every day, and which they do not worry about unduly.
Another application of micromorts is the measurement of values that humans place on risk. Consider, for example, the amount of money one would have to pay a person to get him or her to accept a one-in-a-million chance of death, the so-called willingness to accept (WTA), or, conversely, the amount that someone might be willing to pay to avoid a one-in-a-million chance of death, the so-called willingness to pay (WTP; see also the following section). However, utility functions are often not linear, and the more that people have spent on their safety, the less they will be willing to spend to further increase their safety, and hence one should be very careful in upscaling numbers. A €50 valuation of a micromort does not necessarily mean that a human life (corresponding to 1 million micromorts) should be valued at €50 000 000. Conversely, if human life is valued at, say, €5 000 000 (see also the following section), this does not necessarily mean that a micromort value corresponds to €5. The concept becomes even more difficult to use if accidents are considered with a number of fatalities at once.
4.10.4.3 Monetizing Risk and Value of Human Life
The risk thermostat model applied to organizations, explained in the previous section shows how operational safety decisions come about. An organization's balancing risk policy is assumed to seek an optimal trade-off between the potential benefits and the potential costs induced by the risk policy. There is one problem though: costs and benefits are numerous, various, multifaceted, and often considered incommensurable. There is no established or accepted theory about the balancing act of an organization's operational risk policy. There is, however, a large body of literature in economics on cost-benefit analysis that insists that decisions can be rational only if they are the result of mathematical calculation in which all relevant considerations have been rendered measurable; the common unit for measurements preferred by economists is money.
The next chapter treats cost-benefit analyses in depth, but it is useful to indicate in this section that there may be some problems with monetizing risk, as is sometimes required for determining the costs and the benefits associated with operational safety decisions. As Adams [103] explains, the purpose of cost-benefit analyses is to produce a Pareto improvement, if possible. A Pareto improvement is a change that will make at least one stakeholder better off and no one worse off. As any operational safety project that will produce this result is rare to nonexistent, economists commonly modify the objective toward producing a “potential” Pareto improvement. Hence, the purpose is then that the “winners” of the safety project compensate the “losers” out of their winnings and in such a way that they would still have something left over. In order to answer this question, there is a need to compare, in some way, the winnings and the losses, leading to the concept of risk monetization.
However, not everything can be translated directly into monetary terms, e.g., body parts or human life. For those matters that cannot be monetized directly, it is assumed that their valuation into money can be inferred from the values of those matters that can be monetized directly. However, there is a lot of controversy and debate surrounding this topic. Kelman [132], for example, argues that the mere act of attaching a price to a quality or condition changes it fundamentally. He reasons that unpriced values (e.g., a hand that is lost due to an industrial accident) provoke solidarity, as they are directly rooted in the feelings and experiences shared among social beings; by introducing prices (e.g., €50 000 as the price of a hand lost) these things are reduced to the level of commodities about which people are socialized to respond to individualistically and even competitively. This is on a societal level. In an organizational setting, however – which is the focus of this book – and with the aim to provide inputs into company decision processes about taking various safety actions to reduce risks, this argument can be challenged. In organizations, employees have the goal of making profits. Hence, every working day they trade off all kinds of operational risks against the profits that are made through the company's activities. It would therefore be irrational for employees to respond differently to a risk or opportunity that they know well and that they deal with day by day (thus systematically), just because a number is attached to it. Employees within an organization have chosen to work within this particular organization, to carry out specific tasks, and to implicitly accept the risks of the activities in return for a paycheck. Another argument is that people make decisions, but they also have decisions made for them. This may be true, but in an organization, if safety is calculated as explained before (using moral aspects) and people are treated from the point of view of respect and self-leadership, the monetization of risks is possible/defensible/allowed .
Another way of looking at this is that monetizing risks in an organizational setting is all about measuring preferences, not about measuring intrinsic values of operational safety. Economic values and intrinsic values are different. The use of a monetary standard in an organization is convenient and should be looked upon from a pragmatic perspective, i.e., it is employed to measure relative values (as opposed to actual values, because they are incommensurable). The question that organizations really want to answer by using risk monetization techniques, is as follows: Are the benefits (accidents avoided) following the taking of safety measures big enough to outweigh the operational safety investment decisions (costs of safety actions), or not? The answer may then be used as one (but, of course, only one) input to a decision process. As Wilson and Crouch [74] explain, in many cases, the comparison between risks is easy. The risk may be so large that once it is perceived, it needs action; this is the case if the risks are situated in the unacceptable region. In another case, the risk may be so small that it is not worth the trouble thinking about what actions to take; this is the case if risks are situated in the negligible region. Such cases are not worth highlighting as there is no controversy. Still other risks may belong to one of these two regions, but they may not be perceived in this way, due to there being no calculations or incorrect calculations/perceptions. The challenge for company decision-making, however, lies in the risks belonging to the ALARP region.
The coefficient for the equivalent of a monetary cost of a risk inevitably causes controversy, argument, and debate. When used by a company, it should, however, be regarded as an approximation to the organization's safety management's idealized safety utility function. By using such a coefficient, the goal is to obtain a measure of the utility of a risk by assigning a numerical value per unit of risk, usually expressed in monetary terms. Let's refer to this coefficient as gamma (γ). The coefficient does not need to be a constant, independent of the size and nature of the risk. This is explained in the following.
Consider a risk R to a company. The value of γ is determined by the level of the risk, which in turn depends on the circumstances. Thus, γ is function of R, implying it should be written as γ(R). Besides being consistent with theories accompanying utility models and models of perception, it can easily be understood. Let's assume that a company has a fixed safety budget to spend, and all factors in the risk calculation formula are constant except for the probability p. Consider a company faced with a major accident scenario probability of, for example, one in a million (10−6)/year. The company would be prepared to invest a certain amount of the available (fixed) safety budget in order to tackle the risk. In case of a larger risk, e.g. of a probability of 10−4, the company may be willing to invest a proportionally larger amount of the available safety budget (in the example, 100-fold larger), in exchange for dealing with the risk. However, if the risk were to become high enough, the limit of the available fixed budget that can be employed for safety investments might be reached, and the amount per unit of risk should logically decrease thereafter. Figure 4.23 displays this γ(R) curve.

Figure 4.23 Safety investment (to deal with the risk) per unit of risk, in the case of a fixed safety budget.
All by all, every risk can be monetized in some way with finite resources (although they may sometimes be very high) and thus a fixed budget can be used – but there is one exception, human life, which is considered priceless. However, the figure changes when the budget is not fixed to a certain maximum amount. Replacing a “company” with an “individual,” and the “probability of a major accident scenario” with the “probability of dying,” the coefficient assigning a numerical value per unit of risk can be determined by asking people. The VoL or the value of statistical life (VoSL) is an extremely sensitive and much-debated subject. As the VoSL raises emotive feelings among many people, the concept is also often framed in terms of “the value of a life saved,” “the cost of a fatality averted,” or “the value of preventing a statistical fatality.” Nonetheless, as will become clear, efforts to quantify human life are always accompanied by inconsistencies and ethical concerns.
The value of a human life can be discussed in different ways. Obviously, a life is valued much more than the total worth of the various chemical elements composing a body. Dorman [133] indicates that from the time of Hammurabi (eighteenth century bc), attempts have been made to establish the “value” of lives of different classes of people, primarily for the purposes of punishment. A prince would be worth so many peasants in the harsh calculation of Hammurabian justice. In recent history, the most important reason for setting a value on life stems from the problem of establishing awards in wrongful death judgments. The reasoning goes that it is obviously not enough to demand reimbursement for the direct economic costs of dying (e.g., burial and funeral rites), as this does not cover the opportunity cost, i.e., the income that a deceased person would have earned had they lived on. The justice system therefore gravitated toward a procedure that came to be called the “human capital” approach: calculating the present value of the income stream foregone due to premature death. This approach uses the principle that the value of a person's life increases with earning ability and expected longevity, and decreases with age and the interest rate chosen for discounting. Leonard [134] cites cases dating back to 1916 in which expected future earnings were used to compensate wrongful death. As indicated by Dorman [133], this approach can be contested, as from a social viewpoint and the principle that every life should be equal, it is perverse to value citizens only in their capacity to produce. Moreover, there are many reasons for doubting that a person's income necessarily corresponds to their economic contribution to society.
But how can life then be valued? Economic theorists took up this question in the 1970s and 1980s and devised theoretical models based on the premises of expected utility theory. In particular, these economists were interested in the relationship between an individual's WTP for a reduction of the risk of early death and the extra earnings that reduction would make possible, in order to demonstrate the insufficiency of the human capital approach. The measurements that were used to test the theories were done by a process called “contingent valuation,” i.e., asking people. Indeed, the most straightforward approach to the complex problem of valuing changes in fatal (and non-fatal) risk would appear to be that of simply asking a cross-section of the population to state their own values.
In the case of operational safety, the way that people are asked is very important, as the monetary values that individuals place on a certain issue, and especially if that issue concerns human life, depend on how the question is posed. These are referred to as the “willingness to pay” and “willingness to accept” framing of the questions. The WTP refers to how much someone is prepared to pay to prevent a loss occurring, whereas the WTA refers to how much someone is prepared to accept in compensation for the loss of a benefit. In theory, the WTP value should be identical to the WTA value. In practice, it turns out that the WTA values are invariably higher than the WTP values, when individuals are asked to make preference choices. The key reason for this difference is an individual's preference to gain something rather than to lose something, as the negative impact of a loss is considered to be greater than the positive impact of an equivalent gain (cf. the theory on “loss aversion”; see also Section 4.1.3). Figure 4.24 shows that the values of WTP and WTA increase as the probability of the risk increases (when all factors in the risk calculation formula are kept constant, except for the probability p).

Figure 4.24 Willingness to accept (WTA) and willingness to pay (WTP) (no restrictions to the monetary possibilities imposed).
Figure 4.24 also illustrates that, if there is no maximum amount fixed, as the probability of the risk becomes very substantial it is plausible that no amount of money would be satisfactory. Jones-Lee developed a theory in 1989, improving on Dehez and Drèze [135] and Jones-Lee and Poncelet [136], based on the effect that changes in expected longevity have on the quality (not quantity) of potential life, which therefore sidesteps the confusion between accumulating years and accumulating utility. Jones-Lee's goal was to be able to quantitatively measure the lowest value of a risk increase consistent with an infinite compensation required to induce one to accept it, and the degree of risk aversion of an individual. In this way, it would be possible to construct a quantitative estimate for the required compensation to induce an individual to accept a certain risk increase. However, besides the differences in WTP and WTA values, there are other unique difficulties associated with the necessary measurements for determining the value of human life by asking individuals, such as, for example, in what narrative context such a demand makes sense, and how responses will change from one context (e.g., chemical industry) to another (e.g., cycling). Furthermore, if the probability of death is very low, people tend to assume that the adverse event will occur to someone else rather than to themselves, and their WTP value reflects this view (see also Fuller & Vassie [70]). Individuals' valuations of other people's lives also are likely to be lower than the value people put on their own lives. Valuations of life and people's WTP for improved control measures to prevent future loss of life also invariably increase after serious accidents (even if the probability of occurrence remains exactly the same). Moreover, when asking people, many respondents refuse to make such trade-offs, offering zero bids for risk reduction or saying that no level of compensation will induce them to accept an increase in risk. How does one interpret these refusals? And, as also indicated by Dorman [133], how much credence should be placed in responses to purely hypothetical questions, when respondents can simply throw out numbers with no apparent consequences for themselves and/or others? Finally, it is important to notice that valuations of life often vary between organizations, industrial sectors, and countries. These variations can be related to cultural and religious criteria, a company's ability to pay, the dread fear associated with some types of death, and the economic strength of different countries.
It becomes clear that there is no widely accepted method of measuring the VoL, and there probably never will be. But as it was settled earlier in this section that risk monetization is allowed and defensible, the question remains: how can averted fatalities be considered in decision-making for safety budget allocations in organizations?
In healthcare economics, the quality-adjusted life-year (QALY) is often used when trying to formally assess the value-for-money of a healthcare intervention. The QALY is a widely used measure of the burden of a disease, which includes both the quality and the quantity of life saved. It is based on the number of years of life that would be added by an intervention. Each year of perfect health is assigned the value of 1, down to the value of 0 for death. If extra years would not be lived in full health, for example, if the person were to lose a hand, or be blind, and so on, then the extra life-years are given a value between 0 and 1 to take this into account. There are some important drawbacks of the model, leading to the observation that it is hard, if not impossible, to employ in an organizational context. QALYs are designed for cost–utility analyses, and do not provide information on the valuation of life, for instance. Furthermore, QALYs require utility-independent, risk-neutral, and constant proportional trade-off behavior, all conditions that are hard to meet in organizational contexts. To use QALYs, organizations should also be able to assess the health states of their individual employees for possible safety investments they are able to choose from, which is most probably impossible. If one further considers the fact that perfect health is very hard to define, and that some health states may be worse than death (at least for a number of people), the meaning and usefulness of QALYs may be contested even more.
How can the averting of fatalities then be used to measure preferences for safety budget allocations? Let's return to the WTP attempts to value human life. Notice that WTP studies are used in the remainder of this section, because WTA studies are much less reliable than WTP studies due to the massive number of refusals to accept compensation in WTA studies. Based on a large number of value-to-life WTP surveys, different countries have put forward different values per statistical life, to be used, for example, in societal cost-benefit analyses. Table 4.10 provides some VoSL values found in a small selection of different countries.
Table 4.10 Some “value of statistical life” (VoSL) numbers used in different countries
| Country | VoSL (approximate values) (€ millions) | References |
| Australia | 3.0 | Australian Government [137] |
| The Netherlands | 5.8 | IENM [138] |
| United Kingdom | 2.4 | HSE [139] |
| United States of America | 7.0 | DoT [140, 141] |
All amounts have been recalculated to 2014 euros, for the purposes of easy comparison.
In fact, over recent decades, a large variety of studies have been carried out worldwide to determine the VoSL, and an equally large variety of values have been found. Research by Button [141] indicates that, at the time of the research, the official value of a human life varied between €12 000 and €2.35 million. In the cross-country paper by Miller [142], amounts vary between as low as US $40 000 in Bangladesh to as high as US $8.28 million in Japan (both in 1995 dollars). But Miller also shows minimum and maximum amounts of the VoL for individual countries, diverging substantially. Other studies mention other amounts (see, e.g., Sunstein [143]). Roughly, in current euro values, the amounts from the various studies range between around €50 000 to €25 million, if looked upon from a worldwide perspective. Hence, the variation between lowest and highest VoSLs is characterized by a factor of 500. Although the values are so different, it is possible to find some systematicity in the figures. In fact, Miller [142] shows that across countries, the average VoSL varies almost linearly with income. Hence, the so-called “human capital” approach was refused in part because it simply translated greater worldly success into a higher personal “worth” or value, but now the same results appear in the contingent valuation approach. But this should not be surprising, as any attempt to derive values from consumer demand in the marketplace will attach greater weight to the most affluent consumers. In other words, highly paid workers have a higher perceived VoL.
Nonetheless, the problem of using a VoSL in an organizational context can be solved. To use the VoSL in a company situated in a specific country, it is important to realize that, as already mentioned, the value is a relative one, and not intrinsic. This means that different values may be used by different plants belonging to one and the same organization, but situated in different countries. As the values need to be used in a relative way (to make decisions about budget allocation), all the other monetized risk values also depend on the country where the monetization exercise is carried out. Moreover, depending on the probability of the risk, a different VoSL might need to be employed. This is explained by Sunstein [143]. Instead of saying that “a VoSL value is €5 000 000,” for example, it would be more accurate to say that “for risks of 1/10 000, the median WTP, in the relevant population, is €500.” Or that for risks of 1 in 100 000, the median WTP value is €50. However, it is absolutely not clear whether people's WTP to reduce risks is linear. Suppose that people would be willing to pay €50 to reduce a risk of 10−5. Does it follow from this that people would be willing to pay only €5 to eliminate a risk of 10−6, or that, to eliminate a risk of 10−3, people would be prepared to pay €5000? Not necessarily. As the consequence remains the same (i.e., death), it is necessary to compare probabilities of death with one another to have an idea of how people perceive probabilities; i.e., do people display probability-seeking, -neutral, or -averse behavior? Notice at this point that it was already established that people are consequence-averse. Thus, they are, from a relative point of view, prepared to pay more for higher consequence risks (ceteris paribus). This was also discussed in the section on group risk: multiple fatalities count more than single fatalities (see Section 4.10.2.2).
People are very bad at dealing with probabilities, especially if they are extremely low (so-called type II risks). Nonetheless, if people were asked about their WTP based on explicit probability numbers, it may be assumed that they are rationally prepared to pay more for lowering higher-probability than lowering lower-probability type II risks. If this is the case, the VoSL for a 10−4 risk would have to be higher than the VoSL for a 10−6 risk. In fact, the VoSL figure is mostly used by agencies around the globe for the range of risks between 1 in 10 000 and 1 in 1 000 000. In Europe, for example, if a figure of €6 milion is used (e.g., in the Netherlands), it may be more optimal to use several figures: €8 million for risks of 1 in 10 000; €6 million for risks of 1 in 100 000; and €4 million for risks of 1 in 1 000 000. A minimum and a maximum amount would need to be fixed preferably between the 10−4 risk and the 10−6 risk, so that for risks of 1 in 10 000 000, for example, the VoSL would be €4 million in the Netherlands. In this way, it is possible for an organization to make budget allocation decisions in a relative way, and while using local economic information and taking both the probabilities and the consequences of risks into account.
Ale et al. [107] indicate that in the UK, such an approach, i.e., using a higher VoSL for risks close to the limit of intolerability, has been employed in the past. However, from the more recent amended Railways and Other Guided Transport systems (Safety) Regulations 2006, it seems that this difference is no longer used. Nonetheless, there is no reason – scientific or otherwise – given in favor of or against this approach.
4.11 Safety Investment Decision-making for the Different Types of Risk
4.11.1 Safety Investment Decision-making in the Case of Type I Risks
In the case of type I risks, it is possible to specify a concrete break-even safety point for each individual company. First the degree of safety pertaining to the company should be determined. As this degree of safety is relative to the other companies working in the same industrial sector, a defendable assumption would be that a 50% degree of safety corresponds to the LTIFR in the industrial sector of the country or region where the company is situated and that a maximal degree of safety of (100 − ϵ)% corresponds to a corporate LTIFR of 0. Remember from Section 4.6 that LTI frequency rates are used in the case of type I accidents as lagging indicators, and that the safety measured is thus actually “reactive safety,” so it might also be possible to see the degree of safety as some measure of “un-safety.” Nonetheless, for the sake of simplicity, it is called the “degree of safety.” Figure 4.25 illustrates a linear relationship between the degree of safety of a company and its LTIFR. Other linear relationships are possible and safety managers may thus use a company-specific relationship.

Figure 4.25 Lost time injury frequency rate (LTIFR) of an enterprise in terms of its degree of reactive safety.
The illustrative relation from Figure 4.25 can be set out as follows:
wherein it is assumed that a minimum degree of safety is equal to (0 + ϵ)% (hence ![]() ) and wherein
) and wherein ![]() .
.
The model proposed is designed to help with objective investment decision-making for type I risks. In order to provide management decision-making with an objective input, the model should prove that a safety investment for type I risks, corresponding to the degree of safety pertinent to the enterprise, delivers the benefits expected. To achieve this, each company needs to specify in advance the desired break-even safety target ratio (or “BEST ratio”), defined by dividing the calculated expected hypothetical benefits (using definition (ii) of Section 4.2.4) by the SICs. This procedure resembles existing approaches in companies for determining the cost-effectiveness ratio (see also Chapter 6).
The BEST ratio should depend on the degree of safety determined for the company, in the sense that less safe companies (lower safety degree) are more in need of safety investments, and the SICs may thus, in a relative way, be higher than the expected hypothetical benefits for such low-safety companies, certainly when compared with safer companies (higher safety degree). For example, Table 4.11 can be developed and employed by a company safety manager.
Table 4.11 Illustrative example of break-even safety target (BEST) ratios related to company safety degrees
| Company safety degree for type I risks | Minimum BEST ratio |
| 0–0.25 | 0.2 |
| > 0.25–0.50 | 0.5 |
| > 0.50–0.70 | 1.0 |
| > 0.70–0.90 | 1.5 |
| > 0.90–1.0 | 2.0 |
By using a table such as Table 4.11, an enterprise can facilitate the attaining of its objective of an envisioned degree of company safety related to type I risks. Notice further that the relationship shown in Figure 4.25 does not need to be linear and other choices can be made by a company. Therefore, the overall working approach needs to be well considered in advance.
In order to obtain an objective comparison from a corporate point of view, the condition of achieving the BEST ratio can then be used to specify whether the safety investment is recommended or should be reworked. The model suggested in this section thus provides input for corporate management decision-making on safety investments for type I risks. Following an eventual reformulation of the safety investments as a result of applying the model (e.g., the model results in a ratio lower than the BEST ratio specified in Table 4.11), the economic exercise should be redone.
4.11.2 Safety Investment Decision-making for Type II Risks
In the case of type II risks, it is impossible to use LTIFRs to help decision-making, because they provide no information at all about the number of disasters (i.e., type II accidents) that have happened. Therefore, another approach of dealing with such risks needs to be elaborated and employed.
The technique that can be used, is expounded in the Section 5.7. The approach uses a so-called disproportion factor (DF; see Sections 4.11.2.1 and 8.12) and recommends, based on an organization's evaluation of the numerical value of the DF where the net present value (see Chapter 5) becomes zero, whether or not to invest in a prevention decision for type II risks. Hereafter, it is explained how the DF being considered acceptable/usable by the company can be determined, taking the FN curve (explained in this section) as well as societal concerns (Section 4.11.3) into consideration.
4.11.2.1 Disproportion Factor
Before giving more specifications about the DF, it is important to define the so-called proportion factor (PF), which is a term used to indicate the ratio of the costs to the benefits. The PF can then be compared with the numerical value of the DF in order to determine whether the risk reduction measure is “grossly disproportionate” or not.
If
it means that the safety investment is called “disproportionate” or “grossly disproportionate,” and a further risk reduction would be too costly if compared with the extra benefit gained from the safety investment. Hence, in such cases, it would be recommended not to do the investment.
Concerning the range of values that this factor can take, DF is necessarily greater than 1 because otherwise it would mean a bias against safety (or in favor of “un-safety”). According to Goose [144], the value of the DF is rarely over 10 and should never be higher than 30.
Theoretically, the DF is higher when the risk increases and is infinite when the risk level reaches the intolerable region, meaning in fact that the risk must be reduced no matter the cost.
4.11.2.2 Numerical Estimation of the DF
A scheme of calculation has been suggested by Goose [144], using three intermediate factors, called the “how factors,” which, when multiplied together, give an estimation of the value of the DF. They are referred to as “how bad,” “how risky,” and “how variable.” They are calculated through the use of three values which can be extracted from an FN curve (see Sections 4.10.2.2 and 8.12). These values are as follow:
- 1. the sum of the failure rates, expressed in events per year (
 );
); - 2. the “EV” which is sometimes also called potential loss of life and represents the average number of casualties expected per year;
- 3. the maximum potential fatalities (Nmax), which is the worst-case scenario concerning the number of fatalities for a single event;
- 4. a fourth value can be calculated with the ratio of EV to
 , representing the average number of fatalities per event (Nav).
, representing the average number of fatalities per event (Nav).
It should be noted that this method is based on fatality risk alone and the factors are not fully independent, which introduces non-linear weighting. For example, harm is counted twice in the first two factors.
There are different calculation models developed by Goose [144]. Only the “suggested method” by Goose will be explained further. The approach to calculate the three “how” factors is as follows. The “how bad” factor represents the effect of ![]() , the average number of fatalities per event, on the DF:
, the average number of fatalities per event, on the DF:
The “how risky” factor represents the effect of EV, on the DF:
The “how variable” factor represents the effect of the ratio ![]() on the DF:
on the DF:
The DF is then computed by multiplying the “how” factors and adding 3 (dimensionless) to this product:
4.11.2.3 Hypothetical and Illustrative Example of the Calculation of an FN Curve-based DF
In this example, the goal is to show how an FN curve is plotted and how in practice it is possible to extract the three values necessary to estimate the DF from the curve. A hypothetical example will be used in order to illustrate the subject. Throughout the example, N will represent the estimated number of fatalities in each event and f will represent the frequency of each event. Before beginning, care should be taken that there are not different values of frequency corresponding to the same N. If this were the case, a simple addition for each frequency of the same N would solve this issue.
As explained in Section 4.10.2.2, an FN plot is used to present societal risks and plots the cumulative frequency F as a function of the number of casualties N. F is the sum of frequencies of all events where the outcome is N or higher. Data are recovered from records of historical incidents or from quantitative risk analysis. Conventionally, a log–log plot is used because of the wide range of values for F and N.
Step 1. Plotting the FN Curve
In order to plot an FN curve, the fatalities have to be sorted in decreasing order and therefore Nmax becomes the first input in the table. A possible presentation of the data is shown in Table 4.12 and an example of an FN curve once it has been plotted is shown in Figure 4.26.
Table 4.12 Illustrative example of a data table
| Events | Event frequency f (per year) | Event outcome N (number of fatalities) | Cumulative frequency |
| 1 | 0.000 005 | 13 000 | 0.000 005 |
| 2 | 0.000 1 | 4 600 | 0.000 105 |
| 3 | 0.000 5 | 540 | 0.000 605 |
| 4 | 0.01 | 44 | 0.010 605 |
| 5 | 0.02 | 27 | 0.030 605 |
| 6 | 0.08 | 1 | 0.110 605 |

Figure 4.26 Example of a plotted FN curve.
Step 2. Extraction of Useful Data
The goal at this point is to find the value of ![]() , EV, and Nmax in order to use them to calculate the DF. These data can be derived from Figure 4.26, as illustrated in Figure 4.27.
, EV, and Nmax in order to use them to calculate the DF. These data can be derived from Figure 4.26, as illustrated in Figure 4.27.

Figure 4.27 Useful data in an FN curve.
In Figure 4.27, it is possible to see how to graphically extract the first 2 values ![]() and Nmax. In this case:
and Nmax. In this case: ![]() and
and ![]() , Table 4.12.
, Table 4.12.
The extraction of the EV is more difficult because theoretically it is the frequency-weighted average of the casualties:

with Ni and fi the number of casualties and frequency of each event.
It is possible to see in Table 4.13 how to correctly calculate the EV from a data table. Unfortunately, an FN curve is rarely given with its corresponding data table. However, the EV can also be seen as the area under the curve, which is useful, and the reason stems from the fact that when there is a lot of data available, the following equation is true:
with F(Ni) the cumulative frequency for each event.
Table 4.13 Calculation of expectation value from the data table
| Events | Event frequency f (per year) | Event outcome N (number of fatalities) | Expectation value for each event EV |
| 1 | 0.000 005 | 13 000 | 0.065 |
| 2 | 0.000 1 | 4 600 | 0.46 |
| 3 | 0.000 5 | 540 | 0.27 |
| 4 | 0.01 | 44 | 0.44 |
| 5 | 0.02 | 27 | 0.54 |
| 6 | 0.08 | 1 | 0.08 |
| Sum of the values gives total expection value = 1.855 | |||
Step 3. Calculating the Disproportion Factor
The three options for the DF assessment will be dealt with separately and results will be gathered at the end. Table 4.14 sums up the data which will be used all along the estimation.
Table 4.14 Useful data for estimation
| Cumulative frequency | Expectation value | Nmax | Nav | Nmax/Nav |
| 0.110 605 | 1855 | 13 000 | 17 | 775 |
Therefore:

Hence, (Eq. (2)):
4.11.3 Calculation of the Disproportion Factor, taking Societal Acceptability of Risks into Account
In 1978, Fischhoff et al. [145] described a psychometric study in which it was demonstrated that feelings of dread were the major determinant of public perception and acceptance of risk for a wide range of hazards. A psychometric questionnaire was used in order to correlate nine characteristics of risks, resulting in two main factors. The factor “dread risk” included the following items: perceived lack of control, catasrophic potential, inequitable distribution of risks and benefits, fatal consequences and dread. The “unknown risk” factor consisted of the items observability, experts' and laypeople's knowledge about the risk, delay effect of potential damage (immediacy) and novelty (new-old).
In a study by Huang et al. [146], the goal was to find correlations between public perception of the chemical industry and its acceptance in the matter of risks. Based on a survey administered from 1190 participants, four different factors related to social acceptance were found, each one being subdivided into two sub-factors. The first factor, “knowledge,” consisted of a newness factor and a knowledge factor. The second factor, “benefit,” consisted of the benefit and immediacy together. “Effect” was matched with the third factor and divided between social effect and dread. Finally, “trust” included controllability and trust in governments.
The four factors were then linked with social acceptance through a regression analysis. It is important, however, to specify that knowledge should be understood from the perspective of citizens and that the social effect actually implies “How many citizens are exposed to the risk?” Moreover, the factor “trust in government” also concerns policymakers in a broader sense.
In a study by Gurian [147], the focus was more on how risks are perceived and considered by the general public and society, rather than focusing on the industry's point of view. Based on theoretical explanations, Gurian [147] defined three factors that influence risk perception. The first one, “dread,” included gut-level (related to intuition), the emotional reaction due to risk, threat to future generations, control over the risk, equitability and catastrophic potential. The second factor, “familiarity,” comprised delayed effects, newness, understood by science or not, and encountered often by the public or not. Finally, the last factor was about the “number of people exposed to the risk.”
Adams [148] used the risk thermostat model to describe the perception of risks and, again, a new classification of risks is given depending on three main factors: voluntariness, individual control, and profit-motivated. The acceptability model developed by Adams and resulting from the risk thermostat model is shown in Figure 4.28.

Figure 4.28 Acceptability model developed.
Source: Adams [148]. Reproduced with permissions from Springer.
This study is very similar to those of Gurian [147], Fischhoff et al. [145] and Huang et al. [146], as it focused on the perceived levels of risks to laypeople.
A study by Baker and Dunbar [149] takes societal concerns into account from a risk managers' point of view. The Baker model can be seen as an adaptation of a previous study by Mansfield [150]. Mansfield's more complex model describes a variety of societal concerns in the decision-making process. Baker and Dunbar [149] constructed a systematic framework for the Rail Safety and Standards Board (RSSB), which helped to determine the extent of societal concern in specific cases. They even mentioned that they believe a systematic framework is required so that the factors that have been considered in any facilitated evaluation are completely transparent. However, this model is focused on the transport and rail industry and cannot be used directly for industry in general.
Figure 4.29 shows how the model is structured with the six high-level concern factors. As found in several studies, they use spider diagrams to present the results, which make for an interesting visual representation.

Figure 4.29 Structure of the model developed for the rail industry.
Source: Baker and Dunbar [149]. Reproduced with permission of Rail Safety and Standards Board.)
In a study by Sandman [151], the goal was to develop software that allows a prediction and management solutions to deal with what they call “outrage,” which is closely related to the notion of societal acceptability. Sandman defined risk as the sum of hazard and outrage, with hazard being the standard, well-known term used by risk managers (hazard = magnitude × probability) and outrage being related to the public's perception of risk. The idea is that risk assessors see risk only as hazard, e.g., only with the expected annual mortality, whereas the public sees it as a combination of hazard and outrage. Twelve outrage items are then given and can be described in this case using two words at a time. The first one stands for lower chances of outrage and the second for higher chances of outrage: voluntary versus coerced, natural versus industrial, familiar versus exotic, not memorable versus memorable, not dreaded versus dreaded, chronic versus catastrophic, knowable versus unknowable, controlled by us versus controlled by them, fair versus unfair, morally irrelevant versus morally relevant, trusted versus not trusted, and responsive process versus unresponsive process.
4.11.3.1 Societal Acceptability Indicators with Respect to Disaster-related Risks
In this section, indicators provided in the literature influencing societal acceptability with respect to disaster-related risks are described and a brief comment and description are given for the approach being described. In fact, the indicators mentioned in the literature all play a role when it comes to determining the possible acceptability of a level of risk. They are, however, not always relevant when the focus should be on disaster-related risks, and from the viewpoint of company safety management. The framework of this work is therefore constrained to the industrial sector making risk assessments for major accident prevention. That is why only those indicators concerned with societal acceptability related to major accident risks will be presented, and it will also be explained how these indicators can be organized and grouped together, and finally how they can used in the approach that we describe and propose. In fact, the main goal in this part is also to draw parallels between different indicators used in literature which could refer to the same idea or concept and therefore be merged under the same indicator. The 11 indicators are as follows:
- Indicator no. 1 – Trust in governments, experts, and company (technical community)This indicator reflects the confidence in those responsible for understanding and managing the risks. It is sometimes also seen as “credibility,” meaning that there is regulation and effective enforcement. In the literature, the indicator is mentioned in Mansfield [150], Baker and Dunbar [149], Sandman [151], and Huang et al. [146].
- Indicator no. 2 – Allocation of risks and benefitsThis indicator is concerned with whether there is a fair distribution of benefits for the bearers of risk. It is mentioned in Huang et al. [146] with a discussion about local economic development. The tricky point here is that an industrial activity might always be seen as more beneficial for the company (from the risk bearers' point of view) and therefore might create a bias in the scoring model to be developed in this section. It might also be correlated with profit motivation [148]. In the literature, the indicator is also mentioned in Otway [152], Baker and Dunbar [149], Sandman [151], and Huang et al. [146].
- Indicator no. 3 – History of bad adviceThe indicator concerns the history of the company regarding the given risk and generally if there were recent accidents involving the company itself. The indicator can also be referred to as the history of bad practices. In the literature, it is mentioned in Mansfield [150] and Baker and Dunbar [149].
- Indicator no. 4 – Common-dreadAn indicator such as “common-dread” is rather subjective and it might be possible to group it with personal experience (or difficulties in conceptualizing the risk exposure). The indicator can also be referred to as fear of harm [149], emotional reaction, or gut-level [147]. In the literature, it is mentioned in Fischhoff et al. [145], Mansfield [150], and Sandman [151].
- Indicator no. 5 – Man-made versus natural causesThis indicator is related to whether the accident is due solely to natural causes or whether it is a modern technological catastrophe. For example, an accident caused only by hard-to-predict natural causes may be more accepted than one caused by technical failure. In the literature, it is mentioned in Otway [152], Mansfield [150], Baker and Dunbar [149], and Sandman [151].
- Indicator no. 6 – Scientific knowledgeThis indicator is also referred to as “uncertainties.” It is defined as the experts' knowledge and agreement regarding the considered risk. In the literature, it is mentioned in Fischhoff et al. [145], Otway [152], Mansfield [150], Baker and Dunbar [149], Gurian [147], and Sandman [151].
- Indicator no. 7 – Lack of personal experienceSometimes grouped with personal knowledge, this indicator is also a sensitive and subjective factor. In the literature, it is mentioned in Otway [152], Mansfield [150], and Baker and Dunbar [149].
- Indicator no. 8 – History of the risk itselfThis indicator is related to the history of the hazard itself (for risk bearers), e.g., if there was a recent accident involving the same hazard. It can also be referred to as the frequency of the hazard. In the literature, it is mentioned in Baker and Dunbar [149] and Sandman [151], which describes it as comprising accidents that linger in the public's mind. It is also closely related to personal experience as well as news, fiction symbols and even signals such as an odor.
- Indicator no. 9 – Public's knowledgeThis indicator is also referred to as uncertainties to the risk bearers or accessibility to reliable information (and even difficulties in conceptualizing the risk exposure). It is hard to assess because it is quite subjective. In the literature, it is mentioned in Fischhoff et al. [145], Otway [152], Mansfield [150], Baker and Dunbar [149], Sandman [151], and Huang et al. [146].
- Indicator no. 10 – Environmental/ecological impactIt is difficult to assess how important this indicator is to people, even though environmental issues now raise many more concerns than previously. In the literature, it is mentioned in Mansfield [150] and Baker and Dunbar [149].
- Indicator no. 11 – Lack of personal control over the hazard/situationThis indicator can be seen as the possibility of avoidance thanks to personal skills, for example, or the existence of alternatives for the risk bearers. In the literature, it is mentioned in Fischhoff et al. [145], Otway [152], Baker and Dunbar [149], Adams [148], Sandman [151], and Huang et al. [146].
4.11.3.2 Factor Analysis and Resulting Classifications of Relevant Factors
In order to classify the different indicators, a factor analysis was conducted, the results of which led to the development of the scoring system that follows [153]. The purpose of the study was to examine the factor structure of the societal acceptability of risks (SAR) scale [153]. The first factor consisted of four items (note that the “items” are refereed to as “indicators” in the previous section) and explained 24.73% of variance, the second and third factors each consisted of three items, explaining 11.78% and 10.10% of the variance, respectively, and the fourth factor consisted of only one item that explained 9.61% of the variance. Factor I (four items) consists of items related to the awareness of the company of the risk and fairness of dealing with it; factor II (three items) consists of items related to trust in risk bearers; factor III (three items) consists of items related to the characteristics of the major hazard and its consequences; and factor IV refers to trust in safety management. Figure 4.30 illustrates the results of the confirmatory factor analysis.

Figure 4.30 Second-order factor structure of the societal acceptability of risks.
The factors presented as relevant have therefore been sorted and included into a scoring system which is explained in the following. The classification of each indicator into the main factors (FI, FII, FIII, and FIV) has been done depending on their order of consistency in the factor analysis, but the same weight in the scoring system has been applied in the end due to small differences between them.
4.11.3.3 Scoring System Development
Level of Societal Concern
The model developed in this section is a scoring system that can be filled in directly by safety management, e.g., by board members of a safety committee from the point of view of assessing societal concerns that might arise before or after an accident occurred, and that may thus be important when deciding on safety investments. The idea is therefore to try to picture how workers in a company or outsiders might view the safety management setup in their workplace and what kind of concerns they might have. There are, indeed, cases where the costs due to a strong public reaction were very high. This system therefore identifies, from the perspective of the company managing the hazard, the potential factors influencing this type of situation.
The different factors as listed in the previous section can be grouped into subcategories. Ideally, each subcategory tackles a “key idea” of SAR. As the standard calculation of the DF as proposed by Goose [144] already takes into account the maximum number of casualties (Nmax) and the average number of fatalities per year (EV) and per event (Nav), these factors (which are often described as the severity of consequences) should not be considered again in the model that is being developed. As already explained, the goal of the model is to offer an approach regarding how to include moral aspects in the DF, taking societal acceptance of major hazards into account for the industrial sector in general. It therefore incorporates each relevant factor into a scoring system that gives the global level of concern as an output. Depending on the level of societal concern, the DF is then modified accordingly.
Furthermore, the developed model needs to be designed keeping in mind that it should always possible to use a neutral score for each question. This implies that if one scores between 0 and 4, e.g., 2, this should indicate some kind of neutrality. In this way, it is possible for the user of the scoring system to “skip a question,” e.g., if the indicator seems inappropriate or it does not fit the considered case.
FI (Four Indicators) – “Awareness of Company about the Risk and Fairness of Its Management” (16 Points Maximum)
- FI-1 – History of the risk itself for the risk bearers
The indicator “history of the risk itself for the risk bearers” questions whether there were recent accidents involving the same hazard. (And is it relevant, meaning can people still recall this event?) It can be seen also as previous accidents drawing a lot of media attention or strong protests.
The score that needs to be given by the user of the scoring system for calculating the DF* varies from 0 (which corresponds to hardly any records of accidents of the same type) through 2 (neutral score) to 4 (corresponding to many records of accidents of the same type).
- FI-2 – History of bad advice
The indicator “history of bad advice” is a reflection of whether the company has had a large-scale industrial accident before, which it can be assumed is still in the risk bearers' memory.
The score that needs to be given by the user of the scoring system for calculating the DF* varies from 0 (which corresponds to excellent safety records for the company) through 2 (neutral score) to 4 (corresponding to poor safety records for the company).
- FI-3 – Fair allocation of risks and benefits
The main idea of this indicator “fair distribution of risks and benefits” is to determine whether the risks and benefits are fairly distributed among the risk bearers and the risk beneficiaries. In fact, the aim is to avoid cases of moral hazards when one person is willing to maintain a risky situation because he or she does not bear the consequences and only has the benefits.
The score that needs to be given by the user of the scoring system for calculating the DF* varies from 0 (which corresponds to a fair distribution of risks and benefits) through 2 (neutral score) to 4 (corresponding to an unfair distribution of risks and benefits).
- FI-4 – Common-dread
The indicator “common-dread” questions whether the risk bearers are able to reason in a rational way when facing the hazard/situation. Is it possible that risk bearers have a great sense of dread that would influence their reaction? The idea here is to determine the level of fear of harm or the level of emotional “gut reaction.” It can also be seen as a possibility of dramatization of the risk by the public.
The score that needs to be given by the user of the scoring system for calculating the DF* varies from 0 (corresponding to a hazard that is not very frightening) through 2 (neutral score) to 4 (corresponding to a great sense of dread associated with the considered hazard).
FII (Three Indicators) – “Trust in Risk Bearers” (12 Points Maximum)
- FII-1 – Individual control over the hazard/situation
The indicator “individual control over the hazard/situation” tries to capture the level of personal control over the situation for the person exposed to the risk. It can also be seen as the availability of alternatives when facing the hazard. With this factor, the possible response skills of the risk bearers can be evaluated.
The score that needs to be given by the user of the scoring system for calculating the DF* varies from 0 (which corresponds to total control for the individual) through 2 (neutral score) to 4 (corresponding to no control at all for the individual).
- FII-2 – Lack of personal experience
The indicator “lack of personal experience” verifies whether there is a lack of personal experience among risk bearers for the considered risk. In fact, if risk bearers have personal experience with the risk/situation, the risk is more likely to be accepted.
The score that needs to be given by the user of the scoring system for calculating the DF* varies from 0 (which corresponds to a lot of experience for the individual) over 2 (neutral score) to 4 (corresponding to no experience at all for the individual).
- FII-3 – Uncertainties: public's point of view
The indicator “uncertainties: public”s point of view' can be seen as the public's knowledge of the considered risk, i.e., how much does the public at large, or more specifically the risk bearers, know about the hazard? Is it well known by the public? Can people easily understand this risk? It can also be seen as the accessibility to reliable information.
The score that needs to be given by the user of the scoring system for calculating the DF* varies from 0 (which corresponds to easily known by the public) through 2 (neutral score) to 4 (corresponding to great uncertainty or a complex hazard that is difficult to understand).
FIII (Three indicators) – “Characteristics of the Major Hazard and Its Consequences” (12 Points Maximum)
- FIII-1 – Uncertainties: science point of view
The indicator “uncertainties: science point of view” can be seen as the experts' knowledge and agreement concerning the studied hazard. How much does science know about the risk? Is it well known by the technical community? Do experts agree on how to manage the risk?
The score that needs to be given by the user of the scoring system for calculating the DF* varies from 0 (which corresponds to perfectly known by the technical community) through 2 (neutral score) to 4 (corresponding to great uncertainty or no agreement at all among scientists).
- FIII-2 – Environmental impact
The indicator “environmental impact” assesses whether the hazard could have a (major) environmental impact or not. For example, a chemical leak into a river or a radioactive fallout could have a major impact upon perception of the risk.
The score that needs to be given by the user of the scoring system for calculating the DF* varies from 0 (which corresponds to no environmental impact) through 2 (neutral score) to 4 (corresponding to tremendous environmental impact).
- FIII-3 – Man-made vs natural causes
The main idea of the indicator “man-made versus natural causes” is to determine whether the accident could be caused by human error or natural causes. Human error (score 2) includes, for example, a miscalculation of the resistance of a physical barrier or a mismanagement of the risk. A plane crash as a result of a storm is an example of a neutral score.
The score that needs to be given by the user of the scoring system for calculating the DF* varies from 0 (which corresponds to purely natural causes) through 2 (neutral score) to 4 (corresponding to purely human and/or technical causes).
FIV (One Indicator) – “Trust in Company's Safety Management” (Four Points Maximum)
The indicator “trust in the company” (which in this case is also the factor) indicates to what extent it is believed that the people exposed to the risk (or the citizens most likely to criticize company policies) trust the company's risk management abilities? The main idea of this factor is to take into account the perception of risk bearers regarding the company's safety management.
The score that needs to be given by the user of the scoring system for calculating the DF* varies from 0 (which corresponds to a complete trust in management practices) through 2 (neutral score) to 4 (corresponding to a complete mistrust in management practices).
Effective Use of the Scoring System – Calculation of DF*
Different factors can determine whether or not societal concerns might arise from a situation. A value needs to be assigned to each indicator, so that a value is determined for each factor, eventually providing a corresponding weight factor in the equation to calculate the DF*.
However, suitable ranges of values need to be carefully chosen so that the original DF does not change too much. In fact, the idea is to have slight modifications of the value calculated with the economic model developed by Goose [144]. The estimated level of societal concern (low, neutral, or high) should merely be an indication of the value of the weight factors applied to the DF in order to give the modified DF*. This specific point has been verified by a sensitivity analysis that is described in the next section.
In the following model, the user should bear in mind that the advised range of values given by Goose [144] for the DF remains between 3 and 30 (DF ∈ [3;30]). It is possible to imagine a case where high societal concerns could raise the DF over 30, but that should only happen in very specific cases.
An Excel document can be created for this purpose, containing all the necessary calculations on a unique spreadsheet and therefore allowing direct use of the scoring system. The factor table summarizing the layout for each factor and indicator in the Excel document is presented in Figure 4.31. It is important to point out that the model described in what follows should only be considered as a guidance tool. It should therefore be seen as a suggestion and not as the only possible way to do it.

Figure 4.31 Scoring system for disproportion factor (DF), taking societal acceptability of risks into account: layout of the factors in the Excel file.
A separate spreadsheet can be created with the weight factors that should be applied depending on the total score for each main factor. An example of how the weight factors are chosen is given in Figure 4.32.

Figure 4.32 Example of factor FIII and its corresponding weight factor WFIII.
It should be noted that a choice needs to be made concerning the possible negative impact of this kind of assessment. It has been supposed that social impacts are rarely in favor of a company, especially in industry. That is why it is impossible to reduce in this model the value of the DF with a weight factor lower than 1.
The final step is then to multiply the initial value of the DF by the four weight factors (WFi) as described in the following formula:
Discussion of the Suggested Scoring System
The scoring system described is one that may be used by risk managers so as to include the SAR in economic analyses of industrial risks. It is quite easy to understand and to picture each of the parameters included in the model, and especially how it works as a whole. It is also flexible in the sense that it can be adapted to different situations. Specific parameters can even be chosen as neutral so that they have no impact on the final outcome. Finally, the scoring system is complete in the sense that all the indicators known to be influential for the SAR and relevant within the framework of the prevention of major industrial accidents have been included and weighted according to their importance.
Disadvantages of this model include the subjectivity introduced by the fact that users are free to change some of the parameters and to apply different weight factors depending on the desired sensitivity and the final impact on the DF. Another item of concern is that this model still needs risk managers who are ready to take the leap and include it in economic analyses of their organizations' risks.
The scoring system allows the user to assess the level of societal concerns by identifying situations where public outrage could spill over. It also provides guidance about the main factors influencing societal acceptability along with a means of including it in the previously developed DF model (based solely on the numbers of fatalities and the FN curve) thanks to weight factors. In fact, 11 indicators have been identified, explained and grouped into four main factors.
Regarding further adjustments, it is possible to imagine, for example, the development of actual software with an interface that would make it even more user-friendly and with an extensive database that would allow access to information and good descriptions of the terms or the context. It could provide details about every parameter, but also information on specific cases, and give examples of how to solve certain issues related to this topic (e.g., trust improved with better risk communication, or knowledge of workers increased with awareness campaigns).
4.12 Conclusions
Making decisions generally requires a choice between different alternatives and their possible outcomes. These are frequently associated with risk and uncertainty. The same applies to decisions that companies have to make concerning investments in safety. Not investing in safety entails risk and uncertainty: it can result in loss (in the case of an accident) or in hypothetical gain (if the accident does not occur) [29].
There is no simple recipe for evaluating and managing the risks and uncertainties associated with decision-making [87]. Also, decision-making under uncertainty is not the same as decision-making under risk. Under risk, all outcomes, as well as the likelihood of each outcome, are known. Under uncertainty, some of the alternatives and outcomes, in addition to the likelihood, can be unknown [155]. However, the distinction between risk and uncertainty is not very clear, as risks are very uncertain. After all, likelihoods are only an approximation for predicting uncertain events. So, predictions of risk are characterized by uncertainty [86, 87].
Risk analyses are often used in combination with risk acceptance criteria in order to support the decision-making [86, 88]. Risk acceptance criteria are defined as the upper limits of acceptable risk or tolerable. Based on the risk acceptance criteria, one can decide on the need for risk-reducing measures [88]. The criteria can result from one's own risk appreciation, or they can be legislation-driven or based on corporate guidelines. Defining risk acceptance criteria is, however, difficult. Acceptable risks concerning the safety of assets, personnel, and third parties as external population need to be determined by balancing different concerns [156].
Much debated and complex problems in this regard are the moral aspects of risk, comparison of risks, monetization of risk and, ultimately, the VoSL. These topics have all been discussed in this chapter, and new approaches to deal with them in an organizational context and for the purposes of economic analysis have been suggested.
References
- [1] Shafir, E., Simonson, I., Tversky, A. (1993). Reason-based choice. Cognition, 49, 11–36.
- [2] Aliev, R.A., Huseynov, O.H., Pedrycz, W. (2012). Decision theory with imprecise probabilities. International Journal of Information Technology and Decision Making, 11(2), 271–306.
- [3] Johnson, E.J., Weber, E.U. (2008). Decisions under uncertainty: psychological, economic, and neuroeconomic explanations of risk preference. In: Neuroeconomics: Decision Making and the Brain (eds Glimcher, P., Camerer C., Fehr E. & Poldrack R.) Elsevier, New York, pp. 127–144.
- [4] Kahneman, D., Tversky, A. (1984). Choices, values, and frames. American Psychologist, 39(4), 341–350.
- [5] Levy, J. S. (1992). An introduction to prospect theory. Political Psychology, 13(2) 171–186.
- [6] Hayden, B.Y., Platt, M.L. (2009). The mean, the median, and the St. Petersburg paradox. Judgment Decision Making, 4(4) 256–272.
- [7] Hey, J.D. (2002). Experimental economics and the theory of decision making under risk and uncertainty. The Geneva Papers on Risk and Insurance Theory, 27, 5–21.
- [8] Loewenstein, G., Prelec, D. (1991). Decision making over time and under uncertainty: a common approach. Management Science, 37(7), 770–786.
- [9] Weber, M. (1987). Decision making with incomplete information. European Journal of Operational Research, 28, 44–57.
- [10] Abdellaoui, M., Bleichrodt, H., Paraschiv, C. (2007). Loss aversion under prospect theory: a parameter-free measurement. Management Science, 35(10), 1659–1674.
- [11] Abrams, R.A., Curley, S.P., & Yates, F. (1986). Psychological sources of ambiguity avoidance. Organizational Behavior and Human Decision Processes, 38, 230–256.
- [12] Bassen Jr, A.W. (1987). The St. Petersburg paradox and bounded utility. History of Political Economy, 19(4) 517–523.
- [13] Bell, D.E. (1985). Disappointment in decision making under uncertainty. Operations Research, 33(1) 1–27.
- [14] Borghans, L., Golsteyn, B.H.H., Heckman, J.J., and Meijers, H. (2009) Gender Differences in Risk Aversion and Ambiguity Aversion. IZA Discussion Paper No. 3985.Maastricht University, the Netherlands.
- [15] Cosmides, L., Hell, W., Rode, C., & Tooby, J. (1999). When and why do people avoid unknown probabilities in decision under uncertainty? Testing some predicions from optimal foraging theory. Cognition, 72, 269–304.
- [16] Fox, C.R., Tversky, A. (1998). A belief-based account of decision under uncertainty. Management Science, 44(7) 879–895.
- [17] Gonzalez, R., Wu, G. (1998). Common consequence conditions in decision making under risk. Journal of Risk and Uncertainty, 16, 115–139.
- [18] Gonzales, R., Wu, G. (1999). Nonlinear decision weights in choice under uncertainty. Management Science, 45(1), 74–86.
- [19] Hey, J.D., Lotito, G., Maffioletti, A. (2010). The descriptive and predictive adequacy of theories of decision making under uncertainty/ambiguity. Journal of Risk and Uncertainty, 41, 81–111.
- [20] Tversky, A., Wakker, P. (1995). Risk attitudes and decision weights. Econometrica, 63(6), 1255–1280.
- [21] Cooke, A.D.J., Mellers, B.A., Schwartz, A. (1998). Judgment and decision making. Annual Review of Psychology, 49, 447–477.
- [22] Bleichrodt, H., Pinto, J.L. (2002). Loss aversion and scale compatibility in two-attribute trade-offs. Journal of Mathematical Psychology, 46, 315–337.
- [23] Hsee, C.K., Rottenstreich, Y. (2001). Money, kisses, and electric shocks: on the affective psychology of risk. Psychological Science, 12(3), 185–190.
- [24] Kahneman, D. (1991). Judgment and decision making: a personal view. Psychological Science, 2(3) 142–145.
- [25] Kahneman, D., Lovallo, D. (1993). Timid choices and bold forecasts: a cognitive perspective on risk taking. Management Science, 39(1), 17–31.
- [26] Kahneman, D., Novemsky, N. (2005). The boundaries of loss aversion. Journal of Marketing Research, 42, 119–128.
- [27] Kahneman, D., Tversky, A. (1992). Advances in prospect theory: cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5, 297–323.
- [28] Köbberling, V., Wakker, P.P. (2005). An index of loss aversion. Journal of Economic Theory, 122, 119–131.
- [29] Barkan, R., Erev, I., Zohar, D. (1998). Accidents and decision making under uncertainty: a comparison of four models. Organizational Behavior and Human Decision Processes, 74(2), 118–144.
- [30] Idson, L.C., Higgins, T., Liberman, N. (2000). Distinguishing gains from nonlosses and losses from nongains: a regulatory focus perspective on hedonic intensity. Journal of Experimental Social Psychology, 36, 252–274.
- [31] Wikipedia (English) (2016). Prospect Theory, https://en.wikipedia.org/wiki/Prospect_theory.
- [32] LessWrong (2011) Prospect Theory: a Framework for Understanding Cognitive Biases, http://lesswrong.com/lw/6kf/prospect_theory_a_framework_for_understanding/ (accessed 24 February 2016).
- [33] Ariely, D., Huber, J., Wertenbroch, K. (2005). When do losses loom larger than gains?, Journal of Marketing Research, 42, 134–138.
- [34] Driver-Linn, E., Gilbert, D.T., Kremer, D.A., Wilson, T.D. (2006). Loss aversion is an effective forecasting error. Psychological Science, 17(8), 649–653.
- [35] Gächter, S., Herrmann, A., Johnson, E.J. (2010) individual-level loss aversion in riskless and risky choices. CeDEx Discussion Paper Series. University of Nothingham, Nothingham.
- [36] Kahneman, D., Knetsch, J.L., Thaler, R.H. (1991). Anomalies: the endowment effect, loss aversion, and status quo bias. Journal of Economic Perspectives, 5(1), 193–206.
- [37] Jovanovic, P. (1999). Application of sensitivity analysis in investment project evaluation under uncertainty and risk. International Journal of Project Management, 17(4), 217–222.
- [38] Gollier, C., Treich, N. (2003). Decision-making under scientific uncertainty: the economics of the precautionary principle. The Journal of Risk and Uncertainty, 27(1), 77–103.
- [39] March, J.G., Shapira, Z. (1987). Managerial perspectives on risk and risk taking. Management Science, 33(11) 1404–1418.
- [40] Finuncane, M.L., MacGregor, D.G., Peters, E., Slovic, P. (2004). Risk as analysis and risk as feelings: some thoughts about affect, reason, risk and rationality. Risk Analysis, 24(2) 311–322.
- [41] Finuncane, M.L., MacGregor, D.G., Peters, E., Slovic, P. (2005). Affect, risk, and decision-making. Health Psychology, 24(4) S35–S40.
- [42] Cabanis, M., Herrlich, J., Kircher, T., Klingberg, S., Krug, A., Landsberg, M., Wölwer, W. (2014). Investigation of decision-making under uncertainty in healthy subjects: a multi-centric fMRI study. Behavioural Brain Research, 261 89–96.
- [43] Duncan, R.B. (1972). Characteristics of organizational environments and perceived environmental uncertainty. Administrative Science Quarterly, 17(3) 313-327.
- [44] Durbach, I.N., Stewart, T.J. (2012). Modeling uncertainty in multi-criteria decision analysis. European Journal of Operational Research, 223, 1–14.
- [45] Etner, J., Jeleva, M., Tallon, J. (2012). Decision theory under ambiguity. Journal of Economic Surveys, 26(2), 234–270.
- [46] Hastie, R. (2001). Problems for judgment and decision making. Annual Reviews Psychology, 52, 653–683.
- [47] Ho, T., Huynh, V., Nakamori, Y., Ryoke, M. (2007). Decision making under uncertainty with fuzzy targets. Fuzzy Optimization and Decision Making, 6, 255–278.
- [48] Lipshitz, R., Strauss, O. (1997). Coping with uncertainty: a naturalistic decision-making analysis. Organizational Behavior and Human Decision Processes, 69(2), 149–163.
- [49] Liu, X. (2004). On the methods of decision making under uncertainty with probability information. International Journal of Intelligent Systems, 19, 1217–1238.
- [50] Najjaran, H., Sadiq, R., Tesfamariam, S. (2010). Decision making under uncertainty – an example for seismic risk management. Risk Analysis, 30(1) 78–94.
- [51] Chichilnisky, G. (2000). An axiomatic apprioach to choice under uncertainty with catastrophic risks. Resource and Energy Economics, 22, 221–231.
- [52] Huettel, S.A., McCarthy, G., Song, A.W. (2005). Decisions under uncertainty: probabilistic context influences activation of prefrontal and parietal cortices. The Journal of Neuroscience, 25(13), 3304–3311.
- [53] Troffaes, M.C.M. (2007). Decision making under uncertainty using imprecise probabilities. International Journal of Approximate Reasoning, 45, 17–29.
- [54] Simon, H.A. (1989) Bounded Rationality and Organizational Learning. The Artificial Intelligence and Psychology Project. Technical Report AlP – 107, Carnegie Mellon University, Pittsburgh, PA.
- [55] Eisenhardt, K.M., Zbaracki, M.J. (1992). Strategic decision making. Strategic Management Journal, 13, 17–37.
- [56] Whyte, G. (1993). Escalating commitment in individual and group decision making: a prospect theory approach. Organizational Behavior and Human Decision Processes, 54, 430–455.
- [57] Crisan, L.G., Heilman, R.M., Houser, D. (2010). Emotion regulation and decision making under risk and uncertainty. American Psychological Association, 10(2) 257–265.
- [58] Bechara, A., Naqvi, N., Shiv, B. (2006). The role of emotion in decision making. Current Directions in Psychological Science, 45(5) 260–264.
- [59] Harinck, F., Mersmann, P., Van Beest, I., Van Dijk, E. (2007). When gains loom larger than losses. Psychological Science, 18(12), 1099–1105.
- [60] Weber, E.U. (2006). Experience-based and description-based perceptions of long-term risk: why global warming does not scare us (yet). Climatic Change, 77, 103–120.
- [61] Epstein, S., Pacini, R. (1999). The relation of rational and experiential information processing styles to personality, basic beliefs, and the ratio-bias phenomenon. Journal of Personality and Social Psychology, 76(6) 972–987.
- [62] Dane, E., Pratt, M.G. (2007). Exploring intuition and its role in managerial decision making. Academy of Management Review, 32(1) 33–54.
- [63] Beattie, J., de Vries, N., van der Pligt, J., Zeelenberg, M. (1996). Consequences of regret aversion: effects of expected feedback on risky decision making. Organizational Behavior and Human Decision Processes, 65(2) 148–158.
- [64] Riabacke, A. (2006). Managerial decision making under risk and uncertainty. IAENG International Journal of Computer Science, 32(4) 1–7.
- [65] Donkers, B., Melenberg, B., Van Soest, A. (2001). Estimating risk attitudes using lotteries: a large sample approach, Journal of Risk and Uncertainty, 22(2) 165–195.
- [66] Allman, J.M., Camerer, C.F., Grether, D.M., Kovalchik, S., Plott, C. R. (2005). Aging and decision making: a comparison between neurologically healthy elderly and young individuals. Journal of Economic Behavior & Organization, 58, 79–94.
- [67] Frederick, S. (2005). Cognitive reflection and decision making. Journal of Economic Perspectives, 19(4), 25–42.
- [68] Booth, A.L. and Nolen, P.J. (2009) Gender Differences in Risk Behavior: Does Nurture Matter? IZA Discussion Paper No. 4026. Institute for the Study of Labour, Bonn
- [69] Eckel, C., Grossman, P.J. (2008) Men, women and risk aversion: experimental evidence, Chapter 113, in Handbook of Experimental Economics Results, vol. 1, Part 7.Elsevier, Amsterdam
- [70] Fuller, C.W., Vassie, L.H. (2004). Health and Safety Management. Principles and Best Practice. Prentice Hall, Essex.
- [71] Kletz, T. (1998). Process Plants: A Handbook for Inherently Safer Design. Braun-Brumfield, Ann Arbor, MI.
- [72] Kletz, T., Amyotte, P. (2010). Process Plants. A Handbook for Inherently Safer Design, 2nd edn. CRC Press, Boca Raton, FL.
- [73] Meyer, T., Reniers, G. (2013). Engineering Risk Management. De Gruyter, Berlin.
- [74] Wilson, R., Crouch, E.A.C. (2001). Risk-Benefit Analysis, 2nd edn. Harvard University Press, Newton, MA.
- [75] Busenitz, L.W., Barney, J.B. (1997). Differences between entrepreneurs and managers in large organizations: biases and heuristics in decision-making. Journal of Business Venturing, 12, 9–30.
- [76] Krueger, N. Jr., Dickson, P.R. (1994). How believing in ourselves increases risk taking: perceived self-efficacy and opportunity recognition. Decision Sciences, 25(3), 385–400.
- [77] Riabacke, A. (2006). Managerial decision making under risk and uncertainty. IAENG International Journal of Computer Science, 32, 453–459.
- [78] Panopoulos, G.D., Booth, R.T. (2007). An analysis of the business case for safety: the costs of safety-related failures and the costs of their prevention. Policy and Practice in Health and Safety, 1, 61–73.
- [79] Booth, R.T. (2015) http://www.hastam.co.uk/is-zero-accidents-a-valid-safety-aim-part-2-the-case-in-favour-with-reservations-by-professor-richard-booth/ (accessed 6 February 2016).
- [80] Heinrich H.W. (1950). Industrial Accident Prevention, 3rd edn. McGraw-Hill Book Company, New York.
- [81] Bird, E., Germain, G.L. (1985). Practical Loss Control Leadership, The Conservation of People, Property, Process and Profits. Institute Publishing, Loganville, GA.
- [82] James, B., Fullman, P. (1994). Construction Safety, Security and Loss Prevention, Wiley-Interscience, New York.
- [83] Krause T. R. (2011). New Findings on Serious Injuries and Fatalities. BST (Behavioural Science Technology), Ojai, CA.
- [84] Hopkins, A. (2010), Failure to Learn. The BP Texas City Refinery Disaster. CCH Australia Ltd., Sydney.
- [85] Van Nunen, K., Reniers, G., Ponnet, K., Cozzani, V. (2016). Major accident prevention decision-making: a large-scale survey-based analysis. Safety Science, 88, 242–250.
- [86] Aven, T., Kristensen, V. (2005). Perspectives on risk: review and discussion of the basis for establishing a unified and holistic approach. Reliability Engineering and System Safety, 90, 1–14.
- [87] Klinke, A., Renn, O. (2002). A new approach to risk evaluation and management: risk-based, precaution-based, and discourse-based strategies. Risk Analysis, 22(6), 1071–1094.
- [88] Rodrigues, M.A., Arezes, P., Leão, C.P. (2014). Risk criteria in occupational environments: critical overview and discussion. Procedia – Social and Behavioral Sciences, 109, 257–262.
- [89] Chorus, C.G. (2010). A new model of random regret minimization. European Journal of Transport and Infrastructure Research, 10(2), 181–196.
- [90] Dohmen, T., Falk, A., Huffman, D., Sunde, U., Schupp, J., Wagner, G.G. (2011). Individual risk attitudes: measurement, determinants, and behavioral consequences. Journal of the European Economic Association, 9(3) 522–550.
- [91] Butler, J.V., Guiso, L., Jappelli, T. (2014). The role of intuition and reasoning in driving aversion to risk and ambiguity. Theory and Decision, 77(4) 455–484.
- [92] Stanovich, K.E., West, R.F. (2000) Individual differences in reasoning: implications for the rationality debate? Behavioral and Brain Sciences, 23 645–665.
- [93] Klein, G. (1998) Sources of Power: How People Make Decisions. MIT Press, Cambridge, MA.
- [94] Klein, G. (2003) Intuition at Work: Why Developing Your Gut Instincts Will Make You Better at What You Do. Doubleday, New York.
- [95] Dijksterhuis, A. (2004). Think different: the merits of unconscious thought in preference development and decision making. Journal of Personality and Social Psychology, 87(5) 586–598.
- [96] Lee, L., Amir, O., Ariely, D. (2009). In search of Homo economicus: cognitive noise and the role of emotion in preference consistency. Journal of Consumer Research, 36, 173–187.
- [97] Zuckerman, M., Kuhlman, D.M. (2000). Personality and risk taking: common biosocial factors. Journal of Personality, 68, 999–1029.
- [98] Rolison, M.R., Scherman, A. (2003). College student risk-taking from three perspectives. Adolescence 38, 689–704.
- [99] Boyer, T.W. (2006). The development of risk-taking: a multiperspective review. Developmental Review 26, 291–345.
- [100] Ponnet, K., Reniers, G., Kempeneers, A. (2015). The association between students' characteristics and their reading and following safety instructions. Safety Science, 71, 56–60.
- [101] Lang, S. (1973). Calculus of Several Variables. Addison-Wesley, Reading, MA.
- [102] Simon, C. P., Blume, L.E. (1994). Mathematics for Economists. W.W. Norton and Company, New York.
- [103] Adams, J.G.U. (1995). Risk. UCL Press, London.
- [104] Slovic, P. (Ed.) (2000). The Perception of Risk. Earthscan, Virginia.
- [105] Fife, I., Machin, E.A. (1976). Redgrave's Health and Safety in Factories. Butterworth, London.
- [106] Melnick, E.L., Everitt, B.S. (2008). Encyclopedia of Quantitative Risk Analysis and Assessment. John Wiley & Sons, Ltd, Chichester.
- [107] Ale, B.J.M., Hartford, D.N.D., Slater, D. (2015). ALARP and CBA all in the same game. Safety Science, 76, 90–100.
- [108] Ale, B.J.M. (2009). Risk: An Introduction. The Concepts of Risk, Danger and Chance. Routledge, Abingdon.
- [109] Duffey, R.B., Saull, J.W. (2008). Managing Risk: the Human Element. John Wiley & Sons, Ltd, Chichester.
- [110] Ball, D.J. and Floyd, P.J. (1998) Societal Risks. Final Report. HSE, London.
- [111] Reniers, G., Ale, B., Dullaert, W., Foubert, B. (2006). Decision support systems for major accident prevention in the chemical process industry: a developers' survey. Journal of Loss Prevention in the Process Industries, 19, 604–662.
- [112] Sunstein, C.R. (2002). Risk and Reason. Safety, Law and the Environment. Cambridge University Press, Cambridge.
- [113] Evans, A.W., Verlander, N.Q. (1993). What is wrong with criterion FN-lines for judging the tolerability of risk? Risk Analysis, 17(2) 157–168.
- [114] Bedford, T. (2013). Decision-making for group risk reduction: dealing with epistemic uncertainty, Risk Analysis, 33(10), 1884–1898.
- [115] Tweeddale, M. (2003). Managing Risk and Reliability of Process Plants. Gulf Professional Publishing (Elsevier Science), Burlington, MA.
- [116] van Danzig, D. (1956). Economic decision problems for flood prevention, Econometrica, 24, 276–287,
- [117] Jonkman, S.N., Vrijling, J.K., van Gelder, P.H.A.J.M., Arends, B. (2003). Evaluation of tunnel safety and cost effectiveness of measures. Safety and Reliability 2003, Proceedings of ESREL 2003, Swets and Zeitlinger, Lisse.
- [118] van de Poel, I., Fahlquist, J.N. (2013). Risk and responsibility. In: Essentials of Risk Theory (eds Roeser, S., Hillerbrand, R., Sandin, P. & Peterson, M.). Springer, Dordrecht.
- [119] Roeser, S. (2006). The role of emotions in the moral acceptability of risk. Safety Science, 44, 689–700.
- [120] Roeser, S. (2007). Ethical intuitions about risks. Safety Science Monitor, 11(3) 1–13.
- [121] Sunstein, C.R. (2005). Laws of Fear. Beyond the Precautionary Principle. Cambridge University Press, Cambridge.
- [122] Slovic, P. (2002). The affect heuristic. In: Heuristics and Biases: the Psychology of Intuitive Judgment (eds Gilovitch, T., Griffin, D., & Kahneman, D.), Cambridge University Press, Cambridge.
- [123] Wilde, G. (1976). The risk compensation theory of accident causation and its practical consequences for accident prevention. Paper Presented at the Annual Meeting of the Österreichische Gesellschaft für Unfallchirurgies, Salzburg, Austria.
- [124] Adams, J.G.U. (1985). Risk and Freedom: the Record of Road Safety Regulation. Transport Publishing Projects, London.
- [125] Adams, J.G.U. (1988). Risk homeostasis and the purpose of safety regulation, Ergonomics, 31(4) 407–428.
- [126] Kunreuther, H. (1992). A conceptual framework for managing low-probability events. In: Social Theories of Risk (eds Krimsky, S. & Golding, D.), Praeger, London.
- [127] Harris, C.E., Pritchard, M.S., Rabins, M.J. (2008). Engineering Ethics. Concepts and Cases, 4th edn. Wadsworth, Belmont, CA.
- [128] Asveld, L., Roeser, S. (eds) (2009). The Ethics of Technological Risk. Earthscan, London.
- [129] Hansson, S.O. (2009). Risk and safety in technology. In: Handbook of the Philosophy of Science (ed. Meijers, A.). Philosophy of Technology and Engineering Sciences, vol. 9. Elsevier, Oxford, pp. 1069–1102.
- [130] Van de Poel, I., Royakkers, L. (2011). Ethics, Technology and Engineering. Wiley-Blackwell, London.
- [131] Rayner, S. (1992). Cultural theory and risk analysis. In: Social Theories of Risk (ed. Krimsky, G.). Praeger, London.
- [132] Kelman, S. (1981). What Price Incentives? Economists and the Environment. Auburn House Publishing Company, Boston, MA.
- [133] Dorman, P. (2009). Markets and Mortality. Economics, Dangerous Work, and the Value of Human Life. Cambridge University Press, Cambridge.
- [134] Leonard, N. (1969). Future economic value in wrongful death litigation. Ohio State Law Journal, 30, 502–514.
- [135] Dehez, P., Drèze, J. (1982). State-dependent utility, the demand for insurance and the value of safety. In: The Value of Life and Safety: Proceedings of a Conference held by the “Geneva Association” (ed. Jones-Lee M.W.). North-Holland, Amsterdam.
- [136] Jones-Lee, M.W., Poncelet, A.M. (1982). The value of marginal and non-marginal multiperiod variations in physical risk. In: The Value of Life and Safety: Proceedings of a Conference held by the “Geneva Association” (ed. Jones-Lee M.W.). North-Holland, Amsterdam.
- [137] Australian Government, Department of Prime Minister and Cabinet (December 2014) Best Practice Regulation Guidance Note – Value of Statistical Life.
- [138] IENM (2013) Letter of 26 April 2013 to the Parliament, Ministerie van Infrastructuur IENM/BSK 2013/19920.
- [139] HSE (2001) Reducing Risk, Protecting People. Her Majesty's Stationery Office, Norwich NR3 1BQ, p. 36.
- [140] DoT (2013) Guidance on Treatment of the Economic Value of a Statistical Life in U.S. department of Transportation Analysis. Department of Transportation, United States. Memorandum to secretarial officers and modal administrators.
- [141] Button, K. (1993) Overview of Internalizing the Social Costs of Transport. OECD ECMT Report.
- [142] Miller, T.R. (2000). Variations between countries in values of statistical life. Journal of Transport Economics and Policy, 34(2) 169–188.
- [143] Sunstein, C.R. (2013) The Value of a Statistical Life: Some Clarifications and Puzzles. Regulatory Policy Program, RPP-2013-18.
- [144] Goose, M. (2006). Gross Disproportion, Step by Step – A Possible Approach to Evaluating Additional Measures at COMAH Sites. In: Institution of Chemical Engineers Symposium Series, vol. 151, p. 952. Institution of Chemical Engineers, Rugby.
- [145] Fischhoff, B,, Slovic, P., Lichtenstein, S. (1978), How Safe is Safe Enough? A Psychometric Study of Attitudes Towards Technological Risks and Benefits, Elsevier, Amsterdam.
- [146] Huang, L., Ban, J., Sun, K., Han, Y., Yuan, Z., Bi, J. (2013). The influence of public perception on risk acceptance of the chemical industry and the assistance for risk communication. Safety Science 51, 232–240.
- [147] Gurian, P.L. (2008). Risk Perception, Risk Communication, and Risk Management. Drexel University Libraries.
- [148] Adams, J. (2009). Risk management: the economics and morality of safety revisited, In: Safety-Critical Systems: Problems, Process and Practice. Springer, Berlin.
- [149] Baker, E., Dunbar, I. (2004) Modelling Societal Concern for the Rail Industry. Research Programme for the RSSB (Rail Safety & Standards Board).
- [150] Mansfield D (2003) Gauging societal concerns, Symposium Series, vol. 149, In: Hazard XVII: Process Safety – Fulfilling Our Responsibilities, pp. 15–29, IChemE, London.
- [151] Sandman, P.M. (2012) Responding to Community Outrage: Strategies for Effective Risk Communication.[First published in 1993 by the American Industrial Hygiene Association, copyright transferred to the author, Peter M. Sandman, in 2012.]
- [152] Ottway, H.J. (1982), Beyond Acceptable Risk: On the Social Acceptability of Technologies. Elsevier, Amsterdam.
- [153] Achille, J., Ponnet, K., Reniers, G. (2015) Calculation of an adjusted disproportion factor (DF*) which takes the societal acceptability of risks into account. Safety Science DOI: 10.1016/j.ssci.2015.12.007, In Press.
- [154] Quinn, D.J., Davies, P.A. (2004) Development of an Intermediate Societal Risk Methodology. HSE Books, Research Report RR283. HSE, London, http://www.hse.gov.uk/research/rrhtm/rr283.htm (accessed 24 February 2016).
- [155] Mousavi, S., Gigerenzer, G. (2014). Risk, uncertainty, and heuristics. Journal of Business Research, 67 1671–1678.
- [156] Abrahamsen, E.B., Aven, T. (2008). On the consistency of risk acceptance criteria with normative theories for decision-making. Reliability Engineering and System Safety, 93 1906–1910.
