Chapter 7
Beyond the State-of the Art of Operational Safety Economics: Bayesian Decision Theory
7.1 Introduction
The Bayesian decision theory, which is presented in this book as a novel contribution to the decision theoretical field, is a neo-Bernoullian utility theory which also aims to improve on expected utility theory, as did game theory and prospect theory before it. But in its approach it takes the middle road, just as Daniel Bernoulli himself did when he wrote his St. Petersburg paper (see also Chapter 4), in that it recognizes both the desirability of mathematical first principles as well as the necessity for any mathematical theory of human rationality to be able to stand to the benchmark of “common sense.”
The structure of this chapter on the Bayesian decision is as follows. First a theoretical discussion of the Bayesian decision theory is given. Thereafter, the alternative criterion of choice which is proposed in the Bayesian decision theory is used to discuss and explain why type II events are perceived to be more risky than type I events.
In this section, a theoretical discussion of the Bayesian decision theory is given. This is done by relating the Bayesian decision theory to the expected outcome and expected utility theories that came before it. Expected outcome theory has been around since the seventeenth century, when the rich merchants of Amsterdam bought and sold expectations as if they were tangible goods. As already expounded in this book, the algorithmic steps of expected outcome theory are very simple:
- 1. For each possible decision: construct an outcome probability distribution; i.e., for each possible decision, assign to every conceivable contingency both an estimated net monetary consequence and a probability.
- 2. Choose that decision which maximizes the expectation values (i.e., means) of the outcome probability distributions.
In the eighteenth century, Bernoulli provided a fundamental contribution to expected outcome theory in that he proposed that it was not the actual gains and losses that move us, but rather that the utility of these gains and losses. Moreover, Bernoulli offered up a specific function by which to translate these gains and losses to their corresponding utilities:
where ![]() is some scaling constant that falls away in the decision theoretical (in)equalities,
is some scaling constant that falls away in the decision theoretical (in)equalities, ![]() is the initial wealth of the decision-maker, and
is the initial wealth of the decision-maker, and ![]() is either a gain or a loss.
is either a gain or a loss.
In the utility function (Eq. 7.1), the initial wealth functions as a reference point in the following sense. For increments ![]() which are small relative to the initial wealth
which are small relative to the initial wealth ![]() , the utility function (Eq. 7.1) becomes linear, as losses are weighted the same as corresponding gains, whereas for increments
, the utility function (Eq. 7.1) becomes linear, as losses are weighted the same as corresponding gains, whereas for increments ![]() which are large relative to the initial wealth
which are large relative to the initial wealth ![]() , the utility function (Eq. 7.1) becomes non-linear, as losses are weighted more heavily than corresponding gains. So, Bernoulli's utility function predicts that the psychological phenomenon of loss aversion will hold for large consequences such as, say, the burning down of a house, but not for small consequences such as the breaking of an egg. This is commensurate with intuition. Bernoulli, having provided both the concept and the quantification of utilities, proposed his expected utility theory as a straightforward generalization of the expected outcome theory. The algorithmic steps of expected utility theory are as follows [1]:
, the utility function (Eq. 7.1) becomes non-linear, as losses are weighted more heavily than corresponding gains. So, Bernoulli's utility function predicts that the psychological phenomenon of loss aversion will hold for large consequences such as, say, the burning down of a house, but not for small consequences such as the breaking of an egg. This is commensurate with intuition. Bernoulli, having provided both the concept and the quantification of utilities, proposed his expected utility theory as a straightforward generalization of the expected outcome theory. The algorithmic steps of expected utility theory are as follows [1]:
- 1. For each possible decision: construct an outcome probability distribution; i.e, for each possible decision, assign to every conceivable contingency both an estimated net monetary consequence and a probability.
- 2. Transform outcome probability distributions to their corresponding utility probability distributions; i.e., convert the outcomes of the outcome probability distributions to their corresponding utilities, using Bernoulli's utility function.
- 3. Choose that decision which maximizes the expectation values (i.e., means) of the utility probability distributions.
Bernoulli's utility concept remained uncontested in the centuries that followed his 1738 paper, but the same cannot be said for his utility function (Eq. 7.1). Nonetheless, Bernoulli's utility function has been demonstrated also to hold for sensory stimuli perception [2], and not only for monetary stimulus perception. Moreover, Bernoulli's utility function may be derived from sound first principles [1, 3].
In von Neumann and Morgenstern's [4] reintroduction of Bernoulli's expected utility theory, the specific form of the utility function was left unspecified. This added degree of freedom in the expected utility theory opened the way for alternative utility functions such as, for example, the following utility function:
This alternative function (Eq. 7.2), however, does not, like Bernoulli's utility function (Eq. 7.1), have an explicit reference point by which to modulate the strength of the loss aversion effect as a function of both the current asset position and the increment in that asset position. Moreover, Eq. (7.2) lacks the general validity that Eq. (7.1) enjoys as the psycho-physical Fechner–Weber law that guides our human sense perception [2]. Finally, Bernoulli's utility function admits a consistency derivation which shows that the only consistent utility function is either the utility function (Eq. 7.1) or some transformation thereof [3], and it may be shown that Eq. (7.2) does not belong to this class of consistent utility functions. Note that a power function like Eq. (7.2) is found in Eq. (2.2). But there it is not so much an utility transformation, as it is a correction that will ensure a higher modeled risk for type II risks (see also Section 7.5).
7.2 Bayesian Decision Theory
The Bayesian decision theory is “neo-Bernoullian” in that it proposes that the utility function Eq. (7.1) is the most appropriate function by which to translate, for a given initial wealth, gains and losses to their corresponding utilities. But it deviates from both the expected outcome theory and the expected utility theory in that it questions the appropriateness of the criterion of choice where one has to choose the decision that maximizes the expectation values or, equivalently, the means of the outcome probability distributions under the different decisions.
7.2.1 The Criterion of Choice as a Degree of Freedom
Let ![]() and
and ![]() be two actions we have to choose from. Let
be two actions we have to choose from. Let ![]() , for
, for ![]() , and
, and ![]() , for
, for ![]() , be the monetary outcomes associated with, respectively, actions
, be the monetary outcomes associated with, respectively, actions ![]() and
and ![]() . Then in the Bayesian decision theory – as in both expected outcome theory and utility theory – the two outcome distributions that correspond with these decisions are constructed:
. Then in the Bayesian decision theory – as in both expected outcome theory and utility theory – the two outcome distributions that correspond with these decisions are constructed:
One then proceeds – as in expected utility theory – to map utilities to the monetary outcomes in Eq. (7.4), by way of the Bernoulli utility function (Eq. 7.1). This leaves us with the utility probability distributions:
Now, the most primitive intuition regarding the utility probability distributions (Eq. 7.4) is that the action which corresponds with the utility probability distribution lying more to the right (i.e., providing the highest utility of both actions) will also be the action that promises to be the most advantageous. So, when making a decision, we ought to compare the positions of the utility probability distributions on the utility axis and then choose that action which maximizes the position of these utility probability distributions. This all sounds intuitive enough. But how is the position of a probability distribution defined?
Ideally there would be some formal (consistency) derivation of what constitutes a position measure of a probability distribution. But in the absence of such a derivation, ad hoc common-sense considerations need to be used. Stated differently, the criterion of choice in the decision theory constitutes a degree of freedom.
7.2.1.1 The Probabilistic “Worst Case,” “Most Likely Case,” and “Best Case” Scenarios
From the introduction of expected outcome theory in the seventeenth century and expected utility theory in the eighteenth century, the implicit assumption has been that the expectation value of a given probability distribution is a position of its measure [1, 5]. The expectation value is a measure for the location of the center of mass of a given probability distribution; as such it may give one a probabilistic indication of the most likely scenario:
The qualifier “probabilistic indication” is used here to point to the fact that the expectation value or, equivalently, the mean need not give a value that one would necessarily expect.
In the Value at Risk (VaR) methodology used in the financial industry (see also Section 3.4.2) the probabilistic worst-case scenarios are taken as a criterion of choice, rather than the most likely scenarios (in the probabilistic sense). In the VaR methodology the probabilistic worst-case scenario is operationalized as the 1 (or up to 5%) percentile. But instead of percentiles, one may also use the confidence lower bound to operationalize a probabilistic worst-case scenario.
The absolute worst-case scenario is:
The criterion of choice in Eq. (7.6) is also known as the minimax criterion of choice [6]. The k-sigma lower bound of a given probability distribution is given as
where ![]() is the sigma level of the lower bound and where
is the sigma level of the lower bound and where
is the standard deviation. The probabilistic worst case scenario then may be quantified as an undershoot-corrected lower bound (Eqs. 7.6 and 7.7):
Note that the probabilistic worst-case scenario (Eq. 7.9) holds the minimax criterion of choice (Eq. 7.6), as a special case for large ![]() in Eq. (7.7). For
in Eq. (7.7). For ![]() , the criterion of choice (Eq. 7.9) constitutes a still likely worst-case scenario (in the probabilistic sense).
, the criterion of choice (Eq. 7.9) constitutes a still likely worst-case scenario (in the probabilistic sense).
One may also imagine – in principle – a decision problem in which one is only interested in the probabilistic best-case scenarios. The absolute best-case scenario is:
The criterion of choice in Eq. (7.10) is also known as the maximax criterion of choice. The k-sigma upper bound of a given probability distribution is a given as:
where ![]() is the sigma level of the upper bound. The probabilistic best-case scenario may then be quantified as an overshoot-corrected upper bound (Eqs. 7.10 and 7.11):
is the sigma level of the upper bound. The probabilistic best-case scenario may then be quantified as an overshoot-corrected upper bound (Eqs. 7.10 and 7.11):
Note that the probabilistic best-case scenario (Eq. 7.12) holds the maximax criterion of choice, Eq. (7.10), as a special case for large ![]() in Eq. (7.11). For
in Eq. (7.11). For ![]() , the criterion of choice Eq. (7.12) constitutes a still likely best-case scenario (in the probabilistic sense).
, the criterion of choice Eq. (7.12) constitutes a still likely best-case scenario (in the probabilistic sense).
If a criterion of choice as in Eq. (7.5) is considered, then one neglects what may happen in the worst and the best of possible scenarios. If a criterion of choice as in Eq. (7.9) is taken, then one neglects what may happen in the most likely and the best of possible scenarios. If one takes as a criterion of choice Eq. (7.12), then one neglects what might happen in the worst and the most likely of possible scenarios. An exclusive commitment to any of the criteria of choice (Eqs. 7.9, and 7.12), will thus necessarily leave out some pertinent information in one's decision theoretical considerations. So, how does one untie this Gordian knot?
7.2.1.2 A Probabilistic Hurwitz Criterion of Choice
In Hurwitz's criterion of choice, the absolute worst- and best-case scenarios are both taken into account; for a balanced pessimism coefficient of ![]() we have that (Eqs. 7.6 and 7.10):
we have that (Eqs. 7.6 and 7.10):
Now, the absolute worst- and best-case scenarios are replaced in Eq. (7.13) with their corresponding probabilistic undershoot- and overshoot-corrected counterparts (Eqs. 7.9 and 7.12):
Under the criterion of choice in Eq. (7.14), undecidedness between ![]() and
and ![]() translates to the decision theoretical equality:
translates to the decision theoretical equality:
or, equivalently,
a trade-off between the losses/gains in the probabilistic worst-case scenarios (Eq. 7.9), and the corresponding gains/losses in the probabilistic best-case scenarios (Eq. 7.10). It follows, seeing that Eq. (7.13) is a limit case of Eq. (7.14), that for a balanced pessimism coefficient of ![]() Hurwitz's criterion of choice provides a balanced trade-off between the differences in the absolute worst case scenarios and the differences in the absolute best case scenarios.
Hurwitz's criterion of choice provides a balanced trade-off between the differences in the absolute worst case scenarios and the differences in the absolute best case scenarios.
The probabilistic Hurwitz criterion of choice (Eq. 7.14) translates to Eqs. (7.9 and 7.12):
It follows that the alternative criterion of choice (Eq. 7.14), which takes into account what may happen in the worst and the best of possible scenarios, holds both the traditional expected value criterion of choice (Eq. 7.5) as a special case as well as Hurwitz's criterion of choice with a balanced pessimism factor (Eq. 7.13). However, it may be found that the criterion of choice in Eq. (7.14) – and by implication also the Hurwitz criterion of choice (Eq. 7.13) – is vulnerable to a simple counter-example.
Imagine two utility probability distributions having equal lower and upper bounds ![]() and
and ![]() , but one distribution being right-skewed and the other being left-skewed. Then the criterion of choice in Eq. (7.14) will leave its user undecided between the two decisions, whereas intuition would give preference to the decision corresponding with the left-skewed outcome probability distribution, as the bulk of the probability distribution of the left-skewed distribution will be more to the right than that of the right-skewed distribution.
, but one distribution being right-skewed and the other being left-skewed. Then the criterion of choice in Eq. (7.14) will leave its user undecided between the two decisions, whereas intuition would give preference to the decision corresponding with the left-skewed outcome probability distribution, as the bulk of the probability distribution of the left-skewed distribution will be more to the right than that of the right-skewed distribution.
7.2.2 The Proposed Criterion of Choice
The probabilistic Hurwitz criterion of choice (Eq. 7.17) is an alternative to the expectation criterion of choice (Eq. 7.5) , which also takes into account the standard deviation of a given probability distribution, by way of the positions of the under- and overshoot-corrected lower and upper bounds (Eqs. 7.9 and 7.12). But the universality of this proposal is compromised by way of the simple counter-example of a right-skewed and a left-skewed distribution that have the same lower and upper bounds. It follows that a criterion of choice, in order to be universal, should not only take into account the trade-off between the probabilistic worst- and best-case scenarios, as is done in Eq. (7.17), but also the location of the probabilistic bulk of the probability distribution.
The following position measure for a probability distribution accommodates the intuitive preference for the left-skewed distribution of the counter-example, while taking into account the probabilistic worst and best cases:
Note that the alternative criterion of choice (Eq. 7.18), which takes into account what may happen in the worst, the most likely, and the best of possible scenarios, holds the traditional expected value criterion of choice (Eq. 7.5), as a special case.
In any problem of choice, one will endeavor to choose that action which has a corresponding utility probability distribution that is lying most to the right on the utility axis; i.e., one will choose to maximize the utility probability distributions. In this there is little freedom. But one is, of course, free to choose the measures of the positions of the utility probability distributions any way one sees fit. Nonetheless, it is held to be self-evident that it is always a good policy to take into account all the pertinent information at hand.
First, if only the expectation values of the utility probability distributions are maximized, then, by definition, the information that the standard deviations of the utility probability distributions bring to bear on the problem of choice at hand will be neglected.
Second, if only one of the confidence bounds of the utility probability distributions is maximized, while neglecting the other, then a probabilistic minimax or maximax analysis will be performed, and, consequently, the possibility of either the (catastrophic) losses in the lower bound or the (astronomical) gains in the upper bound will be neglected.
Third, if only the sum of the lower and upper bounds are maximized, or a scalar multiple thereof, then a trade-off between the probabilistic worst- and best-case scenarios is made. But in the process, one will, for unimodal distributions, be neglecting the location of the bulk of the probability distributions.
In light of the these three considerations, the scalar multiple, the sum of the undershoot-corrected lower bound, expectation value, and overshoot-corrected upper bound, i.e., Eq. (7.18), is currently believed to be the most all-round position measure for a given probability distribution, as it takes into account the position of the probabilistic worst- and best-case scenarios (Eqs. 7.9 and 7.12), as well as the position of the probabilistic most likely scenario (Eq. 7.5).
7.2.3 The Algorithmic Steps of the Bayesian Decision Theory
The algorithmic steps of the Bayesian decision theory are as follows (van Erp et al. [3]):
- 1. For each possible decision, construct an outcome probability distribution; i.e. for each possible decision, assign to every conceivable contingency both an estimated net monetary consequence and a probability.
- 2. Transform outcome probability distributions to their corresponding utility probability distributions; i.e., convert the outcomes of the outcome probability distributions to their corresponding utilities, using Bernoulli's utility function.
- 3. Maximize a scalar multiple of the sum of the lower bound, the expectation value, and the upper bound of the utility probability distributions; i.e., the criterion of choice in Eq. (7.18).
Note that the Bayesian decision theory is just Bernoulli's expected utility theory, except for the alternative criterion of choice (Eq. 7.18), which is to be maximized. But in the case that the k-sigma confidence lower bound (Eq. 7.7) does not undershoot the absolute minimum (Eq. 7.6), and the confidence upper bound (Eq. 7.11) does not overshoot the absolute maximum (Eq. 7.10), then the criterion of choice (Eq. 7.18) collapses to the expectation value (Eq. 7.5) and, as a consequence, the Bayesian decision theory becomes equivalent to Bernoulli's expected utility theory [1].
7.3 The Allais Paradox
Allais constructed his famous paradox in order to demonstrate the very profound psychological reality of the preference for security in the neighborhood of certainty [7]. For example, if one has to choose between the following two options:
- 1A. 10% chance of winning €100 million and 90% chance of winning nothing;
- 1B. 9% chance of winning €500 million and 91% chance of winning nothing,
then most of us – in correspondence with expected utility theory – will prefer option 1B, which has the greater expected utility. However, if one has to choose between the two options:
- 2A. absolute certainty of winning €100 million;
- 2B. 90% chance of winning €500 million and 10% chance of winning nothing,
then most of us would prefer the secure option 2A, even though the uncertain option 2B has the greater expected utility, providing one is not a multi-billionaire, as we opt for security in the neighborhood of certainty.
Allais offered up his paradox because he felt that the exclusive focus of the expected utility theory on the means (i.e., expectation values) of the utility probability distributions neglects the spread of the probabilities of the utility values around their mean, a spread which – according to Allais – represented the fundamental psychological element of the theory of risk [7].
7.3.1 The Choosing of Option 1B
The outcome probability distributions of the options of the first bet are:

and
The corresponding utility probability distributions, for a monthly initial asset position of, say, ![]() for groceries and the like, are (Eq. 7.1):
for groceries and the like, are (Eq. 7.1):
and
The expected utilities of Eqs. (7.21) and (7.22) are, respectively (Eq. 7.5):
It can be seen in Eq. (7.23) that the expected utility solution of the first bet – for any ![]() > 0 – points to option 1B as the predicted preferred choice.
> 0 – points to option 1B as the predicted preferred choice.
The standard deviations of Eqs. (7.21) and (7.22) are, respectively (Eq. 7.8):
It follows from Eqs. (7.23) and (7.24) that the ![]() sigma confidence intervals (Eqs. 7.7 and 7.11), of the utility probability distributions (Eqs. 7.20 and 7.21) are, respectively:
sigma confidence intervals (Eqs. 7.7 and 7.11), of the utility probability distributions (Eqs. 7.20 and 7.21) are, respectively:
and
The absolute minimal and maximal values (Eqs. 7.6 and 7.10) of the utility probability distributions (Eqs. 7.20 and 7.21) are, respectively:
and
Comparing Eqs. (7.25)(7.26)(7.27), one sees that for the utility probability distribution Eq. (7.21) there occurs a lower bound undershoot, and the same can be seen for the utility probability distribution Eq. (7.22), when one compares Eqs. (7.26)(7.27)(7.28). It follows that for both options of the first bet, the appropriate criterion of choice is the second row of Eq. (7.18):
where ![]() . Substituting Eqs. (7.23), (7.24), (7.27), and (7.28) into Eq. (7.29), we obtain the alternative criteria of choice:
. Substituting Eqs. (7.23), (7.24), (7.27), and (7.28) into Eq. (7.29), we obtain the alternative criteria of choice:
It can be seen in Eq. (7.30), as ![]() > 0, Eq. (7.1), that the Bayesian decision theory solution of the first bet points to option 1B as the predicted preferred choice.
> 0, Eq. (7.1), that the Bayesian decision theory solution of the first bet points to option 1B as the predicted preferred choice.
7.3.2 The Choosing of Option 2A
The outcome probability distributions of the options of the second bet are:
and

The corresponding utility probability distributions, for a monthly initial asset position of, say, ![]() for groceries and the like, are (Eq. 7.1):
for groceries and the like, are (Eq. 7.1):
and
The expected utilities of Eqs. (7.33) and (7.34) are, respectively (Eq. 7.5):
It can be seen in Eq. (7.35), as ![]() > 0, Eq. (7.1), that the expected utility solution of the second bet points to option 2B as the predicted preferred choice, which contradicts our basic intuition.
> 0, Eq. (7.1), that the expected utility solution of the second bet points to option 2B as the predicted preferred choice, which contradicts our basic intuition.
The standard deviation of Eqs. (7.33) and (7.34) are, respectively (Eq. 7.8):
It follows from Eqs. (7.35) and (7.36) that the ![]() sigma confidence intervals (Eqs. 7.7 and 7.11) of the utility probability distributions Eqs. (7.33) and (7.34) are, respectively:
sigma confidence intervals (Eqs. 7.7 and 7.11) of the utility probability distributions Eqs. (7.33) and (7.34) are, respectively:
and
The absolute minimal and maximal values (Eqs. 7.6 and 7.10) of the utility probability distributions Eqs. (7.33) and (7.34) are, respectively:
and
Comparing Eqs. (7.37)(7.38)(7.39), one sees that for the utility probability distribution Eq. (7.33) there is neither a lower bound undershoot nor an upper bound overshoot. It follows that for the first option of the second bet, the appropriate criterion of choice is the first row of Eq. (7.18):
Comparing Eqs. (7.38)(7.39)(7.40), one sees that for the utility probability distribution Eq. (7.34), an upper bound overshoot occurs. It follows that for the second option of the second bet, the appropriate criterion of choice is the third row of Eq. (7.18):
where ![]() . Substituting Eqs. (7.35), (7.36), (7.39), (7.40) into Eqs. (7.41) and (7.42), we obtain the alternative criteria of choice:
. Substituting Eqs. (7.35), (7.36), (7.39), (7.40) into Eqs. (7.41) and (7.42), we obtain the alternative criteria of choice:
It can be seen in Eq. (7.43), as ![]() > 0, Eq. (7.1), that the Bayesian decision theory solution of the second bet points to option 2A as the predicted preferred choice, which – unlike the expected utility solution Eq. (7.35) – corresponds to our basic intuition.
> 0, Eq. (7.1), that the Bayesian decision theory solution of the second bet points to option 2A as the predicted preferred choice, which – unlike the expected utility solution Eq. (7.35) – corresponds to our basic intuition.
7.3.3 How to Resolve an Allais Paradox
The Bayesian decision theory solution aligns itself with the basic intuition to “take the money and run,” i.e., the choosing of option 2A in the second bet, by taking into account the probabilistic worst- and best-case scenarios, as well as the most likely scenario. The probabilistic worst-case scenario (Eq. 7.9) under both options are (Eqs. 7.40):
The probabilistic most likely scenario (Eq. 7.5) under both options are (Eq. 7.35):
The probabilistic best-case scenario (Eq. 7.12) under both options are (Eqs. 7.40):
If we take the secure option 2A as our reference point, then this choice represents a probabilistic gain in the lower bound (Eq. 7.44):
a probabilistic loss in the expectation value (Eq. 7.45):
and a probabilistic loss in the upper bound (Eq. 7.46):
It follows that the secure option 2A represents a net probabilistic gain, as the gain in the lower bound compensates for the losses in both the expectation value and the upper bound (Eqs. 7.49):
for any ![]() > 0.
> 0.
According to Allais the fundamental psychological element of the theory of risk is the spread of the probabilities of the utility values around their mean [7]. The alternative criterion of choice takes this spread around the mean into account by way of the probabilistic worst- and best-case scenarios (Eqs. 7.44 and 7.46).
7.4 The Ellsberg Paradox
Ellsberg [8] presents two experiments, the first consisting of two urns with red and black balls, and the second a single urn with combinations of red, black, yellow balls. The first of these experiments is described here; the second experiment essentially shows the same results. Ellsberg's first urn experiment involves the two urns:
- Urn 1 – 100 balls, 50 red, 50 black;
- Urn 2 – 100 balls, red and black with proportions not specified,
with payoffs defined as:
- I. “Payoff on red1” – draw from urn 1, receive $1 if red, $0 if black;
- II. “Payoff on black1” – draw from urn 1, receive $0 if red, $1 if black;
- III. “Payoff on red2” – draw from urn 2, receive $1 if red, $0 if black;
- IV. “Payoff on black2” – draw from urn 2, receive $0 if red, $1 if black.
The gambles posed are:
- 1. Which do you prefer, “payoff on red1” or “payoff on black1”?
- 2. Which do you prefer, “payoff on red2” or “payoff on black2”?
- 3. Which do you prefer, “payoff on red1” or “payoff on red2”?
- 4. Which do you prefer, “payoff on black1” or “payoff on black2”?
Results according to Ellsberg, from introspection and non-experimental surveying of colleagues, are:
- a. Majority will be indifferent in gambles (1) and (2), which indicates that subjective probabilities of red versus black are 50/50 for both urn 1 and urn 2,
- b. Majority prefers red1 in (3) and black1 in (4) – in other words, most people prefer urn 1 (known 50/50) over urn 2 (unknown split between red and black).
The Ellsberg observations (a) and (b) become paradoxical only if one interprets the preference for urn 1 over urn 2 in the gambles (3) and (4) to mean that the probabilities for red1 and black1 are greater than the corresponding probabilities, red2 and black2. As such, an interpretation of observation (b) would be in contradiction with observation (a), which states that the probabilities of red1, red2, black1, and black2 are all 1/2. However, this paradox may be trivially resolved if one realizes that:
All things being equal probability wise, one is perfectly free to prefer one Ellsberg urn over the other without being inconsistent.
As one may witness a clear preference for the urn with known proportions over the urn with unknown proportions – i.e., observation (b) – we may conclude that people prefer gambles with crisp and clear probabilities to gambles with “fuzzy” probabilities, even if these probabilities are ultimately equivalent – i.e., observation (a). This preference is called “ambiguity aversion,” [8].
In closing, the Ellsberg observations (a) and (b) would only be paradoxical for, say, the alternative urns:
- Urn 1 – 100 balls, 25 red, 75 black;
- Urn 2 – 100 balls, red and black with proportions not specified,
as simple introspection suggests that for these alternative urns, one would prefer red2 over red1 and black1 over black2. This concludes our discussion of the Ellsberg paradox.
7.5 The Difference in Riskiness Between Type I and Type II Events
Due to many consistency problems with, on the one hand, predictive risk analysis and expected utility theory and, on the other hand, common-sense considerations of risk acceptability in some well-constructed counter-examples, it has been difficult to maintain the case for the feasibility of a predictive theory of choice – even to such an extent that one may read in a textbook like Reith [9] that the usefulness of the notion of “risk” lies not in its ability to correctly predict future outcomes, but rather in its ability to provide a basis for decision-making.
In van Erp et al. [3] it is postulated that the expectation value as an index of risk should be used with a critical mind, and that this value:
may lie at the heart of problems of expected utility theory to model choice preferences. For it is found that the alternative risk index (Eq. 7.18):
accommodates not only the Allais paradox, as previously discussed, but also the prospect theoretical counter-examples to expected utility theory; i.e., the reflection effect and the inverted S-shape in certainty bets (see van Erp et al. [3]). Moreover, this alternative risk index may also shed some light on common-sense observations such as the one made in Section 2.2 that most people judge a type II event as more undesirable than a type I event, even if the expected consequences of the two events are exactly the same.
In this section it will further be demonstrated that the alternative risk index (Eq. 7.52) will assign higher risks to type II events than to type I events, even if the expectation values of both events are so constructed that they are equal for both types of events.
7.5.1 Outcome Probability Distributions with Equal Expectation Values
Imagine that one has two dichotomous events, one of which is a type I event, ![]() , and the other a type II event,
, and the other a type II event, ![]() . If (i) the negative consequence of the type II event occurring is
. If (i) the negative consequence of the type II event occurring is ![]() times the negative consequence of the type I event occurring, (ii) the consequence of the non-occurrence of either event is zero, and (iii) the probability of the type II event is an
times the negative consequence of the type I event occurring, (ii) the consequence of the non-occurrence of either event is zero, and (iii) the probability of the type II event is an ![]() th fraction of the probability of the type I event, i.e.:
th fraction of the probability of the type I event, i.e.:
and
then both outcome probability distributions will admit the same expectation values, i.e.:
Note that in the outcome probability distributions (7.53) and (7.54) the negative consequences are represented by positive numbers, rather than negative numbers. As a consequence, the risk index Eq. (7.52) is to be minimized, rather than maximized.
7.5.2 The Risk of the Type I Event
Suppose that the type I event has a probability of occurring of:
Then the expectation value and standard deviation of the corresponding outcome probability distribution (7.55) are given as:
and
So the ![]() -sigma confidence bounds of Eq. (7.53) under Eq. (7.56) are given as Eqs. (7.57) and (7.58):
-sigma confidence bounds of Eq. (7.53) under Eq. (7.56) are given as Eqs. (7.57) and (7.58):
and
If one corrects for lower bound undershoot and upper bound overshoot, then the corrected confidence bounds are (Eqs. 7.53 and 7.59):
Substituting Eqs. (7.57), (7.61), and (7.62) into the left-hand side of Eq. (7.52) one obtains a computed risk for the type I event of:
for any sigma level k. So, for the particular case of Eqs. (7.53) and (7.56), the alternative criterion of choice (Eq. 7.52) collapses to the traditional expectation value (Eq. 7.57) as the criterion of choice.
7.5.3 The Risk of the Type II Event
Assume that the type II event has an ![]() times smaller probability of occurring than the type I event, and the consequence of the type II event is
times smaller probability of occurring than the type I event, and the consequence of the type II event is ![]() times larger than the consequence of the type I event (Eqs. 7.53 and 7.54). The expectation value and standard deviation of the type II outcome probability distribution is given as (Eq. 7.55):
times larger than the consequence of the type I event (Eqs. 7.53 and 7.54). The expectation value and standard deviation of the type II outcome probability distribution is given as (Eq. 7.55):
and
So the ![]() -sigma confidence bounds of Eq. 7.54 under Eq. (7.56) are given as (Eqs. 7.64 and 7.65):
-sigma confidence bounds of Eq. 7.54 under Eq. (7.56) are given as (Eqs. 7.64 and 7.65):
and
If one corrects for lower bound undershoot and upper bound overshoot, then the corrected confidence bounds are (Eqs. 7.54 and 7.66):
Substituting Eqs. (7.64), (7.68), and (7.69) into the left-hand side of Eq. 7.52, one may obtain for the high–impact, low-probability (HILP) event the following risk index as a function of the chosen ![]() -sigma level:
-sigma level:
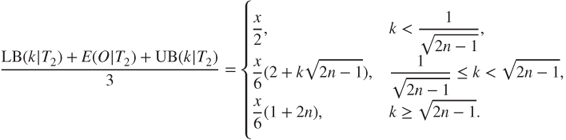
For both large ![]() , i.e., pronounced type II events, and
, i.e., pronounced type II events, and ![]() -sigma levels in the reasonable range of, say, 1–6, or, equivalently,
-sigma levels in the reasonable range of, say, 1–6, or, equivalently, ![]() , the risk (Eq. 7.52), of the type II event translates to:
, the risk (Eq. 7.52), of the type II event translates to:
So, for the particular case of Eqs. (7.54) and 7.56, and a variable ![]() much greater than 1, i.e., n ≫ 1, the alternative criterion of choice (Eq. 7.52), goes to a value differing markedly from the traditional expectation value (Eq. 7.57).
much greater than 1, i.e., n ≫ 1, the alternative criterion of choice (Eq. 7.52), goes to a value differing markedly from the traditional expectation value (Eq. 7.57).
7.5.4 Comparing the Risks of the Type I and Type II Events
The type I event, ![]() , is operationalized in this section as an event having a probability of
, is operationalized in this section as an event having a probability of ![]() and a loss of
and a loss of ![]() (Eqs. 7.53 and 7.56). The type II event,
(Eqs. 7.53 and 7.56). The type II event, ![]() , is operationalized relative to the type I event as the event that has a probability
, is operationalized relative to the type I event as the event that has a probability ![]() times smaller and a loss
times smaller and a loss ![]() times
times ![]() greater (Eqs. 7.54 and 7.56), i.e., the more severe the type II event, the less likely its occurrence.
greater (Eqs. 7.54 and 7.56), i.e., the more severe the type II event, the less likely its occurrence.
The expectation values of the type I and type II events are equal (Eq. 7.55). Nonetheless, for a given “severity” variable ![]() > 1, the alternative risk index (Eq. 7.52) will assign a higher risk to the type II event than to the type I event by a factor of (Eqs. 7.63 and 7.71):
> 1, the alternative risk index (Eq. 7.52) will assign a higher risk to the type II event than to the type I event by a factor of (Eqs. 7.63 and 7.71):
If for ![]() sigma levels the risk ratio Eq. 7.72 is plotted as a function of the severity variable
sigma levels the risk ratio Eq. 7.72 is plotted as a function of the severity variable ![]() , Figure 7.1 is obtained.
, Figure 7.1 is obtained.

Figure 7.1 Risk ratios as a function of the severity variable  .
.
In Figure 7.1 it can be seen that for a severity variable ![]() , or, equivalently, a probability of
, or, equivalently, a probability of ![]() for the type II event and losses that are an order of magnitude of
for the type II event and losses that are an order of magnitude of ![]() more severe than those under a type I event having a probability of
more severe than those under a type I event having a probability of ![]() , and sigma levels of
, and sigma levels of ![]() , one observes risk ratios of about 333, 667, 1000, and 2000, respectively, as may be seen from Eq. 7.72:
, one observes risk ratios of about 333, 667, 1000, and 2000, respectively, as may be seen from Eq. 7.72:

So, the adjusted criterion of choice (Eq. 7.52) – which is the location measure taking into account the probabilistic worst-case scenario, expected scenario, and best-case scenario (Eq. 7.18) – corroborates and quantifies the common-sense observation that most people judge a type II event as more undesirable than a type I event, even if the expected consequences of the two events are exactly the same.
7.6 Discussion
Although it seems barely conceivable today, the historical record shows clearly and repeatedly that the notion of “expectation of profit” to the first researchers in probability theory was perhaps even more intuitive than the notion of probability itself [5]. Moreover, it was so obvious to many that a person acting in pure self-interest should always behave in such a way as to maximize the expected profit that the prosperous merchants in seventeenth-century Amsterdam bought and sold mathematical expectations as if they were tangible goods.
A new insight into risk science came in 1738 with the St. Petersburg paper [1]. This paper is truly important on the subject of risk as well as on human behavior, as it introduced the pivotal idea that the true value to a person of receiving a certain amount of money is not measured simply by the amount received; it also depends upon how much the person already possesses: “Utility resulting from any small increase in wealth will be inversely proportionate to the quantity of goods previously possessed.” This idea is as simple as it is intuitive. For it stands to reason that a beggar will assign a much higher utility to the gain of a thousand euros than will a billionaire, and a modern economist is expressing the same idea when he speaks of the “diminishing marginal utility of wealth.” So, where decision theory, by way of the maximization of the expectation of profit, hitherto had only taken profits and the probabilities of these profits materializing into account, Daniel Bernoulli identified the initial wealth of the decision-maker as a third decision theoretical factor of consequence.
Bernoulli's expected utility theory laid the intellectual groundwork for many aspects of microeconomic theory and decision theory. Furthermore, by way of its utility function – which measures that which cannot be counted – it also managed to elevate psychology in 1860 from a mere metaphysical pastime to an exact science [2], as it was found by Fechner that Bernoulli's utility function could model our perception of sensory stimuli for a given background stimulus intensity [10]. The decibel scale, for example, is an instance where Bernoulli's utility function converts objective loudness stimuli to a corresponding subjective scale. Moreover, with the introduction of operational risk management in the mid-twentieth century, in the aftermath of the Second World War and at the beginning of the atomic era, Bernoulli's expected utility theory has remained as relevant as ever. Many improvements by many authors have been proposed to Bernoulli's initial 1738 proposal, the most notable of these being game theory and its offshoots [4, 11] and prospect theory [12].
von Neumann and Morgenstern [4] formulated a lofty predictive mathematical theory on their axiomatic scaffolding and proclaimed that their theory had superseded Bernoulli's expected utility theory as a more general theory. But Tversky and Kahneman were then quick to point out that both von Neumann and Morgenstern's game theory and Bernoulli's expected utility theory could be demonstrated to violate common-sense rationality in certain instances and, as a reaction, counter-postulated that human rationality can never be captured by simple mathematical maximization principles [13]. Tversky and Kahneman then proceeded to propose a mathematical descriptive decision theory that was rooted in empirical observation of psychological betting experiments, rather than abstract mathematical first principles [12].
So persuasive was the case made by Tversky and Kahneman that the descriptive paradigm of behavioral economics came to dominate the decision theoretical field. But just as prospect theory, in its initial inception, was mainly a reaction to von Morgenstern and Neumann's game theory, which put too high a premium on mathematics, while failing to appeal to our common sense, so the Bayesian decision theory [3] is a reaction to Tversky's and Kahneman prospect theory, which puts too high a premium on bare bones empiricism of hypothetical betting experiments, while failing to appeal to our mathematical need for compelling first principles.
A Bayesian decision theoretical research program for the future is one where all the reported inconsistencies of expected utility theory are reassessed and where it is studied if these inconsistencies – if legitimate inconsistencies – may resolve themselves by applying this neo-Bernoullian utility theory. Moreover, it should be gauged how much of prospect theory, which, like the Bayesian decision theory, purports to resolve the inconsistencies that have plagued expected utility theory, remains relevant after: (i) the utility function of the utility theory is set to Bernoulli's original 1738 proposal (see Section 7.1); and (ii) the expectation value is replaced by the alternative position measure, which not only takes into account the most likely scenario – in the probabilistic sense – but also the worst- and best-case scenarios (see Section 7.2.2). The potential benefit of such a research program would be that it might establish the Bayesian decision theory as the normative theory of risk which accurately predicts the way people choose when faced with uncertain outcomes. Such a normative theory of risk could be a boon for operational risk management, as it would put at their disposal a simple but effective mathematical tool to guide them in their decision-making.
7.7 Conclusions
We have introduced in this chapter the Bayesian decision theory as an improvement on Bernoulli's utility theory and as an alternative to prospect theory. It has been demonstrated that this neo-Bernoullian utility theory accommodates, non-trivially, the Allais paradox and the common-sense observation that type II events are more risky than type I events, as well as – very trivially, as the Ellsberg paradox is arguably not that paradoxical – the Ellsberg paradox. In Section 8.12 the Bayesian decision theory will be applied to a simple non-trivial decision problem. It will be demonstrated in this decision theoretical toy problem that the alternative criterion of choice (Eq. 7.18), relative to the traditional criterion of choice (Eq. 7.5), leads to a more realistic estimation of hypothetical benefits of type II risk barriers.
References
- [1] Bernoulli, D. (1738). Exposition of a New Theory on the Measurement of Risk. Translated from Latin into English by Dr Louise Sommer from ‘Specimen Theoriae Novae de Mensura Sortis’, Commentarii Academiae Scientiarum Imperialis Petropolitanas, Tomus V, pp. 175–192.
- [2] Fancher, R.E. (1990). Pioneers of Psychology. W.W. Norton and Company, London.
- [3] van Erp, H.R.N., Linger, R.O., Van Gelder, P.H.A.J.M. (2015). Fact Sheet Research on Bayesian Decision Theory. 1409.8269v4 arXiv. Online: http://arxiv.org/abs/1409.8269 (accessed March 2016).
- [4] von Neumann, J., Morgenstern, O. (1944). Theory of Games and Economic Behavior, Princeton, NJ, Princeton University Press.
- [5] Jaynes, E.T. (2003). Probability Theory; the Logic of Science. Cambridge University Press, Cambridge.
- [6] Lindgren, B.W. (1993). Statistical Theory. Chapman & Hall, Inc., New York.
- [7] Allais, M. (1988). An Outline of My Main Contributions to Economic Science. Nobel Lecture, December 9.
- [8] Ellsberg D. (1961). Risk, ambiguity, and the savage axioms. Quarterly Journal of Economics, 75, 643–699.
- [9] Reith, G. (2009). Uncertain times: the notion of ‘risk’ and the development of modernity, In: The Earthscan Reader on Risk (eds Lofstedt, R. & Boholm, A.). Earthscan, London.
- [10] Masin S.C., Zudini V., Antonelli M. (2009). Early alternative derivations of Fechner's law. Journal of Behavioural Sciences, 45, 56–65.
- [11] Savage, L.J. (1954). The Foundations of Statistics. John Wiley & Sons, Inc., New York.
- [12] Tversky A., Kahneman D. (1992). Advances in prospect theory: cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5, 297–323.
- [13] Bernstein, P.L. (1998). Against the Gods. The Remarkable Story of Risk. John Wiley & Sons, Inc., New York.


















