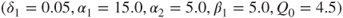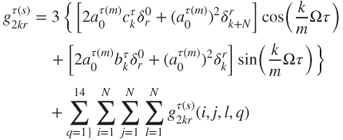
with
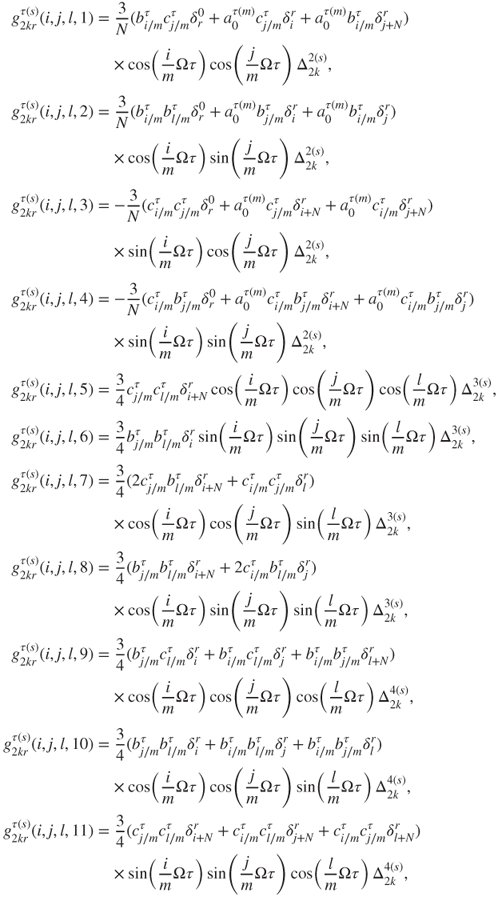
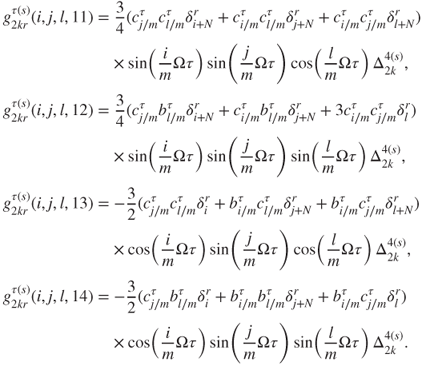
The matrices relative to the velocity are
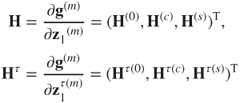
where
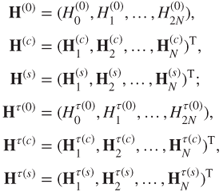
for ![]() with
with
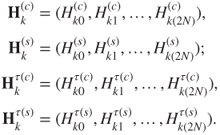
for ![]() The corresponding components are
The corresponding components are
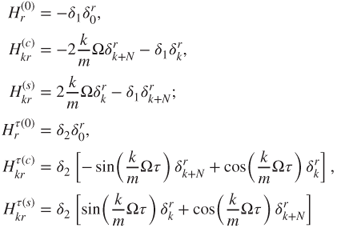
for ![]() .
.
The corresponding eigenvalues of equilibrium are determined by
From Luo (2012a), the eigenvalues of ![]() are classified as
are classified as
If ![]()
![]() , the approximate solution of periodic motion relative to
, the approximate solution of periodic motion relative to ![]() with truncation of
with truncation of ![]() and
and ![]() is stable. If
is stable. If ![]()
![]() , the truncated approximate solution relative to
, the truncated approximate solution relative to ![]() is unstable. The corresponding boundary between the stable and unstable solutions is given by the saddle-node bifurcation and Hopf bifurcation.
is unstable. The corresponding boundary between the stable and unstable solutions is given by the saddle-node bifurcation and Hopf bifurcation.
6.2 Analytical Bifurcation Trees
The harmonic amplitude varying with excitation frequency ![]() is presented to illustrate the bifurcation tree of period-1 motion to chaos. The harmonic amplitude and phase are defined by
is presented to illustrate the bifurcation tree of period-1 motion to chaos. The harmonic amplitude and phase are defined by
The corresponding solution in Equation (6.2) becomes
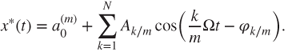
As in Luo and Jin (2014), consider a time-delayed, quadratic nonlinear oscillator under a periodic excitation with system parameters as
From the prescribed system parameters, an overview of the bifurcation tree of period-1 motion to chaos for the time-delayed, quadratic nonlinear oscillator will be presented in Figure 6.1 through the 160 harmonic terms (HB160). In Figure 6.1(i), the constant varying with excitation frequency is presented. For ![]() , the period-1 motion exists. In Figure 6.1(ii), the harmonic amplitude
, the period-1 motion exists. In Figure 6.1(ii), the harmonic amplitude ![]() versus excitation frequency is presented for period-8 motion only. Such amplitudes for period-1, period-2, and period-4 motions are zero. The saddle-node and Hopf bifurcations occur at
versus excitation frequency is presented for period-8 motion only. Such amplitudes for period-1, period-2, and period-4 motions are zero. The saddle-node and Hopf bifurcations occur at ![]() and
and ![]() , respectively. Once the Hopf bifurcation occurs, the period-16 motions can be similarly determined by the 320 harmonic terms. Many coexisting unstable period-8 motions are observed. In Figure 6.1(iii), harmonic amplitude
, respectively. Once the Hopf bifurcation occurs, the period-16 motions can be similarly determined by the 320 harmonic terms. Many coexisting unstable period-8 motions are observed. In Figure 6.1(iii), harmonic amplitude ![]() varying with excitation frequency is presented for period-4 and period-8 motions. The saddle-node and Hopf bifurcations of period-4 motion occur at
varying with excitation frequency is presented for period-4 and period-8 motions. The saddle-node and Hopf bifurcations of period-4 motion occur at ![]() and
and ![]() . Such harmonic amplitudes for period-1 and period-2 motions are zero. In Figure 6.1(iv), the harmonic amplitude
. Such harmonic amplitudes for period-1 and period-2 motions are zero. In Figure 6.1(iv), the harmonic amplitude ![]() versus excitation frequency is presented that is similar to the harmonic amplitude
versus excitation frequency is presented that is similar to the harmonic amplitude ![]() for period-8 motion only herein. In Figure 6.1(v), the harmonic amplitude
for period-8 motion only herein. In Figure 6.1(v), the harmonic amplitude ![]() varying with excitation frequency is presented for period-2, period-4, and period-8 motions. The saddle-node and Hopf bifurcations of period-2 motion occur at
varying with excitation frequency is presented for period-2, period-4, and period-8 motions. The saddle-node and Hopf bifurcations of period-2 motion occur at ![]() and
and ![]() . Such harmonic amplitude for period-1 motion is zero. The harmonic amplitudes
. Such harmonic amplitude for period-1 motion is zero. The harmonic amplitudes ![]()
![]() will not be presented to reduce illustrations. In Figure 6.1(vi), the primary harmonic amplitude
will not be presented to reduce illustrations. In Figure 6.1(vi), the primary harmonic amplitude ![]() versus excitation frequency is presented, and the Hopf bifurcation of period-1 motion occurs at
versus excitation frequency is presented, and the Hopf bifurcation of period-1 motion occurs at ![]() . The amplitude peak is around
. The amplitude peak is around ![]() . To check the amplitude decrease, the harmonic amplitudes
. To check the amplitude decrease, the harmonic amplitudes ![]() and
and ![]() versus excitation frequency are presented with common logarithm scale in Figure 6.1(vii),(viii), respectively. The harmonic amplitudes drop dramatically with increasing excitation frequency. However, for small excitation frequency, the harmonic amplitudes do not change too much. Thus, the variation of harmonic amplitude
versus excitation frequency are presented with common logarithm scale in Figure 6.1(vii),(viii), respectively. The harmonic amplitudes drop dramatically with increasing excitation frequency. However, for small excitation frequency, the harmonic amplitudes do not change too much. Thus, the variation of harmonic amplitude ![]() with excitation frequency is presented in Figure 6.1(ix). Two Hopf bifurcations of period-1 motions are at
with excitation frequency is presented in Figure 6.1(ix). Two Hopf bifurcations of period-1 motions are at ![]() . The stable period-1 motion also exists
. The stable period-1 motion also exists ![]() .
.
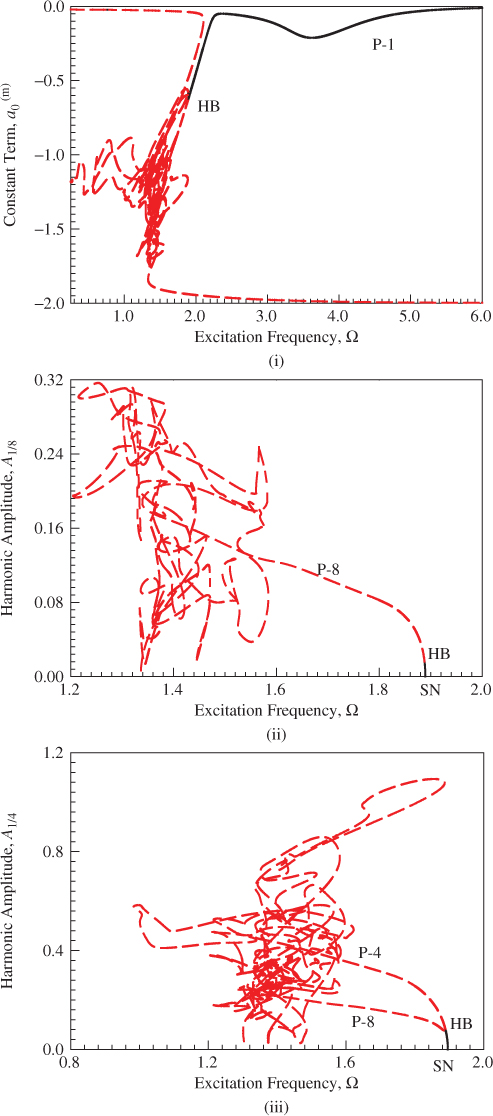
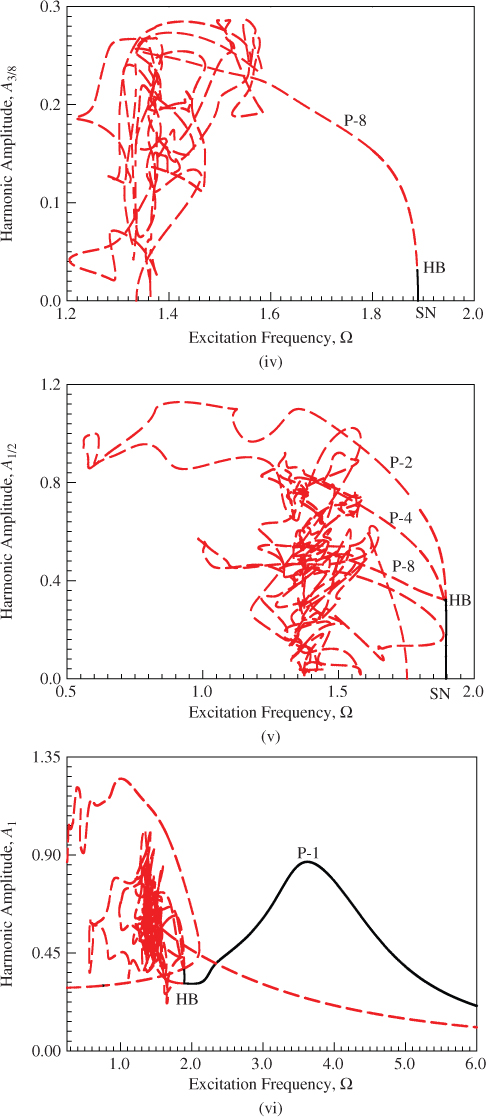
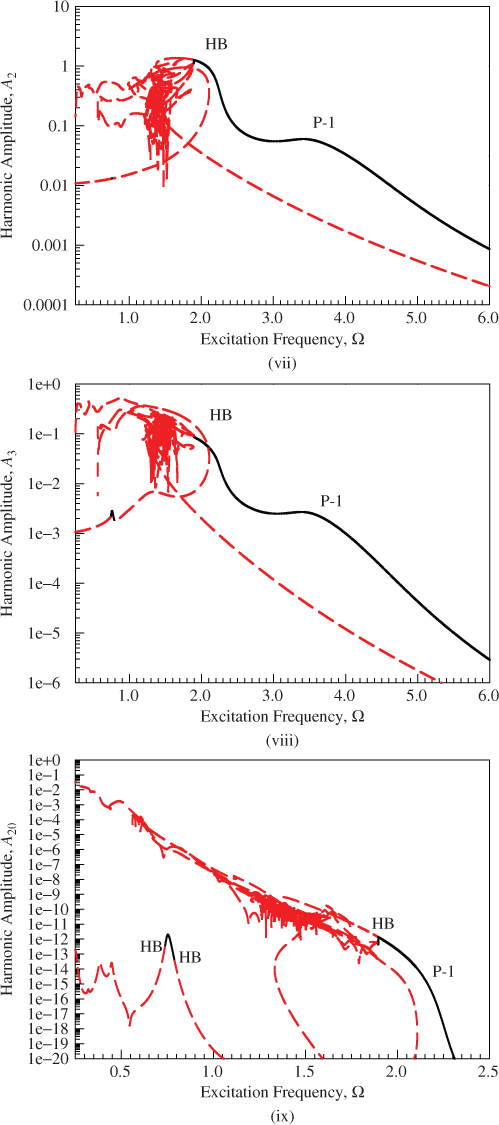
Figure 6.1 An overview for the analytical prediction of period-1 to period-8 motions of the time-delayed, quadratic nonlinear oscillator based on the 160 harmonic terms (HB160): (i)  and (ii)–(ix)
and (ii)–(ix) 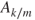
 . Parameters:
. Parameters: 
The local view of the bifurcation tree of period-1 to period-8 motion is presented in Figure 6.2 in the range of ![]() . In Figure 6.2(i), the constant term
. In Figure 6.2(i), the constant term ![]() versus excitation frequency is presented. The bifurcation tree of period-1 to period-8 motion is clearly observed. The Hopf bifurcation of period-1 motion gives the birth of the period-2 motion. The Hopf bifurcation of period-2 motion gives the birth of the period-4 motion, and the Hopf bifurcation of period-4 motion is the onset of period-8 motion. The Hopf bifurcation of period-8 motion can generate period-16 motion. In addition, the unstable period-1 to period-8 motions are presented. For this local view, the constant term is located in the range of
versus excitation frequency is presented. The bifurcation tree of period-1 to period-8 motion is clearly observed. The Hopf bifurcation of period-1 motion gives the birth of the period-2 motion. The Hopf bifurcation of period-2 motion gives the birth of the period-4 motion, and the Hopf bifurcation of period-4 motion is the onset of period-8 motion. The Hopf bifurcation of period-8 motion can generate period-16 motion. In addition, the unstable period-1 to period-8 motions are presented. For this local view, the constant term is located in the range of ![]() . In Figure 6.2(ii), the harmonic amplitude
. In Figure 6.2(ii), the harmonic amplitude ![]() varying with excitation frequency is presented for period-8 motion only. In the specific excitation range, the harmonic amplitude
varying with excitation frequency is presented for period-8 motion only. In the specific excitation range, the harmonic amplitude ![]() In Figure 6.2(iii), the local view of the bifurcation tree of period-4 to period-8 motion is presented through the harmonic amplitude
In Figure 6.2(iii), the local view of the bifurcation tree of period-4 to period-8 motion is presented through the harmonic amplitude ![]() . Such harmonic amplitude
. Such harmonic amplitude ![]() lies in the range of
lies in the range of ![]() In Figure 6.2(iv), the harmonic amplitude
In Figure 6.2(iv), the harmonic amplitude ![]() is presented that is similar to the harmonic amplitude
is presented that is similar to the harmonic amplitude ![]() for period-8 motion only. In Figure 6.2(v), the harmonic amplitude
for period-8 motion only. In Figure 6.2(v), the harmonic amplitude ![]() is presented for the bifurcation tree of period-2 to period-8 motion. The bifurcation structure from period-2 to period-8 motion is very clearly shown. The harmonic amplitude
is presented for the bifurcation tree of period-2 to period-8 motion. The bifurcation structure from period-2 to period-8 motion is very clearly shown. The harmonic amplitude ![]() is observed for period-2, period-4, and period-8 motions. To avoid abundant illustrations, the primary harmonic amplitude
is observed for period-2, period-4, and period-8 motions. To avoid abundant illustrations, the primary harmonic amplitude ![]() in the local view of bifurcation tree is presented in Figure 6.2(vi). The harmonic amplitude
in the local view of bifurcation tree is presented in Figure 6.2(vi). The harmonic amplitude ![]() for the bifurcation tree of period-1 to period-8 motion lies in the range of
for the bifurcation tree of period-1 to period-8 motion lies in the range of ![]() in the prescribed excitation frequency range, as shown in Figure 6.2(vii). The harmonic amplitude
in the prescribed excitation frequency range, as shown in Figure 6.2(vii). The harmonic amplitude ![]() is presented in Figure 6.2(viii), and the bifurcation tree for period-1 to period-8 motion is clearly illustrated. Finally, the harmonic amplitude
is presented in Figure 6.2(viii), and the bifurcation tree for period-1 to period-8 motion is clearly illustrated. Finally, the harmonic amplitude ![]() for the bifurcation tree of period-1 motion to period-8 motion is presented in Figure 6.2(ix). The range of the amplitude
for the bifurcation tree of period-1 motion to period-8 motion is presented in Figure 6.2(ix). The range of the amplitude ![]() lies in the range of
lies in the range of ![]() .
.
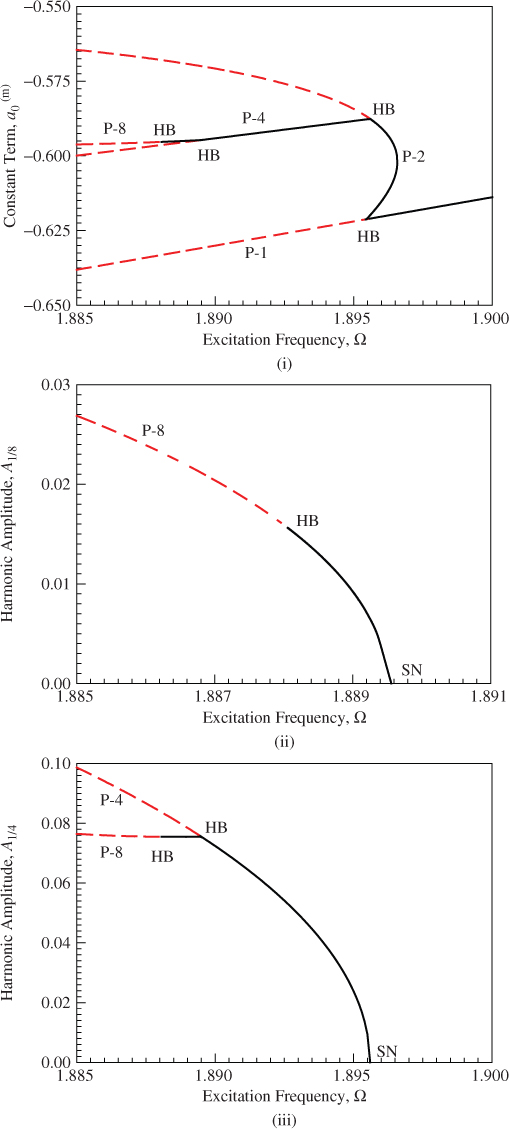
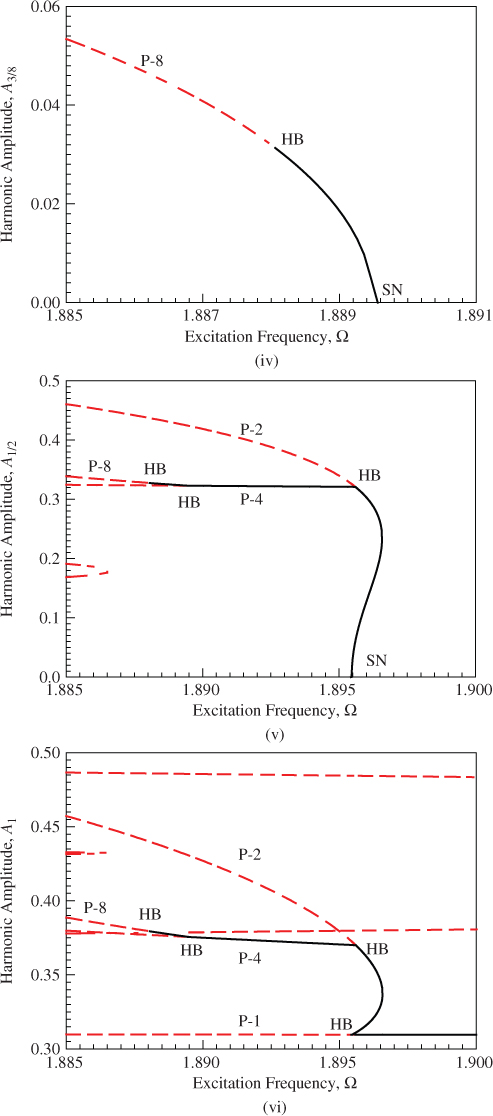
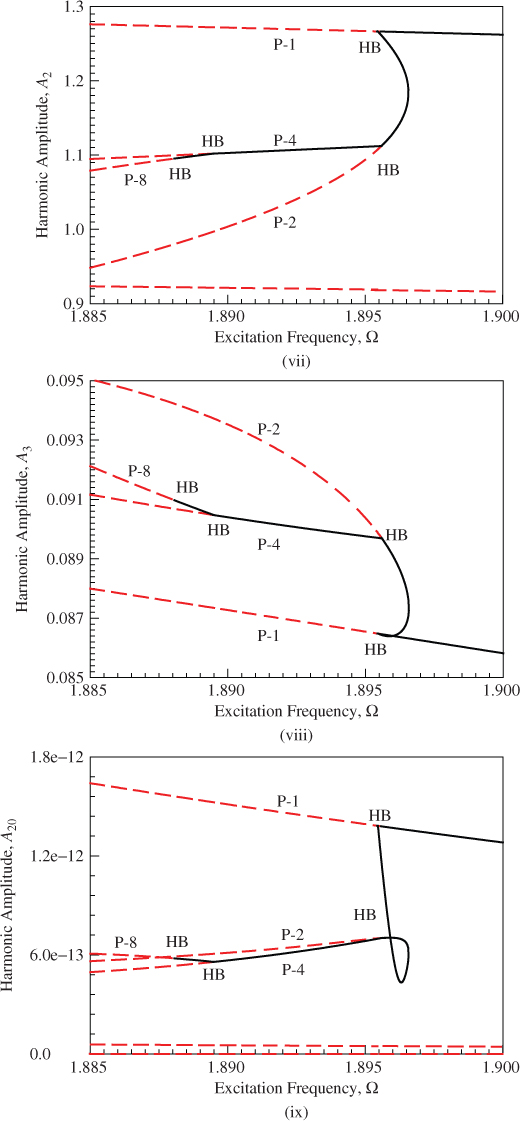
Figure 6.2 The zoomed view for the analytical prediction of period-1 to period-8 motions based on the 160 harmonic terms (HB160): (i)  and (ii)–(ix)
and (ii)–(ix) 
 . Parameters:
. Parameters: 
6.3 Illustrations of Periodic Motions
The initial conditions and the initial time-delay values for ![]() for numerical simulation are computed from the analytical solution. The numerical and analytical results are depicted by solid curves and red circular symbols, respectively. The big filled circular symbols are initial conditions and initial time-delay response values. The delay initial starting and delay initial final points are represented by acronyms D.I.S. and D.I.F., respectively.
for numerical simulation are computed from the analytical solution. The numerical and analytical results are depicted by solid curves and red circular symbols, respectively. The big filled circular symbols are initial conditions and initial time-delay response values. The delay initial starting and delay initial final points are represented by acronyms D.I.S. and D.I.F., respectively.
As in Luo and Jin (2014), the displacement, velocity, trajectory and amplitude spectrum of stable period-1 motion for the time-delayed, quadratic nonlinear oscillator are presented in Figure 6.3 for ![]() with initial condition
with initial condition ![]() with initial time-delayed responses. This analytical solution is based on 20 harmonic terms (HB20) in the Fourier series solution of period-1 motion. In Figure 6.3(a),(b), for over 100 periods, the analytical and numerical solutions of the period-1 motion in the time-delayed, quadratic nonlinear oscillator match very well. The initial time-delayed displacement and velocity are presented by the large circular symbols for the initial delay period of
with initial time-delayed responses. This analytical solution is based on 20 harmonic terms (HB20) in the Fourier series solution of period-1 motion. In Figure 6.3(a),(b), for over 100 periods, the analytical and numerical solutions of the period-1 motion in the time-delayed, quadratic nonlinear oscillator match very well. The initial time-delayed displacement and velocity are presented by the large circular symbols for the initial delay period of ![]() In Figure 6.3(c), analytical and numerical trajectories match very well, and the initial time-delay responses in phase plane is clearly depicted. In Figure 6.3(d), the amplitude spectrum is presented. The quantity levels of the harmonic amplitudes are
In Figure 6.3(c), analytical and numerical trajectories match very well, and the initial time-delay responses in phase plane is clearly depicted. In Figure 6.3(d), the amplitude spectrum is presented. The quantity levels of the harmonic amplitudes are ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() The harmonic amplitudes decrease with harmonic order non-uniformly. The main contributions for this periodic motion are from the primary and second harmonics. The truncated harmonic amplitude is
The harmonic amplitudes decrease with harmonic order non-uniformly. The main contributions for this periodic motion are from the primary and second harmonics. The truncated harmonic amplitude is ![]() .
.

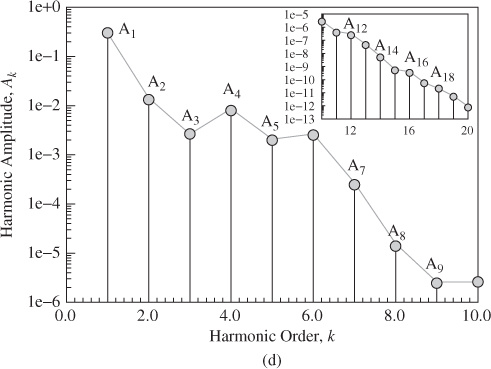
Figure 6.3 Analytical and numerical solutions of stable period-1 motion based on 48 harmonic terms (HB48): (a) displacement, (b) velocity, (c) phase plane, and (d) amplitude spectrum. Initial condition 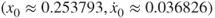 . Parameters:
. Parameters: 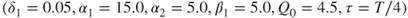
The trajectory and amplitude spectrum of stable period-1 motion for the time-delayed, quadratic nonlinear oscillator are presented in Figure 6.4 for ![]() and
and ![]() . The initial conditions are listed in Table 6.1 and initial time-delayed values are also computed from the analytical conditions. This analytical solution is based on 20 harmonic terms (HB20) in the Fourier series solution of period-1 motion. In Figure 6.4(a), analytical and numerical trajectories is presented for
. The initial conditions are listed in Table 6.1 and initial time-delayed values are also computed from the analytical conditions. This analytical solution is based on 20 harmonic terms (HB20) in the Fourier series solution of period-1 motion. In Figure 6.4(a), analytical and numerical trajectories is presented for ![]() , and the initial time-delay responses in the phase plane is illustrated, and this period-1 motion possesses two cycles. In Figure 6.4(b), the amplitude spectrum is presented. The main harmonic amplitudes are
, and the initial time-delay responses in the phase plane is illustrated, and this period-1 motion possesses two cycles. In Figure 6.4(b), the amplitude spectrum is presented. The main harmonic amplitudes are ![]()
![]()
![]()
![]() and
and ![]()
![]() The other harmonic amplitudes are
The other harmonic amplitudes are ![]() for
for ![]()
![]() In Figure 6.4(c), analytical and numerical trajectories with the initial time-delay values are presented for
In Figure 6.4(c), analytical and numerical trajectories with the initial time-delay values are presented for ![]() In Figure 6.4(d), the amplitude spectrum distribution is presented. The main harmonic amplitudes are
In Figure 6.4(d), the amplitude spectrum distribution is presented. The main harmonic amplitudes are ![]() and
and ![]() The other harmonic amplitudes are
The other harmonic amplitudes are ![]() for
for ![]()

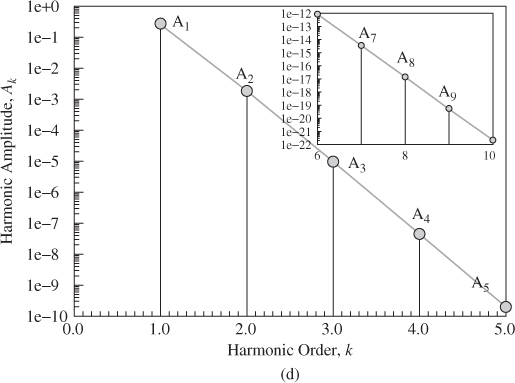
Figure 6.4 Phase plane and amplitude spectrums of period-1 motions: (a,b) 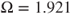 with
with 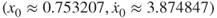 . (c,d)
. (c,d) 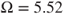 with
with 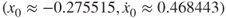 . Parameters:
. Parameters: 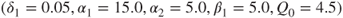
Table 6.1 Input data for numerical illustrations ![]()
| Figure no. | Initial condition |
Types | Harmonics terms | |
| Figure 6.4(a),(b) | 1.921 | (−0.753207, 3.874847) | P-1 | HB20 (stable) |
| Figure 6.4(c),(d) | 5.52 | (−0.275515, 0.468443) | P-1 | HB20 (stable) |
| Figure 6.11(i),(ii) | 1.8965 | (0.258268, 4.712170) | P-2 | HB40 (stable) |
| Figure 6.11(iii),(iv) | 1.8920 | (−0.788258, 0.116180) | P-4 | HB80 (stable) |
| Figure 6.11(v),(vi) | 1.88876 | (−0.319273, 4.696123) | P-8 | HB160 (stable) |
The stable period-2, period-4, and period-8 motions are presented in Figure 6.5 at ![]() for illustrations of complexity of periodic motions. The initial conditions for such stable periodic motions are listed in Table 6.1. In Figure 6.5(i), the analytical and numerical trajectories of a period-2 motion are presented. Such a period-2 motion possesses four cycles and the initial time-delay conditions are presented. The harmonic amplitude distribution is presented in Figure 6.5(ii). The main amplitudes of the period-2 motion in such time-delayed, nonlinear system are
for illustrations of complexity of periodic motions. The initial conditions for such stable periodic motions are listed in Table 6.1. In Figure 6.5(i), the analytical and numerical trajectories of a period-2 motion are presented. Such a period-2 motion possesses four cycles and the initial time-delay conditions are presented. The harmonic amplitude distribution is presented in Figure 6.5(ii). The main amplitudes of the period-2 motion in such time-delayed, nonlinear system are ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() and
and ![]() The other harmonic amplitudes are
The other harmonic amplitudes are ![]() for
for ![]() . The biggest contribution is from the harmonic term of
. The biggest contribution is from the harmonic term of ![]() In Figure 6.5(iii), the analytical and numerical trajectories of period-4 motion are presented. Such a period-4 motion possesses eight cycles and the initial time-delay conditions are presented. The harmonic amplitude distribution is presented in Figure 6.5(iv). The main amplitudes of the period-4 motion are
In Figure 6.5(iii), the analytical and numerical trajectories of period-4 motion are presented. Such a period-4 motion possesses eight cycles and the initial time-delay conditions are presented. The harmonic amplitude distribution is presented in Figure 6.5(iv). The main amplitudes of the period-4 motion are ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() and
and ![]()
![]() The other harmonic amplitudes are
The other harmonic amplitudes are ![]() for
for ![]() . The biggest contribution of the period-4 motion is from the harmonic amplitude of
. The biggest contribution of the period-4 motion is from the harmonic amplitude of ![]() In Figure 6.5(v), the analytical and numerical trajectories of a period-8 motion are presented. Such a period-8 motion possesses 16 cycles and the initial time-delay conditions are presented. The harmonic amplitude spectrum is presented in Figure 6.5(vi). The main harmonic amplitudes of a period-8 motion are
In Figure 6.5(v), the analytical and numerical trajectories of a period-8 motion are presented. Such a period-8 motion possesses 16 cycles and the initial time-delay conditions are presented. The harmonic amplitude spectrum is presented in Figure 6.5(vi). The main harmonic amplitudes of a period-8 motion are ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() and
and ![]() The other harmonic amplitudes are
The other harmonic amplitudes are ![]() for
for ![]() . The biggest contribution is still from the harmonic amplitude of
. The biggest contribution is still from the harmonic amplitude of ![]()
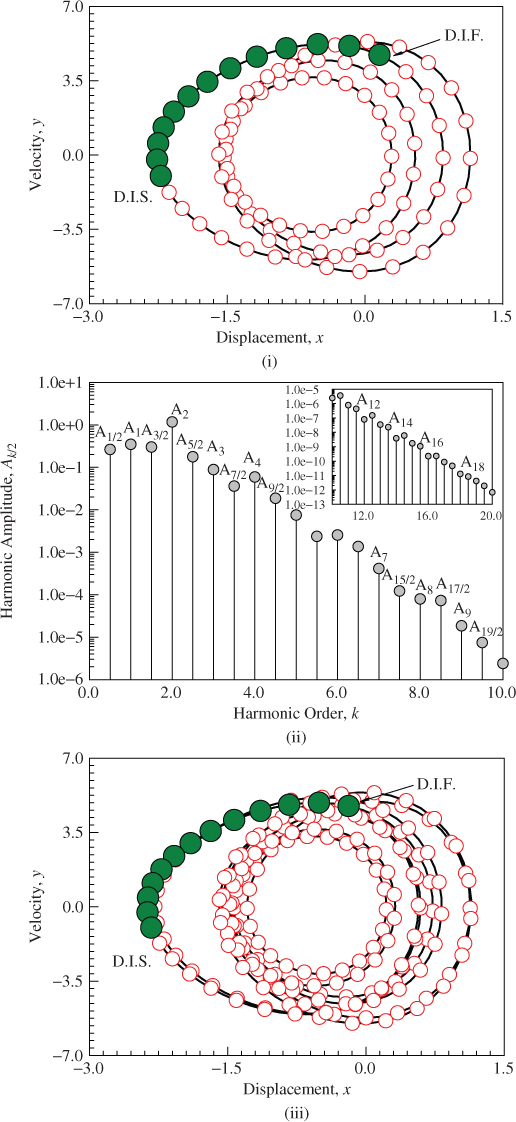
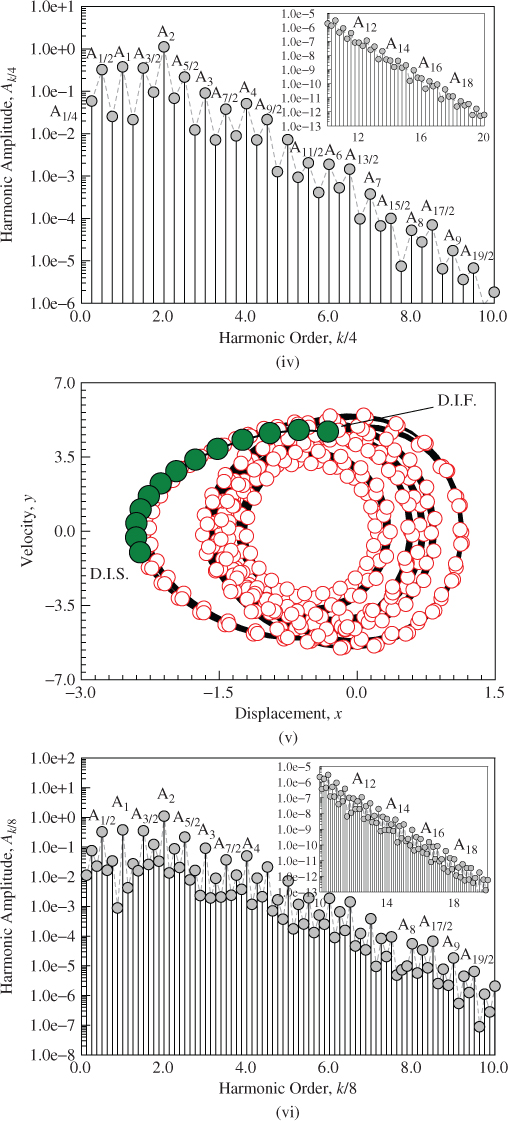
Figure 6.5 Phase plane and amplitude spectrums: (i,ii) period-2 motion (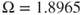 ,
, 
 HB40), (iii,iv) period-4 motion (
HB40), (iii,iv) period-4 motion (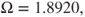
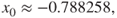
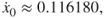 HB80), and (v,vi) period-8 motions (
HB80), and (v,vi) period-8 motions (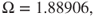
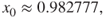
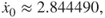 HB160).
HB160).