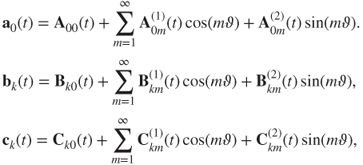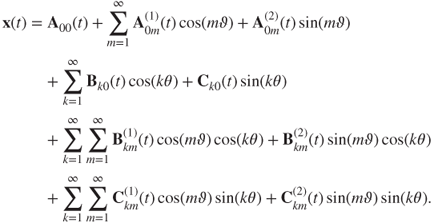Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Chapter 3
An Analytical Method for Periodic Flows

In this chapter, from Luo (2012a), the analytical dynamics of periodic flows and chaos in nonlinear dynamical systems will be presented. The analytical solutions of periodic flows and chaos in autonomous systems will be discussed first, and the analytical dynamics of non-autonomous nonlinear dynamical systems will be presented. The analytical solutions of periodic motions in free and periodically excited vibration systems will be presented. In a similar fashion, the analytical solutions of periodic flows for time-delayed nonlinear systems will be presented with/without periodic excitations, and time-delayed nonlinear vibration systems will also be discussed for engineering applications. The analytical solutions of periodic flows and chaos are independent of the small parameters, which are different from the traditional perturbation methods. The methodology presented herein will end the history of chaos being numerically simulated only.

3.1 Nonlinear Dynamical Systems

In this section, analytical periodic flows in autonomous and periodically forced, nonlinear dynamical systems will be discussed. A generalized harmonic balance method with the Fourier series expressions will be presented for such analytical, periodic flows, and chaos in nonlinear dynamical systems. The local stability and bifurcation theory of equilibriums in nonlinear autonomous systems of coefficients in the Fourier series solutions will be employed to classify analytical solutions of periodic flows and chaos in nonlinear dynamical systems.

3.1.1 Autonomous Nonlinear Systems

Periodic flows in autonomous dynamical systems will be presented herein. If an autonomous nonlinear system has a periodic flow with period $c03-math-0001$ , then such a periodic flow can be expressed by a generalized coordinate transformation based on the Fourier series. The method is stated through the following theorem.

Theorem 3.1

Consider a nonlinear dynamical system as

3.1 $c03-math-0002$

where $c03-math-0003$ is a $c03-math-0004$ -continuous nonlinear function vector ( $c03-math-0005$ ). If such a dynamical system has a periodic flow $c03-math-0006$ with finite norm $c03-math-0007$ and period $c03-math-0008$ , there is a generalized coordinate transformation with $c03-math-0009$ for the periodic flow of Equation (3.1) in a form of

3.2 $c03-math-0010$

with

3.3 $c03-math-0011$

and

3.4 $c03-math-0012$

For $c03-math-0013$ with a prescribed small positive $c03-math-0014$ , the infinite term transformation of the periodic flow $c03-math-0015$ of Equation (3.1), given by Equation (3.2), can be approximated by a finite term transformation $c03-math-0016$ as

3.5 $c03-math-0017$

and the generalized coordinates are determined by

3.6 $c03-math-0018$

where

3.7

and

3.8

Equation (3.6) becomes

3.9

where

3.10

If equilibrium $c03-math-0023$ of Equation (3.6) (i.e., $c03-math-0024$ ) exists, then the approximate solution of periodic flow exists as in Equation (3.5). In vicinity of equilibrium $c03-math-0025$ , with $c03-math-0026$ , the linearized equation of Equation (3.4) is

3.11

and the eigenvalue analysis of equilibrium $c03-math-0028$ is given by

3.12

where $c03-math-0030$ . Thus, the stability and bifurcation of periodic flow can be classified by the eigenvalues of $c03-math-0031$ with

3.13

where $c03-math-0033$ is the total number of negative real eigenvalues, $c03-math-0034$ is the total number of positive real eigenvalues, $c03-math-0035$ is the total number of zero real eigenvalues; $c03-math-0036$ is the total pair number of complex eigenvalues with negative real parts, $c03-math-0037$ is the total pair number of complex eigenvalues with positive real parts, $c03-math-0038$ is the total pair number of complex eigenvalues with zero real parts.

If all eigenvalues of the equilibrium possess negative real parts, the approximate periodic solution is stable.
If at least one eigenvalue of the equilibrium possesses positive real part, the approximate periodic solution is unstable.
The boundaries between stable and unstable equilibriums with higher order singularity give bifurcation and stability conditions with higher order singularity.

Proof

The proof is similar to Luo (2012a). If $c03-math-0039$ is a $c03-math-0040$ -continuous nonlinear function vector ( $c03-math-0041$ ), then the velocity $c03-math-0042$ should be $c03-math-0043$ -continuous ( $c03-math-0044$ ), and the acceleration $c03-math-0045$ should be bounded (i.e., $c03-math-0046$ ). From Equation (3.2), the norms of the periodic flows are defined by

where

Because the periodic flow in Equation (3.1) is bounded (i.e., $c03-math-0049$ ), we have

Thus, the Fourier series transformation of periodic flow as in Equation (3.2) is convergent. From Equation (3.3), using Equations (3.2) and (3.4) gives

For the prescribed small positive $c03-math-0052$ , if $c03-math-0053$ exists, then we have

Therefore, the convergent infinite term transformation in Equation (3.2) can be approximated by a finite term transformation in Equation (3.5) in the sense of $c03-math-0055$ .

Taking the derivative of Equation (3.5) with respect to time generates

Substitution of the foregoing equation into the nonlinear system in Equation (3.1), and application of the virtual work principle for a basis of constant, $c03-math-0057$ and $c03-math-0058$ $c03-math-0059$ as a set of virtual displacements gives

Under $c03-math-0061$ with continuity $c03-math-0062$ (constant) and small $c03-math-0063$ , for $c03-math-0064$ , the foregoing equation gives

where $c03-math-0066$ and $c03-math-0067$ with small $c03-math-0068$ . The foregoing equation generates

where for $c03-math-0070$

and for $c03-math-0072$

Rearranging the foregoing equation gives Equation (3.6), that is,

Introduce

The equation in Equation (3.6) becomes

Consider equilibriums of the foregoing equation (i.e., $c03-math-0077$ ) by

Thus, the solutions of the forgoing equation are the existence conditions of the periodic solutions for the nonlinear dynamical systems. The foregoing equation gives equilibrium $c03-math-0079$ . In vicinity of $c03-math-0080$ , with $c03-math-0081$ , the linearized equation of $c03-math-0082$ is

and the eigenvalue analysis of equilibrium $c03-math-0084$ is completed via

where

Therefore, as discussed before, the eigenvalues of $c03-math-0087$ are classified by

From the stability and bifurcation theory of dynamical systems at equilibrium, the stability, and bifurcation of the periodic solutions can be classified as stated in the theorem. This theorem is proved.

If the Hopf bifurcation of equilibriums of Equation (3.6) occurs, there is a periodic solution of generalized coordinates in Equation (3.5) with a frequency $c03-math-0089$ . Thus, the periodic solution of the generalized coordinates can be expressed as a new generalized coordinate transformation with $c03-math-0090$

3.14

Substitution of Equation (3.14) into Equation (3.5) yields

3.15

If the new solution is still periodic with excitation period $c03-math-0093$ , then for specific $c03-math-0094$ , we have

3.16

For this case, $c03-math-0096$ should be inserted because $c03-math-0097$ terms are already included in the Fourier series expression. Thus,

3.17

For $c03-math-0099$ , the period-1 flow is obtained, and Equation (3.15) will become Equation (3.5). For the period-m flow, we have a new generalized coordinate transformation as

3.18

If $c03-math-0101$ with a prescribed small $c03-math-0102$ , the solution of period-m flow in Equation (3.18) can be approximated by a finite term transformation as

3.19

If $c03-math-0104$ for any $c03-math-0105$ and $c03-math-0106$ , the solution will be quasi-periodic or chaotic instead of periodic. Herein, this case will not be discussed. If period-1 motion possesses at least $c03-math-0107$ harmonic vector terms, then the total harmonic vector terms for period-m flow should be $c03-math-0108$ . Similarly, the period-m flows in nonlinear dynamical systems can be discussed.

Theorem 3.2

Consider a nonlinear dynamical system in Equation (3.1). If such a dynamical system has a period-m flow $c03-math-0109$ with finite norm $c03-math-0110$ and period $c03-math-0111$ , there is a generalized coordinate transformation with $c03-math-0112$ for the period-m flow of Equation (3.1) in the form of

3.20 $c03-math-0113$

with

3.21

and

3.22 $c03-math-0115$

For $c03-math-0116$ with a prescribed small $c03-math-0117$ , the infinite term transformation $c03-math-0118$ of the period-m flow of Equation (3.1), given by Equation (3.20), can be approximated by a finite term transformation $c03-math-0119$ as

3.23 $c03-math-0120$

and the generalized coordinates are determined by

3.24 $c03-math-0121$

where

3.25

and

3.26

Equation (3.24) becomes

3.27 $c03-math-0124$

where

3.28

If equilibrium $c03-math-0126$ of Equation (3.27) (i.e., $c03-math-0127$ ) exists, then the approximate solution of period-m flow exists as in Equation (3.23). In vicinity of equilibrium $c03-math-0128$ , with $c03-math-0129$ , the linearized equation of Equation (3.27) is

3.29

and the eigenvalue analysis of equilibrium $c03-math-0131$ is given by

3.30

where $c03-math-0133$ . The stability and bifurcation of such a period-m flow can be classified by the eigenvalues of $c03-math-0134$ with

3.31

where $c03-math-0136$ is the total number of negative real eigenvalues, $c03-math-0137$ is the total number of positive real eigenvalues, $c03-math-0138$ is the total number of zero real eigenvalues; $c03-math-0139$ is the total pair number of complex eigenvalues with negative real parts, $c03-math-0140$ is the total pair number of complex eigenvalues with positive real parts, $c03-math-0141$ is the total pair number of complex eigenvalues with zero real parts.

1. If all eigenvalues of the equilibrium possess negative real parts, the approximate periodic solution is stable.
If at least one eigenvalue of the equilibrium possesses positive real part, the approximate periodic solution is unstable.
The boundaries between stable and unstable equilibriums with higher order singularity give bifurcation and stability conditions with higher order singularity.

Proof

The proof is similar to Luo (2012a). Since $c03-math-0142$ is a $c03-math-0143$ -continuous nonlinear function vector $c03-math-0144$ , the velocity $c03-math-0145$ should be $c03-math-0146$ -continuous $c03-math-0147$ , and then the acceleration $c03-math-0148$ should be bounded (i.e., $c03-math-0149$ ). From Equation (3.20) the norms of the periodic flows are defined by

where

Because the periodic flow in Equation (3.1) is bounded (i.e., $c03-math-0152$ ), we have

Thus, the Fourier series transformation of periodic flow as in Equation (3.1) is convergent. From Equation (3.22), using Equations (3.20) and (3.23) gives

For the prescribed small positive $c03-math-0155$ , if $c03-math-0156$ exists, then

Therefore, the convergent infinite term transformation in Equation (3.20) can be approximated by a finite term transformation in Equation (3.23) in the sense of $c03-math-0158$ .

Taking the derivative of Equation (3.23) with respect to time gives

Substitution of the foregoing equation into the nonlinear system in Equation (3.1) and application of the virtual work principle for a basis of constant, $c03-math-0160$ and $c03-math-0161$ $c03-math-0162$ as a set of virtual displacements gives

Under $c03-math-0164$ with continuity $c03-math-0165$ (constant) and small $c03-math-0166$ , for $c03-math-0167$ , the foregoing equation gives

where $c03-math-0169$ and $c03-math-0170$ with small $c03-math-0171$ . From the foregoing equation, we have

where

$c03-math-0174$ and

Rearranging the foregoing equation gives Equation (3.24), that is,

Introducing

the standard form of equation in Equation (3.24) becomes

Consider the equilibrium solution of the foregoing equation with $c03-math-0179$ (i.e., $c03-math-0180$ ) by

Thus, solutions of the foregoing equation are the existence conditions of periodic solutions for nonlinear dynamical systems. Thus, the foregoing equation gives $c03-math-0182$ . In the vicinity of $c03-math-0183$ , with $c03-math-0184$ the linearized equation of $c03-math-0185$ is

and the eigenvalue analysis of equilibrium $c03-math-0187$ is completed via

where

Thus, the corresponding eigenvalues are classified by

If $c03-math-0191$ , Equation (3.20) will give the analytical expression of chaos in dynamical systems in Equation (3.1), which can be approximated by Equation (3.23) under the condition of $c03-math-0192$ . The route from the periodic flow to chaos is through the Hopf bifurcation.

3.1.2 Non-Autonomous Nonlinear Systems

Periodic flows in periodically excited nonlinear dynamical systems will be presented herein. If a periodically excited nonlinear system with an external period $c03-math-0193$ has a periodic flow, then such a periodic flow can be expressed by a Fourier series. The methodology is presented through the following theorems.

Theorem 3.3

Consider a non-autonomous nonlinear dynamical system as

3.32 $c03-math-0194$

where $c03-math-0195$ is a $c03-math-0196$ -continuous nonlinear function vector $c03-math-0197$ with an excitation period $c03-math-0198$ . If such a dynamical system has a periodic flow $c03-math-0199$ with finite norm $c03-math-0200$ , there is a generalized coordinate transformation with $c03-math-0201$ for the periodic flow of Equation (3.32) in a form of

3.33 $c03-math-0202$

with

3.34

and

3.35

For $c03-math-0205$ with a prescribed small positive $c03-math-0206$ , the infinite term transformation of the periodic flow $c03-math-0207$ of Equation (3.32), given by Equation (3.33), can be approximated by a finite term transformation $c03-math-0208$ as

3.36 $c03-math-0209$

and the generalized coordinates are determined by

3.37 $c03-math-0210$

where

3.38

and for $c03-math-0212$

3.39

Equation (3.37) becomes

3.40 $c03-math-0214$

where

3.41

If equilibrium $c03-math-0216$ of Equation (3.40) (i.e., $c03-math-0217$ ) exists, then the approximate solution of periodic flow exists as in Equation (3.36). In vicinity of equilibrium $c03-math-0218$ , with $c03-math-0219$ the linearized equation of Equation (3.40) is

3.42

and the eigenvalue analysis of equilibrium $c03-math-0221$ is given by

3.43

where $c03-math-0223$ . Thus, the stability and bifurcation of periodic flow can be classified by the eigenvalues of $c03-math-0224$ with

3.44

If all eigenvalues of the equilibrium possess negative real parts, the approximate periodic solution is stable.
2. If at least one of the eigenvalues of the equilibrium possesses positive real part, the approximate periodic solution is unstable.
The boundaries between stable and unstable equilibriums with higher order singularity give bifurcation and stability conditions with higher order singularity.

Because they are similar to the autonomous nonlinear system, period-m flows in the periodically excited, nonlinear dynamical system in Equation (3.32) can be discussed.

Theorem 3.4

Consider an autonomous nonlinear dynamical system in Equation (3.32) with an excitation period $c03-math-0226$ . If such a dynamical system has a period-m flow $c03-math-0227$ with finite norm $c03-math-0228$ , there is a generalized coordinate transformation with $c03-math-0229$ for the periodic flow of Equation (3.32) in the form of

3.45 $c03-math-0230$

with

3.46

and

3.47

For $c03-math-0233$ with a prescribed small $c03-math-0234$ , the infinite term transformation $c03-math-0235$ of the period-m flow of Equation (3.32), given by Equation (3.45), can be approximated by a finite term transformation $c03-math-0236$ as

3.48 $c03-math-0237$

and the generalized coordinates are determined by

3.49 $c03-math-0238$

where for $c03-math-0239$

3.50

and

3.51

Equation (3.49) becomes

3.52 $c03-math-0242$

where

3.53

If equilibrium $c03-math-0244$ of Equation (3.52) (i.e., $c03-math-0245$ ) exists, then the approximate solution of period-m flow exists as in Equation (3.48). In the vicinity of equilibrium $c03-math-0246$ , with $c03-math-0247$ , the linearized equation of Equation (3.52) is

3.54

and the eigenvalue analysis of equilibrium $c03-math-0249$ is given by

3.55

where $c03-math-0251$ . The stability and bifurcation of period-m flow can be classified by the eigenvalues of $c03-math-0252$ with

3.56

If all eigenvalues of the equilibrium possess negative real parts, the approximate periodic solution is stable.
If at least one of the eigenvalues of the equilibrium possesses positive real part, the approximate periodic solution is unstable.
3. The boundaries between stable and unstable equilibriums with higher order singularity give bifurcation and stability conditions with higher order singularity.

If $c03-math-0254$ , Equation (3.45) will give the analytical expression of chaos in periodically excited, nonlinear dynamical systems in Equation (3.32), which can be approximated by Equation (3.48) under the condition of $c03-math-0255$ as $c03-math-0256$ .

3.2 Nonlinear Vibration Systems

In this section, the analytical solutions of periodic motions for nonlinear vibration systems are presented owing to extensive application, and the local stability and bifurcation theory will be applied to determine the stability and bifurcation of approximate solutions of periodic motions in nonlinear vibration systems.

3.2.1 Free Vibration Systems

Periodic motions in nonlinear vibration systems will be presented herein. If such a vibration system has periodic motions with period $c03-math-0257$ , then such periodic motions can be expressed by the Fourier series.

Theorem 3.5

Consider a nonlinear vibration system as

3.57 $c03-math-0258$

where $c03-math-0259$ is a $c03-math-0260$ -continuous nonlinear function vector $c03-math-0261$ . If such a dynamical system has a periodic motion $c03-math-0262$ with finite norm $c03-math-0263$ and period $c03-math-0264$ , there is a generalized coordinate transformation with $c03-math-0265$ for the periodic motion of Equation (3.57) in a form of

3.58 $c03-math-0266$

with

3.59

and

3.60 $c03-math-0268$

For $c03-math-0269$ with a prescribed small positive $c03-math-0270$ , the infinite term transformation of the periodic motion $c03-math-0271$ of Equation (3.57), given by Equation (3.58), can be approximated by a finite term transformation $c03-math-0272$ as

3.61 $c03-math-0273$

and the generalized coordinates are determined by

3.62 $c03-math-0274$

where

3.63

and for $c03-math-0276$

3.64

The state-space form of Equation (3.62) is

3.65 $c03-math-0278$

where

3.66

An equivalent system of Equation (3.65) is

3.67 $c03-math-0280$

where

3.68

If equilibrium $c03-math-0282$ of Equation (3.67) (i.e., $c03-math-0283$ ) exists, then the approximate solution of periodic motion exists as in Equation (3.61). In the vicinity of equilibrium $c03-math-0284$ , with $c03-math-0285$ the linearized equation of Equation (3.67) is

3.69

and the eigenvalue analysis of equilibrium $c03-math-0287$ is given by

3.70

where $c03-math-0289$ . Thus, the stability and bifurcation of periodic motions can be classified by the eigenvalues of $c03-math-0290$ with

3.71 $c03-math-0291$

If all eigenvalues of the equilibrium possess negative real parts, the approximate periodic solution is stable.
If at least one of the eigenvalues of the equilibrium possesses positive real part, the approximate periodic solution is unstable.
The boundaries between stable and unstable equilibriums with higher order singularity give bifurcation and stability conditions with higher order singularity.

Proof

The proof is similar to Luo (2012a). Since $c03-math-0292$ is a $c03-math-0293$ -continuous nonlinear function vector ( $c03-math-0294$ ), the velocity $c03-math-0295$ should be $c03-math-0296$ -continuous $c03-math-0297$ , and then the acceleration $c03-math-0298$ should be bounded (i.e., $c03-math-0299$ ). From Equation (3.58), the norms of the periodic motion are defined by

where

Because the periodic motion in Equation (3.57) is bounded (i.e., $c03-math-0302$ ), we have

Thus, the Fourier series transformation of periodic motion as in Equation (3.58) is convergent. From Equation (3.60), using Equations (3.58) and (3.61) gives

For the prescribed small positive $c03-math-0305$ , if $c03-math-0306$ exist, then we have

Therefore, the convergent infinite term transformation in Equation (3.58) can be approximated by a finite term transformation in Equation (3.61) in a sense of $c03-math-0308$ .

Taking the derivative of Equation (3.61) with respect to time gives

Substitution of the foregoing equation into Equation (3.57), and application of the virtual work principle for constant, $c03-math-0310$ and $c03-math-0311$ ( $c03-math-0312$ ) as a set of virtual displacements gives,

Under $c03-math-0314$ with continuity $c03-math-0315$ (constant) and small $c03-math-0316$ , for $c03-math-0317$ , the foregoing equation gives,

where $c03-math-0319$ with $c03-math-0320$ $c03-math-0321$ for small $c03-math-0322$ . The foregoing equation generates,

where

Introduce

Rearranging the foregoing equation gives Equation (3.62), that is,

Let

The equation in Equation (3.62) becomes

Letting $c03-math-0329$ and $c03-math-0330$ , we have

Consider the equilibrium solution of the foregoing equation (i.e., $c03-math-0332$ ), that is,

Thus, the solutions of the foregoing equation are the existence conditions of the periodic solutions for nonlinear vibration systems. If the foregoing equation gives the equilibrium $c03-math-0334$ . In vicinity of $c03-math-0335$ , with $c03-math-0336$ , the linearized equation of $c03-math-0337$ is

and the eigenvalue analysis of equilibrium $c03-math-0339$ is given by

where

Thus, the stability and bifurcation of periodic solution can be classified by the eigenvalues of Equation (3.71) at equilibrium $c03-math-0342$ with

If the Hopf bifurcation of equilibriums of Equation (3.67) occurs, there is a periodic solution of coefficients in Equation (3.62) with a frequency $c03-math-0344$ . As discussed from Equation (3.14) to Equation (3.19), there is a period-m motion as in Equation (3.18). If $c03-math-0345$ for any $c03-math-0346$ and $c03-math-0347$ , the solution will be quasi-periodic or chaotic instead of periodic. Herein, the period-m motions in vibration systems will be discussed only.