3
Risks and Benefits: Game-Theoretical Analysis and Algorithm for Virtual Machine Security Management in the Cloud
Luke Kwiat1, Charles A. Kamhoua2, Kevin A. Kwiat3, and Jian Tang4
1Department of Industrial and Systems Engineering, University of Florida, Gainesville, FL, USA
2Network Security Branch, Network Sciences Division, U.S. Army Research Laboratory, Adelphi, MD, USA
3Haloed Sun TEK, Sarasota, FL, USA
4Department of Electrical Engineering and Computer Science, Syracuse University, Syracuse, NY, USA
The growth of cloud computing has spurred many entities, both small and large, to use cloud services in order to achieve cost savings. Public cloud computing has allowed for quick, dynamic scalability without much overhead or long-term commitments. However, there are some disincentives to using cloud services, and one of the biggest is the inherent and unknown danger stemming from a shared platform – namely, the hypervisor. An attacker who compromises a virtual machine (VM) and then goes on to compromise the hypervisor can readily compromise all virtual machines on that hypervisor. That brings into play the game-theoretic problem of negative externalities, in which the security of one player affects the security of another. Using game theory to model and solve these externalities, we show that there are multiple Nash equilibriums. Furthermore, we demonstrate that the VM allocation type can adversely affect the role that externality plays in the cloud security game. Finally, we propose an allocation method based on a Nash equilibrium such that the negative externality imposed on other players can be significantly lowered compared to that found with other common VM allocation methods.
3.1 Introduction
Cloud computing is rapidly becoming a standard resource in the IT field. It has been predicted that “by 2017, nearly two-thirds of all workloads will be processed in the cloud,” and that cloud traffic would grow by 370% from 2012 to 2017 [1]. Given such astounding growth, it is becoming exceedingly challenging for security to keep pace, especially since demand for security is often overlooked by clients in favor of performance and reliability. Security is difficult to quantify and offers less tangible obvious benefits than performance or other cost-cutting measures, but even so, there are very apparent issues with cloud security. Security-sensitive companies are fearful of the possible theft of confidential or other sensitive data, and that fear poses a “significant barrier to the adoption of cloud services” [2].
The argument that current security measures in the cloud are insufficient has significant merit. Many cloud providers are unaware of the extent of their own security vulnerabilities, and this issue is compounded by the unique structure of the cloud. Many different users run virtual machines (VMs) on the same physical hardware, and that can allow an attacker to distribute his or her attack throughout the hypervisor and onto all the VMs running on that hypervisor. Under those conditions, one user's VM may be indirectly attacked when a direct attack is launched on a different user's VM on the same hypervisor. That is possible because the hypervisor may have unknown security vulnerabilities that, once compromised, can allow an attacker to permeate every VM on the targeted hypervisor [3]. This phenomenon is not common in traditional networks, in which an attacker must use a multihop method to attack victims indirectly. Thus, the problem of interdependency between users on the same hypervisor presents cloud computing providers with a unique challenge: How can virtual machines be allocated for optimum security?
In the cloud, an attacker can launch an indirect attack on User j by first compromising the VMs of User i, successfully attacking the hypervisor and then compromising the VMs of User j. That possibility creates a risk phenomenon wherein the security of User j is dependent on that of User i and vice versa. Further, the problem acquires another dimension if there is a large difference between the potential total losses that could be realized by Users i and j. As a result, big-name users could be discouraged from using the cloud by their much greater potential for loss. With only 56% of cloud users saying they trust cloud providers with sensitive information, and an even smaller 30% stating that they know what procedures cloud providers use for security, the problem is still prevalent [4]. Because of the interacting and interdependent nature of cloud users, we may use game theory to find solutions by modeling those users' choices, since game theory offers “mathematical models of conflict and cooperation between intelligent rational decision-makers” [5].
This chapter reviews and summarizes several contributions. Primarily, its focus is on modeling the choices of several rational players in the cloud within a game-theoretical framework. We will describe the externality problem discussed in Ref. [6] and propose how it can be solved through effective VM allocation management by the cloud provider to ensure delivery of maximum security and minimal loss potential for all cloud users. We aim to use the knowledge gained from this model to influence cloud providers to make optimal security-based virtual machine allocation decisions.
Section 3.2 discusses the potential role of cloud technologies, including those detailed in this chapter, in military missions. Section 3.3 describes related prior work and how the work discussed in the remainder of this chapter is different. Section 3.4 elaborates on the cloud architecture that is used in our game model and that is common to many cloud structures. Section 3.5 sets up the game model and diagrams the game in normal (matrix) form. After analyzing the game result for the simplest case in Section 3.6, we will extend our model in Section 3.7. Section 3.8 will present numerical results and compare our model's negative externality to that of other, more commonly used allocation methods. Section 3.9 concludes the chapter with thoughts on future developments.
3.2 Vision: Using Cloud Technology in Missions
In the term cloud computing, the modifier cloud is simply a metaphor for the Internet. Indeed, graphic illustrations of the Internet almost always depict it as an iconic cloud with white semicircles gathered together to form a large, puffy shape. It is a fitting symbol for the Internet because like a cloud, the Internet has the qualities of expansiveness and a seemingly continuously changing conformation. Cloud computing, or Internet-based computing, embraces those qualities. Its expansiveness inheres in its broad network access and abundantly available computing resources for on-demand service, and its continuously changing conformation is evident in its broad resource pooling and the rapid elasticity of those resources. The derived benefits of cloud computing – or simply “the cloud” – include faster deployment, infrastructure flexibility, and freedom from upfront investment. Although it appears amorphous, the cloud offers computing services that are monitored, controlled, and reported.
Unfortunately, another visual image that can be associated with cloud computing is that of a dark cloud that imparts a sense of foreboding. It is applicable because the aforementioned benefits of cloud computing are overshadowed by security risks that stem from cloud computing's openness and sharing of resources. In spite of the presence of monitoring, controls, and reporting, the inherent security risks create justifiable apprehension. Sound security practice dictates that the risks be continually assessed and appropriately mitigated.
In 2007, Air Force General T. Michael Moseley stated that the Air Force's mission is to “deliver sovereign options for the defense of the United States of America and its global interests – to fly and fight in Air, Space, and Cyberspace” [7]. To accomplish its mission, the Air Force takes the fight into the clouds, by which we now mean two types of clouds: not just the atmospheric phenomena but now the computational cloud as well. The forerunners of today's Air Force were the World War I flyers, for whom the air was a new arena for military combat. They realized that their missions should not be restricted to the open air of clear skies; instead, they would have to venture into the clouds (of the first type). This was a risky endeavor not just because of the turbulence they encountered in their rickety, canvas-skinned aircraft but also because the clouds could conceal something harmful within. Eventually techniques were developed to overcome this limitation of airpower. Now, the Air Force has leapt ahead to venture into contemporary clouds (of the second type). Therefore, like the early pioneers of military flight, we must address the attendant cyber risks so that pursuit of the Air Force's mission can continue to reach “into the clouds.”
The cloud metaphor applies to multiple mission environments (i.e., both air and cyberspace), but cloud computing performs a role in the national information infrastructure that creates distinct mission considerations. Historically, a nation's commercial infrastructure can be found at the forefront of its military operations. For example, at the time of the Civil War, railways of the United States had become a key part of the nation's transportation infrastructure. The railways were viewed as so strategically critical for the expeditious movement of troops that in January of 1862, an act was passed authorizing President Lincoln to have the government take possession of important railway lines [8]. Assuming the total control of a public computing cloud in such a manner would be drastic; however, in the military acronym C4I, which stands for “command, control, communications, computers, and intelligence,” the fourth “C” indicates that computation is viewed by the military authorities as critical to meeting strategic requirements. Given this criticality, it is conceivable that in times of urgency, the military might look to commercial resources such as the public cloud; cloud computing's openness has ushered in the prospect of garnering needed military computing resources directly from the public cloud. (Note that the term “public cloud” does not imply government-owned resources; instead, like the railways, it is a privately owned resource that is made available to the public.) The hypothetical commandeering by the military of the public cloud would likely not be done on a permanent basis; instead, following the mission, the resources would be returned to their original public state. At the end of the Civil War, an Executive Order of August 8, 1865 restored the government-controlled railways to their original owners [8]; similarly, when the military's needs in the cloud have been fulfilled, any computing resources it has taken over can be readily released in accordance with the cloud's property of elasticity. The seizure of the railways was done to ensure that they could be used with militarily precise efficiency and regularity. Likewise, complete possession of the cloud would be a significant risk-reducer: If cloud resources are not being shared, the possibility of negative externalities can be eliminated. However, resorting to the heavy-handed action of assuming complete public cloud possession would defeat almost all of the economic advantages offered by cloud computing. Indeed, the public cloud would no longer be “public”; instead, the computing needs of nonmilitary users would be disregarded. The situation would be analogous to one in which military-controlled railways halted all commercial passenger and freight traffic, placing extreme hardship upon civilians. A loss of public cloud services would have a similarly negative impact on the civilian sector. The magnitude of the negative impact could be especially great during postconflict nation-building or humanitarian missions following natural disasters. In such scenarios, the military's exclusive use of the (perhaps fledgling) public cloud could disastrously interfere with the computational needs of the citizens whose country is being rebuilt. Therefore, our goal for the computational cloud should be, as part of a national information infrastructure, to allow unfettered access to both the public and those performing military missions. That is a core tenet of our game-theoretical analysis and algorithm for virtual machine security management in the cloud: It admits the coexistence of nonmilitary users together with users engaged in military missions. Permitting coexistence, however, requires caution, because it can present unacceptable risks to a military mission's virtual machines. Consequently, our virtual machine security management scheme's ability to balance security risks buttresses the public cloud's ability to accommodate military and nonmilitary users simultaneously.
It is not enough that our game-theoretical algorithm for virtual machine security management embraces the principles of coexistence and balanced risk; on top of that, it is of paramount importance that the algorithm's implementation be conducive to public cloud adoption. Our implementation avoids a major pitfall by not taking the form of a military specification (mil-spec). In a previous work [9], we discussed at length the tension between proponents and detractors of mil-specs. In brief, the latter group argues that mil-specs are overburdened with inspection and screening requirements that slow the building of systems to a glacial pace. Use of mil-specs, they contend, has led not to leading-edge, but to trailing-edge designs. We avoid this controversy by not having our algorithm impose specific implementation details on the underlying cloud infrastructure, such as hardware or software applied to individual virtual machines in the form of guards, partitions, or other isolation enforcers. Our algorithm assumes a much greater generality in the cloud's baseline design. That approach makes the public cloud amenable for military use while leaving undisturbed the cloud's inherent properties of openness, broad resource pooling, and rapid elasticity of resources. Preservation of the public cloud's properties will promote its continued development by commercial entities, and those developments can be leveraged to support completion of missions. We view our game-theoretical algorithm for virtual machine security management as one such potential development. From a commercialization perspective, the algorithm provides a lightweight means to lower the cost of allocating cloud computing resources such that the risk associated with so-called “bad neighbors” is ameliorated. One of its advantages is that it offers underprivileged prospective cloud users access that is on par with that of cloud users with more generous security budgets. Increasing the involvement of users from underrepresented classes who seek more affordable computing will expand the overall user base of the cloud, and with an expanding user base, the public cloud will thrive.
If the public cloud is to be a supporting element of C4I, then our game-theoretical algorithm for virtual machine security must keep us on track toward use of cloud technology in missions. We have argued that a public cloud can be a valuable resource for military missions but only if the mission use is done judiciously. Our vision for the game-theoretical algorithm for virtual machine security management is that it will cultivate public cloud growth for military and nonmilitary users alike.
3.3 State of the Art
A major issue in cloud computing is how the cloud provider will allocate the virtual machine instances created by a constant stream of clients. Previous work has looked at many ways to approach the problem. Many of the solutions offered have involved allocation of virtual machines based on load-balancing techniques, energy consumption, or both [10–13].
Wei et al. [11] use game theory in order to maximize the efficiency of resources within a cloud computing environment. Their solution was split into two parts: an independent solution for nonmultiplexing of resource assignments, and a solution that includes multiplexing. The main idea of the problem model is to maximize the utility that is subject to an allocation vector. For the first part of the problem, it was assumed that each task (user) was assigned a specific resource in the cloud and that the subtasks are dependent and communicate with each other. For the independent optimization, only initial strategies (of allocation) are used in computation, and thus an evolutionary game is used for multiple instances. In evolutionary computations, the initial allocation is given, and later ones are calculated using the algorithms given in Ref. [11].
Beloglazov et al. [13] offered several algorithmic solutions rooted in heuristics. A lower utilization threshold was first established, ensuring that if CPU usage below this threshold was encountered, then all the VMs hosted on this server would be migrated elsewhere. For the upper utilization threshold, several algorithms were studied. They included the minimization of migration (MM) policy, which, as stated in its name, served to minimize the amount of VM migrations used to keep the CPU below the upper utilization threshold. The highest potential growth (HPG) policy migrates the VMs that have the lowest usage of the CPU relative to the CPU capacity in order to minimize the potential increase of the host's utilization and prevent a service-level agreement (SLA) violation. Finally, the random choice (RC) policy randomly selects VMs to migrate in order to decrease CPU utilization. After carrying out 10 different tests at different lower utilization thresholds, the authors found that as the lower utilization threshold increased, the SLA violations increased and energy consumption decreased. That gave an optimum lower utilization threshold for each algorithm. Furthermore, out of the three options, it was found that the MM policy was the best policy overall in terms of energy consumption and SLA violation.
Xu and Fortes [10] introduced several algorithms to achieve allocative efficiency such as that described by Beloglazov et al. They used two different research areas to solve the optimization problem: combinatorial (discrete) optimization and multiobjective (fuzzy) optimization. To determine the optimal level of resource management, they suggested a two-level control system, which involves mapping of application workloads and a mapping from virtual resources to physical resources. That gives rise to a local and a global controller. The focus of their paper is on the global controller and its resource mapping problem, which aims to optimize three main variables: the minimization of power usage, the minimization of thermal dissipation, and the minimization of maximum temperature. For the evaluation, six different types of algorithms were pitted against each other, including four offline bin-packing heuristics and two single-objective GGAs (grouping genetic algorithms). The results were measured by performance, robustness, and scalability.
Jalaparti et al. [12] attempted to solve the issue of cloud resource allocation with game theory, much like Wei et al. They used game theory to model the intricate client-to-client and client-to-provider interactions. Thus, they simultaneously solved the cloud provider's problem with allocative efficiency (since allocative procedures today are fairly simplistic and nonoptimal) and allowed the provider to charge near-optimal prices for cloud usage. (Pricing policies are also usually simplistic, with the norm being a fixed pricing model.) The solution is what they called a CRAG (cloud resource allocation game), which was always found to have a Nash equilibrium. They documented the worst case of bounds for the solution (bounds were needed as a result of the price of anarchy, a concept in economics and game theory that measures how the efficiency of a system degrades because of the selfish behavior of its players) and provided several heuristic algorithms that gave near-optimal allocation and pricing policies.
Game theory has also been applied to certain specific aspects of cloud computing, including infrastructure resilience [14], cloud usage pricing [15], and virtual machine allocation [11,12,16].
Han et al. [16] demonstrated a new method of infiltration that can be exploited through the cloud and not through traditional computing: infiltration through side-channels. That threat gives rise to new risks, as attackers can exploit the sharing by users of the hardware used to create VMs. By starting a VM in the same server where a target user has a VM, an attacker can siphon sensitive information from the victim, including Web traffic and even encryption keys. Han et al.'s study uses game theory to find the best method for mitigating such attacks, in which attackers have been shown to have a 40% success rate in colocating VMs with the target user's VM [17]. The setup was a two-player game with an attacker and a defender (the cloud administrator). The defender's utility function was to include weights for power distribution, security, and workload balance of the servers. It was determined that the optimal strategy for each player is a mixed strategy, with each strategy governing a different probability of using a common VM allocation setup used by cloud providers. The relative probabilities of the different VM allocations being played were dependent on several factors, including the lag time used by an attacker to launch a VM.
Rao et al. [14] studied the ability of a cloud computing entity, within the framework of game theory, to provide a given capacity C at a certain probability P given a physical or cyberattack on its infrastructure. A simple game was set up in which a cloud provider with a certain number of servers S was to defend against an attacker attacking these servers. One of the possible ways to mitigate an attack was for the provider to use reinforcement strategies that decreased attacker utility. The formulas for utility included the number of servers, the number of sites, the number of attacked servers, the attacked site, and the distribution of servers across the attacked site. It was concluded through several tests that the survivability of an attack (the ability of the system to operate at capacity C under probability P despite the attack) is heavily influenced by the cost of defense and the cost of attack. If the cost of defense is too high, the provider will choose not to defend the site, and thus the survivability will be 0. Furthermore, if the number of servers that are spread over given sites is changed and the number or the distribution are not made public, then the attacker's utility is diminished, since a linear attack method will not be as effective against a nonlinear setup of servers.
Künsemöller and Karl [15] examined the economics of cloud computing and the viability of its use for a given business. Game theory was specifically used to model a few circumstances in which it would be economically beneficial to use cloud services. In particular, the authors used an extensive-form game that first branched out a decision tree from the cloud provider (based on the different prices the provider would charge for cloud services) and then reached a decision from the potential customer based on that price. The decision for the customer was binary, as he could either use cloud services or build his own data center. The payoff for the provider is clearly maximized if it charges the highest price at which there is a break-even cost-benefit point for the client in using cloud services. Another issue that Künsemöller and Karl addressed was a cloud–data hybrid, in which a client uses a private data center for a base load of information and cloud services during peak demand/hours. A pricelow was used to denote the price at which a complete cloud solution was the best option, and a pricehigh represented the price at which using cloud services in conjunction with a private data center became unviable. Above that highest price for cloud usage, a wholly owned private data center would be the best option for maximum utility. In practice, given the oligopolistic nature of cloud providers, cloud services can be provided with large economies of scale, which can keep the price of cloud services around pricelow. Thus, there are few reasons left for not outsourcing to the cloud.
Outside the areas of game theory and VM allocation, another important effort was that of Ristenpart et al. [17], who pursued discovery of new vulnerabilities in the cloud structure. They looked at the idea of coresident attacks on virtual machines within the cloud network. Unlike any predecessors, they used empirical evidence and actual data from experiments run on the Amazon EC2 cloud. They began by running all five instance types that EC2 offers across three available placement zones within the cloud. From that, they determined that IP assignment was very uniform, in that IP addresses were partitioned by availability zones (most likely in order to make it easy to manage separate network connectivity for these zones). Using that information, the authors developed a test to determine coresidence on network-based technology (and also showed that that type of technology need not be used). Eventually, they showed that an efficient attacker can achieve coresidence in up to 40% of attacks. Once coresidence has been achieved, several methods can be used to extract information from or damage the victim, including measurement of cache usage, launch of denial-of-service or keystroke-timing attacks, theft of cryptographic keys, and estimation of traffic rates. Ristenpart et al. concluded that to ensure unconditional security against cross-VM attacks, it is currently necessary to avoid coresidence.
Kamhoua et al. [6] viewed attacks on the hypervisor and compromise of virtual machines from a game-theoretical perspective. One of the larger issues they presented in Ref. [6], interdependency, is also addressed in this chapter. However, they addressed interdependency mainly as it related to the compromise of one user's security integrity through the lack of investment of another user who is on the same hypervisor, since an attack on the hypervisor may propagate from one user to other users. We touch on that specific scenario in the present chapter, but to a much lesser extent; it is not our main focus here, although we will discuss interdependency in general, and how the choices of some players reflect the relevant payoffs of other players as well. In this chapter, we resolve the negative externality that one player imposes on another as described in Ref. [6]. Our solution is through effective VM allocation management by the cloud provider to ensure delivery of maximum security for all cloud users. That is one of the prominent points of this chapter.
3.4 System Model
Figure 3.1 is the given system model. A public cloud infrastructure that is running on hypervisor H1 has n users, denoted by user U11, U12,…, U1n, each of whom runs a virtual machine, as denoted by VM11, VM12,…, VM1n. Note that the first subscript character is the number of the hypervisor on which the user is located and the second is the user number. For example, the first user operating on hypervisor 3 is U31, and the second user on hypervisor 3 is U32. In addition, we do not make a distinction between the cloud tenant and user. For practical purposes, the tenant is the true entity that manages the VMs as a liaison, while the user in cloud terminology is the end user who hires the tenant and benefits from the cloud (and also the one to realize any ill effects of asset loss). We assume that the cloud tenant will act in good faith (i.e., do what is most secure or best for the end user); thus, the remainder of this chapter will refer to the end user only.

Figure 3.1 System model.
Operating systems that manage the VMs on the cloud are designated (on the first hypervisor) as operating systems OS11,…, OS1n. A single operating system may run multiple applications, which are referred to as Application111,…, Applicationmnk. Each application needs three indices to be represented. The first index shows the hypervisor in which the application is located, the second represents the OS or VM, and the third differentiates the applications run by the same operating system. This setup holds true for all hypervisors, and thus the mth hypervisor will host users Um1, Um2,…, Umn running virtual machines VMm1, VMm2,…, VMmn, and so forth. Each user may run multiple virtual machine instances (and multiple operating systems), but for simplification purposes it will be assumed that each user runs one VM, as it will be shown later that multiple VMs run by one user may be mathematically combined into one VM. The number of applications run by a user will also not impact the model. Thus, the architecture of Figure 3.1 is an accurate simplification and a common structure to the public cloud. Although the physical infrastructures that clouds use will vary (such as different hypervisors, like Xen, VMware, and KVM), the underlying principle of a shared platform in which users are exposed to collateral damage holds true.
Once that model is examined, it becomes evident that there are several issues with the cloud infrastructure. Users who run on the same hypervisor are susceptible to a “bad neighbor” effect, in which an attacker who has compromised one user's VMs may transverse across the hypervisor to launch an attack on another user's VMs on the same hypervisor. That is the problem of interdependency. We hold that if the hypervisor is compromised, then all users located on that hypervisor will be compromised (and suffer the consequences). The reason is that once an attacker has compromised the hypervisor, all VMs hosted on that hypervisor can be freely compromised by the attacker. However, a user who does not have VMs on the particular hypervisor that is being targeted will not suffer the consequences. This observation will play an important role later in this chapter. Next, we will explain and set up the problem in the context of game theory.
3.5 Game Model
We consider four players—an attacker and three users—acting across two hypervisors. We assume that the four players are rational and that they all have an understanding of the system in which the game is played. Furthermore, it is expected that each player can calculate and maximize his or her payoff (i.e., utility). In Section 3.7, we extend the problem to n players and m hypervisors.
Along with those commonly applied game-theoretic assumptions of rationality and common knowledge of the game's space, we further assume that the attacker has three strategies, which involve launching an attack on User 1 (a strategy that we will call A1), on User 2 (A2), or on User 3 (A3). The attacker may directly attack only one user at a time. The strategy used in launching an attack may include steps such as collecting information, compromising credentials, executing an attack payload, establishing a backdoor, and scanning. The strategy for User 2 is binary, since that user's only choices are to invest (I) in security or not to invest (N) in security. In the instance of choosing to invest in security, the user will be allocated to hypervisor 2 (H2), while no investment in security will result in User 2's being allocated to hypervisor 1 (H1). The user who chooses to invest may take multiple courses of action, including updating software, buying new antivirus software, and applying stricter system monitoring. Thus, H2 is the more secure platform for security-conscious cloud users. It is important to note that throughout the remainder of this chapter, we shall refer to users who invest (do not invest) in cloud security and users who are allocated to H2 (H1) interchangeably.
Furthermore, User 1 will automatically be allocated onto H1 (no investment in security), and User 3 will be allocated to H2 (investment in security). In other words, the only user making a choice on whether to invest in security will be User 2. Since User 2 will have two strategies (I or N) and the attacker has three strategies (A1, A2, or A3), there are a total of six possible permutations in the normal-form game, as laid out in Table 3.1.
Table 3.1 Game model in normal form.
| User 2 | |||
| N (H1) | I (H2) | ||
| Attacker | A1 | ||
| A2 | |||
| A3 | |||
The reason for the automatic allocations of User 1 and User 3 is as follows. It is assumed that the relative importance of each user is determined by the total maximum loss that can be suffered by the user if compromised. Those potential total maximum losses are denoted by ![]() , and
, and ![]() , where the subscripts correspond to the user numbers; for example, if User 1's virtual machines were compromised, then User 1 would suffer a loss totaling
, where the subscripts correspond to the user numbers; for example, if User 1's virtual machines were compromised, then User 1 would suffer a loss totaling ![]() . Further, we assume that
. Further, we assume that
This implies that User 3 will suffer the most costly damage (e.g., through loss of information, trade secrets, or client information) if its virtual machines are compromised, and User 1 faces the least amount of damage. Since User 3 faces the biggest potential for loss and User 1 the least, it is logical that User 3 would invest in security (and be allocated to H2) and that User 1 would not invest in security (and be allocated to H1). Thus, the only cloud user making an investment choice in this game will be User 2. The sufficient conditions under which Users 1 and 3 will always be allocated to H1 and H2, respectively, will be shown in the model extension. The strategy profile notation used throughout this chapter will be shown as (attacker strategy, User 2 strategy). For example, the profile of an attacker who attacks User 1 while User 2 invests in security is given as (A1, I).
The probability of a successful attack on an individual user who has invested in security is given as ![]() , where the user has paid cost
, where the user has paid cost ![]() for his or her investment. If a user has not invested in security, then the probability of compromise is
for his or her investment. If a user has not invested in security, then the probability of compromise is ![]() . It is assumed that
. It is assumed that
The reason is that if ![]() , then no logical user would choose to invest in security, since it would not lower his chance of being compromised.
, then no logical user would choose to invest in security, since it would not lower his chance of being compromised.
The probability of a successful attack on a hypervisor after one of its VMs has been compromised is given as ![]() , where we assume
, where we assume
It would be too bold to assume that there is no chance of a successful attack on a hypervisor (![]() ), especially since the current hypervisor security situation is very unclear [3]. On the other hand, not all attacks on the hypervisor are certain to result in a compromise (
), especially since the current hypervisor security situation is very unclear [3]. On the other hand, not all attacks on the hypervisor are certain to result in a compromise (![]() ). Thus, Equation 3.3 results.
). Thus, Equation 3.3 results.
The reward of using cloud services (either security-invested, I, or not security-invested, N) is given as ![]() , which could include monetary savings from the outsourcing of IT or on-demand resources that can dynamically change depending on need.
, which could include monetary savings from the outsourcing of IT or on-demand resources that can dynamically change depending on need.
We turn again to the normal-form game outlined in Table 3.1. The attacker's strategies are represented by rows (and the top mathematical expression of the six game possibilities gives the attacker's payoff). User 2's strategies are shown in the columns (and the bottom six mathematical expressions give the user's payoff). Thus, a game profile of (A1, I) would give the attacker a payoff of ![]() and User 2 a payoff of
and User 2 a payoff of ![]() .
.
The payoffs are calculated as follows, taking strategy profile (A1, I) as an initial example. User 2 will receive reward ![]() from using the cloud services (which is true for all six game possibilities) and will pay expense
from using the cloud services (which is true for all six game possibilities) and will pay expense ![]() , the cost of extra security. Since User 2 is not being attacked directly and is located on a different hypervisor from the one being targeted, the user's expected loss from a successful attack is 0. Thus, the payoff for User 2 is
, the cost of extra security. Since User 2 is not being attacked directly and is located on a different hypervisor from the one being targeted, the user's expected loss from a successful attack is 0. Thus, the payoff for User 2 is ![]() . For the attack targeting User 1, since User 1 has not invested in security, User 1's chance of being compromised is
. For the attack targeting User 1, since User 1 has not invested in security, User 1's chance of being compromised is ![]() . To find the probabilistic loss of User 1, we must multiply the chance of compromise by User 1's total possible loss (
. To find the probabilistic loss of User 1, we must multiply the chance of compromise by User 1's total possible loss (![]() ), which gives an expected loss of
), which gives an expected loss of ![]() . Since User 1 is the only user located on the first hypervisor, the total gain for the attacker who targets User 1 is
. Since User 1 is the only user located on the first hypervisor, the total gain for the attacker who targets User 1 is ![]() .
.
Taking the strategy profile (A1, N) as another example, we can see that the payoff for User 2 is the reward ![]() minus
minus ![]() . The quantity
. The quantity ![]() is the expected loss from a successful compromise of User 2. However, we must multiply that quantity by
is the expected loss from a successful compromise of User 2. However, we must multiply that quantity by ![]() , since User 2 is not a direct target, and in order to compromise User 2, the attacker must first compromise the hypervisor. If User 2 were the main target of the attacker, as seen in strategy profile (A2, N), we can see that User 2's payoff would be the reward
, since User 2 is not a direct target, and in order to compromise User 2, the attacker must first compromise the hypervisor. If User 2 were the main target of the attacker, as seen in strategy profile (A2, N), we can see that User 2's payoff would be the reward ![]() minus the expected loss
minus the expected loss ![]() , that is, without the value
, that is, without the value ![]() , since the attacker need not go through the hypervisor in order to compromise the virtual machines of User 2, because User 2 is a direct target.
, since the attacker need not go through the hypervisor in order to compromise the virtual machines of User 2, because User 2 is a direct target.
When viewing the strategy profile (A2, I) from the attacker's perspective, we can see that his reward is twofold. His payoff from attacking User 2 is ![]() (User 2's expected loss). In addition, the quantity of
(User 2's expected loss). In addition, the quantity of ![]() is added to the attacker's payoff, since User 3 lies on the same hypervisor (H2) as User 2, even though User 3 is not being directly targeted by the attacker. Since User 3 is not a direct target, the attacker must propagate his attack through the hypervisor before he can compromise User 3. As a result, User 3's expected loss is multiplied by
is added to the attacker's payoff, since User 3 lies on the same hypervisor (H2) as User 2, even though User 3 is not being directly targeted by the attacker. Since User 3 is not a direct target, the attacker must propagate his attack through the hypervisor before he can compromise User 3. As a result, User 3's expected loss is multiplied by ![]() (giving
(giving ![]() ), and thus the total payoff for the attacker is
), and thus the total payoff for the attacker is ![]() . Similar methods are used to derive the payoffs for all of the other profiles.
. Similar methods are used to derive the payoffs for all of the other profiles.
3.6 Game Analysis
In this analysis, we seek to find all the Nash equilibria from the game model. In game theory, when the Nash equilibrium profile is reached, no player can improve his or her utility by unilaterally deviating from the result. At that point, no player wants to change his or her strategy, since not changing is the best response given all the other players' actions. Thus, Nash equilibria can predict the behavior of rational agents.
We will begin by analyzing the strategy profiles that are not pure Nash equilibria.
3.7 Model Extension and Discussion
For our model extension, all our previously stated assumptions remain in place, except that the number of users is now increased to n. The number of hypervisors remains at two. In practice, there is a one-to-one mapping of hypervisors to physical servers, so with m hypervisors, cloud clients can pay for increasingly structured levels of security, with H1 being the least secure and Hm being the most secure. The reasoning we applied for two hypervisors is the same for m hypervisors.
A significant issue in Ref. [6] is that an externality (either positive or negative) by one user is imposed upon another. As can be seen in the game analysis in Section 3.6, the mere presence of another player on the same hypervisor allows for collateral damage via attack propagation. In two of the three pure Nash equilibria, User 2 was allocated to the hypervisor that was not being attacked. (In the third Nash conditions stemming from the game analysis in Theorem 3.3, User 2, as the attack's direct target, could not avoid the attack.) These results have very important implications for how we should conduct user allocation in order to attain a maximum level of cloud security.
One of the main results that we can draw from n users is that there is a resultant family of Nash equilibria. We observe the following cases of Nash equilibria, which are similar to the setup of the game model in Section 3.5 but extended to n users:
- Case 1: If
 , then the strategy profile (An, Un−1) is a Nash equilibrium.
, then the strategy profile (An, Un−1) is a Nash equilibrium. - Case 2: If
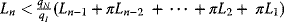 and
and  , then the strategy profile (An−1, Un−1) is a Nash equilibrium.
, then the strategy profile (An−1, Un−1) is a Nash equilibrium. - Subcase 21: If
 ,
, 
 , and
, and  , then the strategy profile (An−2, Un−2) is a Nash equilibrium.
, then the strategy profile (An−2, Un−2) is a Nash equilibrium. - Subcase 22: If
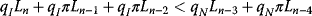
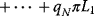 ,
,  , and
, and  , then the strategy profile (An−3, Un−3) is a Nash equilibrium.
, then the strategy profile (An−3, Un−3) is a Nash equilibrium. - Subcase 23: If

 ,
,  , and
, and  , then the strategy profile (An−4, Un−4) is a Nash equilibrium.
, then the strategy profile (An−4, Un−4) is a Nash equilibrium.

- Subcase 2n-1: If

 ,
,  , and
, and  , then the strategy profile (A2, U2) is a Nash equilibrium.
, then the strategy profile (A2, U2) is a Nash equilibrium. - Subcase 2n: If
 ,
,  , and
, and  , then the strategy profile (A1, U1) is a Nash equilibrium.
, then the strategy profile (A1, U1) is a Nash equilibrium.
Case 3: If none of the conditions in Case 1, Case 2, or Case 2 subcases are met, then the game admits a mixed-strategy Nash equilibrium. The goal is to find the user that, when placed on a hypervisor, balances out the total loss on each hypervisor such that the attacker is indifferent as to which hypervisor to target.
Case 1 maps to Theorem 3.1 of the game analysis in Section 3.5. The basic Case 2 is analogous to Theorem 3.2. The final subcase of Case 2 maps to Theorem 3.3, and Case 3 maps to Theorems 3.4 and 3.5. Those results are not unexpected, as the addition of n more users to the original three results in n more pure Nash equilibria, wherein each player has certain conditions that result in that user being targeted by the attacker. In the case of mixed Nash equilibria, we will also see a similar scenario in which each user has the potential to be of particular interest.
For mixed Nash equilibria, among the n users there exists a certain user who alone will make a decision on the hypervisor to which it will allocate itself, that is, all other users will remain static in their allocation choice, regardless of the number of players. That is why User 1 and User 3 were statically placed in H1 and H2, respectively. This placement affirms the observation that there exists only one user who will sit on the threshold of choosing between investing in security and not investing in security, because all other users' expected loss magnitudes balance out. That is, that user is unique: unlike all the other users, this one is unable to choose between invest or not-invest in a binary sense – the reason is that any hypervisor to which the user chooses to allocate itself will be attacked, because the user will “tip” the payoff for the attacker in that direction. Thus, this unique player has a mixed Nash equilibrium, whereas all other players have pure, and static, Nash equilibria.
Since the attacker will always attack the “largest” player in the targeted hypervisor, if the unique user were allocated to hypervisor H1, the unique user would then be the direct victim of an attack, since by default it would be the largest player on H1. The reason is that all players will be grouped by loss potential on the hypervisors, since a small loss gap between players will minimize the externality they impose on each other and thus maximize security. This is a well-studied situation in game theory and is known as Hotelling's law [18]. In accordance with Hotelling's law, players are self-grouping by potential maximum loss. Thus, a situation in which the largest and smallest potential loss players are grouped on one hypervisor, and all of the in-between potential loss players are on another hypervisor, is not observed; rather, players will be allocated with other users with similar total loss potentials.
For a game having n players and with critical User l (1 < l < n), Users 1, 2,…, l − 1 will be located on H1 and Users l + 1, l + 2,…, n − 1, n will be located on H2. If User l chooses to allocate himself to H1, then he will be the direct target of the attack. If he chooses to allocate himself to H2, then User n will be the direct target, and User l merely becomes an indirect target by factor ![]() . Thus, in order for a user to be the pivotal user, the following two equations must be satisfied:
. Thus, in order for a user to be the pivotal user, the following two equations must be satisfied:
and
As can be seen, the pivotal user shifts the inequality and thus the place where the attacker will focus his attack. Note that these equations will hold for ![]() . It is possible that User l + 1 = n or that User l − 1 = 1.
. It is possible that User l + 1 = n or that User l − 1 = 1.
For an example in which n = 5 and all the other variables are defined such that the critical player is n = 3, the two equations will look like
and
VM allocation for User 3 becomes essentially a cat-and-mouse game in which the attacker follows and attacks the hypervisor wherever User 3 goes, since User 3 acts as a pivotal player that tips the equilibrium point just enough that switching the attack methods will result in an increased payoff. Thus, the best strategy for User 3 is not a discrete choice, but rather a mixed strategy, because there is no solution in which both User 3 and the attacker will remain binary in their choices. This phenomenon is not limited to User 3 as a pivotal user. Depending on the various values of ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() , any user from 2 to (n − 1) may be the pivotal user. In Section 3.8.5, in the course of the numerical analysis, we will look at specific values and calculate the pivotal user.
, any user from 2 to (n − 1) may be the pivotal user. In Section 3.8.5, in the course of the numerical analysis, we will look at specific values and calculate the pivotal user.
As previously stated, in our game model, it is assumed that Users 1 and 3 will always be allocated to H1 and H2, respectively. We will now prove the sufficient conditions that will guarantee that the biggest and smallest users will be allocated to opposite hypervisors.
To begin, in order for User 1 always to be allocated to H1 (not investing), its utility from choosing N would always have to be strictly better than that from choosing I. That is shown by the inequality
where the left side of the inequality is User 1's utility from an allocation to H1, and the right side is User 1's utility from an allocation to H2. For User 1, the two utility functions from choosing N or I will always be the same regardless of the attacker's strategy. The reason is that if the end user is making the decision of whether or not to invest (where User 1 is the pivotal user), then all the larger users have already allocated themselves to H2 by investing. It follows that if User 1 were allocated to H2, then H1 would be completely empty of VMs. Thus, the expected loss of User 1 is ![]() since there is no larger user on the first hypervisor to attack, as it is the only user. However, if User 1 chooses to invest and is allocated to H2, then its expected loss includes
since there is no larger user on the first hypervisor to attack, as it is the only user. However, if User 1 chooses to invest and is allocated to H2, then its expected loss includes ![]() , since it will no longer be the largest user located on that hypervisor. (Recall that the attacker will always attack the largest user on its targeted hypervisor, since it is attempting to maximize its utility.) So for User 1 always to be allocated to H1, its utility must always be higher than the utility it would gain from being allocated to H2.
, since it will no longer be the largest user located on that hypervisor. (Recall that the attacker will always attack the largest user on its targeted hypervisor, since it is attempting to maximize its utility.) So for User 1 always to be allocated to H1, its utility must always be higher than the utility it would gain from being allocated to H2.
Continuing to solve the inequality, we show that
Thus, the cost for investment must reach a given threshold to show that User 1 will never invest in security. That conclusion is logical, since if the investment ![]() is high enough, it will dissuade a user from investing. Note that the inequality is only sufficient to prove that User 1 will always choose not to invest.
is high enough, it will dissuade a user from investing. Note that the inequality is only sufficient to prove that User 1 will always choose not to invest.
If we apply similar reasoning to find the utility of User n, we find that it will always be true that User n will be allocated to H2 if the following holds:
Solving for ![]() we discover that
we discover that
That too is logical, since the investment ![]() needs to be low enough such that it encourages the user with the highest possible potential loss always to invest. This investment subsequently gives a total range
needs to be low enough such that it encourages the user with the highest possible potential loss always to invest. This investment subsequently gives a total range ![]() as
as
to show that Users 1 and n will always choose not to invest and to invest, respectively. Since it is assumed in our game model that User 1 and User 3 (n = 3) will always be allocated to their respective hypervisors, we will use condition (3.31) in calculating the allowable range for ![]() in our numerical results.
in our numerical results.
3.8 Numerical Results and Analysis
The following game analysis provides an in-depth explanation of the pure and mixed Nash equilibria. Our key variables in the analysis are ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . We show how User 2's payoff changes with respect to a change in some selected variables.
. We show how User 2's payoff changes with respect to a change in some selected variables.
3.8.1 Changes in User 2's Payoff with Respect to 
In this section we provide specific values for all of the aforementioned constants except ![]() and graph the results. For our first example, we will take
and graph the results. For our first example, we will take ![]() , and
, and ![]() . Applying (3.26), we see that
. Applying (3.26), we see that ![]() , which verifies that
, which verifies that ![]() is an appropriate value. Figure 3.2 shows how the payoff of User 2 changes as
is an appropriate value. Figure 3.2 shows how the payoff of User 2 changes as ![]() increases.
increases.

Figure 3.2 Changes in User 2's payoff with his or her potential loss L2.
The first thing we can immediately see is that there is a strategy change from (A3, N) to a mixed Nash equilibrium at ![]() . The reason is that 1 < L2 < 24.9, the condition for a pure Nash equilibrium (3.7) is satisfied up until 24.9. After that, (7) is falsified; all three conditions of mixed Nash equilibria are fulfilled; and, thus, a strategy change occurs. Notice that as
. The reason is that 1 < L2 < 24.9, the condition for a pure Nash equilibrium (3.7) is satisfied up until 24.9. After that, (7) is falsified; all three conditions of mixed Nash equilibria are fulfilled; and, thus, a strategy change occurs. Notice that as ![]() approaches the value of
approaches the value of ![]() , there is a diminishing payoff from using the cloud, and indeed the payoff turns negative at
, there is a diminishing payoff from using the cloud, and indeed the payoff turns negative at ![]() for the given value of
for the given value of ![]() . The reason is that as
. The reason is that as ![]() increases, α and β decrease and User 2 invests more often. As a result, the increased frequency of direct attacks on User 2 causes User 2's payoff to decrease. The implication of a negative payoff is that after reaching a negative payoff, User 2 will completely opt out of using cloud services.
increases, α and β decrease and User 2 invests more often. As a result, the increased frequency of direct attacks on User 2 causes User 2's payoff to decrease. The implication of a negative payoff is that after reaching a negative payoff, User 2 will completely opt out of using cloud services.
3.8.2 Changes in User 2's Payoff with Respect to 
Moving on to Figure 3.3, we hold all of the same values as before, except we set L2 = 10 and L3 = 20, and graph the applicable value of ![]() with respect to the changing payoff. The reason for the change in variables (
with respect to the changing payoff. The reason for the change in variables (![]() ) is to show the mixed Nash equilibrium and how it changes to pure Nash with increasing
) is to show the mixed Nash equilibrium and how it changes to pure Nash with increasing ![]() .
.

Figure 3.3 Changes in User 2's payoff with expense e.
Too high a value for ![]() will always result in profile (A3, N), so the potential loss values will be more closely clustered in this example. As shown before, the range for e is given in Equation 3.31, which results in
will always result in profile (A3, N), so the potential loss values will be more closely clustered in this example. As shown before, the range for e is given in Equation 3.31, which results in ![]() . That will be our range for the x-axis. We can see a strategy change from a mixed Nash equilibrium to pure Nash at e = 3. One can understand that change intuitively: After that threshold, the choice of investing becomes too expensive and infeasible for User 2, and thus the pure Nash equilibrium (A2, N) results. Note that User 2, despite his or her awareness of being a direct target of the attacker, will not invest in cloud security at this Nash equilibrium. Furthermore, for the selected value of R, User 2 will not use cloud services at all unless there is a low value of e (specifically,
. That will be our range for the x-axis. We can see a strategy change from a mixed Nash equilibrium to pure Nash at e = 3. One can understand that change intuitively: After that threshold, the choice of investing becomes too expensive and infeasible for User 2, and thus the pure Nash equilibrium (A2, N) results. Note that User 2, despite his or her awareness of being a direct target of the attacker, will not invest in cloud security at this Nash equilibrium. Furthermore, for the selected value of R, User 2 will not use cloud services at all unless there is a low value of e (specifically, ![]() ).
).
3.8.3 Changes in User 2's Payoff with Respect to π
Figure 3.4 shows the changing payoff of User 2 as we change the probability of compromising the hypervisor, ![]() . We use the same values as set in the Section 3.8.1 analysis, change
. We use the same values as set in the Section 3.8.1 analysis, change ![]() from a constant to a variable, and set
from a constant to a variable, and set ![]() .
.

Figure 3.4 Changes in User 2's payoff with probability π.
It is apparent that there is no shift in the Nash equilibrium across all values of ![]() . Those results are not surprising, as an increasing
. Those results are not surprising, as an increasing ![]() only slightly increases the externality imposed onto User 2 by other users. The increasing externality problem imposed by an increasing
only slightly increases the externality imposed onto User 2 by other users. The increasing externality problem imposed by an increasing ![]() does not present a significant difference in terms of changing any strategies of the player. That is a very significant discovery since in Ref. [6] there was a Nash equilibrium shift if
does not present a significant difference in terms of changing any strategies of the player. That is a very significant discovery since in Ref. [6] there was a Nash equilibrium shift if ![]() reached a certain threshold, but in this analysis that is not the case, so we have achieved one of the main aims of this research: to reduce the externality imposed onto one user by another. However, it is possible that
reached a certain threshold, but in this analysis that is not the case, so we have achieved one of the main aims of this research: to reduce the externality imposed onto one user by another. However, it is possible that ![]() may shift the Nash equilibrium in exceptional cases in which the conditions for two different Nash equilibria are very close to being met. One instance is that if
may shift the Nash equilibrium in exceptional cases in which the conditions for two different Nash equilibria are very close to being met. One instance is that if ![]() , then
, then ![]() may shift the inequality either way and thus change the Nash equilibrium. In most cases, the Nash equilibrium will not change from the initial conditions, and that is a very positive sign that this security-based allocation will have the effect of mitigating the externality problem.
may shift the inequality either way and thus change the Nash equilibrium. In most cases, the Nash equilibrium will not change from the initial conditions, and that is a very positive sign that this security-based allocation will have the effect of mitigating the externality problem.
It is apparent that a direct attack is very important in deciding where to allocate users. As we will see in the next variable analysis, the ![]() ratio is also very important in determining the prevalent Nash equilibrium.
ratio is also very important in determining the prevalent Nash equilibrium.
3.8.4 Changes in User 2's Payoff with Respect to 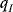
For this section, we will take ![]()
![]() , and
, and ![]() and note that
and note that ![]() was increased to give a greater range of
was increased to give a greater range of ![]() (using
(using ![]() as a variable here). We take
as a variable here). We take ![]() (since
(since ![]() ); the results can be seen in Figure 3.5. For small values of
); the results can be seen in Figure 3.5. For small values of ![]() , the pure Nash profile (A1, I) exists. That makes sense, since if the probability of compromising a VM on the secure hypervisor were so low as to discourage any type of attack, then the attacker would gain a higher payoff by targeting the users who chose not to invest.
, the pure Nash profile (A1, I) exists. That makes sense, since if the probability of compromising a VM on the secure hypervisor were so low as to discourage any type of attack, then the attacker would gain a higher payoff by targeting the users who chose not to invest.

Figure 3.5 Changes in User 2's payoff with probability 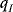 .
.
At ![]() , the Nash equilibrium changes to a mixed strategy and then changes again to the pure Nash equilibrium (A3, N) at
, the Nash equilibrium changes to a mixed strategy and then changes again to the pure Nash equilibrium (A3, N) at ![]() . The second switch of Nash equilibria is feasible since as the
. The second switch of Nash equilibria is feasible since as the ![]() ratio becomes closer to 1, the
ratio becomes closer to 1, the ![]() ratio becomes a more dominant factor in the calculations; at the second threshold, the disparity becomes so large that
ratio becomes a more dominant factor in the calculations; at the second threshold, the disparity becomes so large that ![]() and the switch to strategy profile (A3, N) occurs.
and the switch to strategy profile (A3, N) occurs.
3.8.5 Model Extension to n = 10 Users
In this section, we will continue our model extension and not limit our discussion to just three players. We will take ![]() as before and, per Section 3.7, set the number of users as n = 10. For all of our potential loss values, we will use
as before and, per Section 3.7, set the number of users as n = 10. For all of our potential loss values, we will use ![]()
![]() .
.
Our next step is to find out which of the 10 users is the pivotal user. Thus, we must find the user for which Equations 3.27 and 3.28 are true.
By calculating individual potential losses, we find that User 4 is the pivotal user. This means that
and
which are both true.
Using Equation 3.31, we find that ![]() , which shows that our selected value of
, which shows that our selected value of ![]() is within the restricted range. It is important to note that the value of
is within the restricted range. It is important to note that the value of ![]() will have a strong influence on the prevailing Nash equilibrium. If
will have a strong influence on the prevailing Nash equilibrium. If ![]() then the price for security would be so inexpensive that it would be logical for all users (1–10) to be allocated to H2. If
then the price for security would be so inexpensive that it would be logical for all users (1–10) to be allocated to H2. If ![]() then security would be so expensive that no user would want to invest in security (and, as a result, all would be allocated to H1). Within the allowable range given by (3.31), there are some interesting results. From
then security would be so expensive that no user would want to invest in security (and, as a result, all would be allocated to H1). Within the allowable range given by (3.31), there are some interesting results. From ![]() , there will be a mixed strategy in which User 4 will have a mixed Nash equilibrium while all other users will remain in their respective hypervisors. (U1, U2, and U3 are allocated to H1, while U5, U6, U7, U8, U9, and U10 are allocated to H2). The threshold of 1.56 is determined by the maximum value of e at which User 4 will potentially still pay for security (3.25). Past that point, investing in security will become too expensive, and thus
, there will be a mixed strategy in which User 4 will have a mixed Nash equilibrium while all other users will remain in their respective hypervisors. (U1, U2, and U3 are allocated to H1, while U5, U6, U7, U8, U9, and U10 are allocated to H2). The threshold of 1.56 is determined by the maximum value of e at which User 4 will potentially still pay for security (3.25). Past that point, investing in security will become too expensive, and thus ![]() will result in a pure Nash equilibrium in which U1, U2, U3, and U4 are allocated to H1, while all other users are allocated to H2.
will result in a pure Nash equilibrium in which U1, U2, U3, and U4 are allocated to H1, while all other users are allocated to H2.
To further show the critical role of User 4, in Figure 3.6 we have diagrammed the changing payoff structure for the attacker as the number of users on each hypervisor changes.

Figure 3.6 Change in attacker's payoff with the number of users on the attacked hypervisor.
As can be seen, one line represents the attacker's payoff for attacking H1, and another shows the attacker's payoff for attacking H2. For example, the payoff for the attacker's targeting of H2 if all users are located on H1 is 0. If there is one user on H2 (by default, it would be User 10), then the attacker's payoff is ![]() , which is 1.0. As the number of users on the hypervisor increases, the attacker payoff increases; the attacker payoff will decrease if the number of players decreases.
, which is 1.0. As the number of users on the hypervisor increases, the attacker payoff increases; the attacker payoff will decrease if the number of players decreases.
We can see that the payoffs for each strategy (attacking H1 versus attacking H2) intersect between the abscissa values of 3 and 4 (i.e., there are three or four players on H1, and the remaining players are on H2). However, users take on integer values, so this intersection reflects User 4's status as the pivoting user. At this intersection, the attacker becomes aware of which hypervisor User 4 has been allocated to, since User 4's hypervisor allocation stems from pursuit of a higher payoff. As stated previously, the strategy that U4 chooses will depend on the prevailing value of ![]() . Since
. Since ![]() , we will have a mixed Nash equilibrium.
, we will have a mixed Nash equilibrium.
In Figure 3.7, we show the reduced externality from the mixed-strategy placement of User 4 and the optimum placement of the other users.

Figure 3.7 Externality based on selected allocation types.
The first and second bars represent the total externalities if all users were placed on H1 and H2, respectively, which we calculated by adding all the payoffs of the attacker that contained a factor of ![]() . So the externality of all users on H2 was calculated as the sum of
. So the externality of all users on H2 was calculated as the sum of ![]() . The externality of all users on H1 was calculated similarly. This aggregation of users would be an externality level characteristic of a (fairly standard) allocation method that prioritizes power consumption such that all users are clustered on as few hypervisors as possible.
. The externality of all users on H1 was calculated similarly. This aggregation of users would be an externality level characteristic of a (fairly standard) allocation method that prioritizes power consumption such that all users are clustered on as few hypervisors as possible.
The third bar represents the externality when five VMs are located on H1 and five VMs are located on H2; that scenario is supposed to represent another common allocation method, load balancing. Given our initial conditions, the attacker would attack H1 with probability 1, and thus the externality is calculated as ![]() . With five users on H1, the largest user (U5) will be the direct target, while all the other players will be calculated in the externality figure, since they are all indirect targets.
. With five users on H1, the largest user (U5) will be the direct target, while all the other players will be calculated in the externality figure, since they are all indirect targets.
The fourth bar shows the externality imposed onto other users in the instance of the mixed Nash equilibrium (MNE). The externality from a pure Nash equilibrium ![]() will result in approximately the same value. As can be seen, the negative externality based on a Nash equilibrium allocation is the lowest among the five selected allocation methods, with a 20% externality reduction relative to the second-lowest value (third bar).
will result in approximately the same value. As can be seen, the negative externality based on a Nash equilibrium allocation is the lowest among the five selected allocation methods, with a 20% externality reduction relative to the second-lowest value (third bar).
The fifth bar shows the externality imposed onto other users when random placement, another common VM allocation method, is used. We obtained this value by randomly allocating the VMs between H1 and H2 10 times and averaging the results. This allocation is the second worst for externalities, superior only to placement of all users in the less secure hypervisor, H1. Our proposed allocation method based on mixed-strategy Nash equilibria provides a 56% reduction in externality relative to the random allocation method.
3.9 The Future
The unique properties of a cloud computing structure can allow for new avenues of attack. As stated earlier, the structure of the cloud gives attackers new opportunities to infiltrate and compromise users. Providers of cloud services may attempt to mitigate their vulnerabilities and fend off attempted attacks, but it is an ongoing battle. Many cloud providers may be significantly less secure than they believe, and many more clients are unsuspecting of the potential weaknesses that are inherent in the cloud. One of the issues we presented here was that of externality, whereby one user's lack of security may affect another who has significantly more to lose. While the existence of the externality problem within the context of game theory has been previously shown [6], our earlier publication [19] and this chapter represent the first attainment of a solution. By allowing users to be allocated to hypervisors based on whether or not they have invested in security, we can reduce the negative externality that users can impose on each other. When that type of allocation is used instead of traditional means, such as load balancing or energy optimization, we observe that users will cluster to the same hypervisor as other users based on the most similar loss potentials in order to minimize the negative effects stemming from interdependence. In addition, we have shown that with this type of VM allocation mechanism, there is no significant strategy change with respect to the value of ![]() , giving further proof that the negative externalities are mitigated in this model. The lack of a strategy change holds even at extreme values such as
, giving further proof that the negative externalities are mitigated in this model. The lack of a strategy change holds even at extreme values such as ![]() or
or ![]() . Those findings are supported by the data illustrated in Figure 3.7, which show that our allocation method resulted in the lowest amount of externality by a fair margin.
. Those findings are supported by the data illustrated in Figure 3.7, which show that our allocation method resulted in the lowest amount of externality by a fair margin.
Thus, the Nash equilibrium strategy is more sensitive to initial conditions, such as the potential loss the users face or the cost of investment, than to the externalities. It is apparent that the value of ![]() plays a crucial role in determining the Nash equilibrium, as shown in the numerical results in Section 3.8.5. For cloud providers, that information should be very useful in enabling them to set the value of
plays a crucial role in determining the Nash equilibrium, as shown in the numerical results in Section 3.8.5. For cloud providers, that information should be very useful in enabling them to set the value of ![]() and predetermine the Nash equilibrium best suited for the maximum level of security and minimum externality. For end users, knowledge of the values of π and e can be crucial in helping them decide whether cloud computing is a useful tool that will help them attain cost reductions, or a dubious approach that is fraught with subtle, inherent dangers that have prevented it from proving its worth.
and predetermine the Nash equilibrium best suited for the maximum level of security and minimum externality. For end users, knowledge of the values of π and e can be crucial in helping them decide whether cloud computing is a useful tool that will help them attain cost reductions, or a dubious approach that is fraught with subtle, inherent dangers that have prevented it from proving its worth.
References
- 1 Cisco Systems, Inc. (2013) Cisco Global Cloud Index: forecast and methodology, 2012–2017. Available at https://www.cisco.com/web/mobile/tomorrow-starts-here/files/pdfs/Cisco_CGI_Forecast.pdf.
- 2 Horrigan, J.B., Use of cloud computing applications and services, Pew Internet & American Life Project, Pew Research Center, September 2008. Available at http://www.pewinternet.org/files/old-media//Files/Reports/2008/PIP_Cloud.Memo.pdf.pdf.
- 3 Vaughan-Nichols, S.J., Hypervisors: the cloud's potential security Achilles heel, ZDNet, March 29, 2014. Available at http://www.zdnet.com/article/hypervisors-the-clouds-potential-security-achilles-heel/.
- 4 Thales e-Security, Inc, Thales finds organizations more confident transferring sensitive data to the cloud despite data protection concerns, June 25, 2013. Available at https://www.thales-esecurity.com/company/press/news/2013/june/encryption-in-the-cloud.
- 5 Myerson, R.B. (1997) Game Theory: Analysis of Conflict, Harvard University Press, Cambridge, MA, p. 1.
- 6 Kamhoua, C.A., Kwiat, L., Kwiat, K.A., Park, J.S., Zhao, M., and Rodriguez, M. (2014) Game theoretic modeling of security and interdependency in a public cloud, in Proceedings of the 2014 IEEE 7th International Conference on Cloud Computing (CLOUD), Anchorage, Alaska, pp. 514–521.
- 7 Moseley, T.M., The Nation's Guardians: America's 21st century Air Force, CSAF White Paper, December 29, 2007. Available at http://www.au.af.mil/au/awc/awcgate/af/csaf_white_ppr_29dec07.pdf.
- 8 Carter, E.F. (1964) Railways in Wartime, Frederick Muller Limited, London, UK.
- 9 Kwiat, K. (2001) Can reliability and security be joined reliably and securely? in Proceedings of the 20th IEEE Symposium on Reliable Distributed Systems (SRDS), pp. 72–73.
- 10 Xu, J. and Fortes, J.A.B. (2010) Multi-objective virtual machine placement in virtualized data center environments, in Proceedings of the Green Computing and Communications (GreenCom) and 2010 IEEE/ACM International Conference on Cyber, Physical and Social Computing (CPSCom), Hangzhou, China, pp. 179–188.
- 11 Wei, G., Vasilakos, A.V., Zheng, Y. and Xiong, N. (2010) A game-theoretic method of fair resource allocation for cloud computing services. The Journal of Supercomputing, 54 (2), 252–269.
- 12 Jalaparti, V., Nguyen, G.D., Gupta, I., and Caesar, M., Cloud resource allocation games, University of Illinois at Urbana-Champaign, 2010. Available at http://hdl.handle.net/2142/17427.
- 13 Beloglazov, A. and Buyya, R. (2012) Optimal online deterministic algorithms and adaptive heuristics for energy and performance efficient dynamic consolidation of virtual machines in cloud data centers. Concurrency and Computation: Practice & Experience, 24 (13), 1397–1420.
- 14 Rao, N.S.V., Poole, S.W., He, F., Zhuang, J., Ma, C.Y.T., and Yau, D.K.Y. (2012) Cloud computing infrastructure robustness: a game theory approach, in Proceedings of 2012 International Conference on Computing, Networking and Communications (ICNC), Maui, Hawaii, pp. 34–38.
- 15 Künsemöller, J. and Karl, H. (2012) A game-theoretical approach to the benefits of cloud computing, in Economics of Grids, Clouds, Systems, and Services: GECON 2011 (eds. K. Vanmechelen, J. Altmann, and O.F. Rana), Lecture Notes in Computer Science, vol. 7150, Springer, Heidelberg, Germany, pp. 148–160.
- 16 Han, Y., Alpcan, T., Chan, J., and Leckie, C. (2013) Security games for virtual machine allocation in cloud computing, in Decision and Game Theory for Security: GameSec 2013 (eds. S.K. Das, C. Nita-Rotaru, and M. Kantarcioglu), Lecture Notes in Computer Science, vol. 8252, Springer International Publishing, Switzerland, pp. 99–118.
- 17 Ristenpart, T., Tromer, E., Shacham, H., and Savage, S. (2009) Hey, you, get off of my cloud: exploring information leakage in third-party compute clouds, in Proceedings of the 16th ACM Conference on Computer and Communications Security (CCS '09), Chicago, Illinois, pp. 199–212.
- 18 Hotelling, H. (1929) Stability in competition. The Economic Journal, 39 (153), 41–57.
- 19 Kwiat, L., Kamhoua, C.A., Kwiat, K.A., Tang, J., and Martin, A. (2015) Security-aware virtual machine allocation in the cloud: a game theoretic approach, in Proceedings of the 2015 IEEE 8th International Conference on Cloud Computing (CLOUD), New York, NY, pp. 556–563.
