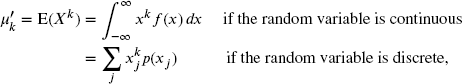3
Basic Distributional Quantities
3.1 Moments
There are a variety of interesting calculations that can be done from the models described in Chapter 2. Examples are the average amount paid on a claim that is subject to a deductible or policy limit or the average remaining lifetime of a person age 40.
Note that 
is not related to 
, the force of mortality from Definition 2.7. For random variables that take on only nonnegative values (i.e. 
), k may be any real number. When presenting formulas for calculating this quantity, a distinction between continuous and discrete variables needs to be made. Formulas will be presented for random variables that are either everywhere continuous or everywhere discrete. For mixed models, evaluate the formula by integrating with respect to its density function wherever the random variable is continuous, and by summing with respect to its probability function wherever the random variable is discrete and adding the results. The formula for the kth raw moment is
where the sum is to be taken over all 
with positive probability. Finally, note that it is possible that the integral or sum will not converge, in which case the moment is said not to exist.
The continuous and discrete formulas for calculating central moments are
In reality, the integral needs be taken only over those x values where 
is positive. The standard deviation is a measure of how much the probability is spread out over the random variable's possible values. It is measured in the same units as the random variable itself. The coefficient of variation measures the spread relative to the mean. The skewness is a measure of asymmetry. A symmetric distribution has a skewness of zero, while a positive skewness indicates that probabilities to the right tend to be assigned to values further from the mean than those to the left. The kurtosis measures flatness of the distribution relative to a normal distribution (which has a kurtosis of 3).2 Kurtosis values above 3 indicate that (keeping the standard deviation constant), relative to a normal distribution, more probability tends to be at points away from the mean than at points near the mean. The coefficients of variation, skewness, and kurtosis are all dimensionless.
There is a link between raw and central moments. The following equation indicates the connection between second moments. The development uses the continuous version from (3.1) and (3.2), but the result applies to all random variables:
Figure 3.1 The densities of 
and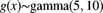 
.
Finally, when calculating moments, it is possible that the integral or sum will not exist (as is the case for the third and fourth moments for Model 2). For the models that we typically encounter, the integrand and summand are nonnegative, and so failure to exist implies that the limit of the integral or sum is infinity. For an illustration, see Example 3.9.
This variable could also be called a left truncated and shifted variable. It is left truncated because any values of X below d are not observed. It is shifted because d is subtracted from the remaining values. When X is a payment variable, the mean excess loss is the expected amount paid, given that there has been a payment in excess of a deductible of d.3 When X is the age at death, the mean excess loss is the expected remaining time until death, given that the person is alive at age d. The kth moment of the excess loss variable is determined from
Here, 
is defined only if the integral or sum converges. There is a particularly convenient formula for calculating the first moment. The development given below is for a continuous random variable, but the result holds for all types of random variables.
The second line is based on an integration by parts, where the antiderivative of 
is taken as 
:
It is left censored because values below d are not ignored but are set equal to zero. There is no standard name or symbol for the moments of this variable. For dollar events, the distinction between the excess loss variable and the left censored and shifted variable is one of per payment versus per loss. In the per-payment situation, the variable exists only when a payment is made. The per-loss variable takes on the value zero whenever a loss produces no payment. The moments can be calculated from
It should be noted that
Figure 3.2 The excess loss variable.
Figure 3.3 A left censored and shifted variable.
These concepts are most easily demonstrated with a discrete random variable.
The next definition provides a complementary variable to the excess loss variable.
This variable could also be called the right censored variable. It is right censored because values above u are set equal to u. An insurance phenomenon that relates to this variable is the existence of a policy limit that sets a maximum on the benefit to be paid. Note that 
. That is, buying one insurance policy with a limit of d and another with a deductible of d is equivalent to buying full coverage. This is illustrated in Figure 3.4.
Figure 3.4 A limit of 100 plus a deductible of 100 equals full coverage.
The most direct formulas for the kth moment of the limited loss variable are
Another interesting formula is derived as follows:
where the second line uses integration by parts. For 
, we have
The corresponding formula for discrete random variables is not particularly interesting. The limited expected value also represents the expected dollar saving per incident when a deductible is imposed. The kth limited moment of many common continuous distributions is presented in Appendix A. Exercise 3.8 asks you to develop a relationship between the three first moments introduced previously.
3.1.1 Exercises
- 3.1 Develop formulas similar to (3.3) for
and 
. - 3.2 Calculate the standard deviation, skewness, and kurtosis for each of the five models. It may help to note that Model 2 is a Pareto distribution and the density function in the continuous part of Model 4 is an exponential distribution. Formulas that may help with calculations for these models appear in Appendix A.
- 3.3 (*) A random variable has a mean and a coefficient of variation of 2. The third raw moment is 136. Determine the skewness.
- 3.4 (*) Determine the skewness of a gamma distribution that has a coefficient of variation of 1.
- 3.5 Determine the mean excess loss function for Models 1–4. Compare the functions for Models 1, 2, and 4.
- 3.6 (*) For two random variables, X and Y,
. Let X have a uniform distribution on the interval from 0 to 100 and let Y have a uniform distribution on the interval from 0 to w. Determine w. - 3.7 (*) A random variable has density function
. Determine 
, the mean excess loss function evaluated at 
. - 3.8 Show that the following relationship holds:
- 3.9 Determine the limited expected value function for Models 1–4. Do this using both (3.8) and (3.10). For Models 1 and 2, also obtain the function using (3.9).
- 3.10 (*) Which of the following statements are true?
- The mean excess loss function for an empirical distribution is continuous.
- The mean excess loss function for an exponential distribution is constant.
- If it exists, the mean excess loss function for a Pareto distribution is decreasing.
- 3.11 (*) Losses have a Pareto distribution with
and 
. Determine the mean excess loss at 10,000. - 3.12 Define a right truncated variable and provide a formula for its kth moment.
- 3.13 (*) The severity distribution of individual claims has pdf
Determine the coefficient of variation.
- 3.14 (*) Claim sizes are for 100, 200, 300, 400, or 500. The true probabilities for these values are 0.05, 0.20, 0.50, 0.20, and 0.05, respectively. Determine the skewness and kurtosis for this distribution.
- 3.15 (*) Losses follow a Pareto distribution with
and 
unspecified. Determine the ratio of the mean excess loss function at 
to the mean excess loss function at 
. - 3.16 (*) A random sample of size 10 has two claims of 400, seven claims of 800, and one claim of 1,600. Determine the empirical skewness coefficient for a single claim.
3.2 Percentiles
One other value of interest that may be derived from the distribution function is the percentile function.4 It is the inverse of the distribution function but, because this quantity is not always well defined, an arbitrary definition must be created.
This quantity is sometimes referred to as a quantile. Generally, the quantile uses values between 0 and 1, while the percentile uses values between 0 and 100. Thus the 70th percentile and the 0.7 quantile are the same. However, regardless of the term used, we will always use decimal values when using subscripts. So it will be 
and never 
. If the distribution function has a value of p for one and only one x value, then the percentile is uniquely defined. In addition, if the distribution function jumps from a value below p to a value above p, then the percentile is at the location of the jump. The only time the percentile is not uniquely defined is when the distribution function is constant at a value of p over a range of values of the random variable. In that case, any value in that range (including both endpoints) can be used as the percentile.
Figure 3.5 The percentiles for Model 1.
Figure 3.6 The percentiles for Model 3.
3.2.1 Exercises
- 3.17 (*) The cdf of a random variable is
. Determine the mean, median, and mode of this random variable. - 3.18 Determine the 50th and 80th percentiles for Models 2, 4, and 5.
- 3.19 (*) Losses have a Pareto distribution with parameters
and 
. The 10th percentile is 
. The 90th percentile is 
. Determine the value of 
. - 3.20 (*) Losses have a Weibull distribution with parameters
and 
. The 25th percentile is 1,000 and the 75th percentile is 100,000. Determine the value of 
.
3.3 Generating Functions and Sums of Random Variables
Consider a portfolio of insurance risks covered by insurance policies issued by an insurance company. The total claims paid by the insurance company on all policies are the sum of all payments made by the insurer. Thus, it is useful to be able to determine properties of 
. The first result is a version of the central limit theorem.
When working with a sequence of random variables, there are many types of limit. The limit used in the theorem is called convergence in distribution. It means that for a given argument, the distribution function converges to its limiting case. Here, if we define 
, then, for any value of z, 
, where Z has a standard normal distribution. Thus, probabilities of sums of random variables can often be approximated by those from the normal distribution.
Obtaining the exact distribution or density function of 
is usually very difficult. However, there are a few cases where it is simple. The key to this simplicity is the generating function.
Note that 
and 
. Often, the mgf is used for continuous random variables and the pgf for discrete random variables. For us, the value of these functions is not so much that they generate moments or probabilities but that there is a one-to-one correspondence between a random variable's distribution function and its mgf and pgf (i.e. two random variables with different distribution functions cannot have the same mgf or pgf). The following result aids in working with sums of random variables.
3.3.1 Exercises
- 3.21 (*) A portfolio contains 16 independent risks, each with a gamma distribution with parameters
and 
. Give an expression using the incomplete gamma function for the probability that the sum of the losses exceeds 6,000. Then approximate this probability using the central limit theorem. - 3.22 (*) The severities of individual claims have a Pareto distribution with parameters
and 
. Use the central limit theorem to approximate the probability that the sum of 100 independent claims will exceed 600,000. - 3.23 (*) The severities of individual claims have a gamma distribution (see Appendix A) with parameters
and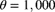 
. Use the central limit theorem to approximate the probability that the sum of 100 independent claims exceeds 525,000. - 3.24 A sample of 1,000 health insurance contracts on adults produced a sample mean of 1,300 for the annual benefits paid with a standard deviation of 400. It is expected that 2,500 contracts will be issued next year. Use the central limit theorem to estimate the probability that benefit payments will be more than 101% of the expected amount.
3.4 Tails of Distributions
The tail of a distribution (more properly, the right tail) is the portion of the distribution corresponding to large values of the random variable. Understanding large possible loss values is important because these have the greatest effect on total losses. Random variables that tend to assign higher probabilities to larger values are said to be heavier tailed. Tail weight can be a relative concept (model A has a heavier tail than model B) or an absolute concept (distributions with a certain property are classified as heavy tailed). When choosing models, tail weight can help narrow the choices or can confirm a choice for a model.
3.4.1 Classification Based on Moments
Recall that in the continuous case, the kth raw moment for a random variable that takes on only positive values (like most insurance payment variables) is given by 
. Depending on the density function and the value of k, this integral may not exist (i.e. it may be infinite). One way of classifying distributions is on the basis of whether all moments exist. It is generally agreed that the existence of all positive moments indicates a (relatively) light right tail, while the existence of only positive moments up to a certain value (or existence of no positive moments at all) indicates a heavy right tail.
By this classification, the Pareto distribution is said to have a heavy tail and the gamma distribution is said to have a light tail. A look at the moment formulas in Appendix A reveals which distributions have heavy tails and which do not, as indicated by the existence of moments.
It is instructive to note that if a distribution does not have all its positive moments, then it does not have a moment generating function (i.e. if X is the associated random variable, then 
for all 
). However, the converse is not true. The lognormal distribution has no moment generating function even though all its positive moments are finite.
Further comparisons of tail behavior can be made on the basis of ratios of moments (assuming they exist). In particular, heavy-tailed behavior is typically associated with large values of quantities such as the coefficient of variation, the skewness, and the kurtosis (see Definition 3.2).
3.4.2 Comparison Based on Limiting Tail Behavior
A commonly used indication that one distribution has a heavier tail than another distribution with the same mean is that the ratio of the two survival functions should diverge to infinity (with the heavier-tailed distribution in the numerator) as the argument becomes large. The divergence implies that the numerator distribution puts significantly more probability on large values. Note that it is equivalent to examine the ratio of density functions. The limit of the ratio will be the same, as can be seen by an application of L'Hôpital's rule:
Figure 3.7 The tails of the gamma and Pareto distributions.
3.4.3 Classification Based on the Hazard Rate Function
The hazard rate function also reveals information about the tail of the distribution. Distributions with decreasing hazard rate functions have heavy tails. Distributions with increasing hazard rate functions have light tails. In the ensuing discussion, we understand “decreasing” to mean “nonincreasing” and “increasing” to mean “nondecreasing.” That is, a decreasing function can be level at times. The exponential distribution, which has a constant hazard rate, is therefore said to have both a decreasing and an increasing hazard rate. For distributions with monotone hazard rates, distributions with exponential tails divide the distributions into heavy-tailed and light-tailed distributions.
Comparisons between distributions can be made on the basis of the rate of increase or decrease of the hazard rate function. For example, a distribution has a lighter tail than another if its hazard rate function is increasing at a faster rate. Often, these comparisons and classifications are of interest primarily in the right tail of the distribution, that is, for large functional values.
3.4.4 Classification Based on the Mean Excess Loss Function
The mean excess loss function also gives information about tail weight. If the mean excess loss function is increasing in d, the distribution is considered to have a heavy tail. If the mean excess loss function is decreasing in d, the distribution is considered to have a light tail. Comparisons between distributions can be made on the basis of whether the mean excess loss function is increasing or decreasing. In particular, a distribution with an increasing mean excess loss function has a heavier tail than a distribution with a decreasing mean excess loss function.
In fact, the mean excess loss function and the hazard rate are closely related in several ways. First, note that
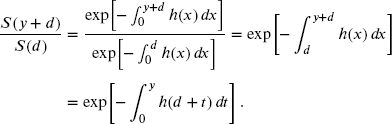
Therefore, if the hazard rate is decreasing, then for fixed y it follows that 
is a decreasing function of d, and from the preceding, 
is an increasing function of d. But from (3.5) the mean excess loss function may be expressed as
Thus, if the hazard rate is a decreasing function, then the mean excess loss function 
is an increasing function of d because the same is true of 
for fixed y. Similarly, if the hazard rate is an increasing function, then the mean excess loss function is a decreasing function. It is worth noting (and is perhaps counterintuitive), however, that the converse implication is not true. Exercise 3.29 gives an example of a distribution that has a decreasing mean excess loss function, but the hazard rate is not increasing for all values. Nevertheless, the implications just described are generally consistent with the preceding discussions of heaviness of the tail.
There is a second relationship between the mean excess loss function and the hazard rate. As 
, 
and 
go to zero. Thus, the limiting behavior of the mean excess loss function as 
may be ascertained using L'Hôpital's rule because formula (3.5) holds. We have
as long as the indicated limits exist. These limiting relationships may be useful if the form of 
is complicated.
3.4.5 Equilibrium Distributions and Tail Behavior
Further insight into the mean excess loss function and the heaviness of the tail may be obtained by introducing the equilibrium distribution (also called the integrated tail distribution). For positive random variables with 
, it follows from Definition 3.3 and (3.5) with 
that 
or, equivalently, 
, so that
is a probability density function. The corresponding survival function is
The hazard rate corresponding to the equilibrium distribution is
using (3.5). Thus, the reciprocal of the mean excess function is itself a hazard rate, and this fact may be used to show that the mean excess function uniquely characterizes the original distribution. We have
or, equivalently,
using 
.
The equilibrium distribution also provides further insight into the relationship between the hazard rate, the mean excess function, and the heaviness of the tail. Assuming that 
, and thus 
, we have 
, and from (3.5), 
. Equating these two expressions results in
If the mean excess function is increasing (which is implied if the hazard rate is decreasing), then 
, which is obviously equivalent to 
from the preceding equality. This, in turn, implies that
But 
from Definition 3.3 and (3.5) if 
. Also,
since both sides represent the mean of the equilibrium distribution. This may be evaluated using (3.9) with 
, and 
to give the equilibrium mean, that is,
The inequality may thus be expressed as
or using 
as 
. That is, the squared coefficient of variation, and hence the coefficient of variation itself, is at least 1 if 
. Reversing the inequalities implies that the coefficient of variation is at most 1 if 
, which is in turn implied if the mean excess function is decreasing or the hazard rate is increasing. These values of the coefficient of variation are consistent with the comments made here about the heaviness of the tail.
3.4.6 Exercises
- 3.25 Using the methods in this section (except for the mean excess loss function), compare the tail weight of the Weibull and inverse Weibull distributions.
- 3.26 Arguments as in Example 3.10 place the lognormal distribution between the gamma and Pareto distributions with regard to heaviness of the tail. To reinforce this conclusion, consider: a gamma distribution with parameters
, 
; a lognormal distribution with parameters 
, 
; and a Pareto distribution with parameters 
, 
. First demonstrate that all three distributions have the same mean and variance. Then, numerically demonstrate that there is a value such that the gamma pdf is smaller than the lognormal and Pareto pdfs for all arguments above that value, and that there is another value such that the lognormal pdf is smaller than the Pareto pdf for all arguments above that value. - 3.27 For a Pareto distribution with
, compare 
to 
and also determine the coefficient of variation. Confirm that these results are consistent with the Pareto distribution being heavy tailed. - 3.28 Let Y be a random variable that has the equilibrium density from (3.11). That is,
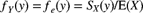for some random variable X. Use integration by parts to show that
whenever
exists. - 3.29 You are given that the random variable X has probability density function
.
- Determine the survival function
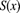. - Determine the hazard rate
. - Determine the survival function
of the equilibrium distribution. - Determine the mean excess function
. - Determine
and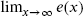 
. - Prove that
is strictly decreasing but 
is not strictly increasing.
- Determine the survival function
- 3.30 Assume that X has probability density function
.
- Prove that
- Use (a) to show that
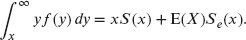
- Prove that (b) may be rewritten as
and that this, in turn, implies that
- Use (c) to prove that, if
, then
and thus
which for
implies that the mean is at least as large as the (smallest) median. - Prove that (b) may be rewritten as
and thus that
- Prove that
3.5 Measures of Risk
3.5.1 Introduction
Probability-based models provide a description of risk exposure. The level of exposure to risk is often described by one number, or perhaps a small set of numbers. These numbers are functions of the model and are often called key risk indicators. Such key risk indicators inform actuaries and other risk managers about the degree to which the company is subject to particular aspects of risk. In particular, Value at Risk (VaR) is a quantile of the distribution of aggregate losses. Risk managers often look at the chance of an adverse outcome. This can be expressed through the VaR at a particular probability level. The VaR can also be used in the determination of the amount of capital required to withstand such adverse outcomes. Investors, regulators, and rating agencies are particularly interested in the company's ability to withstand such events.
The VaR suffers from some undesirable properties. A more informative and more useful measure of risk is Tail Value at Risk (TVaR). It has arisen independently in a variety of areas and has been given different names, including Conditional Value at Risk (CVaR), Average Value at Risk (AVaR), Conditional Tail Expectation (CTE), and Expected Shortfall (ES). See Tasche [119] and Acerbi and Tasche [3].
While these measures have been developed in a risk management context, they are useful in assessing any random variable.
3.5.2 Risk Measures and Coherence
A risk measure is a mapping from the set of random variables representing the loss associated with the risks to the real line (the set of all real numbers). A risk measure gives a single number that is intended to quantify the risk exposure. For example, the standard deviation, or a multiple of the standard deviation of a distribution, is a measure of risk because it provides a measure of uncertainty. It is clearly appropriate when using the normal distribution. In the field of finance, the size of loss for which there is a small (e.g. 0.05%) probability of exceedence is a simple risk measure.
Risk measures are denoted by the function 
. It is convenient to think of 
as the amount of assets required to protect against adverse outcomes of risk X. Studies of risk measures and their properties have included the behavior of risk measures when several losses are combined and treated as a single loss. Combining risks is important in the study of capital needs of an insurance company when considering the overall risk exposure of the insurance company. The insurance company may have several divisions or departments specializing in different products, for example, individual life, homeowners, automobile, group life, annuities, and health. When risk measures are applied to the individual departments, the results should be consistent in some way with the results that are obtained when the risk measure is applied to the entire company. In what follows, it is useful to think of the random variables X and Y as the loss random variables for two divisions and 
as the loss random variable for the entity created by combining the two divisions.
The study of risk measures and their properties has been carried out by numerous authors, such as Wang [126] and [127]. Specific desirable properties of risk measures were proposed as axioms in connection with risk pricing by Wang, Young, and Panjer [128] and more generally in risk measurement by Artzner et al. [7]. The Artzner paper introduced the concept of coherence and is considered to be the groundbreaking paper in risk measurement.
We consider the set of random variables such that if X and Y are two members of the set, then both cX and 
are also in the set. This is not very restrictive, but it does eliminate risks that are measured as percentages, as with Model 1 of Chapter 2.
Subadditivity means that the risk measure (and, hence, the capital required to support it) for two risks combined will not be greater than for the risks treated separately. Subadditivity reflects the fact that there should be some diversification benefit from combining risks. In general, this is necessary at the corporate level. Otherwise, companies would find it to be an advantage to disaggregate into smaller companies. There has been some debate about the appropriateness of the subadditivity requirement. In particular, the merger of several small companies into a larger one exposes each of the small companies to the reputational risk of the others. We will continue to require subadditivity as it reflects the benefit of diversification.
Monotonicity means that if one risk always has greater losses than another risk under all circumstances,5 the risk measure (and, hence, the capital required to support it) should always be greater. This requirement should be self-evident from an economic viewpoint.
Positive homogeneity means that the risk measure (and, hence, the capital required to support it) is independent of the currency in which the risk is measured. Equivalently, it means that, for example, doubling the exposure to a particular risk requires double the capital. This is sensible because doubling the position provides no diversification.
Translation invariance means that there is no additional risk (and, hence, capital required to support it) for an additional risk for which there is no additional uncertainty. In particular, by making X identically zero, the value of the assets required for a certain outcome is exactly the value of that outcome. Also, when a company meets the capital requirement by setting up additional risk-free capital, the act of injecting the additional capital does not, in itself, trigger a further injection (or reduction) of capital.
Risk measures satisfying these four criteria are deemed to be coherent. There are many such risk measures.
In Exercise 3.31, you are asked to prove that the standard deviation principle is not coherent.
If X follows the normal distribution, a value of 
results in an exceedence probability of 
while, if 
, then 
. However, if the distribution is not normal, the same multiples of the standard deviation will lead to different exceedence probabilities. We can also begin with the exceedence probability, obtaining the quantile 
and the equivalent value of k. This is the key idea behind Value at Risk.
3.5.3 Value at Risk
In general terms, Value at Risk (VaR) is the amount of capital required to ensure, with a high degree of certainty, that the enterprise does not become technically insolvent. The degree of certainty chosen is arbitrary. In practice, it can be a high number such as 99.95% for the entire enterprise, or it can be much lower, such as 95%, for a single unit or risk class within the enterprise. This lower percentage may reflect the interunit or interrisk type diversification that exists.
Suppose that 
represents the distribution function of outcomes over a fixed period of time, such as one year, of a portfolio of risks (such as a set of insurance risks or an entire insurance company). An adverse outcome is referred to as a “loss.” In the notation used throughout this book, positive values of the random variable X are adverse outcomes, that is, losses. The VaR of the random variable X is the 100pth percentile of the distribution of X, denoted by 
. This shows why VaR is often called a quantile risk measure. When the insurance company has this amount of capital available, it can absorb 100p% of possible outcomes. When set at 99.95% for a one-year time period, the interpretation is that there is only a very small chance (0.05%) that the insurance company will be bankrupted by an adverse outcome over the next year.
Thus, 
, with equality holding if X is continuous at 
.
For continuous distributions, we can simply write 
for X as the value of 
satisfying
It is well known that VaR does not satisfy one of the four criteria for coherence, the subadditivity requirement. The failure of VaR to be subadditive can be shown by a simple but extreme example inspired by a more complicated one from Wirch [132].
Although this example may appear to be somewhat artificial, the existence of such possibilities creates opportunities for strange or unproductive manipulation. Therefore, we turn to a risk measure that is coherent.
3.5.4 Tail Value at Risk
As a risk measure, VaR is used extensively in financial risk management of trading risk over a fixed (usually relatively short) time period. In these situations, the normal distribution is often used for describing gains or losses. If distributions of gains or losses are restricted to the normal distribution, VaR satisfies all coherency requirements. However, the normal distribution is generally not used for describing insurance losses, which are typically skewed. Consequently, the use of VaR is problematic because of the lack of subadditivity.
It is well known (e.g. Artzner et al. [7]) that TVaR is a coherent risk measure. An alternative formula is (e.g. Embrechts and Wang [35])
If X is continuous at 
, then 
and the formula simplifies to
Furthermore, in this case,
where 
is the mean excess loss function evaluated at the 100pth percentile. Thus TVaR is larger than the corresponding VaR by the average excess of all losses that exceed VaR. Furthermore, because 
, (3.12) expresses 
as a function of 
, and in Exercise 3.37 the fact that 
is a nondecreasing function of 
is established.
Overbeck [96] also discusses VaR and TVaR as risk measures. He argues that VaR is an “all or nothing” risk measure, in that if an extreme event in excess of the VaR threshold occurs, there is no capital to cushion losses. He also argues that the VaR quantile in TVaR provides a definition of “bad times,” which are those where losses exceed the VaR threshold, thereby not using up all available capital when TVaR is used to determine capital. Then, TVaR provides the average excess loss in “bad times,” that is, when the VaR “bad times” threshold has been exceeded.
TVaR is one of many possible coherent risk measures. However, it is particularly well suited to insurance applications where you may want to reflect the shape of the tail beyond the VaR threshold in some way. TVaR represents that shape through a single number: the mean excess loss or expected shortfall.
Table 3.1 The quantiles for Example 3.18.
| Security level | Normal | Pareto | Weibull |
| 0.900 | 386.56 | 226.78 | 265.09 |
| 0.990 | 620.19 | 796.44 | 1,060.38 |
| 0.999 | 791.00 | 2,227.34 | 2,385.85 |
From this example, it should be noted that the results can vary widely depending on the choice of distribution. The normal distribution has a lighter tail than the others. Therefore, the probabilities at extreme outcomes are relatively small, leading to smaller quantiles. The Pareto distribution and the Weibull distribution with 
have heavy tails and thus relatively larger extreme quantiles. This book is devoted to the exercise of selecting the best distribution based on the available information. In the preceding example, knowing only the mean and standard deviation is not enough to estimate the extreme quantiles needed for determining capital requirements.
In practice, obtaining numerical values of VaR or TVaR can be done either from the data directly or from the distributional formulas, as was done in Example 3.18. When estimating VaR from data, the methods of obtaining quantiles from empirical distributions described in Section 10.4.1 can be used. Since TVaR is the expected value of the observations that are larger than a given threshold, the natural estimator is the average of the values of the observations that exceed the threshold. However, we caution against using this approach in practice unless there are a large number of observations in excess of the threshold. In cases where there are not many observations in excess of the threshold, we prefer to obtain a model for the distribution of all of the observations, or at least of all observations in excess of some relatively low threshold. The values of VaR and TVaR can then be calculated directly from the fitted distribution. This can be done easily for the continuous distributions listed in Appendix A using the relation
The 
is defined in Definition 3.5.
3.5.5 Exercises
- 3.31 Prove that the standard deviation principle satisfies coherence criteria 1, 3, and 4. To see that it does not satisfy criterion 2, consider the bivariate variable
that takes on the value (0,4) with probability 0.25 and the value (4,4) with probability 0.75. Using 
, show that monotonicity is not satisfied. - 3.32 Show that the VaR and TVaR formulas in Example 3.16 are correct.
- 3.33 Show that the VaR and TVaR formulas in Example 3.17 are correct.
- 3.34 Verify the parameters and the VaR calculation in Example 3.18
- 3.35 Using (3.13), obtain TVaR at the 99.9% security level for the Weibull(50, 0.5) distribution.
- 3.36 Consider an exponential distribution with
and a Pareto distribution with 
and 
. Determine VaR and TVaR at the 95% security level. - 3.37 Suppose that the distribution of X is continuous on
, where 
(this does not rule out the possibility that 
with discrete mass points at or below 
). For 
, let 
be the pdf, 
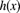be the hazard rate function, and 
be the mean excess loss function. Demonstrate that
and hence that
is nondecreasing in x for 
.