2
Random Variables
2.1 Introduction
An actuarial model is a representation of an uncertain stream of future payments. The uncertainty may be with respect to any or all of occurrence (is there a payment?), timing (when is the payment made?), and severity (how much is paid?). Because the most useful means of representing uncertainty is through probability, we concentrate on probability models. For now, the relevant probability distributions are assumed to be known. The determination of appropriate distributions is covered in Chapters 10 through 15. In this part, the following aspects of actuarial probability models are covered:
- Definition of random variable and important functions, with some examples.
- Basic calculations from probability models.
- Specific probability distributions and their properties.
- More advanced calculations using severity models.
- Models incorporating the possibility of a random number of payments, each of random amount.
The commonality we seek here is that all models for random phenomena have similar elements. For each, there is a set of possible outcomes. The particular outcome that occurs will determine the success of our enterprise. Attaching probabilities to the various outcomes allows us to quantify our expectations and the risk of not meeting them. In this spirit, the underlying random variable will almost always be denoted with uppercase italic letters near the end of the alphabet, such as X or Y. The context will provide a name and some likely characteristics. Of course, there are actuarial models that do not look like those covered here. For example, in life insurance a model office is a list of cells containing policy type, age range, gender, and so on, along with the number of contracts with those characteristics.
To expand on this concept, consider the following definitions from “Principles Underlying Actuarial Science” [5, p. 7]:
Phenomena are occurrences that can be observed. An experiment is an observation of a given phenomenon under specified conditions. The result of an experiment is called an outcome; an event is a set of one or more possible outcomes. A stochastic phenomenon is a phenomenon for which an associated experiment has more than one possible outcome. An event associated with a stochastic phenomenon is said to be contingent. … Probability is a measure of the likelihood of the occurrence of an event, measured on a scale of increasing likelihood from zero to one. … A random variable is a function that assigns a numerical value to every possible outcome.
The following list contains 12 random variables that might be encountered in actuarial work (Model # refers to examples introduced in the next section):
- The age at death of a randomly selected birth. (Model 1)
- The time to death from when insurance was purchased for a randomly selected insured life.
- The time from occurrence of a disabling event to recovery or death for a randomly selected workers compensation claimant.
- The time from the incidence of a randomly selected claim to its being reported to the insurer.
- The time from the reporting of a randomly selected claim to its settlement.
- The number of dollars paid on a randomly selected life insurance claim.
- The number of dollars paid on a randomly selected automobile bodily injury claim. (Model 2)
- The number of automobile bodily injury claims in one year from a randomly selected insured automobile. (Model 3)
- The total dollars in medical malpractice claims paid in one year owing to events at a randomly selected hospital. (Model 4)
- The time to default or prepayment on a randomly selected insured home loan that terminates early.
- The amount of money paid at maturity on a randomly selected high-yield bond.
- The value of a stock index on a specified future date.
Because all of these phenomena can be expressed as random variables, the machinery of probability and mathematical statistics is at our disposal both to create and to analyze models for them. The following paragraphs discuss five key functions used in describing a random variable: cumulative distribution, survival, probability density, probability mass, and hazard rate. They are illustrated with four ongoing models as identified in the preceding list plus one more to be introduced later.
2.2 Key Functions and Four Models
The distribution function must satisfy a number of requirements:2
 for all x.
for all x. is nondecreasing.
is nondecreasing. is right-continuous.3
is right-continuous.3 and
and  .
.
Because it need not be left-continuous, it is possible for the distribution function to jump. When it jumps, the value is assigned to the top of the jump.
Here are possible distribution functions for each of the four models.
Model 14 This random variable could serve as a model for the age at death. All ages between 0 and 100 are possible. While experience suggests that there is an upper bound for human lifetime, models with no upper limit may be useful if they assign extremely low probabilities to extreme ages. This allows the modeler to avoid setting a specific maximum age:
This cdf is illustrated in Figure 2.1.
![]()
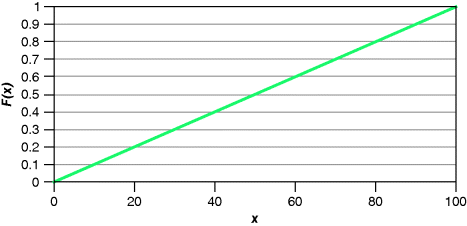
Figure 2.1 The distribution function for Model 1.
Model 2 This random variable could serve as a model for the number of dollars paid on an automobile insurance claim. All positive values are possible. As with mortality, there is likely an upper limit (all the money in the world comes to mind), but this model illustrates that, in modeling, correspondence to reality need not be perfect:
This cdf is illustrated in Figure 2.2.
![]()

Figure 2.2 The distribution function for Model 2.
Model 3 This random variable could serve as a model for the number of claims on one policy in one year. Probability is concentrated at the five points ![]() and the probability at each is given by the size of the jump in the distribution function:
and the probability at each is given by the size of the jump in the distribution function:

While this model places a maximum on the number of claims, models with no limit (such as the Poisson distribution) could also be used.
![]()
Model 4 This random variable could serve as a model for the total dollars paid on a medical malpractice policy in one year. Most of the probability is at zero (0.7) because in most years nothing is paid. The remaining 0.3 of probability is distributed over positive values:
These three definitions do not exhaust all possible random variables but will cover all cases encountered in this book. The distribution function for a discrete random variable will be constant except for jumps at the values with positive probability. A mixed distribution will have at least one jump. Requiring continuous variables to be differentiable allows the variable to have a density function (defined later) at almost all values.
![]()
These four models illustrate the most commonly encountered forms of the distribution function. Often in the remainder of the book, when functions are presented, values outside the support are not given (most commonly where the distribution and survival functions are 0 or 1).
As a result:
 for all x.
for all x. is nonincreasing.
is nonincreasing. is right-continuous.
is right-continuous. and
and  .
.
Because the survival function need not be left-continuous, it is possible for it to jump (down). When it jumps, the value is assigned to the bottom of the jump.
The survival function is the complement of the distribution function, and thus knowledge of one implies knowledge of the other. Historically, when the random variable is measuring time, the survival function is presented, while when it is measuring dollars, the distribution function is presented.
![]()

Figure 2.3 The survival function for Model 1.

Figure 2.4 The survival function for Model 2.
Either the distribution or the survival function can be used to determine probabilities. Let ![]() and let
and let ![]() be similarly defined. That is, we want the limit as x approaches b from below. We have
be similarly defined. That is, we want the limit as x approaches b from below. We have ![]() and
and ![]() . When the distribution function is continuous at x,
. When the distribution function is continuous at x, ![]() ; otherwise, the probability is the size of the jump. The next two functions are more directly related to the probabilities. The first is for continuous distributions, the second for discrete distributions.
; otherwise, the probability is the size of the jump. The next two functions are more directly related to the probabilities. The first is for continuous distributions, the second for discrete distributions.
While the density function does not directly provide probabilities, it does provide relevant information. Values of the random variable in regions with higher density values are more likely to occur than those in regions with lower values. Probabilities for intervals and the distribution and survival functions can be recovered by integration. That is, when the density function is defined over the relevant interval, ![]() ,
, ![]() , and
, and ![]() .
.
![]()

Figure 2.5 The density function for Model 1.

Figure 2.6 The density function for Model 2.
For discrete random variables, the distribution and survival functions can be recovered as ![]() and
and ![]() .
.
![]()
When called the force of mortality, the hazard rate is often denoted ![]() , and when called the failure rate, it is often denoted
, and when called the failure rate, it is often denoted ![]() . Regardless, it may be interpreted as the probability density at x given that the argument will be at least x. We also have
. Regardless, it may be interpreted as the probability density at x given that the argument will be at least x. We also have ![]() . The survival function can be recovered from
. The survival function can be recovered from ![]() . Though not necessary, this formula implies that the support is on nonnegative numbers. In mortality terms, the force of mortality is the annualized probability that a person age x will die in the next instant, expressed as a death rate per year.6 In this text, we always use
. Though not necessary, this formula implies that the support is on nonnegative numbers. In mortality terms, the force of mortality is the annualized probability that a person age x will die in the next instant, expressed as a death rate per year.6 In this text, we always use ![]() to denote the hazard rate, although one of the alternative names may be used.
to denote the hazard rate, although one of the alternative names may be used.
![]()

Figure 2.7 The hazard rate function for Model 1.

Figure 2.8 The hazard rate function for Model 2.
The following model illustrates a situation in which there is a point where the density and hazard rate functions are not defined.
Model 5 An alternative to the simple lifetime distribution in Model 1 is given here. Note that it is piecewise linear and the derivative at 50 is not defined. Therefore, neither the density function nor the hazard rate function is defined at 50. Unlike the mixed model of Model 4, there is no discrete probability mass at this point. Because the probability of 50 occurring is zero, the density or hazard rate at 50 could be arbitrarily defined with no effect on subsequent calculations. In this book, such values are arbitrarily defined so that the function is right-continuous.7 For an example, see the solution to Exercise 2.1.
![]()
A variety of commonly used continuous distributions are presented in Appendix A and many discrete distributions are presented in Appendix B.
An interesting feature of a random variable is the value that is most likely to occur.
![]()
2.2.1 Exercises
- 2.1 Determine the distribution, density, and hazard rate functions for Model 5.
- 2.2 Construct graphs of the distribution function for Models 3, 4, and 5. Also graph the density or probability function as appropriate and the hazard rate function, where it exists.
- 2.3 (*) A random variable X has density function
 ,
,  . Determine the mode of X.
. Determine the mode of X. - 2.4 (*) A nonnegative random variable has a hazard rate function of
 . You are also given
. You are also given  . Determine the value of A.
. Determine the value of A. - 2.5 (*) X has a Pareto distribution with parameters
 and
and  . Y has a Burr distribution with parameters
. Y has a Burr distribution with parameters  ,
, 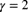 , and
, and  . Let r be the ratio of
. Let r be the ratio of  to
to  . Determine
. Determine  .
.
