15
Model Selection
15.1 Introduction
When using data to build a model, the process must end with the announcement of a “winner.” While qualifications, limitations, caveats, and other attempts to escape full responsibility are appropriate, and often necessary, a commitment to a solution is often required. In this chapter, we look at a variety of ways to evaluate a model and compare competing models. But we must also remember that whatever model we select, it is only an approximation of reality. This observation is reflected in the following modeler's motto:
All models are wrong, but some models are useful.1
Thus, our goal is to determine a model that is good enough to use to answer the question. The challenge here is that the definition of “good enough” will depend on the particular application. Another important modeling point is that a solid understanding of the question will guide you to the answer. The following quote from John Tukey [122 pp. 13–14] sums up this point:
Far better an approximate answer to the right question, which is often vague, than an exact answer to the wrong question, which can always be made precise.
In this chapter, a specific modeling strategy is considered. Our preference is to have a single approach that can be used for any probabilistic modeling situation. A consequence is that for any particular modeling situation, there may be a better (more reliable or more accurate) approach. For example, while maximum likelihood is a good estimation method for most settings, it may not be the best2 for certain distributions. A literature search will turn up methods that have been optimized for specific distributions, but they are not mentioned here. Similarly, many of the hypothesis tests used here give approximate results. For specific cases, better approximations, or maybe even exact results, are available. They are also bypassed. The goal here is to outline a method that will give reasonable answers most of the time and be adaptable to a variety of situations.
This chapter assumes that you have a basic understanding of mathematical statistics as reviewed in Chapters 10 and 11. The remaining sections cover a variety of evaluation and selection tools. Each tool has its own strengths and weaknesses, and it is possible for different tools to lead to different models, making modeling as much art as science. At times, in real-world applications, the model's purpose may lead the analyst to favor one tool over another.
15.2 Representations of the Data and Model
All the approaches to be presented compare the proposed model to the data or to another model. The proposed model is represented by either its density or distribution function, or perhaps some functional of these quantities such as the limited expected value function or the mean excess loss function. The data can be represented by the empirical distribution function or a histogram. The graphs are easy to construct when there is individual, complete data. When there is grouping or observations have been truncated or censored, difficulties arise. Here, the only cases covered are those where the data are all truncated at the same value (which could be zero) and are all censored at the same value (which could be infinity). Extensions to the case of multiple truncation or censoring points are detailed in Klugman and Rioux [75].3 It should be noted that the need for such representations applies only to continuous models. For discrete data, issues of censoring, truncation, and grouping rarely apply. The data can easily be represented by the relative or cumulative frequencies at each possible observation.
With regard to representing the data, the empirical distribution function is used for individual data and the histogram will be used for grouped data.
To compare the model to truncated data, we begin by noting that the empirical distribution begins at the truncation point and represents conditional values (i.e. they are the distribution and density function given that the observation exceeds the truncation point). To make a comparison to the empirical values, the model must also be truncated. Let the truncation point in the data set be t. The modified functions are
and
In this chapter, when a distribution function or density function is indicated, a subscript equal to the sample size indicates that it is the empirical model (from Kaplan–Meier, Nelson–Åalen, the ogive, etc.), while no adornment or the use of an asterisk (*) indicates the estimated parametric model. There is no notation for the true, underlying distribution because it is unknown and unknowable.
15.3 Graphical Comparison of the Density and Distribution Functions
The most direct way to see how well the model and data match is to plot the respective density and distribution functions.
When the model's distribution function is close to the empirical distribution function, it is difficult to make small distinctions. Among the many ways to amplify those distinctions, two are presented here. The first is to simply plot the difference of the two functions. That is, if 
is the empirical distribution function and 
is the model distribution function, plot 
. There is no corresponding plot for grouped data.
Figure 15.5 The model versus data 
plot for Data Set B censored at 1,000.
Another way to highlight any differences is the p–p plot, which is also called a probability plot. The plot is created by ordering the observations as 
. A point is then plotted corresponding to each value. The coordinates to plot are 
. If the model fits well, the plotted points will be near the 45° line running from (0,0) to (1,1). However, for this to be the case, a different definition of the empirical distribution function is needed. It can be shown that the expected value of 
is 
and, therefore, the empirical distribution should be that value and not the usual 
. If two observations have the same value, either plot both points (they would have the same “y” value but different “x” values) or plot a single value by averaging the two “x” values.
15.3.1 Exercises
- 15.1 Repeat Example 15.1 using a Weibull model in place of the exponential model.
- 15.2 Repeat Example 15.2 for a Weibull model.
- 15.3 Repeat Example 15.3 for a Weibull model.
15.4 Hypothesis Tests
A picture may be worth many words, but sometimes it is best to replace the impressions conveyed by pictures with mathematical demonstrations.4 One such demonstration is a test of the following hypotheses:
The test statistic is usually a measure of how close the model distribution function is to the empirical distribution function. When the null hypothesis completely specifies the model (e.g. an exponential distribution with mean 100), critical values are well known. However, it is more often the case that the null hypothesis states the name of the model but not its parameters. When the parameters are estimated from the data, the test statistic tends to be smaller than it would have been had the parameter values been prespecified. This relationship occurs because the estimation method itself tries to choose parameters that produce a distribution that is close to the data. When parameters are estimated from data, the tests become approximate. Because rejection of the null hypothesis occurs for large values of the test statistic, the approximation tends to increase the probability of a Type II error (declaring that the model is acceptable when it is not) while lowering the probability of a Type I error (rejecting an acceptable model).5 For actuarial modeling, this tendency is likely to be an acceptable trade-off.
One method of avoiding the approximation is to randomly divide the sample into two sets. One is termed the training set. This set is used to estimate the parameters. The other set is called the test or validation set. This set is used to evaluate the quality of the model fit. This is more realistic because the model is being validated against new data. This approach is easier to do when there is a lot of data so that both sets are large enough to give useful results. These methods will not be discussed further in this text: for more details, see James et al. [61].
15.4.1 The Kolmogorov–Smirnov Test
Let t be the left truncation point (
if there is no truncation) and let u be the right censoring point (
if there is no censoring). Then, the test statistic is
This test as presented here should only be used on individual data to ensure that the step function 
is well defined.6 Also, the model distribution function 
is assumed to be continuous over the relevant range.
Table 15.4 The calculation of D with censoring for Example 15.4.
| x |  |
 |
 |
Maximum difference |
| 27 | 0.0369 | 0.00 | 0.05 | 0.0369 |
| 82 | 0.1079 | 0.05 | 0.10 | 0.0579 |
| 115 | 0.1480 | 0.10 | 0.15 | 0.0480 |
| 126 | 0.1610 | 0.15 | 0.20 | 0.0390 |
| 155 | 0.1942 | 0.20 | 0.25 | 0.0558 |
| 161 | 0.2009 | 0.25 | 0.30 | 0.0991 |
| 243 | 0.2871 | 0.30 | 0.35 | 0.0629 |
| 294 | 0.3360 | 0.35 | 0.40 | 0.0640 |
| 340 | 0.3772 | 0.40 | 0.45 | 0.0728 |
| 384 | 0.4142 | 0.45 | 0.50 | 0.0858 |
| 457 | 0.4709 | 0.50 | 0.55 | 0.0791 |
| 680 | 0.6121 | 0.55 | 0.60 | 0.0621 |
| 855 | 0.6960 | 0.60 | 0.65 | 0.0960 |
| 877 | 0.7052 | 0.65 | 0.70 | 0.0552 |
| 974 | 0.7425 | 0.70 | 0.75 | 0.0425 |
| 1,000 | 0.7516 | 0.75 | 0.75 | 0.0016 |
All that remains is to determine the critical value. Commonly used critical values for this test are 
for 
, 
for 
, and 
for 
. When 
, the critical value should be smaller because there is less opportunity for the difference to become large. Modifications for this phenomenon exist in the literature (see, e.g., Stephens [116], which also includes tables of critical values for specific null distribution models), and one such modification is given in Klugman and Rioux [75] but is not introduced here.
For both this test and the Anderson–Darling test that follows, the critical values are correct only when the null hypothesis completely specifies the model. When the data set is used to estimate parameters for the null hypothesized distribution (as in the example), the correct critical value is smaller. For both tests, the change depends on the particular distribution that is hypothesized and maybe even on the particular true values of the parameters. An indication of how simulation can be used for this situation is presented in Section 19.4.5.
15.4.2 The Anderson–Darling Test
This test is similar to the Kolmogorov–Smirnov test but uses a different measure of the difference between the two distribution functions. The test statistic is
That is, it is a weighted average of the squared differences between the empirical and model distribution functions. Note that when x is close to t or to u, the weights might be very large due to the small value of one of the factors in the denominator. This test statistic tends to place more emphasis on good fit in the tails than in the middle of the distribution. Calculating with this formula appears to be challenging. However, for individual data (so this is another test that does not work for grouped data), the integral simplifies to
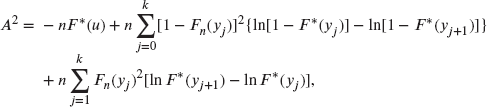
where the unique noncensored data points are 
. Note that when 
, the last term of the first sum is zero (evaluating the formula as written will ask for ln(0)). The critical values are 1.933, 2.492, and 3.857 for 10%, 5%, and 1% significance levels, respectively. As with the Kolmogorov–Smirnov test, the critical value should be smaller when 
.
15.4.3 The Chi-Square Goodness-of-Fit Test
Unlike the Kolmogorov–Smirnov and Anderson–Darling tests, this test allows for some discretion. It begins with the selection of 
arbitrary values, 
. Let 
be the probability a truncated observation falls in the interval from 
to 
. Similarly, let 
be the same probability according to the empirical distribution. The test statistic is then
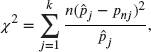
where n is the sample size. Another way to write the formula is to let 
be the number of expected observations in the interval (assuming that the hypothesized model is true) and let 
be the number of observations in the interval. Then,
The critical value for this test comes from the chi-square distribution with degrees of freedom equal to the number of terms in the sum (k) minus 1 minus the number of estimated parameters. There are a variety of rules that have been proposed for deciding when the test is reasonably accurate. They center around the values of 
. The most conservative states that each must be at least 5. Some authors claim that values as low as 1 are acceptable. All agree that the test works best when the values are about equal from term to term. If the data are grouped, there is little choice but to use the groups as given, although adjacent groups could be combined to increase 
. For individual data, the data can be grouped for the purpose of performing this test.7
Sometimes, the test can be modified to fit different situations. The following example illustrates this for aggregate frequency data.
There is one important point to note about these tests. Suppose that the sample size were to double but that the sampled values were not much different (imagine each number showing up twice instead of once). For the Kolmogorov–Smirnov test, the test statistic would be unchanged, but the critical value would be smaller. For the Anderson–Darling and chi-square tests, the test statistic would double while the critical value would be unchanged. As a result, for larger sample sizes, it is more likely that the null hypothesis (and, thus, the proposed model) would be rejected. This outcome should not be surprising. We know that the null hypothesis is false (it is extremely unlikely that a simple distribution using a few parameters can explain the complex behavior that produced the observations), and with a large enough sample size we will have convincing evidence of that truth. When using these tests, we must remember that although all our models are wrong, some may be useful.
15.4.4 The Likelihood Ratio Test
An alternative question to “Could the population have distribution A?” is “Is distribution B a more appropriate representation of the population than distribution A?” More formally:
To perform a formal hypothesis test, distribution A must be a special case of distribution B, for example, exponential versus gamma. An easy way to complete this test is given as follows.
This test makes some sense. When the alternative hypothesis is true, forcing the parameter to be selected from the null hypothesis should produce a likelihood value that is significantly smaller.
Table 15.11 Six useful models for Example 15.10.
| Model | Number of parameters | Negative loglikelihood |  |
p-value |
| Negative binomial | 2 | 5,348.04 | 8.77 | 0.0125 |
| ZM logarithmic | 2 | 5,343.79 | 4.92 | 0.1779 |
| Poisson–inverse Gaussian | 2 | 5,343.51 | 4.54 | 0.2091 |
| ZM negative binomial | 3 | 5,343.62 | 4.65 | 0.0979 |
| Geometric–negative binomial | 3 | 5,342.70 | 1.96 | 0.3754 |
| Poisson–ETNB | 3 | 5,342.51 | 2.75 | 0.2525 |
It is tempting to use this test when the alternative distribution simply has more parameters than the null distribution. In such cases, the test may not be appropriate. For example, it is possible for a two-parameter lognormal model to have a higher loglikelihood value than a three-parameter Burr model, resulting in a negative test statistic, indicating that a chi-square distribution is not appropriate. When the null distribution is a limiting (rather than special) case of the alternative distribution, the test may still be used, but the test statistic's distribution is now a mixture of chi-square distributions (see Self and Liang [112]). Regardless, it is still reasonable to use the “test” to make decisions in these cases, provided that it is clearly understood that a formal hypothesis test was not conducted.
15.4.5 Exercises
- 15.4 Use the Kolmogorov–Smirnov test to determine if a Weibull model is appropriate for the data used in Example 15.5.
- 15.5 (*) Five observations are made from a random variable. They are 1, 2, 3, 5, and 13. Determine the value of the Kolmogorov–Smirnov test statistic for the null hypothesis that
, 
. - 15.6 (*) You are given the following five observations from a random sample: 0.1, 0.2, 0.5, 1.0, and 1.3. Calculate the Kolmogorov–Smirnov test statistic for the null hypothesis that the population density function is
, 
. - 15.7 Perform the Anderson–Darling test of the Weibull distribution for Example 15.6.
- 15.8 Repeat Example 15.7 for the Weibull model.
- 15.9 (*) One hundred and fifty policyholders were observed from the time they arranged a viatical settlement until their death. No observations were censored. There were 21 deaths in the first year, 27 deaths in the second year, 39 deaths in the third year, and 63 deaths in the fourth year. The survival model
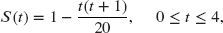
is being considered. At a 5% significance level, conduct the chi-square goodness-of-fit test.
- 15.10 (*) Each day, for 365 days, the number of claims is recorded. The results were 50 days with no claims, 122 days with one claim, 101 days with two claims, 92 days with three claims, and no days with four or more claims. For a Poisson model, determine the maximum likelihood estimate of
and then perform the chi-square goodness-of-fit test at a 2.5% significance level. - 15.11 (*) During a one-year period, the number of accidents per day was distributed as given in Table 15.12. Test the hypothesis that the data are from a Poisson distribution with mean 0.6, using the maximum number of groups such that each group has at least five expected observations. Use a significance level of 5%.
Table 15.12 The data for Exercise 15.11.
Number of accidents Days 0 209 1 111 2 33 3 7 4 3 5 2 - 15.12 (*) One thousand values were simulated from a uniform (0,1) distribution. The results were grouped into 20 ranges of equal width. The observed counts in each range were squared and added, resulting in a sum of 51,850. Determine the p-value for the chi-square goodness-of-fit test.
- 15.13 (*) Twenty claim amounts were sampled from a Pareto distribution with
and 
unknown. The maximum likelihood estimate of 
is 7.0. Also, 
and 
. The likelihood ratio test is used to test the null hypothesis that 
. Determine the p-value for this test. - 15.14 Redo Example 15.8 assuming that each exposure unit has a geometric distribution. Conduct the approximate chi-square goodness-of-fit test. Is the geometric preferable to the Poisson model?
- 15.15 Using Data Set B (with the original largest value), determine if a gamma model is more appropriate than an exponential model. Recall that an exponential model is a gamma model with
. Useful values were obtained in Example 11.2. - 15.16 Use Data Set C to choose a model for the population that produced those numbers. Choose from the exponential, gamma, and transformed gamma models. Information for the first two distributions was obtained in Example 11.3 and Exercise 11.17, respectively.
- 15.17 Conduct the chi-square goodness-of-fit test for each of the models obtained in Exercise 12.3.
- 15.18 Conduct the chi-square goodness-of-fit test for each of the models obtained in Exercise 12.5.
- 15.19 Conduct the chi-square goodness-of-fit test for each of the models obtained in Exercise 12.6.
- 15.20 For the data in Table 15.20, determine the method of moments estimates of the parameters of the Poisson–Poisson distribution where the secondary distribution is the ordinary (not zero-truncated) Poisson distribution. Perform the chi-square goodness-of-fit test using this model.
- 15.21 You are given the data in Table 15.13, which represent results from 23,589 automobile insurance policies. The third column, headed “Fitted model,” represents the expected number of losses for a fitted (by maximum likelihood) negative binomial distribution.
- Perform the chi-square goodness-of-fit test at a significance level of 5%.
- Determine the maximum likelihood estimates of the negative binomial parameters r and
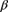. This can be done from the given numbers without actually maximizing the likelihood function.
Table 15.13 The data for Exercise 15.21.
Number of losses, k Number of policies, 
Fitted model 0 20,592 20,596.76 1 2,651 2,631.03 2 297 318.37 3 41 37.81 4 7 4.45 5 0 0.52 6 1 0.06 
0 0.00
15.5 Selecting a Model
15.5.1 Introduction
Almost all of the tools are now in place for choosing a model. Before outlining a recommended approach, two important concepts must be introduced. The first is parsimony. The principle of parsimony states that unless there is considerable evidence to do otherwise, a simpler model is preferred. The reason for this preference is that a complex model may do a great job of matching the data, but that is no guarantee that the model will match the population from which the observations were sampled. For example, given any set of 10 
pairs with unique x values, there will always be a polynomial of degree 9 or less that goes through all 10 points. But if these points were a random sample, it is highly unlikely that the population values would all lie on that polynomial. However, there may be a straight line that comes close to the sampled points as well as the other points in the population. This observation matches the spirit of most hypothesis tests. That is, do not reject the null hypothesis (and thus claim a more complex description of the population holds) unless there is strong evidence to do so.
The second concept does not have a name. It states that, if you try enough models, one will look good, even if it is not. Suppose that I have 900 models at my disposal. For most data sets, it is likely that one of them will fit extremely well, but it may not help us learn about the population.
Thus, in selecting models, there are two things to keep in mind:
- Use a simple model if at all possible.
- Restrict the universe of potential models.
The methods outlined in the remainder of this section help with the first point; the second one requires some experience. Certain models make more sense in certain situations, but only experience can enhance the modeler's senses so that only a short list of quality candidates is considered.
The section is split into two types of selection criteria. The first set is based on the modeler's judgment, while the second set is more formal in the sense that most of the time all analysts will reach the same conclusions because the decisions are made based on numerical measurements rather than charts or graphs.
15.5.2 Judgment-Based Approaches
Using judgment to select models involves one or more of the three concepts outlined herein. In all cases, the analyst's experience is critical.
First, the decision can be based on the various graphs (or tables based on the graphs) presented in this chapter, allowing the analyst to focus on aspects of the model that are important for the proposed application.9 For example, it may be more important to fit the tail well or it may be more important to match the mode or modes. Even if a score-based approach is used, it may be appropriate to present a convincing picture to support the chosen model.
Second, the decision can be influenced by the success of particular models in similar situations or the value of a particular model for its intended use. For example, the 1941 CSO mortality table follows a Makeham distribution for much of its range of ages. In a time of limited computing power, such a distribution allowed for easier calculation of joint life values. As long as the fit of this model was reasonable, this advantage outweighed the use of a different, but better fitting, model. Similarly, if the Pareto distribution has been used to model a particular line of liability insurance both by the analyst's company and by others, it may require more than the usual amount of evidence to change to an alternative distribution.
Third, the situation may completely determine the distribution. For example, suppose that a dental insurance contract provides for at most two checkups per year and suppose that individuals make two independent choices each year as to whether to have a checkup. If each time the probability is q, then the distribution must be binomial with 
.
Finally, it should be noted that the more algorithmic approaches outlined in this section do not always agree. In that case, judgment is most definitely required, if only to decide which algorithmic approach to use.
15.5.3 Score-Based Approaches
Some analysts might prefer an automated process for selecting a model. An easy way to do that would be to assign a score to each model and let the model with the best value win. The following scores are worth considering:
- The Kolmogorov–Smirnov test statistic: Choose the model with the smallest value.
- The Anderson–Darling test statistic: Choose the model with the smallest value.
- The chi-square goodness-of-fit test statistic: Choose the model with the smallest value.
- The chi-square goodness-of-fit test: Choose the model with the highest p-value.
- The likelihood (or loglikelihood) function at its maximum: Choose the model with the largest value.
All but the chi-square p-value have a deficiency with respect to parsimony. First, consider the likelihood function. When comparing, say, an exponential to a Weibull model, the Weibull model must have a likelihood value that is at least as large as that of the exponential model. They would only be equal in the rare case that the maximum likelihood estimate of the Weibull parameter 
was equal to 1. Thus, the Weibull model would always win over the exponential model, a clear violation of the principle of parsimony. For the three test statistics, there is no assurance that the same relationship will hold, but it seems likely that, if a more complex model is selected, the fit measure will be better. The only reason the chi-square test p-value is immune from this problem is that with more complex models, the test has fewer degrees of freedom. It is then possible that the more complex model will have a smaller p-value. There is no comparable adjustment for the first two test statistics listed.
With regard to the likelihood value, there are two ways to proceed. One is to perform the likelihood ratio test and the other is to impose a penalty for employing additional parameters. The likelihood ratio test is technically only available when one model is a special case of another (e.g. Pareto versus generalized Pareto). The concept can be turned into an algorithm by using the test at a 5% significance level. Begin with the best one-parameter model (the one with the highest loglikelihood value). Add a second parameter only if the two-parameter model with the highest loglikelihood value shows an increase of at least 1.92 (so that twice the difference exceeds the critical value of 3.84). Then move to three-parameter models. If the comparison is to a two-parameter model, a 1.92 increase is again needed. If the early comparison led to keeping the one-parameter model, an increase of 3.00 is needed (because the test has two degrees of freedom). To add three parameters requires a 3.91 increase; four parameters, a 4.74 increase; and so on. In the spirit of this chapter, this algorithm can be used even when one model is not a special case of the other model. However, it would not be appropriate to claim that a likelihood ratio test was being conducted.
Aside from the issue of special cases, the likelihood ratio test has the same problem as any hypothesis test. Were the sample size to double, the loglikelihoods would also double, making it more likely that a model with a higher number of parameters would be selected, tending to defeat the parsimony principle. Conversely, it could be argued that, if we possess a lot of data, we have the right to consider and fit more complex models. A method that effects a compromise between these positions is the Schwarz Bayesian Criterion (SBC) [110], which is also called the Bayesian Information Criterion (BIC). This method recommends that, when ranking models, a deduction of 
should be made from the loglikelihood value, where r is the number of estimated parameters and n is the sample size. Thus, adding a parameter requires an increase of 
in the loglikelihood. For larger sample sizes, a greater increase is needed, but it is not proportional to the sample size itself.
An alternative penalty is the Akaike Information Criterion (AIC) [4]. This method deducts the number of parameters from the loglikelihood.10 Section 3 of Brockett [17] promotes the AIC, while in a discussion of that paper Carlin provides support for the SBC. The difference in the two methods is that the SBC adjusts for the sample size while the AIC does not. To summarize, the scores are as follows:
Table 15.18 The test results for Example 15.14.
| Poisson | Geometric | ZM Poisson | ZM geometric | |
| Chi-square | 543.0 | 643.4 | 64.8 | 0.58 |
| Degrees of freedom | 2 | 4 | 2 | 2 |
| p-value |  |
 |
 |
 |
| Loglikelihood | −171,373 | −171,479 | −171,160 | −171,133 |
| SBC | −171,379.5 | −171,485.5 | −171,173 | −171,146 |
| AIC | −171,374 | −171,480 | −171,162 | −171,135 |
Table 15.19 The fit of the Simon data for Example 15.15.
| Fitted distributions | ||||
| Number of claims/contract | Number of contracts | Poisson | Negative binomial | Polya–Aeppli |
| 0 | 99 | 54.0 | 95.9 | 98.7 |
| 1 | 65 | 92.2 | 75.8 | 70.6 |
| 2 | 57 | 78.8 | 50.4 | 50.2 |
| 3 | 35 | 44.9 | 31.3 | 32.6 |
| 4 | 20 | 19.2 | 18.8 | 20.0 |
| 5 | 10 | 6.5 | 11.0 | 11.7 |
| 6 | 4 | 1.9 | 6.4 | 6.6 |
| 7 | 0 | 0.5 | 3.7 | 3.6 |
| 8 | 3 | 0.1 | 2.1 | 2.0 |
| 9 | 4 | 0.0 | 1.2 | 1.0 |
| 10 | 0 | 0.0 | 0.7 | 0.5 |
| 11 | 1 | 0.0 | 0.4 | 0.3 |
| 12+ | 0 | 0.0 | 0.5 | 0.3 |
| Parameters |  |
 |
 |
|
 |
 |
|||
| Chi-square | 72.64 | 4.06 | 2.84 | |
| Degrees of freedom | 4 | 5 | 5 | |
| p-Value |  |
54.05% | 72.39% | |
| Loglikelihood | −577.0 | −528.8 | −528.5 | |
| SBC | −579.8 | −534.5 | −534.2 | |
| AIC | −578.0 | −530.8 | −530.5 | |
15.5.4 Exercises
- 15.22 (*) One thousand policies were sampled and the number of accidents for each recorded. The results are shown in Table 15.23. Without doing any formal tests, determine which of the following five models is most appropriate: binomial, Poisson, negative binomial, normal, or gamma.
Table 15.23 The data for exercise 15.22.
Number of accidents Number of policies 0 100 1 267 2 311 3 208 4 87 5 23 6 4 Total 1,000 - 15.23 For Example 15.1, determine if a transformed gamma model is more appropriate than either the exponential model or the Weibull model for each of the three data sets.
- 15.24 (*) From the data in Exercise 15.11, the maximum likelihood estimates are
for the Poisson distribution and 
and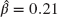 
for the negative binomial distribution. Conduct the likelihood ratio test for choosing between these two models. - 15.25 (*) From a sample of size 100, five models are fitted with the results given in Table 15.24. Use the SBC and then the AIC to select the best model.
Table 15.24 The results for exercise 15.25.
Model Number of parameters Negative loglikelihood Generalized Pareto 3 219.1 Burr 3 219.2 Pareto 2 221.2 Lognormal 2 221.4 Inverse exponential 1 224.3 - 15.26 Refer to Exercise 11.27. Use the likelihood ratio test (at a 5% significance level), the SBC, and the AIC to decide if Sylvia's claim is true.
- 15.27 (*) Five models were fitted to a sample of 260 observations. The following are the number of parameters in the model followed by the loglikelihood value: 1, −414, 2, −412, 3, −411, 4, −409, 6, −409. According to the SBC, which model (identified by the number of parameters) should be selected? Does the decision change if the AIC is used?
- 15.28 Using results from Exercises 12.3 and 15.17, use the chi-square goodness-of-fit test, the likelihood ratio test, the SBC, and the AIC to determine the best model from the members of the
class. - 15.29 Using results from Exercises 12.5 and 15.18, use the chi-square goodness-of-fit test, the likelihood ratio test, the SBC, and the AIC to determine the best model from the members of the
class. - 15.30 Using results from Exercises 12.6 and 15.19, use the chi-square goodness-of-fit test, the likelihood ratio test, the SBC, and the AIC to determine the best model from the members of the
class. - 15.31 Table 15.25 gives the number of medical claims per reported automobile accident.
Table 15.25 The data for exercise 15.31.
Number of medical claims Number of accidents 0 529 1 146 2 169 3 137 4 99 5 87 6 41 7 25 8+ 0 - Construct a plot similar to Figure 6.1. Does it appear that a member of the
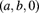class will provide a good model? If so, which one? - Determine the maximum likelihood estimates of the parameters for each member of the
class. - Based on the chi-square goodness-of-fit test, the likelihood ratio test, the SBC, and the AIC, which member of the
class provides the best fit? Is this model acceptable?
- Construct a plot similar to Figure 6.1. Does it appear that a member of the
- 15.32 For the four data sets introduced in Exercises 12.3, 12.5, 12.6, and 15.31, you have determined the best model from among members of the
class. For each data set, determine the maximum likelihood estimates of the zero-modified Poisson, geometric, logarithmic, and negative binomial distributions. Use the chi-square goodness-of-fit test and likelihood ratio tests to determine the best of the eight models considered and state whether the selected model is acceptable. - 15.33 A frequency model that has not been mentioned to this point is the zeta distribution. It is a zero-truncated distribution with
, 
. The denominator is the zeta function, which must be evaluated numerically as 
. The zero-modified zeta distribution can be formed in the usual way. More information can be found in Luong and Doray [84].
- Determine the maximum likelihood estimates of the parameters of the zero-modified zeta distribution for the data in Example 12.7.
- Is the zero-modified zeta distribution acceptable?
- 15.34 In Exercise 15.32, the best model from among the members of the
and 
classes was selected for the data sets in Exercises 12.3, 12.5, 12.6, and 15.31. Fit the Poisson–Poisson, Polya–Aeppli, Poisson–inverse Gaussian, and Poisson–ETNB distributions to these data and determine if any of these distributions should replace the one selected in Exercise 15.32. Is the current best model acceptable? - 15.35 The five data sets presented in this problem are all taken from Lemaire [79]. For each data set, compute the first three moments and then use the ideas in Section 7.2 to make a guess at an appropriate model from among the compound Poisson collection [(Poisson, geometric, negative binomial, Poisson–binomial (with
and 
), Polya–Aeppli, Neyman Type A, Poisson–inverse Gaussian, and Poisson–ETNB)]. From the selected model (if any) and members of the 
and 
classes, determine the best model.
- The data in Table 15.26 represent counts from third-party automobile liability coverage in Belgium.
Table 15.26 The data for exercise 15.35(a).
Number of claims Number of policies 0 96,978 1 9,240 2 704 3 43 4 9 5+ 0 - The data in Table 15.27 represent the number of deaths due to horse kicks in the Prussian army between 1875 and 1894. The counts are the number of deaths in a corps (there were 10 of them) in a given year, and thus there are 200 observations. This data set is often cited as the inspiration for the Poisson distribution. For using any of our models, what additional assumption about the data must be made?
Table 15.27 The data for exercise 15.35(b).
Number of deaths Number of corps 0 109 1 65 2 22 3 3 4 1 5+ 0 - The data in Table 15.28 represent the number of major international wars per year from 1500 through 1931.
Table 15.28 The data for exercise 15.35(c).
Number of wars Number of years 0 223 1 142 2 48 3 15 4 4 5+ 0 - The data in Table 15.29 represent the number of runs scored in each half-inning of World Series baseball games played from 1947 through 1960.
Table 15.29 The data for exercise 15.35(d).
Number of runs Number of half innings 0 1,023 1 222 2 87 3 32 4 18 5 11 6 6 7+ 3 - The data in Table 15.30 represent the number of goals per game per team in the 1966–1967 season of the National Hockey League.
Table 15.30 The data for exercise 15.35(e).
Number of goals Number of games 0 29 1 71 2 82 3 89 4 65 5 45 6 24 7 7 8 4 9 1 10+ 3
- The data in Table 15.26 represent counts from third-party automobile liability coverage in Belgium.
- 15.36 Verify that the estimates presented in Example 7.14 are the maximum likelihood estimates. (Because only two decimals are presented, it is probably sufficient to observe that the likelihood function takes on smaller values at each of the nearby points.) The negative binomial distribution was fitted to these data in Example 12.5. Which of these two models is preferable?