6
Discrete Distributions
6.1 Introduction
The purpose of this chapter is to introduce a large class of counting distributions. Counting distributions are discrete distributions with probabilities only on the nonnegative integers, that is, probabilities are defined only at the points ![]() . In an insurance context, counting distributions can be used to describe the number of events such as losses to the insured or claims to the insurance company. An understanding of both the number of claims and the size of claims provides a deeper insight into a variety of issues surrounding insurance payments than if information is only available about total losses. The description of total losses in terms of numbers and amounts separately makes it possible to address issues of modification of an insurance contract. Another reason for separating numbers and amounts of claims is that models for the number of claims are fairly easy to obtain, and experience has shown that the commonly used distributions really do model the propensity to generate losses.
. In an insurance context, counting distributions can be used to describe the number of events such as losses to the insured or claims to the insurance company. An understanding of both the number of claims and the size of claims provides a deeper insight into a variety of issues surrounding insurance payments than if information is only available about total losses. The description of total losses in terms of numbers and amounts separately makes it possible to address issues of modification of an insurance contract. Another reason for separating numbers and amounts of claims is that models for the number of claims are fairly easy to obtain, and experience has shown that the commonly used distributions really do model the propensity to generate losses.
We now formalize some of the notation used for models for discrete phenomena. The probability function (pf) ![]() denotes the probability that exactly k events (such as claims or losses) occur. Let N be a random variable representing the number of such events. Then,
denotes the probability that exactly k events (such as claims or losses) occur. Let N be a random variable representing the number of such events. Then,
As a reminder, the probability generating function (pgf) of a discrete random variable N with pf ![]() is
is
As is true with the moment generating function, the pgf can be used to generate moments. In particular, ![]() and
and ![]() (see Exercise 6.1). To see that the pgf really does generate probabilities, observe that
(see Exercise 6.1). To see that the pgf really does generate probabilities, observe that

6.1.1 Exercise
- 6.1 The moment generating function (mgf) for discrete variables is defined as

Demonstrate that
 . Use the fact that
. Use the fact that  to show that
to show that  and
and  .
.
6.2 The Poisson Distribution
The pf for the Poisson distribution is
The probability generating function from Example 3.8 is
The mean and variance can be computed from the probability generating function as follows:

For the Poisson distribution, the variance is equal to the mean. The Poisson distribution and Poisson processes (which give rise to Poisson distributions) are discussed in many textbooks on probability, statistics, and actuarial science, including Panjer and Willmot [100] and Ross [109].
The Poisson distribution has at least two additional useful properties. The first is given in the following theorem.
![]()
The second property is particularly useful in modeling insurance risks. Suppose that the number of claims in a fixed time period, such as one year, follows a Poisson distribution. Further suppose that the claims can be classified into m distinct types. For example, claims could be classified by size, such as those below a fixed limit and those above the limit. It turns out that, if we are interested in studying the number of claims above the limit, that distribution is also Poisson but with a new Poisson parameter.
This second property is also useful when considering removing or adding a part of an insurance coverage. Suppose that the number of claims for a complicated medical benefit coverage follows a Poisson distribution. Consider the “types” of claims to be the different medical procedures or medical benefits under the plan. If one of the benefits is removed from the plan, again it turns out that the distribution of the number of claims under the revised plan will still have a Poisson distribution, but with a new parameter.
In each of the cases mentioned in the previous paragraph, the number of claims of the different types will not only be Poisson distributed but will also be independent of each other, that is, the distributions of the number of claims above the limit and the number below the limit will be independent of each other. This is a somewhat surprising result. For example, suppose that we, the insurer, currently sell an insurance policy with a deductible of 50 and experience has indicated that a Poisson distribution with a certain parameter is a valid model for the number of payments. Further suppose that we are also comfortable with the assumption that the number of losses in a period also has the Poisson distribution but we do not know the parameter. Without additional information, it is impossible to infer the value of the Poisson parameter should the deductible be lowered or removed entirely. We now formalize these ideas in the following theorem.
![]()
![]()
6.3 The Negative Binomial Distribution
The negative binomial distribution has been used extensively as an alternative to the Poisson distribution. Like the Poisson distribution, it has positive probabilities on the nonnegative integers. Because it has two parameters, it has more flexibility in shape than the Poisson.
It is not difficult to show that the probability generating function for the negative binomial distribution is
From this, it follows that the mean and variance of the negative binomial distribution are
Because ![]() is positive, the variance of the negative binomial distribution exceeds the mean. This relationship is in contrast to the Poisson distribution, for which the variance is equal to the mean. Thus, for a particular set of data, if the observed variance is larger than the observed mean, the negative binomial might be a better candidate than the Poisson distribution as a model to be used.
is positive, the variance of the negative binomial distribution exceeds the mean. This relationship is in contrast to the Poisson distribution, for which the variance is equal to the mean. Thus, for a particular set of data, if the observed variance is larger than the observed mean, the negative binomial might be a better candidate than the Poisson distribution as a model to be used.
The negative binomial distribution is a generalization of the Poisson in at least two different ways, namely, as a mixed Poisson distribution with a gamma mixing distribution (demonstrated later in this section) and as a compound Poisson distribution with a logarithmic secondary distribution (see Section 7.1).
The geometric distribution is the special case of the negative binomial distribution when ![]() . The geometric distribution is, in some senses, the discrete analog of the continuous exponential distribution. Both the geometric and exponential distributions have an exponentially decaying probability function and, hence, the memoryless property, which can be interpreted in various contexts as follows. If the exponential distribution is a distribution of lifetimes, then the expected future lifetime is constant for any age. If the exponential distribution describes the size of insurance claims, then the memoryless property can be interpreted as follows: Given that a claim exceeds a certain level d, the expected amount of the claim in excess of d is constant and so does not depend on d. That is, if a deductible of d is imposed, the expected payment per claim will be unchanged but, of course, the expected number of payments will decrease. If the geometric distribution describes the number of claims, then the memoryless property can be interpreted as follows: Given that there are at least m claims, the probability distribution of the number of claims in excess of m does not depend on m. Among continuous distributions, the exponential distribution is used to distinguish between subexponential distributions with heavy (or fat) tails and distributions with light (or thin) tails. Similarly for frequency distributions, distributions that decay in the tail slower than the geometric distribution are often considered to have heavy tails, whereas distributions that decay more rapidly than the geometric have light tails. The negative binomial distribution has a heavy tail (decays more slowly than the geometric distribution) when
. The geometric distribution is, in some senses, the discrete analog of the continuous exponential distribution. Both the geometric and exponential distributions have an exponentially decaying probability function and, hence, the memoryless property, which can be interpreted in various contexts as follows. If the exponential distribution is a distribution of lifetimes, then the expected future lifetime is constant for any age. If the exponential distribution describes the size of insurance claims, then the memoryless property can be interpreted as follows: Given that a claim exceeds a certain level d, the expected amount of the claim in excess of d is constant and so does not depend on d. That is, if a deductible of d is imposed, the expected payment per claim will be unchanged but, of course, the expected number of payments will decrease. If the geometric distribution describes the number of claims, then the memoryless property can be interpreted as follows: Given that there are at least m claims, the probability distribution of the number of claims in excess of m does not depend on m. Among continuous distributions, the exponential distribution is used to distinguish between subexponential distributions with heavy (or fat) tails and distributions with light (or thin) tails. Similarly for frequency distributions, distributions that decay in the tail slower than the geometric distribution are often considered to have heavy tails, whereas distributions that decay more rapidly than the geometric have light tails. The negative binomial distribution has a heavy tail (decays more slowly than the geometric distribution) when ![]() and a lighter tail than the geometric distribution when
and a lighter tail than the geometric distribution when ![]() .
.
As noted earlier, one way to create the negative binomial distribution is as a mixture of Poissons. Suppose that we know that a risk has a Poisson number of claims distribution when the risk parameter ![]() is known. Now treat
is known. Now treat ![]() as being the outcome of a random variable
as being the outcome of a random variable ![]() . We denote the pdf/pf of
. We denote the pdf/pf of ![]() by
by ![]() , where
, where ![]() may be continuous or discrete, and denote the cdf by
may be continuous or discrete, and denote the cdf by ![]() . The idea that
. The idea that ![]() is the outcome of a random variable can be justified in several ways. First, we can think of the population of risks as being heterogeneous with respect to the risk parameter
is the outcome of a random variable can be justified in several ways. First, we can think of the population of risks as being heterogeneous with respect to the risk parameter ![]() . In practice, this makes sense. Consider a portfolio of insurance policies with the same premium, such as a group of automobile drivers in the same rating category. Such categories are usually broad ranges, such as 0–7,500 miles driven per year, garaged in a rural area, commuting less than 50 miles per week, and so on. We know that not all drivers in the same rating category are the same, even though they may “appear” to be the same from the point of view of the insurer and are charged the same premium. The parameter
. In practice, this makes sense. Consider a portfolio of insurance policies with the same premium, such as a group of automobile drivers in the same rating category. Such categories are usually broad ranges, such as 0–7,500 miles driven per year, garaged in a rural area, commuting less than 50 miles per week, and so on. We know that not all drivers in the same rating category are the same, even though they may “appear” to be the same from the point of view of the insurer and are charged the same premium. The parameter ![]() measures the expected number of accidents for a given driver. If
measures the expected number of accidents for a given driver. If ![]() varies across the population of drivers, then we can think of the insured individual as a sample value drawn from the population of possible drivers. For a particular driver,
varies across the population of drivers, then we can think of the insured individual as a sample value drawn from the population of possible drivers. For a particular driver, ![]() is unknown to the insurer but follows some distribution, in this case
is unknown to the insurer but follows some distribution, in this case ![]() , over the population of drivers. The true value of
, over the population of drivers. The true value of ![]() is unobservable. We can only observe the number of accidents coming from the driver. There is now an additional degree of uncertainty, that is, uncertainty about the parameter.
is unobservable. We can only observe the number of accidents coming from the driver. There is now an additional degree of uncertainty, that is, uncertainty about the parameter.
This is the same mixing process that was discussed with regard to continuous distributions in Section 5.2.4. In some contexts, this is referred to as parameter uncertainty. In the Bayesian context, the distribution of ![]() is called a prior distribution and the parameters of its distribution are sometimes called hyperparameters. The role of the distribution
is called a prior distribution and the parameters of its distribution are sometimes called hyperparameters. The role of the distribution ![]() is very important in credibility theory, the subject of Chapter 16. When the parameter
is very important in credibility theory, the subject of Chapter 16. When the parameter ![]() is unknown, the probability that exactly k claims will arise can be written as the expected value of the same probability but conditional on
is unknown, the probability that exactly k claims will arise can be written as the expected value of the same probability but conditional on ![]() , where the expectation is taken with respect to the distribution of
, where the expectation is taken with respect to the distribution of ![]() . From the law of total probability, we can write
. From the law of total probability, we can write

Now suppose that ![]() has a gamma distribution. Then,
has a gamma distribution. Then,
From the definition of the gamma distribution in Appendix A, this expression can be evaluated as

This formula is of the same form as (6.2), demonstrating that the mixed Poisson, with a gamma mixing distribution, is the same as a negative binomial distribution.
It is worth noting that the Poisson distribution is a limiting case of the negative binomial distribution. To see this, let r go to infinity and ![]() go to zero while keeping their product constant. Let
go to zero while keeping their product constant. Let ![]() be that constant. Substitution of
be that constant. Substitution of ![]() in the pgf leads to (using L'Hôpital's rule in lines 3 and 5)
in the pgf leads to (using L'Hôpital's rule in lines 3 and 5)

which is the pgf of the Poisson distribution.
6.4 The Binomial Distribution
The binomial distribution is another counting distribution that arises naturally in claim number modeling. It possesses some properties different from those of the Poisson and the negative binomial that make it particularly useful. First, its variance is smaller than its mean, making it useful for data sets in which the observed sample variance is less than the sample mean. This property contrasts with the negative binomial, where the variance exceeds the mean, and it also contrasts with the Poisson distribution, where the variance is equal to the mean.
Second, it describes a physical situation in which m risks are each subject to claim or loss. We can formalize this situation as follows. Consider m independent and identical risks, each with probability q of making a claim.1 This might apply to a life insurance situation in which all the individuals under consideration are in the same mortality class, that is, they may all be male smokers at age 35 and duration 5 of an insurance policy. In that case, q is the probability that a person with those attributes will die in the next year. Then, the number of claims for a single person follows a Bernoulli distribution, a distribution with probability ![]() at 0 and probability q at 1. The probability generating function of the number of claims per individual is then given by
at 0 and probability q at 1. The probability generating function of the number of claims per individual is then given by
Now, if there are m such independent individuals, then the probability generating functions can be multiplied together to give the probability generating function of the total number of claims arising from the group of m individuals. That probability generating function is
Then, from this it is easy to show that the probability of exactly k claims from the group is
the pf for a binomial distribution with parameters m and q. From this Bernoulli trial framework, it is clear that at most m events (claims) can occur. Hence, the distribution only has positive probabilities on the nonnegative integers up to and including m.
Consequently, a sometimes useful attribute of the binomial distribution is that it has finite support, that is, the range of values for which there exist positive probabilities has finite length. This attribute may be useful, for instance, in modeling the number of individuals injured in an automobile accident or the number of family members covered under a health insurance policy. In each case, it is reasonable to have an upper limit on the range of possible values. It is useful also in connection with situations in which it is believed that it is unreasonable to assign positive probabilities beyond some point. For example, if we are modeling the number of accidents per automobile during a one-year period, it is probably physically impossible for there to be more than some number, say 12, of claims during the year, given the time it would take to repair the automobile between accidents. If a model with probabilities that extend beyond 12 were used, those probabilities should be very small, so that they have little impact on any decisions that are made.
The mean and variance of the binomial distribution are given by
6.5 The (a,b,0) Class
The following definition characterizes the members of this class of distributions.
This recursion describes the relative size of successive probabilities in the counting distribution. The probability at zero, ![]() , can be obtained from the recursive formula because the probabilities must sum to 1. The
, can be obtained from the recursive formula because the probabilities must sum to 1. The ![]() class of distributions is a two-parameter class, the two parameters being a and b. The following example illustrates these ideas by demonstrating that the binomial distribution is a member of the
class of distributions is a two-parameter class, the two parameters being a and b. The following example illustrates these ideas by demonstrating that the binomial distribution is a member of the ![]() class.
class.
![]()
As in the above example, substituting in the probability function for the Poisson and negative binomial distributions on each side of the recursive formula in Definition 6.4, with the values of a and b given in Table 6.1, demonstrates that these two distributions are also members of the ![]() class. In addition, Table 6.1 gives the values of
class. In addition, Table 6.1 gives the values of ![]() , the starting value for the recursion. The geometric distribution, the one-parameter special case
, the starting value for the recursion. The geometric distribution, the one-parameter special case ![]() of the negative binomial distribution, is also in the table.
of the negative binomial distribution, is also in the table.
Table 6.1 The members of the ![]() class.
class.
| Distribution | a | b | |
| Poisson | 0 | ||
| Binomial | |||
| Negative binomial | |||
| Geometric | 0 |
It can be shown (see Panjer and Willmot [100, Chapter 6]) that these are the only possible distributions satisfying this recursive formula.
The recursive formula can be rewritten (if ![]() ) as
) as
The expression on the left-hand side is a linear function in k. Note from Table 6.1 that the slope a of the straight line is zero for the Poisson distribution, is negative for the binomial distribution, and is positive for the negative binomial distribution, including the geometric special case. This relationship suggests a graphical way of indicating which of the three distributions might be selected for fitting to data. We begin by plotting
against k. The observed values should form approximately a straight line if one of these models is to be selected, and the value of the slope should be an indication of which of the models should be selected. Note that this cannot be done if any of the ![]() are zero. Hence this procedure is less useful for a small number of observations.
are zero. Hence this procedure is less useful for a small number of observations.
![]()
Table 6.2 The accident profile from Thyrion [120].
| Number of accidents, k | Number of policies, |
|
| 0 | 7,840 | |
| 1 | 1,317 | 0.17 |
| 2 | 239 | 0.36 |
| 3 | 42 | 0.53 |
| 4 | 14 | 1.33 |
| 5 | 4 | 1.43 |
| 6 | 4 | 6.00 |
| 7 | 1 | 1.75 |
| 8+ | 0 | |
| Total | 9,461 |

Figure 6.1 The plot of the ratio  against k.
against k.
It is also possible to compare the appropriateness of the distributions by looking at the relationship of the variance to the mean. For this data set, the mean number of claims per policy is 0.2144. The variance is 0.2889. Because the variance exceeds the mean, the negative binomial should be considered as an alternative to the Poisson. Again, this is a qualitative comment because we have, at this point, no formal way of determining whether the variance is sufficiently larger than the mean to warrant use of the negative binomial. To do some formal analysis, Table 6.3 gives the results of maximum likelihood estimation (discussed in Chapters 11 and 12) of the parameters of the Poisson and negative binomial distributions and the negative loglikelihood in each case. In Chapter 15, formal selection methods are presented. They would indicate that the negative binomial is superior to the Poisson as a model for this data set. However, those methods also indicate that the negative binomial is not a particularly good model and, thus, some of the distributions yet to be introduced should be considered.
Table 6.3 Comparison between Poisson and negative binomial models.
| Distribution | Parameter estimates | |
| Poisson | 5,490.78 | |
| Negative binomial | 5,348.04 | |
In subsequent sections, we will expand the class of the distributions beyond the three discussed in this section by constructing more general models related to the Poisson, binomial, and negative binomial distributions.
6.5.1 Exercises
- 6.2 For each of the data sets in Exercises 12.3 and 12.5 in Section 12.7, calculate values similar to those in Table 6.2. For each, determine the most appropriate model from the
 class.
class. - 6.3 Use your knowledge of the permissible ranges for the parameters of the Poisson, negative binomial, and binomial to determine all possible values of a and b for these members of the
 class. Because these are the only members of the class, all other pairs must not lead to a legitimate probability distribution (nonnegative values that sum to 1). Show that the pair
class. Because these are the only members of the class, all other pairs must not lead to a legitimate probability distribution (nonnegative values that sum to 1). Show that the pair  and
and  (which is not on the list of possible values) does not lead to a legitimate distribution.
(which is not on the list of possible values) does not lead to a legitimate distribution.
6.6 Truncation and Modification at Zero
At times, the distributions discussed previously do not adequately describe the characteristics of some data sets encountered in practice. This may be because the tail of the negative binomial is not heavy enough or because the distributions in the ![]() class cannot capture the shape of the data set in some other part of the distribution.
class cannot capture the shape of the data set in some other part of the distribution.
In this section, we address the problem of a poor fit at the left-hand end of the distribution, in particular, the probability at zero.
For insurance count data, the probability at zero is the probability that no claims occur during the period under study. For applications in insurance where the probability of occurrence of a loss is very small, the probability at zero has the largest value. Thus, it is important to pay special attention to the fit at this point.
There are also situations that naturally occur which generate unusually large probabilities at zero. Consider the case of group dental insurance. If, in a family, both husband and wife have coverage with their respective employer-sponsored plans and both group insurance contracts provide coverage for all family members, the claims will be made to the insurer of the plan that provides the better benefits, and no claims may be made under the other contract. Then, in conducting studies for a specific insurer, we may find a higher than expected number of individuals who made no claim.
Similarly, it is possible to have situations in which there is less than the expected number, or even zero, occurrences at zero. For example, if we are counting the number of claims from accidents resulting in a claim, the minimum observed value is 1.
An adjustment of the probability at zero is easily handled for the Poisson, binomial, and negative binomial distributions.
Note that the only difference from the ![]() class is that the recursion begins at
class is that the recursion begins at ![]() rather than
rather than ![]() . The distribution from
. The distribution from ![]() to
to ![]() has the same shape as the
has the same shape as the ![]() class in the sense that the probabilities are the same up to a constant of proportionality, because
class in the sense that the probabilities are the same up to a constant of proportionality, because ![]() can be set to any number in the interval
can be set to any number in the interval ![]() . The remaining probability is at
. The remaining probability is at ![]() .
.
We distinguish between the situations in which ![]() and those where
and those where ![]() . The first subclass is called the truncated (more specifically, zero-truncated) distributions. The members are the zero-truncated Poisson, zero-truncated binomial, and zero-truncated negative binomial distributions (and the special case of the latter, the zero-truncated geometric distribution).
. The first subclass is called the truncated (more specifically, zero-truncated) distributions. The members are the zero-truncated Poisson, zero-truncated binomial, and zero-truncated negative binomial distributions (and the special case of the latter, the zero-truncated geometric distribution).
The second subclass is referred to as the zero-modified distributions because the probability is modified from that for the ![]() class. These distributions can be viewed as a mixture of an
class. These distributions can be viewed as a mixture of an ![]() distribution and a degenerate distribution with all the probability at zero. Alternatively, they can be called truncated with zeros distributions because the distribution can be viewed as a mixture of a truncated distribution and a degenerate distribution with all the probability at zero. We now show this equivalence more formally. Note that all zero-truncated distributions can be considered as zero-modified distributions, with the particular modification being to set
distribution and a degenerate distribution with all the probability at zero. Alternatively, they can be called truncated with zeros distributions because the distribution can be viewed as a mixture of a truncated distribution and a degenerate distribution with all the probability at zero. We now show this equivalence more formally. Note that all zero-truncated distributions can be considered as zero-modified distributions, with the particular modification being to set ![]() . The abbreviations ZT and ZM will be used at times. For example, a reference to the ZT Poisson distribution.
. The abbreviations ZT and ZM will be used at times. For example, a reference to the ZT Poisson distribution.
With three types of distributions, the notation can become confusing. When writing about discrete distributions in general, we continue to let ![]() . When referring to a zero-truncated distribution, we use
. When referring to a zero-truncated distribution, we use ![]() , and when referring to a zero-modified distribution, we use
, and when referring to a zero-modified distribution, we use ![]() . Once again, it is possible for a zero-modified distribution to be a zero-truncated distribution.
. Once again, it is possible for a zero-modified distribution to be a zero-truncated distribution.
Let ![]() denote the pgf of a member of the
denote the pgf of a member of the ![]() class. Let
class. Let ![]() denote the pgf of the corresponding member of the
denote the pgf of the corresponding member of the ![]() class, that is,
class, that is,
and ![]() is an arbitrary number. Then,
is an arbitrary number. Then,

Because ![]() ,
,
resulting in
This relationship is necessary to ensure that the ![]() sum to 1. We then have
sum to 1. We then have
This is a weighted average of the pgfs of the degenerate distribution and the corresponding ![]() member. Furthermore,
member. Furthermore,
Let ![]() denote the pgf of the zero-truncated distribution corresponding to an
denote the pgf of the zero-truncated distribution corresponding to an ![]() pgf
pgf ![]() . Then, by setting
. Then, by setting ![]() in (6.4) and (6.5),
in (6.4) and (6.5),
and
Then, from (6.5),
and
Then, the zero-modified distribution is also the weighted average of a degenerate distribution and the zero-truncated member of the ![]() class. The following example illustrates these relationships.
class. The following example illustrates these relationships.
![]()
A special case of the zero-modified distributions is called zero-inflated. The only difference is that for such distributions it is required that ![]() . It is shown in Frees [41] that for the zero-inflated Poisson distribution the variance is always larger than the mean. This provides an alternative to the negative binomial model when that property is desired.
. It is shown in Frees [41] that for the zero-inflated Poisson distribution the variance is always larger than the mean. This provides an alternative to the negative binomial model when that property is desired.
Although we have only discussed the zero-modified distributions of the ![]() class, the
class, the ![]() class admits additional distributions. The
class admits additional distributions. The ![]() parameter space can be expanded to admit an extension of the negative binomial distribution to include cases where
parameter space can be expanded to admit an extension of the negative binomial distribution to include cases where ![]() . For the
. For the ![]() class,
class, ![]() is required. By adding the additional region to the sample space, the “extended” truncated negative binomial (ETNB) distribution has parameter restrictions
is required. By adding the additional region to the sample space, the “extended” truncated negative binomial (ETNB) distribution has parameter restrictions ![]() ,
, ![]() ,
, ![]() .
.
To show that the recursive equation
with ![]() defines a proper distribution, it is sufficient to show that for any value of
defines a proper distribution, it is sufficient to show that for any value of ![]() , the successive values of
, the successive values of ![]() obtained recursively are each positive and that
obtained recursively are each positive and that ![]() . For the ETNB, this must be done for the parameter space
. For the ETNB, this must be done for the parameter space
(see Exercise 6.4).
When ![]() , the limiting case of the ETNB is the logarithmic distribution with
, the limiting case of the ETNB is the logarithmic distribution with
(see Exercise 6.5). The pgf of the logarithmic distribution is
(see Exercise 6.6). The zero-modified logarithmic distribution is created by assigning an arbitrary probability at zero and reducing the remaining probabilities.
It is also interesting that the special extreme case with ![]() and
and ![]() is a proper distribution and is sometimes called the Sibuya distribution. It has pgf
is a proper distribution and is sometimes called the Sibuya distribution. It has pgf ![]() and no moments exist (see Exercise 6.7). Distributions with no moments are not particularly interesting for modeling claim numbers (unless the right tail is subsequently modified), because then an infinite number of claims is expected. An insurance policy covering such a case might be difficult to price!
and no moments exist (see Exercise 6.7). Distributions with no moments are not particularly interesting for modeling claim numbers (unless the right tail is subsequently modified), because then an infinite number of claims is expected. An insurance policy covering such a case might be difficult to price!
![]()
It is reasonable to ask if there is a “natural” member of the ETNB distribution for the example, that is, one for which the recursion would begin with ![]() rather than
rather than ![]() . The natural value of
. The natural value of ![]() would have to satisfy
would have to satisfy ![]() . This would force one of the two probabilities to be negative and so there is no acceptable solution. It is easy to show that this occurs for any
. This would force one of the two probabilities to be negative and so there is no acceptable solution. It is easy to show that this occurs for any ![]() .
.
There are no other members of the ![]() class beyond the ones just discussed. A summary is given in Table 6.4.
class beyond the ones just discussed. A summary is given in Table 6.4.
Table 6.4 The members of the ![]() class.
class.
| Distributiona | a | b | Parameter space | |
| Poisson | 0 | |||
| ZT Poisson | 0 | 0 | ||
| ZM Poisson | Arbitrary | 0 | ||
| Binomial | ||||
| ZT binomial | 0 | |||
| ZM binomial | Arbitrary | |||
| Negative binomial | ||||
| ETNB | 0 | |||
| ZM ETNB | Arbitrary | |||
| Geometric | 0 | |||
| ZT geometric | 0 | 0 | ||
| ZM geometric | Arbitrary | 0 | ||
| Logarithmic | 0 | |||
| ZM logarithmic | Arbitrary | |||
| a ZT = zero truncated, ZM = zero modified. b Excluding |
||||
6.6.1 Exercises
- 6.4 Show that for the extended truncated negative binomial distribution with any
 and
and  , but
, but  , the successive values of
, the successive values of  given by (6.9) are, for any
given by (6.9) are, for any  , positive and
, positive and 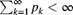 .
. - 6.5 Show that when, in the zero-truncated negative binomial distribution,
 , the pf is as given in (6.10).
, the pf is as given in (6.10). - 6.6 Show that the pgf of the logarithmic distribution is as given in (6.11).
- 6.7 Show that for the Sibuya distribution, which is the ETNB distribution with
 and
and  , the mean does not exist (i.e. the sum that defines the mean does not converge). Because this random variable takes on nonnegative values, this also shows that no other positive moments exist.
, the mean does not exist (i.e. the sum that defines the mean does not converge). Because this random variable takes on nonnegative values, this also shows that no other positive moments exist. - 6.8 If
 , and
, and  is a member of the
is a member of the  class, demonstrate that for
class, demonstrate that for 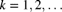 , and
, and 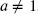 ,
,

where
 .
.

