18
Empirical Bayes Parameter Estimation
18.1 Introduction
In Chapter 17, a modeling methodology was proposed that suggests the use of either the Bayesian or the credibility premium as a way to incorporate past data into the prospective rate. There is a practical problem associated with the use of these models that has not yet been addressed.
In the examples seen so far, we have been able to obtain numerical values for the quantities of interest because the input distributions 
and 
have been assumed to be known. These examples, while useful for illustration of the methodology, can hardly be expected to accurately represent the business of an insurance portfolio. More practical models of necessity involve the use of parameters that must be chosen to ensure a close agreement between the model and reality. Examples of this include: the Poisson–gamma model (Example 17.1), where the gamma parameters 
and 
need to be selected; or the Bühlmann or Bühlmann–Straub parameters 
, and a. The assignment of numerical values to the Bayesian or credibility premium requires that these parameters be replaced by numerical values.
In general, the unknown parameters are those associated with the structure density 
and, hence, we refer to these as structural parameters. The terminology we use follows the Bayesian framework of the previous chapter. Strictly speaking, in the Bayesian context all structural parameters are assumed known and there is no need for estimation. An example is the Poisson–gamma, where our prior information about the structural density is quantified by the choice of 
and 
. For our purposes, this fully Bayesian approach is often unsatisfactory (e.g. when there is little or no prior information available, such as with a new line of insurance) and we may need to use the data at hand to estimate the structural (prior) parameters. This approach is called empirical Bayes estimation.
We refer to the situation in which 
and 
are left largely unspecified (e.g. in the Bühlmann or Bühlmann–Straub models, where only the first two moments need be known) as the nonparametric case. This situation is dealt with in Section 18.2. If 
is assumed to be of parametric form (e.g. Poisson, normal, etc.) but not 
, then we refer to the problem as being of a semiparametric nature and it is considered in Section 18.3. A third, and technically more difficult, case is called fully parametric, where both 
and 
are assumed to be of parametric form. That case is not covered.
This decision as to whether or not to select a parametric model depends partially on the situation at hand and partially on the judgment and knowledge of the person doing the analysis. For example, an analysis based on claim counts might involve the assumption that 
is of Poisson form, whereas the choice of a parametric model for 
may not be reasonable.
Any parametric assumptions should be reflected (as far as possible) in parametric estimation. For example, in the Poisson case, because the mean and variance are equal, the same estimate would normally be used for both. Nonparametric estimators would normally be no more efficient than estimators appropriate for the parametric model selected, assuming that the model selected is appropriate. This notion is relevant for the decision as to whether to select a parametric model.
Finally, nonparametric models have the advantage of being appropriate for a wide variety of situations, a fact that may well eliminate the extra burden of a parametric assumption (often a stronger assumption than is reasonable).
In this section, the data are assumed to be of the following form. For each of 
policyholders, we have the observed losses per unit of exposure 
for 
. The random vectors 
are assumed to be statistically independent (experience of different policyholders is assumed to be independent). The (unknown) risk parameter for the ith policyholder is 
, and it is assumed further that 
are realizations of the i.i.d. random variables 
with structural density 
. For fixed i, the (conditional) random variables 
are assumed to be independent with pf 
.
Two particularly common cases produce this data format. The first is classification ratemaking or experience rating. In either, i indexes the classes or groups and j indexes the individual members. The second case is like the first, where i continues to index the class or group, but now j is the year and the observation is the average loss for that year. An example of the second setting is Meyers [86], where 
employment classifications are studied over 
years. Regardless of the potential settings, we refer to the r entities as policyholders.
There may also be a known exposure vector 
for policyholder i, where 
. If not (and if it is appropriate), we may set 
in what follows for all i and j. For notational convenience, let
be the total past exposure for policyholder i, and let
be the past weighted average loss experience. Furthermore, the total exposure is
and the overall weighted average losses are
The parameters that need to be estimated depend on what is assumed about the distributions 
and 
.
For the Bühlmann–Straub formulation, there are additional quantities of interest. The hypothetical mean (assumed not to depend on j) is
and the process variance is
The structural parameters are
and
The approach is to estimate 
, v, and a (when unknown) from the data. The credibility premium for next year's losses (per exposure unit) for policyholder i is
where
If estimators of 
, and a are denoted by 
, and 
, respectively, then we would replace the credibility premium (18.2) by its estimator
where
Note that, even if 
and 
are unbiased estimators of v and a, the same cannot be said of 
and 
. Finally, the credibility premium to cover all 
exposure units for policyholder i in the next year would be (18.3) multiplied by 
.
18.2 Nonparametric Estimation
In this section, we consider unbiased estimation of 
, v, and a. To illustrate the ideas, let us begin with the following simple Bühlmann-type example.
These estimators might look familiar. Consider a one-factor analysis of variance in which each policyholder represents a treatment. The estimator for v (18.7) is the within (also called the error) mean square. The first term in the estimator for a (18.8) is the between (also called the treatment) mean square divided by n. The hypothesis that all treatments have the same mean is accepted when the between mean square is small relative to the within mean square – that is, when 
is small relative to 
. But that relationship implies 
will be near zero and little credibility will be given to each 
. This is as it should be when the policyholders are essentially identical.
Due to the subtraction in (18.8), it is possible that 
could be negative. When that happens, it is customary to set 
. This case is equivalent to the F-test statistic in the analysis of variance being less than 1, a case that always leads to an acceptance of the hypothesis of equal means.
We now turn to the more general Bühlmann–Straub setup described earlier in this section. We have 
. Thus,
implying that
Finally,
and so an obvious unbiased estimator of 
is
To estimate v and a in the Bühlmann–Straub framework, a more general statistic than that in (18.5) is needed. The following example provides the needed results.
We now return to the problem of estimation of v in the Bühlmann–Straub framework. Clearly, 
and 
for 
. Consider
Condition on 
and use (18.11) with 
and 
. Then, 
, which implies that, unconditionally,
and so 
is unbiased for v for 
. Another unbiased estimator for v is then the weighted average 
, where 
. If we choose weights proportional to 
, we weight the original 
by 
. That is, with 
, we obtain an unbiased estimator of v, namely
We now turn to estimation of a. Recall that, for fixed i, the random variables 
are independent, conditional on 
. Thus,
Then, unconditionally,
To summarize, 
are independent with common mean 
and variances 
. Furthermore, 
. Now, (18.11) may again be used with 
and 
to yield
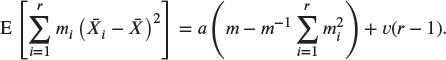
An unbiased estimator for a may be obtained by replacing v by an unbiased estimator 
and “solving” for a. That is, an unbiased estimator of a is
with 
given by (18.13). An alternative form of (18.15) is given in Exercise 18.9.
Some remarks are in order at this point. (Equations 18.9), (18.13), and (18.15) provide unbiased estimators for 
, and a, respectively. They are nonparametric, requiring no distributional assumptions. They are certainly not the only (unbiased) estimators that could be used, and it is possible that 
. In this case, a is likely to be close to zero, and it makes sense to set 
. Furthermore, the ordinary Bühlmann estimators of Example 18.1 are recovered with 
and 
. Finally, these estimators are essentially maximum likelihood estimators in the case where 
and 
are both normally distributed, and thus the estimators have good statistical properties.
There is one problem with the use of the formulas just developed. In the past, the data from the ith policyholder were collected on an exposure of 
. Total losses on all policyholders was 
. If we had charged the credibility premium as previously given, the total premium would have been
It is often desirable for TL to equal TP, because any premium increases that will meet the approval of regulators will be based on the total claim level from past experience. While credibility adjustments make both practical and theoretical sense, it is usually a good idea to keep the total unchanged. Thus, we need
or
or
That is, rather than using (18.9) to compute 
, use a credibility-weighted average of the individual sample means. Either method provides an unbiased estimator (given the 
), but this latter one has the advantage of preserving total claims. It should be noted that when using (18.15), the value of 
from (18.1) should still be used. It can also be derived by least squares arguments. Finally, from Example 18.3 and noting the form of 
in (18.14), the weights in (18.16) provide the smallest unconditional variance for 
.
The preceding analysis assumes that the parameters 
and a are all unknown and need to be estimated, which may not always be the case. Also, it is assumed that 
and 
. If 
so that there is only one exposure unit's experience for policyholder i, it is difficult to obtain information on the process variance 
and, thus, on v. Similarly, if 
, there is only one policyholder, and it is difficult to obtain information on the variance of the hypothetical means a. In these situations, stronger assumptions are needed, such as knowledge of one or more of the parameters (e.g. the pure premium or manual rate 
, discussed in the following) or parametric assumptions that imply functional relationships between the parameters (discussed in Section 18.3).
To illustrate these ideas, suppose, for example, that the manual rate 
may be already known, but estimates of a and v may be needed. In that case, (18.13) can still be used to estimate v as it is unbiased whether 
is known or not. (Why is 
not unbiased for v in this case?) Similarly, (18.15) is still an unbiased estimator for a. However, if 
is known, an alternative unbiased estimator for a is
where 
is given by (18.13). To verify unbiasedness, note that
If there are data on only one policyholder, an approach like this is necessary. Clearly, (18.12) provides an estimator for v based on data from policyholder i alone, and an unbiased estimator for a based on data from policyholder i alone is
which is unbiased because 
and 
.
It is instructive to note that estimation of the parameters a and v based on data from a single policyholder (as in Example 18.5) is not advised unless there is no alternative because the estimators 
and 
have high variability. In particular, we are effectively estimating a from one observation 
. It is strongly suggested that an attempt be made to obtain more data.
18.3 Semiparametric Estimation
In some situations it may be reasonable to assume a parametric form for the conditional distribution 
. The situation at hand may suggest that such an assumption is reasonable or prior information may imply its appropriateness.
For example, in dealing with numbers of claims, it may be reasonable to assume that the number of claims 
for policyholder i in year j is Poisson distributed with mean 
given 
. Thus 
, implying that 
, and so 
in this case. Rather than use (18.13) to estimate v, we could use 
to estimate v.
Note in this case that 
identically, so that only one year's experience per policyholder is needed.
In these examples, there is a functional relationship between the parameters 
, v, and a that follows from the parametric assumptions made, and this often facilitates estimation of parameters.
18.4 Notes and References
In this section, a simple approach is employed to find parameter estimates. No attempt is made to find optimum estimators in the sense of minimum variance. A good deal of research has been done on this problem. For more details and further references, see Goovaerts and Hoogstad [46].
18.5 Exercises
- 18.1 Past claims data on a portfolio of policyholders are given in Table 18.4. Estimate the Bühlmann credibility premium for each of the three policyholders for year 4.
Table 18.4 The data for Exercise 18.1.
Year Policyholder 1 2 3 1 750 800 650 2 625 600 675 3 900 950 850 - 18.2 Past data on a portfolio of group policyholders are given in Table 18.5. Estimate the Bühlmann–Straub credibility premiums to be charged to each group in year 4.
Table 18.5 The data for Exercise 18.2.
Year Policyholder 1 2 3 4 Claims 1 — 20,000 25,000 — Number in group — 100 120 110 Claims 2 19,000 18,000 17,000 — Number in group 90 75 70 60 Claims 3 26,000 30,000 35,000 — Number in group 150 175 180 200 - 18.3 For the situation in Exercise 18.3, estimate the Bühlmann credibility premium for the next year for the policyholder.
- 18.4 Consider the Bühlmann model in Example 18.1.
- Prove that
. - If
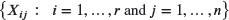are unconditionally independent for all i and j, argue that an unbiased estimator of 
is
- Prove the algebraic identity
- Show that, conditionally,
- Comment on the implications of (b) and (d).
- Prove that
- 18.5 Suppose that the random variables
are independent, with
Define
and 
. Prove that
- 18.6 The distribution of automobile insurance policyholders by number of claims is given in Table 18.6. Assuming a (conditional) Poisson distribution for the number of claims per policyholder, estimate the Bühlmann credibility premiums for the number of claims next year.
Table 18.6 The data for Exercise 18.6.
Number of claims Number of insureds 0 2,500 1 250 2 30 3 5 4 2 Total 2,787 - 18.7 Suppose that, given
, 
are independently geometrically distributed with pf
- Show that
and 
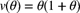. - Prove that
. - Rework Exercise 18.6 assuming a (conditional) geometric distribution.
- Show that
- 18.8 Suppose that
and
Write down the equation satisfied by the mle
of 
for Bühlmann–Straub-type data. - 18.9
- 18.10 (*) In a one-year period, a group of 340 insureds in a high-crime area submit 210 theft claims as given in Table 18.7. Each insured is assumed to have a Poisson distribution for the number of thefts, but the mean of such a distribution may vary from one insured to another. If a particular insured experienced two claims in the observation period, determine the Bühlmann credibility estimate for the number of claims for this insured in the next period.
Table 18.7 The data for Exercise 18.10.
Number of claims Number of insureds 0 200 1 80 2 50 3 10 - 18.11 (*) Three individual policyholders were observed for four years. Policyholder X had claims of 2, 3, 3, and 4. Policyholder Y had claims of 5, 5, 4, and 6. Policyholder Z had claims of 5, 5, 3, and 3. Use nonparametric empirical Bayes estimation to obtain estimated claim amounts for each policyholder in year 5.
- 18.12 (*) Two insureds own delivery vans. Insured A had two vans in year 1 and one claim, two vans in year 2 and one claim, and one van in year 3 with no claims. Insured B had no vans in year 1, three vans in year 2 and two claims, and two vans in year 3 and three claims. The number of claims for insured each year has a Poisson distribution. Use semiparametric empirical Bayes estimation to obtain the estimated number of claims for each insured in year 4.
- 18.13 (*) One hundred policies were in force for a five-year period. Each policyholder has a Poisson distribution for the number of claims, but the parameters may vary. During the five years, 46 policies had no claims, 34 had one claim, 13 had two claims, 5 had three claims, and 2 had four claims. For a policy with three claims in this period, use semiparametric empirical Bayes estimation to estimate the number of claims in year 6 for that policy.
