17
Greatest Accuracy Credibility
17.1 Introduction
In this and Chapter 18, we consider a model-based approach to the solution of the credibility problem. This approach, referred to as greatest accuracy credibility theory, is the outgrowth of a classic 1967 paper by Bühlmann [19]. Many of the ideas are also found in Whitney [131] and Bailey [9].
We return to the basic problem. For a particular policyholder, we have observed n exposure units of past claims ![]() . We have a manual rate
. We have a manual rate ![]() (we no longer use M for the manual rate) applicable to this policyholder, but the past experience indicates that it may not be appropriate (
(we no longer use M for the manual rate) applicable to this policyholder, but the past experience indicates that it may not be appropriate (![]() , as well as
, as well as ![]() , could be quite different from
, could be quite different from ![]() ). This difference raises the question of whether next year's net premium (per exposure unit) should be based on
). This difference raises the question of whether next year's net premium (per exposure unit) should be based on ![]() , on
, on ![]() , or on a combination of the two.
, or on a combination of the two.
The insurer needs to consider the following question: Is the policyholder really different from what has been assumed in the calculation of ![]() , or is it just random chance that is responsible for the difference between
, or is it just random chance that is responsible for the difference between ![]() and
and ![]() ?
?
While it is difficult to definitively answer that question, it is clear that no underwriting system is perfect. The manual rate ![]() has presumably been obtained by (a) evaluation of the underwriting characteristics of the policyholder and (b) assignment of the rate on the basis of inclusion of the policyholder in a rating class. Such a class should include risks with similar underwriting characteristics. In other words, the rating class is viewed as homogeneous with respect to the underwriting characteristics used. Surely, not all risks in the class are truly homogeneous, however. No matter how detailed the underwriting procedure, there still remains some heterogeneity with respect to risk characteristics within the rating class (good and bad risks, relatively speaking).
has presumably been obtained by (a) evaluation of the underwriting characteristics of the policyholder and (b) assignment of the rate on the basis of inclusion of the policyholder in a rating class. Such a class should include risks with similar underwriting characteristics. In other words, the rating class is viewed as homogeneous with respect to the underwriting characteristics used. Surely, not all risks in the class are truly homogeneous, however. No matter how detailed the underwriting procedure, there still remains some heterogeneity with respect to risk characteristics within the rating class (good and bad risks, relatively speaking).
Thus, it is possible that the given policyholder may be different from what has been assumed. If this is the case, how should an appropriate rate for the policyholder be determined?
To proceed, let us assume that the risk level of each policyholder in the rating class may be characterized by a risk parameter ![]() (possibly vector valued), but that the value of
(possibly vector valued), but that the value of ![]() varies by policyholder. This assumption allows us to quantify the differences between policyholders with respect to the risk characteristics. Because all observable underwriting characteristics have already been used,
varies by policyholder. This assumption allows us to quantify the differences between policyholders with respect to the risk characteristics. Because all observable underwriting characteristics have already been used, ![]() may be viewed as representative of the residual, unobserved factors that affect the risk level. Consequently, we shall assume the existence of
may be viewed as representative of the residual, unobserved factors that affect the risk level. Consequently, we shall assume the existence of ![]() , but we shall further assume that it is not observable and that we can never know its true value.
, but we shall further assume that it is not observable and that we can never know its true value.
Because ![]() varies by policyholder, there is a probability distribution with pf
varies by policyholder, there is a probability distribution with pf ![]() of these values across the rating class. Thus, if
of these values across the rating class. Thus, if ![]() is a scalar parameter, the cumulative distribution function
is a scalar parameter, the cumulative distribution function ![]() may be interpreted as the proportion of policyholders in the rating class with risk parameter
may be interpreted as the proportion of policyholders in the rating class with risk parameter ![]() less than or equal to
less than or equal to ![]() . (In statistical terms,
. (In statistical terms, ![]() is a random variable with distribution function
is a random variable with distribution function ![]() ) Stated another way,
) Stated another way, ![]() represents the probability that a policyholder picked at random from the rating class has a risk parameter less than or equal to
represents the probability that a policyholder picked at random from the rating class has a risk parameter less than or equal to ![]() (to accommodate the possibility of new insureds, we slightly generalize the “rating class” interpretation to include the population of all potential risks, whether insured or not).
(to accommodate the possibility of new insureds, we slightly generalize the “rating class” interpretation to include the population of all potential risks, whether insured or not).
While the ![]() value associated with an individual policyholder is not (and cannot be) known, we assume (for this chapter) that
value associated with an individual policyholder is not (and cannot be) known, we assume (for this chapter) that ![]() is known. That is, the structure of the risk characteristics within the population is known. This assumption can be relaxed, and we shall decide later how to estimate the relevant characteristics of
is known. That is, the structure of the risk characteristics within the population is known. This assumption can be relaxed, and we shall decide later how to estimate the relevant characteristics of ![]() .
.
Because risk levels vary within the population, it is clear that the experience of the policyholder varies in a systematic way with ![]() . Imagine that the experience of a policyholder picked (at random) from the population arises from a two-stage process. First, the risk parameter
. Imagine that the experience of a policyholder picked (at random) from the population arises from a two-stage process. First, the risk parameter ![]() is selected from the distribution
is selected from the distribution ![]() . Then the claims or losses X arise from the conditional distribution of X given
. Then the claims or losses X arise from the conditional distribution of X given ![]() ,
, ![]() . Thus the experience varies with
. Thus the experience varies with ![]() via the distribution given the risk parameter
via the distribution given the risk parameter ![]() . The distribution of claims thus differs from policyholder to policyholder to reflect the differences in the risk parameters.
. The distribution of claims thus differs from policyholder to policyholder to reflect the differences in the risk parameters.
![]()
![]()
![]()
17.2 Conditional Distributions and Expectation
The formulation of the problem just presented involves the use of conditional distributions, given the risk parameter ![]() of the insured. Subsequent analyses of mathematical models of this nature will be seen to require a good working knowledge of conditional distributions and conditional expectation. A discussion of these topics is now presented.
of the insured. Subsequent analyses of mathematical models of this nature will be seen to require a good working knowledge of conditional distributions and conditional expectation. A discussion of these topics is now presented.
Much of the material is of a review nature and, hence, may be quickly glossed over if you have a good background in probability. Nevertheless, there may be some material not seen before, and so this section should not be completely ignored.
Suppose that X and Y are two random variables with joint probability function (pf) or probability density function (pdf)2 ![]() and marginal pfs
and marginal pfs ![]() and
and ![]() , respectively. The conditional pf of X given that
, respectively. The conditional pf of X given that ![]() is
is
If X and Y are discrete random variables, then ![]() is the conditional probability of the event
is the conditional probability of the event ![]() under the hypothesis that
under the hypothesis that ![]() . If X and Y are continuous, then
. If X and Y are continuous, then ![]() may be interpreted as a definition. When X and Y are independent random variables,
may be interpreted as a definition. When X and Y are independent random variables,
and, in this case,
We observe that the conditional and marginal distributions of X are identical.
Note that
demonstrating that joint distributions may be constructed from products of conditional and marginal distributions. Because the marginal distribution of X may be obtained by integrating (or summing) y out of the joint distribution,
we find that
Formula (17.1) has an interesting interpretation as a mixed distribution (see Section 5.2.4). Assume that the conditional distribution ![]() is one of the usual parametric distributions, where y is the realization of a random parameter Y with distribution
is one of the usual parametric distributions, where y is the realization of a random parameter Y with distribution ![]() . Section 6.3 shows that if, given
. Section 6.3 shows that if, given ![]() , X has a Poisson distribution with mean
, X has a Poisson distribution with mean ![]() and
and ![]() has a gamma distribution, then the marginal distribution of X will be negative binomial. Also, Example 5.5 shows that if
has a gamma distribution, then the marginal distribution of X will be negative binomial. Also, Example 5.5 shows that if ![]() has a normal distribution with mean
has a normal distribution with mean ![]() and variance v and
and variance v and ![]() has a normal distribution with mean
has a normal distribution with mean ![]() and variance a, then the marginal distribution of X is normal with mean
and variance a, then the marginal distribution of X is normal with mean ![]() and variance
and variance ![]() .
.
Note that the roles of X and Y can be interchanged, yielding
because both sides of this equation equal the joint distribution of X and Y. Division by ![]() yields Bayes' theorem, namely
yields Bayes' theorem, namely
We now turn our attention to conditional expectation. Consider the conditional pf of X given that ![]() ,
, ![]() . Clearly, this is a valid probability distribution, and its mean is denoted by
. Clearly, this is a valid probability distribution, and its mean is denoted by
with the integral replaced by a sum in the discrete case.3 Clearly, (17.2) is a function of y, and it is often of interest to view this conditional expectation as a random variable obtained by replacing y by Y in the right-hand side of (17.2). Thus we can write ![]() instead of the left-hand side of (17.2), and so
instead of the left-hand side of (17.2), and so ![]() is itself a random variable because it is a function of the random variable Y. The expectation of
is itself a random variable because it is a function of the random variable Y. The expectation of ![]() is given by
is given by
Equation (17.3) can be proved using (17.2) as follows:

with a similar derivation in the discrete case.
![]()
It is often convenient to replace X by an arbitrary function ![]() in (17.2), yielding the more general definition
in (17.2), yielding the more general definition
Similarly, ![]() is the conditional expectation viewed as a random variable that is a function of Y. Then, (17.3) generalizes to
is the conditional expectation viewed as a random variable that is a function of Y. Then, (17.3) generalizes to
To see (17.4), note that

If we choose ![]() , then its expected value, based on the conditional distribution of X given Y, is the variance of this conditional distribution,
, then its expected value, based on the conditional distribution of X given Y, is the variance of this conditional distribution,
Clearly, (17.5) is a function of the random variable Y.
It is instructive now to analyze the variance of X where X and Y are two random variables. To begin, note that (17.5) may be written as
Thus,

Also, because ![]() , we may use
, we may use ![]() to obtain
to obtain

Thus,

Finally, we have established the important formula
Formula (17.6) states that the variance of X is composed of the sum of two parts: the mean of the conditional variance plus the variance of the conditional mean.
![]()
![]()
17.3 The Bayesian Methodology
Continue to assume that the distribution of the risk characteristics in the population may be represented by ![]() , and the experience of a particular policyholder with risk parameter
, and the experience of a particular policyholder with risk parameter ![]() arises from the conditional distribution
arises from the conditional distribution ![]() of claims or losses, given
of claims or losses, given ![]() .
.
We now return to the problem introduced in Section 16.2. That is, for a particular policyholder, we have observed ![]() , where
, where ![]() and
and ![]() , and are interested in setting a rate to cover
, and are interested in setting a rate to cover ![]() . We assume that the risk parameter associated with the policyholder is
. We assume that the risk parameter associated with the policyholder is ![]() (which is unknown). Furthermore, the experience of the policyholder corresponding to different exposure periods is assumed to be independent. In statistical terms, conditional on
(which is unknown). Furthermore, the experience of the policyholder corresponding to different exposure periods is assumed to be independent. In statistical terms, conditional on ![]() , the claims or losses
, the claims or losses ![]() are independent (although not necessarily identically distributed).
are independent (although not necessarily identically distributed).
Let ![]() have conditional pf
have conditional pf
Note that, if the ![]() are identically distributed (conditional on
are identically distributed (conditional on ![]() ), then
), then ![]() does not depend on j. Ideally, we are interested in the conditional distribution of
does not depend on j. Ideally, we are interested in the conditional distribution of ![]() , given
, given ![]() , in order to predict the claims experience
, in order to predict the claims experience ![]() of the same policyholder (whose value of
of the same policyholder (whose value of ![]() has been assumed not to have changed). If we knew
has been assumed not to have changed). If we knew ![]() , we could use
, we could use ![]() . Unfortunately, we do not know
. Unfortunately, we do not know ![]() , but we do know x for the same policyholder. The obvious next step is to condition on x rather than
, but we do know x for the same policyholder. The obvious next step is to condition on x rather than ![]() . Consequently, we calculate the conditional distribution of
. Consequently, we calculate the conditional distribution of ![]() given
given ![]() , termed the predictive distribution, as defined in Chapter 13.
, termed the predictive distribution, as defined in Chapter 13.
The predictive distribution of ![]() given
given ![]() is the relevant distribution for risk analysis, management, and decision making. It combines the uncertainty about the claims losses with that of the parameters associated with the risk process.
is the relevant distribution for risk analysis, management, and decision making. It combines the uncertainty about the claims losses with that of the parameters associated with the risk process.
Here, we repeat the development in Chapter 13, noting that if ![]() has a discrete distribution, the integrals are replaced by sums. Because the
has a discrete distribution, the integrals are replaced by sums. Because the ![]() are independent conditional on
are independent conditional on ![]() , we have
, we have

The joint distribution of X is thus the marginal distribution obtained by integrating ![]() out, that is,
out, that is,
Similarly, the joint distribution of ![]() is the right-hand side of (17.7) with n replaced by
is the right-hand side of (17.7) with n replaced by ![]() in the product. Finally, the conditional density of
in the product. Finally, the conditional density of ![]() given
given ![]() is the joint density of
is the joint density of ![]() divided by that of X, namely
divided by that of X, namely
There is a hidden mathematical structure underlying (17.8) that may be exploited. The posterior density of ![]() given X is
given X is
In other words, ![]() , and substitution in the numerator of (17.8) yields
, and substitution in the numerator of (17.8) yields
Equation (17.10) provides the additional insight that the conditional distribution of ![]() given X may be viewed as a mixture distribution, with the mixing distribution being the posterior distribution
given X may be viewed as a mixture distribution, with the mixing distribution being the posterior distribution ![]() .
.
The posterior distribution combines and summarizes the information about ![]() contained in the prior distribution and the likelihood, and consequently (17.10) reflects this information. As noted in Theorem 13.18, the posterior distribution admits a convenient form when the likelihood is derived from the linear exponential family and
contained in the prior distribution and the likelihood, and consequently (17.10) reflects this information. As noted in Theorem 13.18, the posterior distribution admits a convenient form when the likelihood is derived from the linear exponential family and ![]() is the natural conjugate prior. When both are in place, there is an easy method to evaluate the conditional distribution of
is the natural conjugate prior. When both are in place, there is an easy method to evaluate the conditional distribution of ![]() given X.
given X.
![]()
![]()
Note that the posterior distribution is of the same type (gamma) as the prior distribution. The concept of a conjugate prior distribution is introduced in Section 13.3. This result also implies that ![]() is a mixture distribution with a simple mixing distribution, facilitating evaluation of the density of
is a mixture distribution with a simple mixing distribution, facilitating evaluation of the density of ![]() . Further examples of this idea are found in the exercises at the end of this section.
. Further examples of this idea are found in the exercises at the end of this section.
To return to the original problem, we have observed ![]() for a particular policyholder and we wish to predict
for a particular policyholder and we wish to predict ![]() (or its mean). An obvious choice would be the hypothetical mean (or individual premium)
(or its mean). An obvious choice would be the hypothetical mean (or individual premium)
if we knew ![]() . Note that replacement of
. Note that replacement of ![]() by
by ![]() in (17.11) yields, on taking the expectation,
in (17.11) yields, on taking the expectation,
so that the pure, or collective, premium is the mean of the hypothetical means. This is the premium we would use if we knew nothing about the individual. It does not depend on the individual's risk parameter, ![]() ; nor does it use x, the data collected from the individual. Because
; nor does it use x, the data collected from the individual. Because ![]() is unknown, the best we can do is try to use the data, which suggest the use of the Bayesian premium (the mean of the predictive distribution):
is unknown, the best we can do is try to use the data, which suggest the use of the Bayesian premium (the mean of the predictive distribution):
A computationally more convenient form is
In other words, the Bayesian premium is the expected value of the hypothetical means, with expectation taken over the posterior distribution ![]() . Recall that in the discrete case, the integrals are replaced by sums. To prove (17.13 ), we see from (17.10) that
. Recall that in the discrete case, the integrals are replaced by sums. To prove (17.13 ), we see from (17.10) that

![]()
As expected, the revised value based on two observations is between the prior value (0.475) based on no data and the value based only on the data (0.5).
![]()
![]()
Example 17.12 is one where the random variables do not have identical distributions.
![]()
In each of Examples 17.11 and 17.12, the Bayesian estimate was a weighted average of the sample mean ![]() and the pure premium
and the pure premium ![]() . This result is appealing from a credibility standpoint. Furthermore, the credibility factor Z in each case is an increasing function of the number of exposure units. The greater the amount of past data observed, the closer Z is to 1, consistent with our intuition.
. This result is appealing from a credibility standpoint. Furthermore, the credibility factor Z in each case is an increasing function of the number of exposure units. The greater the amount of past data observed, the closer Z is to 1, consistent with our intuition.
17.4 The Credibility Premium
In Section 17.3, a systematic approach is suggested for treatment of the past data of a particular policyholder. Ideally, rather than the pure premium ![]() , we would like to charge the individual premium (or hypothetical mean)
, we would like to charge the individual premium (or hypothetical mean) ![]() , where
, where ![]() is the (hypothetical) parameter associated with the policyholder. Because
is the (hypothetical) parameter associated with the policyholder. Because ![]() is unknown, the hypothetical mean is impossible to determine, but we could instead condition on x, the past data from the policyholder. This leads to the Bayesian premium
is unknown, the hypothetical mean is impossible to determine, but we could instead condition on x, the past data from the policyholder. This leads to the Bayesian premium ![]() .
.
The major challenge with this approach is that it may be difficult to evaluate the Bayesian premium. Of course, in simple examples such as those in Section 17.3, the Bayesian premium is not difficult to evaluate numerically. But these examples can hardly be expected to capture the essential features of a realistic insurance scenario. More realistic models may well introduce analytic difficulties with respect to evaluation of ![]() , whether we use (17.12) or (17.13). Often, numerical integration may be required. There are exceptions, such as Examples 17.11 and 17.12.
, whether we use (17.12) or (17.13). Often, numerical integration may be required. There are exceptions, such as Examples 17.11 and 17.12.
We now present an alternative suggested by Bühlmann [19] in 1967. Recall the basic problem. We wish to use the conditional distribution ![]() or the hypothetical mean
or the hypothetical mean ![]() for estimation of next year's claims. Because we have observed x, one suggestion is to approximate
for estimation of next year's claims. Because we have observed x, one suggestion is to approximate ![]() by a linear function of the past data. (After all, the formula
by a linear function of the past data. (After all, the formula ![]() is of this form.) Thus, let us restrict ourselves to estimators of the form
is of this form.) Thus, let us restrict ourselves to estimators of the form ![]() , where
, where ![]() need to be chosen. To this end, we choose the
need to be chosen. To this end, we choose the ![]() s to minimize expected squared-error loss, that is,
s to minimize expected squared-error loss, that is,
and the expectation is over the joint distribution of ![]() and
and ![]() . That is, the squared error is averaged over all possible values of
. That is, the squared error is averaged over all possible values of ![]() and all possible observations. To minimize Q, we take derivatives. Thus,
and all possible observations. To minimize Q, we take derivatives. Thus,

We shall denote by ![]() the values of
the values of ![]() that minimize (17.14). Then, equating
that minimize (17.14). Then, equating ![]() to 0 yields
to 0 yields

But ![]() , and so
, and so ![]() implies that
implies that
Equation (17.15) may be termed the unbiasedness equation because it requires that the estimate ![]() be unbiased for
be unbiased for ![]() . However, the credibility estimate may be biased as an estimator of
. However, the credibility estimate may be biased as an estimator of ![]() , the quantity we are trying to estimate. This bias will average out over the members of
, the quantity we are trying to estimate. This bias will average out over the members of ![]() . By accepting this bias, we are able to reduce the overall MSE. For
. By accepting this bias, we are able to reduce the overall MSE. For ![]() , we have
, we have

and setting this expression equal to zero yields

The left-hand side of this equation may be reexpressed as

where the second from last step follows by independence of ![]() and
and ![]() conditional on
conditional on ![]() . Thus
. Thus ![]() implies
implies
Next, multiply (17.15) by ![]() and subtract from (17.16) to obtain
and subtract from (17.16) to obtain
Equation (17.15) and the n equations (17.17) together are called the normal equations. These equations may be solved for ![]() to yield the credibility premium
to yield the credibility premium
While it is straightforward to express the solution ![]() to the normal equations in matrix notation (if the covariance matrix of the
to the normal equations in matrix notation (if the covariance matrix of the ![]() is nonsingular), we shall be content with solutions for some special cases.
is nonsingular), we shall be content with solutions for some special cases.
Note that exactly one of the terms on the right-hand side of (17.17) is a variance term, that is, ![]() . The other
. The other ![]() terms are true covariance terms.
terms are true covariance terms.
As an added bonus, the values ![]() also minimize
also minimize
and
To see this, differentiate (17.19) or (17.20) with respect to ![]() and observe that the solutions still satisfy the normal equations (17.15) and (17.17). Thus the credibility premium (17.18) is the best linear estimator of each of the hypothetical mean
and observe that the solutions still satisfy the normal equations (17.15) and (17.17). Thus the credibility premium (17.18) is the best linear estimator of each of the hypothetical mean ![]() , the Bayesian premium
, the Bayesian premium ![]() , and
, and ![]() .
.
![]()
We now turn to some models that specify the conditional means and variances of ![]() and, hence, the means
and, hence, the means ![]() , variances
, variances ![]() , and covariances
, and covariances ![]() .
.
17.5 The Bühlmann Model
The simplest credibility model, the Bühlmann model, specifies that, for each policyholder (conditional on ![]() ), past losses
), past losses ![]() have the same mean and variance and are i.i.d. conditional on
have the same mean and variance and are i.i.d. conditional on ![]() .
.
Thus, define
and
As discussed previously, ![]() is referred to as the hypothetical mean, whereas
is referred to as the hypothetical mean, whereas ![]() is called the process variance. Define
is called the process variance. Define
and
The quantity ![]() in (17.21) is the expected value of the hypothetical means, v in (17.22) is the expected value of the process variance, and a in (17.23) is the variance of the hypothetical means. Note that
in (17.21) is the expected value of the hypothetical means, v in (17.22) is the expected value of the process variance, and a in (17.23) is the variance of the hypothetical means. Note that ![]() is the estimate to use if we have no information about
is the estimate to use if we have no information about ![]() (and thus no information about
(and thus no information about ![]() ). It will also be referred to as the collective premium.
). It will also be referred to as the collective premium.
The mean, variance, and covariance of the ![]() may now be obtained. First,
may now be obtained. First,
Second,

Finally, for ![]() ,
,
This result is exactly of the form of Example 17.13 with parameters ![]() , and
, and ![]() . Thus the credibility premium is
. Thus the credibility premium is
where
and
The credibility factor Z in (17.28) with k given by (17.29) is referred to as the Bühlmann credibility factor. Note that (17.27) is of the form (16.7), and (17.28) is exactly (16.8). Now, however, we know how to obtain k, namely, from (17.29).
Formula (17.27) has many appealing features. First, the credibility premium (17.27) is a weighted average of the sample mean ![]() and the collective premium
and the collective premium ![]() , a formula we find desirable. Furthermore, Z approaches 1 as n increases, giving more credit to
, a formula we find desirable. Furthermore, Z approaches 1 as n increases, giving more credit to ![]() rather than
rather than ![]() as more past data accumulate, a feature that agrees with intuition. Also, if the population is fairly homogeneous with respect to the risk parameter
as more past data accumulate, a feature that agrees with intuition. Also, if the population is fairly homogeneous with respect to the risk parameter ![]() , then (relatively speaking) the hypothetical means
, then (relatively speaking) the hypothetical means ![]() do not vary greatly with
do not vary greatly with ![]() (i.e. they are close in value) and hence have small variability. Thus, a is small relative to v, that is, k is large and Z is closer to zero. This observation agrees with intuition because, for a homogeneous population, the overall mean
(i.e. they are close in value) and hence have small variability. Thus, a is small relative to v, that is, k is large and Z is closer to zero. This observation agrees with intuition because, for a homogeneous population, the overall mean ![]() is of more value in helping to predict next year's claims for a particular policyholder. Conversely, for a heterogeneous population, the hypothetical means
is of more value in helping to predict next year's claims for a particular policyholder. Conversely, for a heterogeneous population, the hypothetical means ![]() are more variable, that is, a is large and k is small, and so Z is closer to 1. Again this observation makes sense because, in a heterogeneous population, the experience of other policyholders is of less value in predicting the future experience of a particular policyholder than is the past experience of that policyholder.
are more variable, that is, a is large and k is small, and so Z is closer to 1. Again this observation makes sense because, in a heterogeneous population, the experience of other policyholders is of less value in predicting the future experience of a particular policyholder than is the past experience of that policyholder.
We now present some examples.
![]()
![]()
![]()
An alternative analysis for this problem could have started with a single observation of ![]() . From the assumptions of the problem, S has a mean of
. From the assumptions of the problem, S has a mean of ![]() and a variance of
and a variance of ![]() . While it is true that S has a gamma distribution, that information is not needed because the Bühlmann approximation requires only moments. Following the preceding calculations,
. While it is true that S has a gamma distribution, that information is not needed because the Bühlmann approximation requires only moments. Following the preceding calculations,
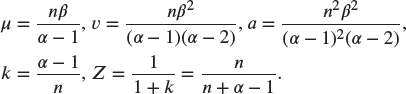
The key is to note that in calculating Z the sample size is now 1, reflecting the single observation of S. Because ![]() , the Bühlmann estimate is
, the Bühlmann estimate is
which is n times the previous answer. That is because we are now estimating the next value of S rather than the next value of X. However, the credibility factor itself (i.e. Z) is the same whether we are predicting ![]() or the next value of S.
or the next value of S.
17.6 The Bühlmann–Straub Model
The Bühlmann model is the simplest of the credibility models because it effectively requires that the past claims experience of a policyholder comprise i.i.d. components with respect to each past year. An important practical difficulty with this assumption is that it does not allow for variations in exposure or size.
For example, what if the first year's claims experience of a policyholder reflected only a portion of a year due to an unusual policyholder anniversary? What if a benefit change occurred part way through a policy year? For group insurance, what if the size of the group changed over time?
To handle these variations, we consider the following generalization of the Bühlmann model. Assume that ![]() are independent, conditional on
are independent, conditional on ![]() , with common mean (as before)
, with common mean (as before)
but with conditional variances
where ![]() is a known constant measuring exposure. Note that
is a known constant measuring exposure. Note that ![]() need only be proportional to the size of the risk. This model would be appropriate if each
need only be proportional to the size of the risk. This model would be appropriate if each ![]() were the average of
were the average of ![]() independent (conditional on
independent (conditional on ![]() ) random variables each with mean
) random variables each with mean ![]() and variance
and variance ![]() . In the preceding situations,
. In the preceding situations, ![]() could be the number of months the policy was in force in past year j, or the number of individuals in the group in past year j, or the amount of premium income for the policy in past year j.
could be the number of months the policy was in force in past year j, or the number of individuals in the group in past year j, or the amount of premium income for the policy in past year j.
As in the Bühlmann model, let
and
Then, for the unconditional moments, from (17.24) ![]() , and from (17.26)
, and from (17.26) ![]() , but
, but

To obtain the credibility premium (17.18), we solve the normal equations (17.15) and (17.17) to obtain ![]() . For notational convenience, define
. For notational convenience, define
to be the total exposure. Then, using (17.24), the unbiasedness equation (17.15) becomes

which implies
For ![]() , (17.17) becomes
, (17.17) becomes
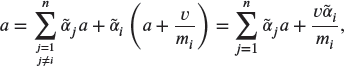
which may be rewritten as
Then, using (17.30) and (17.31),

and so
As a result,
The credibility premium (17.18) becomes
where, with ![]() from (17.29),
from (17.29),
and
Clearly, the credibility premium (17.32) is still of the form (16.7). In this case, m is the total exposure associated with the policyholder, and the Bühlmann–Straub credibility factor Z depends on m. Furthermore, ![]() is a weighted average of the
is a weighted average of the ![]() , with weights proportional to
, with weights proportional to ![]() . Following the group interpretation,
. Following the group interpretation, ![]() is the average loss of the
is the average loss of the ![]() group members in year j, and so
group members in year j, and so ![]() is the total loss of the group in year j. Then,
is the total loss of the group in year j. Then, ![]() is the overall average loss per group member over the n years. The credibility premium to be charged to the group in year
is the overall average loss per group member over the n years. The credibility premium to be charged to the group in year ![]() would thus be
would thus be ![]() for
for ![]() members in the next year.
members in the next year.
Had we known that (17.33) would be the correct weighting of the ![]() to receive the credibility weight Z, the rest would have been easy. For the single observation
to receive the credibility weight Z, the rest would have been easy. For the single observation ![]() , the process variance is
, the process variance is

and so the expected process variance is ![]() . The variance of the hypothetical means is still a, and therefore
. The variance of the hypothetical means is still a, and therefore ![]() . There is only one observation of
. There is only one observation of ![]() , and so the credibility factor is
, and so the credibility factor is
as before. Equation (17.33) should not have been surprising because the weights are simply inversely proportional to the (conditional) variance of each ![]() .
.
![]()
The assumptions underlying the Bühlmann–Straub model may be too restrictive to represent reality. In a 1967 paper, Hewitt [54] observed that large risks do not behave the same as an independent aggregation of small risks and, in fact, are more variable than would be indicated by independence. A model that reflects this observation is created in the following example.
![]()
Another generalization is provided by letting the variance of ![]() depend on the exposure, which may be reasonable if we believe that the extent to which a given risk's propensity to produce claims that differ from the mean is related to its size. For example, larger risks may be underwritten more carefully. In this case, extreme variations from the mean are less likely because we ensure that the risk not only meets the underwriting requirements but also appears to be exactly what it claims to be.
depend on the exposure, which may be reasonable if we believe that the extent to which a given risk's propensity to produce claims that differ from the mean is related to its size. For example, larger risks may be underwritten more carefully. In this case, extreme variations from the mean are less likely because we ensure that the risk not only meets the underwriting requirements but also appears to be exactly what it claims to be.
![]()
17.7 Exact Credibility
In Examples 17.15–17.17, we found that the credibility premium and the Bayesian premium are equal. From (17.19), we may view the credibility premium as the best linear approximation to the Bayesian premium in the sense of squared-error loss. In these examples, the approximation is exact because the two premiums are equal. The term exact credibility is used to describe the situation in which the credibility premium equals the Bayesian premium.
At first glance, it appears to be unnecessary to discuss the existence and finiteness of the credibility premium in this context, because exact credibility as defined is clearly not possible otherwise. However, in what follows, there are some technical issues to be considered, and their treatment is clearer if it is tacitly remembered that the credibility premium must be well defined, which requires that ![]() ,
, ![]() , and
, and ![]() , as is obvious from the normal equations (17.15) and (17.17). Exact credibility typically occurs in Bühlmann (and Bühlmann–Straub) situations involving linear exponential family members and their conjugate priors. It is clear that the existence of the credibility premium requires that the structural parameters
, as is obvious from the normal equations (17.15) and (17.17). Exact credibility typically occurs in Bühlmann (and Bühlmann–Straub) situations involving linear exponential family members and their conjugate priors. It is clear that the existence of the credibility premium requires that the structural parameters ![]() ,
, ![]() , and
, and ![]() be finite.
be finite.
Consider ![]() in this situation. Recall from (5.8) that, for the linear exponential family, the mean is
in this situation. Recall from (5.8) that, for the linear exponential family, the mean is
and the conjugate prior pdf is, from Theorem 13.18, given by
where the interval of support ![]() is explicitly identified. Also, for now,
is explicitly identified. Also, for now, ![]() and k should be viewed as known parameters associated with the prior pdf
and k should be viewed as known parameters associated with the prior pdf ![]() . To determine
. To determine ![]() , note that from (17.36) it follows that
, note that from (17.36) it follows that
and differentiating with respect to ![]() yields
yields

Multiplication by ![]() results in, using (17.35),
results in, using (17.35),
Next, integrate both sides of (17.37) with respect to ![]() over the interval
over the interval ![]() , to obtain
, to obtain
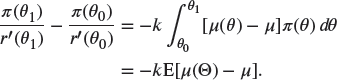
Therefore, it follows that
Note that, if
then
demonstrating that the choice of the symbol ![]() in (17.36) is not coincidental. If (17.40) holds, as is often the case, it is normally because both sides of (17.39) are equal to zero. Regardless, it is possible to have
in (17.36) is not coincidental. If (17.40) holds, as is often the case, it is normally because both sides of (17.39) are equal to zero. Regardless, it is possible to have ![]() but
but ![]() . Also,
. Also, ![]() may result if either
may result if either ![]() or
or ![]() fails to be finite.
fails to be finite.
Next, consider the posterior distribution in the Bühlmann situation with

and ![]() given by (17.36). From Theorem 13.18 , the posterior pdf is
given by (17.36). From Theorem 13.18 , the posterior pdf is
with
and
Because (17.41) is of the same form as (17.36), the Bayesian premium (17.13) is
with ![]() given by (17.43). Because
given by (17.43). Because ![]() is a linear function of the
is a linear function of the ![]() , the same is true of the Bayesian premium if
, the same is true of the Bayesian premium if
that is, (17.45) implies that (17.44) becomes
Clearly, for (17.45) to hold for all vectors x, both sides should be equal to zero. Also, note that (17.46) is of the form (16.7).
To summarize, posterior linearity of the Bayesian premium results (i.e. (17.46) holds) if (17.45) is true (usually with both sides equal to zero). It is instructive to note that posterior linearity of the Bayesian premium may occur even if ![]() . However, as long as the credibility premium is well defined (all three of
. However, as long as the credibility premium is well defined (all three of ![]() ,
, ![]() , and
, and ![]() are finite), the posterior linearity of the Bayesian premium implies equality with the credibility premium, that is, exact credibility. To see this equivalence, note that, if the Bayesian premium is a linear function of
are finite), the posterior linearity of the Bayesian premium implies equality with the credibility premium, that is, exact credibility. To see this equivalence, note that, if the Bayesian premium is a linear function of ![]() , that is,
, that is,
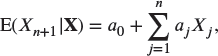
then it is clear that in (17.19) the quantity ![]() attains its minimum value of zero with
attains its minimum value of zero with ![]() for
for ![]() . Thus the credibility premium is
. Thus the credibility premium is ![]() , and credibility is exact.
, and credibility is exact.
The following example clarifies these concepts.
![]()
There is one last technical point worth noting. It was mentioned previously that the choice of the symbol ![]() as a parameter associated with the prior pdf
as a parameter associated with the prior pdf ![]() is not a coincidence because it is often the case that
is not a coincidence because it is often the case that ![]() . A similar comment applies to the parameter k. Because
. A similar comment applies to the parameter k. Because ![]() from (5.9), it follows from (17.37) and the product rule for differentiation that
from (5.9), it follows from (17.37) and the product rule for differentiation that

Integrating with respect to ![]() over
over ![]() yields
yields

and solving for k yields
If, in addition, (17.39) holds, then (17.40) holds, and (17.51) simplifies to

in turn simplifying to the well-known result ![]() if
if
which typically holds with both sides equal to zero.
17.8 Notes and References
In this section, one of the two major criticisms of limited fluctuation credibility has been addressed. Through the use of the variance of the hypothetical means, we now have a means of relating the mean of the group of interest, ![]() , to the manual, or collective, premium,
, to the manual, or collective, premium, ![]() . The development is also mathematically sound in that the results follow directly from a specific model and objective. We have also seen that the additional restriction of a linear solution is not as bad as it might be in that we still often obtain the exact Bayesian solution. There has subsequently been a great deal of effort expended to generalize the model. With a sound basis for obtaining a credibility premium, we have but one remaining obstacle: how to numerically estimate the quantities a and v in the Bühlmann formulation, or how to specify the prior distribution in the Bayesian formulation. Those matters are addressed in Chapter 18.
. The development is also mathematically sound in that the results follow directly from a specific model and objective. We have also seen that the additional restriction of a linear solution is not as bad as it might be in that we still often obtain the exact Bayesian solution. There has subsequently been a great deal of effort expended to generalize the model. With a sound basis for obtaining a credibility premium, we have but one remaining obstacle: how to numerically estimate the quantities a and v in the Bühlmann formulation, or how to specify the prior distribution in the Bayesian formulation. Those matters are addressed in Chapter 18.
A historical review of credibility theory including a description of the limited fluctuation and greatest accuracy approaches is provided by Norberg [94]. Since the classic paper of Bühlmann [19], there has developed a vast literature on credibility theory in the actuarial literature. Other elementary introductions are given by Herzog [52] and Waters [130]. Other more advanced treatments are Goovaerts and Hoogstad [46] and Sundt [118]. An important generalization of the Bühlmann–Straub model is the Hachemeister [48] regression model, which is not discussed here. See also Klugman [71]. The material on exact credibility is motivated by Jewell [62]. See also Ericson [36]. A special issue of Insurance: Abstracts and Reviews (Sundt [117]) contains an extensive list of papers on credibility.
17.9 Exercises
- 17.1 Suppose that X and Z are independent Poisson random variables with means
 and
and  , respectively. Let
, respectively. Let  . Demonstrate that
. Demonstrate that  is binomial.
is binomial. - 17.2 Suppose X is binomially distributed with parameters
 and p, that is,
and p, that is,

Suppose also that Z is binomially distributed with parameters
 and p independently of X. Then,
and p independently of X. Then,  is binomially distributed with parameters
is binomially distributed with parameters  and p. Demonstrate that
and p. Demonstrate that  has the hypergeometric distribution.
has the hypergeometric distribution. - 17.3 Consider a compound Poisson distribution with Poisson mean
 , where
, where  with
with  and
and  . Determine the mean and variance of X.
. Determine the mean and variance of X. - 17.4 Let X and Y have joint probability distribution as given in Table 17.2.
- Compute the marginal distributions of X and Y.
- Compute the conditional distribution of X given
 for
for  .
. - Compute
 ,
,  , and
, and  for
for  .
. - Compute
 and
and  using (17.3), (17.6), and (c).
using (17.3), (17.6), and (c).
Table 17.2 The data for Exercise 17.4.
y x 0 1 2 0 0.20 0 0.10 1 0 0.15 0.25 2 0.05 0.15 0.10 - 17.5 Suppose that X and Y are two random variables with bivariate normal joint density function

Show the following:
- The conditional density function is
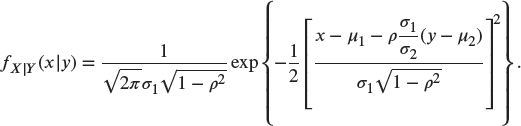
Hence,
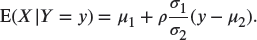
- The marginal pdf is

- The variables X and Y are independent if and only if
 .
.
- The conditional density function is
- 17.6 Suppose that, given
 , the random variable X is normally distributed with mean
, the random variable X is normally distributed with mean 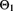 and variance
and variance  .
.
- Show that
 and
and  .
. - If
 and
and  are independent, show that X has the same distribution as
are independent, show that X has the same distribution as  , where
, where  and Y are independent and Y conditional on
and Y are independent and Y conditional on  is normally distributed with mean zero and variance
is normally distributed with mean zero and variance  .
.
- Show that
- 17.7 Suppose that
 has pdf
has pdf  , and
, and  has pdf
has pdf  . If, given
. If, given  , X is Poisson distributed with mean
, X is Poisson distributed with mean  , show that X has the same distribution as
, show that X has the same distribution as  , where Y and Z are independent, Y is Poisson distributed with mean
, where Y and Z are independent, Y is Poisson distributed with mean  , and
, and  is Poisson distributed with mean
is Poisson distributed with mean  .
. - 17.8 Consider a die–spinner model. The first die has one “marked” face and five “unmarked” faces, whereas the second die has four “marked” faces and two “unmarked” faces. There are three spinners, each with five equally spaced sectors marked 3 or 8. The first spinner has one sector marked 3 and four marked 8, the second has two marked 3 and three marked 8, and the third has four marked 3 and one marked 8. One die and one spinner are selected at random. If rolling the die produces an unmarked face, no claim occurs. If a marked face occurs, there is a claim and then the spinner is spun once to determine the amount of the claim.
- Determine
 for each of the six die–spinner combinations.
for each of the six die–spinner combinations. - Determine the conditional distributions
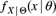 for the claim sizes for each die–spinner combination.
for the claim sizes for each die–spinner combination. - Determine the hypothetical means
 and the process variances
and the process variances  for each
for each  .
. - Determine the marginal probability that the claim
 on the first iteration equals 3.
on the first iteration equals 3. - Determine the posterior distribution
 of
of  using Bayes' theorem.
using Bayes' theorem. - Use (17.10) to determine the conditional distribution
 of the claims
of the claims  on the second iteration given that
on the second iteration given that  was observed on the first iteration.
was observed on the first iteration. - Use (17.13) to determine the Bayesian premium
 .
. - Determine the joint probability that
 and
and  for
for  , 3, 8.
, 3, 8. - Determine the conditional distribution
 directly using (17.8) and compare your answer to that of (f).
directly using (17.8) and compare your answer to that of (f). - Determine the Bayesian premium directly using (17.12) and compare your answer to that of (g).
- Determine the structural parameters
 , and a.
, and a. - Compute the Bühlmann credibility factor and the Bühlmann credibility premium to approximate the Bayesian premium
 .
.
- Determine
- 17.9 Three urns have balls marked 0, 1, and 2 in the proportions given in Table 17.3. An urn is selected at random, and two balls are drawn from that urn with replacement. A total of 2 on the two balls is observed. Two more balls are then drawn with replacement from the same urn, and it is of interest to predict the total on these next two balls.
- Determine
 .
. - Determine the conditional distributions
 for the totals on the two balls for each urn.
for the totals on the two balls for each urn. - Determine the hypothetical means
 and the process variances
and the process variances  for each
for each  .
. - Determine the marginal probability that the total
 on the first two balls equals 2.
on the first two balls equals 2. - Determine the posterior distribution
 using Bayes' theorem.
using Bayes' theorem. - Use (17.10) to determine the conditional distribution
 of the total
of the total  on the next two balls drawn, given that
on the next two balls drawn, given that  was observed on the first two draws.
was observed on the first two draws. - Use (17.13) to determine the Bayesian premium
 .
. - Determine the joint probability that the total
 on the next two balls equals
on the next two balls equals  and the total
and the total  on the first two balls equals 2 for
on the first two balls equals 2 for  .
. - Determine the conditional distribution
 directly using (17.8) and compare your answer to that of (f).
directly using (17.8) and compare your answer to that of (f). - Determine the Bayesian premium directly using (17.12) and compare your answer to that of (g).
- Determine the structural parameters
 , and a.
, and a. - Determine the Bühlmann credibility factor and the Bühlmann credibility premium.
- Show that the Bühlmann credibility factor is the same if each “exposure unit” consists of one draw from the urn rather than two draws.
Table 17.3 The data for Exercise 17.9.
Urn 0s 1s 2s 1 0.40 0.35 0.25 2 0.25 0.10 0.65 3 0.50 0.15 0.35 - Determine
- 17.10 Suppose that there are two types of policyholder: type A and type B. Two-thirds of the total number of the policyholders are of type A and one-third are of type B. For each type, the information on annual claim numbers and severity are given in Table 17.4. A policyholder has a total claim amount of 500 in the past four years. Determine the credibility factor Z and the credibility premium for next year for this policyholder.
Table 17.4 The data for Exercise 17.10.
Number of claims Severity Type Mean Variance Mean Variance A 0.2 0.2 200 4,000 B 0.7 0.3 100 1,500 - 17.11 Let
 represent the risk factor for claim numbers and let
represent the risk factor for claim numbers and let  represent the risk factor for the claim severity for a line of insurance. Suppose that
represent the risk factor for the claim severity for a line of insurance. Suppose that  and
and  are independent. Suppose also that, given
are independent. Suppose also that, given  , the claim number N is Poisson distributed and, given
, the claim number N is Poisson distributed and, given  , the severity Y is exponentially distributed. The expectations of the hypothetical means and process variances for the claim number and severity as well as the variance of the hypothetical means for frequency are, respectively,
, the severity Y is exponentially distributed. The expectations of the hypothetical means and process variances for the claim number and severity as well as the variance of the hypothetical means for frequency are, respectively,





Three observations are made on a particular policyholder and we observe total claims of 200. Determine the Bühlmann credibility factor and the Bühlmann premium for this policyholder.
- 17.12 Suppose that
 are independent (conditional on
are independent (conditional on  ) and that
) and that

Let

- Show that

and

- Solve the normal equations for
 to show that the credibility premium satisfies
to show that the credibility premium satisfies

where

- Show that
- 17.13 For the situation described in Exercise 13.5, determine
 and the Bayesian premium
and the Bayesian premium  . Why is the Bayesian premium equal to the credibility premium?
. Why is the Bayesian premium equal to the credibility premium? - 17.14 Suppose that, for
 ,
,

a negative binomial pf with
 a known quantity.
a known quantity.- Demonstrate that the conjugate prior from Theorem 13.18 is the beta pf

where
 and
and  are the acceptable parameter values for
are the acceptable parameter values for  to be a valid pdf.
to be a valid pdf. - Show that
 if
if  and
and  if
if  .
. - Show that there is no credibility premium if
 . Next, show that if
. Next, show that if  , then
, then  and
and  .
. - Prove that there is no Bayesian premium if the number of observations n satisfies
 and
and  , and that if
, and that if  , then the Bayesian premium is linear in the
, then the Bayesian premium is linear in the  . What happens if
. What happens if  ?
? - Show that credibility is exact if
 .
.
- Demonstrate that the conjugate prior from Theorem 13.18 is the beta pf
- 17.15 Consider the generalization of the linear exponential family given by

If m is a parameter, this is called the exponential dispersion family. In Exercise 5.25, it is shown that the mean of this random variable is
 . For this exercise, assume that m is known.
. For this exercise, assume that m is known.- Consider the prior distribution

Determine the Bayesian premium.
- Using the same prior, determine the Bühlmann premium.
- Show that the inverse Gaussian distribution is a member of the exponential dispersion family.
- Consider the prior distribution
- 17.16 Suppose that
 are independent (conditional on
are independent (conditional on  ) and
) and

Let
 ,
,  ,
,  ,
,  , and
, and  .
.- Discuss when these assumptions may be appropriate.
- Show that
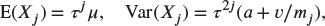
and
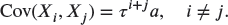
- Solve the normal equations for
 to show that the credibility premium satisfies
to show that the credibility premium satisfies
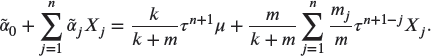
- Give a verbal interpretation of the formula in (c).
- Suppose that

Show that
 and that
and that  , where
, where 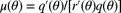 and
and  .
. - Determine the Bayesian premium if

- 17.17 Suppose that, given
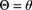 , the random variables
, the random variables  are independent with Poisson pf
are independent with Poisson pf
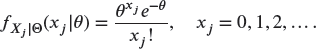
- Let
 . Show that S has pf
. Show that S has pf

where
 has pdf
has pdf  .
. - Show that the Bayesian premium is

- Evaluate the distribution of S in (a) when
 is a gamma distribution. What type of distribution is this?
is a gamma distribution. What type of distribution is this?
- Let
- 17.18 Suppose that, given
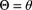 , the random variables
, the random variables  are independent with Poisson pf
are independent with Poisson pf

and
 has the inverse Gaussian pdf from Appendix A (with
has the inverse Gaussian pdf from Appendix A (with  replaced by
replaced by  ),
),
Define
 .
.- Use Exercise 5.20(g) to show that the posterior distribution of
 given that
given that  is the generalized inverse Gaussian distribution with pdf
is the generalized inverse Gaussian distribution with pdf

- Use part (a) and Exercise 5.20(g) to prove that the predictive distribution of
 given
given  is the Sichel distribution with pdf
is the Sichel distribution with pdf

for
 .
. - Use Example 7.16 to evaluate the pf

and, hence, use Exercise 17.17(b) to describe how to calculate the Bayesian premium.
- Use Exercise 5.20(g) to show that the posterior distribution of
- 17.19 Suppose that
 is normally distributed with mean
is normally distributed with mean  and variance v for
and variance v for  . Further suppose that
. Further suppose that  is normally distributed with mean
is normally distributed with mean  and variance a. Thus,
and variance a. Thus,

and

Determine the posterior distribution of
 and the predictive distribution of
and the predictive distribution of  . Then determine the Bayesian estimate of
. Then determine the Bayesian estimate of  . Finally, show that the Bayesian and Bühlmann estimates are equal.
. Finally, show that the Bayesian and Bühlmann estimates are equal. - 17.20 (*) Your friend selected at random one of two urns and then she pulled a ball with number 4 on it from the urn. Then she replaced the ball in the urn. One of the urns contains four balls, numbered 1–4. The other urn contains six balls, numbered 1–6. Your friend will make another random selection from the same urn.
- Estimate the expected value of the number on the next ball using the Bayesian method.
- Estimate the expected value of the number on the next ball using Bühlmann credibility.
- 17.21 The number of claims for a randomly selected insured has a Poisson distribution with parameter
 . The parameter
. The parameter  is distributed across the population with pdf
is distributed across the population with pdf 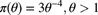 . For an individual, the parameter does not change over time. A particular insured experienced a total of 20 claims in the previous two years.
. For an individual, the parameter does not change over time. A particular insured experienced a total of 20 claims in the previous two years.
- (*) Determine the Bühlmann credibility estimate for the future expected claim frequency for this particular insured.
- Determine the Bayesian credibility estimate for the future expected claim frequency for this particular insured.
- 17.22 (*) The distribution of payments to an insured is constant over time. If the Bühlmann credibility assigned for one-half year of observation is 0.5, determine the Bühlmann credibility to be assigned for three years.
- 17.23 (*) Three urns contain balls marked either 0 or 1. In urn A, 10% are marked 0; in urn B, 60% are marked 0; and in urn C, 80% are marked 0. An urn is selected at random and three balls selected with replacement. The total of the values is 1. Three more balls are selected with replacement from the same urn.
- Determine the expected total of the three balls using Bayes' theorem.
- Determine the expected total of the three balls using Bühlmann credibility.
- 17.24 (*) The number of claims follows a Poisson distribution with parameter
 . A particular insured had three claims in the past three years.
. A particular insured had three claims in the past three years.
- The value of
 has pdf
has pdf  ,
, 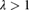 . Determine the value of K used in Bühlmann's credibility formula. Then use Bühlmann credibility to estimate the claim frequency for this insured.
. Determine the value of K used in Bühlmann's credibility formula. Then use Bühlmann credibility to estimate the claim frequency for this insured. - The value of
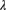 has pdf
has pdf  ,
,  . Determine the value of K used in Bühlmann's credibility formula. Then use Bühlmann credibility to estimate the claim frequency for this insured.
. Determine the value of K used in Bühlmann's credibility formula. Then use Bühlmann credibility to estimate the claim frequency for this insured.
- The value of
- 17.25 (*) The number of claims follows a Poisson distribution with parameter h. The value of h has the gamma distribution with pdf
 ,
,  . Determine the Bühlmann credibility to be assigned to a single observation. (The Bayes solution is obtained in Exercise 13.22.)
. Determine the Bühlmann credibility to be assigned to a single observation. (The Bayes solution is obtained in Exercise 13.22.) - 17.26 Consider the situation of Exercise 13.24.
- Determine the expected number of claims in the second year using Bayesian credibility.
- (*) Determine the expected number of claims in the second year using Bühlmann credibility.
- 17.27 (*) One spinner is selected at random from a group of three spinners. Each spinner is divided into six equally likely sectors. The number of sectors marked 0, 12, and 48, respectively, on each spinner is as follows: spinner A, 2,2,2; spinner B, 3,2,1; and spinner C, 4,1,1. A spinner is selected at random and a zero is obtained on the first spin.
- Determine the Bühlmann credibility estimate of the expected value of the second spin using the same spinner.
- Determine the Bayesian credibility estimate of the expected value of the second spin using the same spinner.
- 17.28 The number of claims in a year has a Poisson distribution with mean
 . The parameter
. The parameter  has the uniform distribution over the interval (1,3).
has the uniform distribution over the interval (1,3).
- (*) Determine the probability that a randomly selected individual will have no claims.
- (*) If an insured had one claim during the first year, estimate the expected number of claims for the second year using Bühlmann credibility.
- If an insured had one claim during the first year, estimate the expected number of claims for the second year using Bayesian credibility.
- 17.29 (*) Each of two classes, A and B, has the same number of risks. In class A, the number of claims per risk per year has mean
 and variance
and variance  , while the amount of a single claim has mean 4 and variance 20. In class B, the number of claims per risk per year has mean
, while the amount of a single claim has mean 4 and variance 20. In class B, the number of claims per risk per year has mean  and variance
and variance 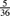 , while the amount of a single claim has mean 2 and variance 5. A risk is selected at random from one of the two classes and is observed for four years.
, while the amount of a single claim has mean 2 and variance 5. A risk is selected at random from one of the two classes and is observed for four years.
- Determine the value of Z for Bühlmann credibility for the observed pure premium.
- Suppose that the pure premium calculated from the four observations is 0.25. Determine the Bühlmann credibility estimate for the risk's pure premium.
- 17.30 (*) Let
 be the outcome of a single trial and let
be the outcome of a single trial and let  be the expected value of the outcome of a second trial. You are given the information in Table 17.5. Determine the Bayesian estimate for
be the expected value of the outcome of a second trial. You are given the information in Table 17.5. Determine the Bayesian estimate for  .
.
Table 17.5 The data for Exercise 17.30.
Outcome, T 
Bühlmann estimate of 
Bayesian estimate of 
1 1/3 2.72 2.6 8 1/3 7.71 7.8 12 1/3 10.57 – - 17.31 Consider the situation of Exercise 13.25.
- Determine the expected number of claims in the second year using Bayesian credibility.
- (*) Determine the expected number of claims in the second year using Bühlmann credibility.
- 17.32 Consider the situation of Exercise 13.26.
- Use Bayesian credibility to determine the expected number of claims in the second year.
- Use Bühlmann credibility to determine the expected number of claims in the second year.
- 17.33 Two spinners,
 and
and  , are used to determine the number of claims. For spinner
, are used to determine the number of claims. For spinner  , there is a 0.15 probability of one claim and 0.85 of no claim. For spinner
, there is a 0.15 probability of one claim and 0.85 of no claim. For spinner  , there is a 0.05 probability of one claim and 0.95 of no claim. If there is a claim, one of two spinners,
, there is a 0.05 probability of one claim and 0.95 of no claim. If there is a claim, one of two spinners,  and
and  , is used to determine the amount. Spinner
, is used to determine the amount. Spinner  produces a claim of 20 with probability 0.8 and 40 with probability 0.2. Spinner
produces a claim of 20 with probability 0.8 and 40 with probability 0.2. Spinner  produces a claim of 20 with probability 0.3 and 40 with probability 0.7. A spinner is selected at random from each of
produces a claim of 20 with probability 0.3 and 40 with probability 0.7. A spinner is selected at random from each of  and from
and from  . Three observations from the selected pair yield claim amounts of 0, 20, and 0.
. Three observations from the selected pair yield claim amounts of 0, 20, and 0.
- (*) Use Bühlmann credibility to separately estimate the expected number of claims and the expected severity. Use these estimates to estimate the expected value of the next observation from the same pair of spinners.
- Use Bühlmann credibility once on the three observations to estimate the expected value of the next observation from the same pair of spinners.
- (*) Repeat parts (a) and (b) using Bayesian estimation.
- (*) For the same selected pair of spinners, determine

- 17.34 (*) A portfolio of risks is such that all risks are normally distributed. Those of type A have a mean of 0.1 and a standard deviation of 0.03. Those of type B have a mean of 0.5 and a standard deviation of 0.05. Those of type C have a mean of 0.9 and a standard deviation of 0.01. There are an equal number of each type of risk. The observed value for a single risk is 0.12. Determine the Bayesian estimate of the same risk's expected value.
- 17.35 (*) You are given the following:
- The conditional distribution
 is a member of the linear exponential family.
is a member of the linear exponential family. - The prior distribution
 is a conjugate prior for
is a conjugate prior for  .
.  .
. , where
, where 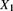 is the value of a single observation.
is the value of a single observation.- The expected value of the process variance
 .
.
Determine the variance of the hypothetical means
 .
. - The conditional distribution
- 17.36 (*) You are given the following:
- X is a random variable with mean
 and variance v.
and variance v.  is a random variable with mean 2 and variance 4.
is a random variable with mean 2 and variance 4.- v is a random variable with mean 8 and variance 32.
Determine the value of the Bühlmann credibility factor Z after three observations of X.
- X is a random variable with mean
- 17.37 The amount of an individual claim has an exponential distribution with pdf
 . The parameter
. The parameter  has an inverse gamma distribution with pdf
has an inverse gamma distribution with pdf  .
.
- (*) Determine the unconditional expected value,
 .
. - Suppose that two claims were observed with values 15 and 25. Determine the Bühlmann credibility estimate of the expected value of the next claim from the same insured.
- Repeat part (b), but determine the Bayesian credibility estimate.
- (*) Determine the unconditional expected value,
- 17.38 The distribution of the number of claims is binomial with
 and
and  unknown. The parameter
unknown. The parameter  is distributed with mean 0.25 and variance 0.07. Determine the value of Z for a single observation using Bühlmann's credibility formula.
is distributed with mean 0.25 and variance 0.07. Determine the value of Z for a single observation using Bühlmann's credibility formula. - 17.39 (*) Consider four marksmen. Each is firing at a target that is 100 feet away. The four targets are 2 feet apart (i.e. they lie on a straight line at positions 0, 2, 4, and 6 in feet). The marksmen miss to the left or right, never high or low. Each marksman's shot follows a normal distribution with mean at his target and a standard deviation that is a constant times the distance to the target. At 100 feet, the standard deviation is 3 feet. By observing where an unknown marksman's shot hits the straight line, you are to estimate the location of the next shot by the same marksman.
- Determine the Bühlmann credibility assigned to a single shot of a randomly selected marksman.
- Which of the following will increase Bühlmann credibility the most?
- Revise the targets to 0, 4, 8, and 12.
- Move the marksmen to 60 feet from the targets.
- Revise the targets to 2, 2, 10, and 10.
- Increase the number of observations from the same marksman to three.
- Move two of the marksmen to 50 feet from the targets and increase the number of observations from the same marksman to two.
- 17.40 (*) Risk 1 produces claims of amounts 100, 1,000, and 20,000 with probabilities 0.5, 0.3, and 0.2, respectively. For risk 2, the probabilities are 0.7, 0.2, and 0.1. Risk 1 is twice as likely as risk 2 of being observed. A claim of 100 is observed, but the observed risk is unknown.
- Determine the Bayesian credibility estimate of the expected value of the second claim amount from the same risk.
- Determine the Bühlmann credibility estimate of the expected value of the second claim amount from the same risk.
- 17.41 (*) You are given the following:
- The number of claims for a single insured follows a Poisson distribution with mean M.
- The amount of a single claim has an exponential distribution with pdf

- M and
 are independent.
are independent.  and
and  .
. and
and  .
.- The number of claims and the claim amounts are independent.
- Determine the expected value of the pure premium's process variance for a single risk.
- Determine the variance of the hypothetical means for the pure premium.
- 17.42 (*) The number of claims has a Poisson distribution. For 75% of risks,
 , and for 25% of risks,
, and for 25% of risks,  . A randomly selected risk had r claims in year 1. The Bayesian estimate of the expected number of claims in year 2 is 2.98. Determine the Bühlmann estimate of the expected number of claims in year 2.
. A randomly selected risk had r claims in year 1. The Bayesian estimate of the expected number of claims in year 2 is 2.98. Determine the Bühlmann estimate of the expected number of claims in year 2. - 17.43 (*) Claim sizes have an exponential distribution with mean
 . For 80% of risks,
. For 80% of risks,  , and for 20% of risks,
, and for 20% of risks,  . A randomly selected policy had a claim of size 5 in year 1. Determine both the Bayesian and Bühlmann estimates of the expected claim size in year 2.
. A randomly selected policy had a claim of size 5 in year 1. Determine both the Bayesian and Bühlmann estimates of the expected claim size in year 2. - 17.44 (*) A portfolio has 100 risks with identical and independent numbers of claims. The number of claims for one risk has a Poisson distribution with mean
 . The prior distribution is
. The prior distribution is  ,
,  . During year 1, 90 risks had 0 claims, 7 had 1 claim, 2 had 2 claims, and 1 had 3 claims. Determine both the Bayesian and Bühlmann estimates of the expected number of claims for the portfolio in year 2.
. During year 1, 90 risks had 0 claims, 7 had 1 claim, 2 had 2 claims, and 1 had 3 claims. Determine both the Bayesian and Bühlmann estimates of the expected number of claims for the portfolio in year 2. - 17.45 (*) For a portfolio of risks, all members' aggregate losses per year per exposure have a normal distribution with a standard deviation of 1,000. For these risks, 60% have a mean of 2,000, 30% have a mean of 3,000, and 10% have a mean of 4,000. A randomly selected risk had the following experience over three years. In year 1, there were 24 exposures with total losses of 24,000. In year 2, there were 30 exposures with total losses of 36,000. In year 3, there were 26 exposures with total losses of 28,000. Determine the Bühlmann–Straub estimate of the mean aggregate loss per year per exposure for year 4.
- 17.46 (*) The number of claims for each policyholder has a binomial distribution with
 and q unknown. The prior distribution of q is beta with parameters a unknown,
and q unknown. The prior distribution of q is beta with parameters a unknown,  , and
, and  . A randomly selected policyholder had two claims in year 1 and k claims in year 2. Based on the year 1 experience, the Bayesian estimate of the expected number of claims in year 2 is 2.54545. Based on years 1 and 2, the Bayesian estimate of the expected number of claims in year 3 is 3.73333. Determine k.
. A randomly selected policyholder had two claims in year 1 and k claims in year 2. Based on the year 1 experience, the Bayesian estimate of the expected number of claims in year 2 is 2.54545. Based on years 1 and 2, the Bayesian estimate of the expected number of claims in year 3 is 3.73333. Determine k. - 17.47 In Example 17.13, if
 , then
, then 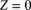 , and the estimator is
, and the estimator is  . That is, the data should be ignored. However, as
. That is, the data should be ignored. However, as  increases toward 1, Z increases to 1, and the sample mean becomes the preferred predictor of
increases toward 1, Z increases to 1, and the sample mean becomes the preferred predictor of 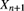 . Explain why this is a reasonable result.
. Explain why this is a reasonable result. - 17.48 In the following, let the random vector X represent all the past data and let
 represent the next observation. Let
represent the next observation. Let 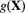 be any function of the past data.
be any function of the past data.
- Prove that the following is true:

where the expectation is taken over
 .
. - Show that setting
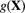 equal to the Bayesian premium (the mean of the predictive distribution) minimizes the expected squared error,
equal to the Bayesian premium (the mean of the predictive distribution) minimizes the expected squared error,

- Show that, if
 is restricted to be a linear function of the past data, then the expected squared error is minimized by the credibility premium.
is restricted to be a linear function of the past data, then the expected squared error is minimized by the credibility premium.
- Prove that the following is true:


















