13.3 Global Transfer of Control with Continuations

Armed with an elementary understanding of the concept of a continuation and how to capture a continuation in Scheme, we present some practical examples of first-class continuations. While continuations are used for a variety of purposes in these examples, all of these examples use call/cc for global transfer of control.

13.3.1 Nonlocal Exits

A common application of a first-class continuation is to program abnormal flows of control, such as a nonlocal exit from recursion without having to return through multiple layers of recursion. Consider the following recursive definition of a Scheme function product that accepts a list of numbers and returns the product of the numbers:

This function exhibits recursive control behavior, meaning that when the function is called its execution causes the stack to grow until the base case of the recursion is reached. At that point, the computation is performed as recursive calls return and pop off the stack. The following series of expressions depicts this process:

Rotating this series of expansions 90 degrees to the left yields a parabola-shaped curve. The x-axis of that parabola can be interpreted as time, while the y-axis represents memory. As time proceeds, the function requires an ever-increasing amount of memory. Once it hits the maximum point at the base case, it starts to occupy less and less memory until it finally terminates. This is the manner in which most recursive functions operate. This process remains unchanged irrespective of the input list passed to product. For instance, consider another invocation of the function with a list of numbers that includes a zero:

As soon as a zero is encountered in the list, the final return value of the function is known to be zero. However, the recursive control behavior continues to build up the stack of pending computations until the base case is reached, which signals the commencement of the computations to be performed. This function is inefficient in space whether the input contains a zero or not. It is inefficient in time only when the input list contains a zero—unnecessary multiplications are performed.

The presence of a zero in the input list can be considered an exception or exceptional case. Exceptions are unusual situations that happen at run-time, such as erroneous input. One application of first-class continuations is for exception handling.

We want to break out of the recursion as soon as we encounter a zero in the input list of numbers. Consider the following new definition of product (Dybvig 2003):

If product is invoked as 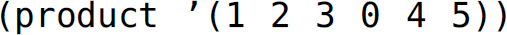, the continuation bound to break on line 5 is (lambda (returnvalue) returnvalue), which is the identity function, because there are no pending computations waiting for product to complete. If product is invoked as 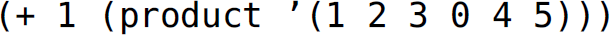, the continuation bound to break on line 5 is (lambda (returnvalue) (+ 1 returnvalue)). When passed a list of numbers including a zero, product aborts the current continuation (i.e., the pending computations built up on the stack) and uses the continuation of the first call to product to break out to the main read-eval-print loop (line 11). This action is called a nonlocal exit because the local exit to this function is through the termination of the recursion as the stack naturally unwinds. The function builds up the capability of calling a series of multiplication operators, but does so only after the function has determined that the input list does not contain a zero. The function goes through the list in a left-to-right order, building up these multiplication computations. Once the function has determined that the input list does not contain a zero, the multiplication operations are conducted in a right-to-left fashion as the function backs out of the recursion:

The case where the list does not contain a zero proceeds as usual, using the current continuation of pending multiplications on the stack rather than the captured continuation of the initial call to product. Like the examples in Section 13.2, this product function demonstrates that once a continuation is captured through call/cc, a programmer can use (i.e., call) the captured continuation to replace the current continuation elsewhere in a program, when desired, to circumvent the normal flow of control and, therefore, alter control flow.

Notice that in this example, the definition of the nested function P within the letrec expression (lines 6–13) is necessary because we want to capture the continuation of the first call to product, rather than recapturing a continuation every time product is called recursively. For instance, the following definition of product does not achieve the desired effect because the continuation break is rebound on each recursive call and, therefore, is not the exceptional/abnormal continuation, but rather the normal continuation of the computation:

We continue with 5 (line 11) to demonstrate that the continuation stored in break is actually the normal continuation:

To break out of this type letrec-free style of function definition, the function could be defined to accept an abnormal continuation, but the caller would be responsible for capturing and passing it to the called function. For instance:

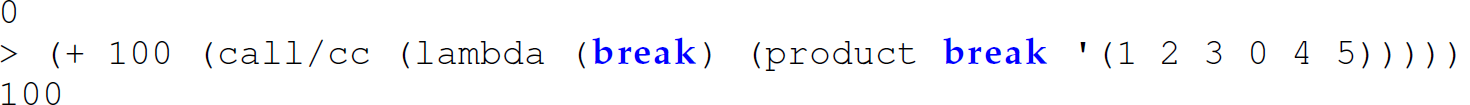
Factoring out the constant parameter break (using Functional Programming Design Guideline 6 from Table 5.7 in Chapter 5) again renders a definition of product using letrec expression:

While first-class continuations are used in these examples for programming efficient nonlocal exits, continuations have a broader context of applications, as we demonstrate in this chapter.

13.3.2 Breakpoints

Consider the following recursive definition of a Scheme factorial function that accepts an integer n and returns the factorial of n:

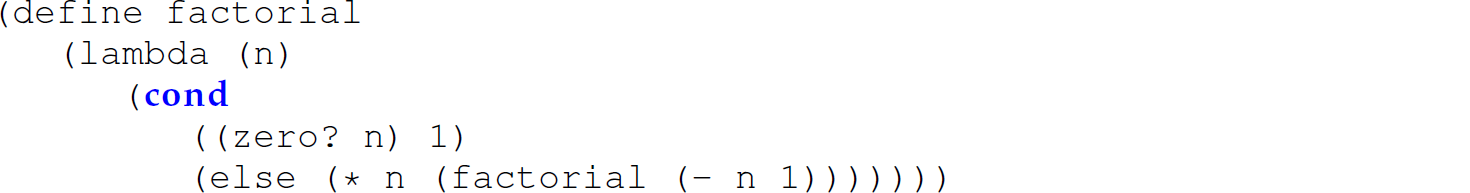
Now consider the same definition of factorial using call/cc to capture the continuation of the base case (i.e., where n is 0) (Dybvig 2009, pp. 75–76):

Unlike the continuation captured in the product example in Section 13.3.1, where the continuation captured is of the initial call to the recursive function product (i.e., the identity function), here the continuation captured includes all of the pending multiplications built up on the stack when the base of the recursion (i.e., n = 0) is reached. For instance, when n = 5, the continuation captured and bound to k is

Moreover, unlike in the product example, here the captured continuation is not invoked from the lambda expression passed to call/cc. Instead, the continuation is stored in the variable redo using the assignment operator set!. The consequence of this side effect is that the captured continuation can be invoked from the main read-eval-print loop after factorial terminates, when and as many times as desired. In other words, the continuation captured by call/cc is invoked after the function passed to call/cc returns:

The natural base case of recursion for factorial is 1. However, by invoking the continuation captured through the use of call/cc, we can dynamically change the base case of the recursion at run-time. Moreover, this factorial example vividly demonstrates the—perhaps mystifying—unlimited extent of a first-class continuation.

The thought of transferring control to pending computations that no longer exist on the run-time stack hearkens back the examples of first-class closures returned from functions (in Chapter 6) that “remembered” their lexical environment even though that environment no longer existed because the activation record for the function that created and returned the closure had been popped off the stack (Section 6.10).

The continuation captured by call/cc is, more generally, a closure—a pair of (code, environment) pointers—where the code is the actual continuation and the environment is the environment in which the code is to be later evaluated. However, when invoked, the continuation (in the closure) captured with call/cc, unlike a regular closure (i.e., one whose code component is not a continuation), does not return a value, but rather transfers control elsewhere. Similarly, when we invoke redo, we are jumping back to activation records (i.e., stack frames) that no longer exist on the stack because the factorial function has long since terminated, and been popped off the stack, by the time redo is called. The key connection back to our discussion of first-class closures in Chapter 6 is that the first-class continuations captured through call/cc are only possible because closures in Scheme are allocated from the heap and, therefore, have unlimited extent. If closures in Scheme were allocated from the run-time stack, an example such as factorial, which uses a first-class continuation to jump back to seemingly “phantom” stack frames, would not be possible.

The factorial example illustrates the use of first-class continuations for breakpoints and can be used as a basis for a breakpoint facility in a debugger. In particular, the continuation of the breakpoint can be saved so that the computation may be restarted from the breakpoint—more than once, if desired, and, with different values.

Unlike in the prior examples, here we store the captured continuation in a variable through assignment, using the set! operator. This demonstrates the first-class status of continuations in Scheme. Once a continuation is captured through call/cc, a programmer can store the continuation in a variable (or data structure) for later use. The programmer can then use the captured continuation to replace the current continuation elsewhere in a program, when and as many times as desired (now that it is recorded persistently in a variable), to circumvent the normal flow of control and, therefore, manipulate control flow. There is no limit on the number of times a continuation can be called, which implies that heap-allocated activation records must exist.

13.3.3 First-Class Continuations in Ruby

In an expression-oriented language, the continuation of an expression is the calling expression, which is generally found to the left or above the expression whose continuation is being captured (as in our invocations of call/cc). In a language whose control flows along a sequential execution of statements, the continuation of a statement is the set of statements following the statement whose continuation is being captured. Consider the following product function in Ruby—a language whose statements are executed sequentially:

Ruby does not support nested methods. Thus, instead of capturing the continuation of a local, nested function P (as done in the second definition of product in Section 13.3.1), here the caller saves the captured continuation k with callcc³ of each called function (lines 22–23 and 28–29) in a global variable $break (lines 22 and 28) so that the called function has access to it. The continuation captured in the local variable k on line 22 represents the set of program statements on lines 24–31. Similarly, the continuation captured in the local variable k on line 28 represents the set of program statements on lines 30–31. In each case, the captured continuation in the local variable k is saved persistently in the global variable $break so that it can be accessed in the definition of product by using $break and called by using $break.call with the string argument "Encountered a zero. Break out." (line 9). The output of this program is

Lines 2–10 of the output demonstrate that the product of a list of non-zero numbers is computed while popping out of the (four) layers of recursive calls. Lines 11– 13 of the output demonstrate that no multiplications are performed when a zero is encountered in the input list of numbers (i.e., the nonlocal exit abandons the recursive calls on the stack).

Conceptual Exercises for Section 13.3

Exercise 13.3.1 Does the following definition of product perform any unnecessary multiplications? If so, explain how and why (with reasons). If not, explain why not (with reasons).

Exercise 13.3.2 Can the factorial function using call/cc given in this section be redefined to remove the side effect (i.e., without use set!), yet retain the ability to dynamically alter the base of the recursion? If so, define it. If not, explain why not. In other words, why is side effect necessary in that example (if it is)?

Exercise 13.3.3 Explain why the letrec expression is necessary in the definition of product using call/cc in this section. In other words, why can’t product be defined just as effectively as follows? Explain.

Exercise 13.3.4 Consider the following attempt to remove the side effect (i.e., the use of set!) from the factorial function using call/cc given in this section:

The approach taken is to have factorial return a pair whose car is an integer representing the factorial of its argument and whose cdr is the redo continuation, rather than just an integer representing the factorial. As can be seen from the preceding transcript, this approach does not work.

(a) Notice that (cdr (factorial 5)) returns the continuation of the base case (i.e., the redo continuation). Explain why that rather than passing a single number to it, as done in the example in this section, now a pair must be passed instead—for example, the list (cons 2 "ignore") in this case.

(b) Evaluating 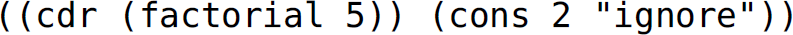results in an error. Explain why. You may want to try using the tracing (step-through) ability provided through the Racket debugging facility to help construct a clearer picture of the internal process.

(c) Explain why the invocation to factorial and subsequent use of the continuation as never terminates.

Exercise 13.3.5 Consider the following definition of product:

(a) Indicate how many (i.e., the number of) continuations are captured when this function is called as (product ’(9 12 7 3)).

(b) Indicate how many (i.e., the number of) continuations are captured when this function is called as (product ’(42 11 0 2 -1)).

Programming Exercises for Section 13.3

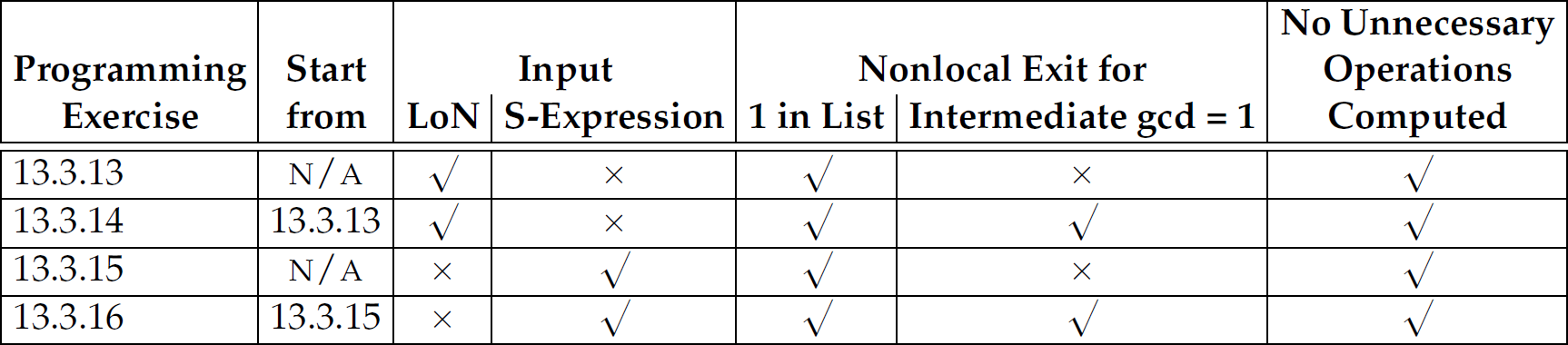
Table 13.1 presents a mapping from the greatest common divisor exercises here to some of the essential aspects of first-class continuations and call/cc.

Table 13.1 Mapping from the Greatest Common Divisor Exercises in This Section to the Essential Aspects of First-Class Continuations and call/cc

Exercise 13.3.6 Define a recursive Scheme function member1 that accepts only an atom a and a list of atoms lat and returns the integer position of a in lat (using zero-based indexing) if a is a member of lat and #f otherwise. Your definition of member1 must use call/cc to avoid returning back through all the recursive calls when the element a is not found in the list, but it must not use the captured continuation when the element a is found in the list.

Examples:

Exercise 13.3.7 Complete Programming Exercise 13.3.6 in Ruby using callcc.

Exercise 13.3.8 Define a Scheme function map-reciprocal, which uses map, that accepts only a list of numbers lon and returns a list containing the reciprocal of each number in lon. Use call/cc to foster an immediate nonlocal exit of the function as soon as a 0 is encountered in lon without returning through each of the recursive calls on the stack.

Exercise 13.3.9 Complete Programming Exercise 13.3.8 in Ruby using callcc.

Exercise 13.3.10 Rewrite the Ruby program in Section 13.3.3 so that the caller passes the captured continuation k of the called function product on lines 23 and 29 to the called function itself (as done in the third definition of product in Section 13.3.1).

Exercise 13.3.11 Define a Scheme function product that accepts a variable number of arguments and returns the product of them. Define product using call/cc such that no multiplications are performed if any of the arguments are zero.

Exercise 13.3.12 (Friedman, Wand, and Haynes 2001, Exercise 1.17.1, p. 27) Consider the following BNF specification of a binary search tree.

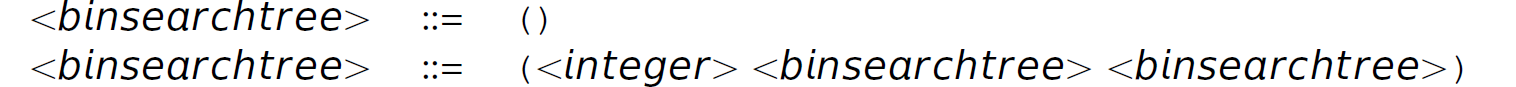
Define a Scheme function path that accepts only an integer n and a list bst representing a binary search tree, in that order, and returns a list of lefts and rights indicating how to locate the vertex containing n. If the integer is not found in the binary search tree, use call/cc to avoid returning back through all the recursive calls and return the atom ’notfound.

Examples:

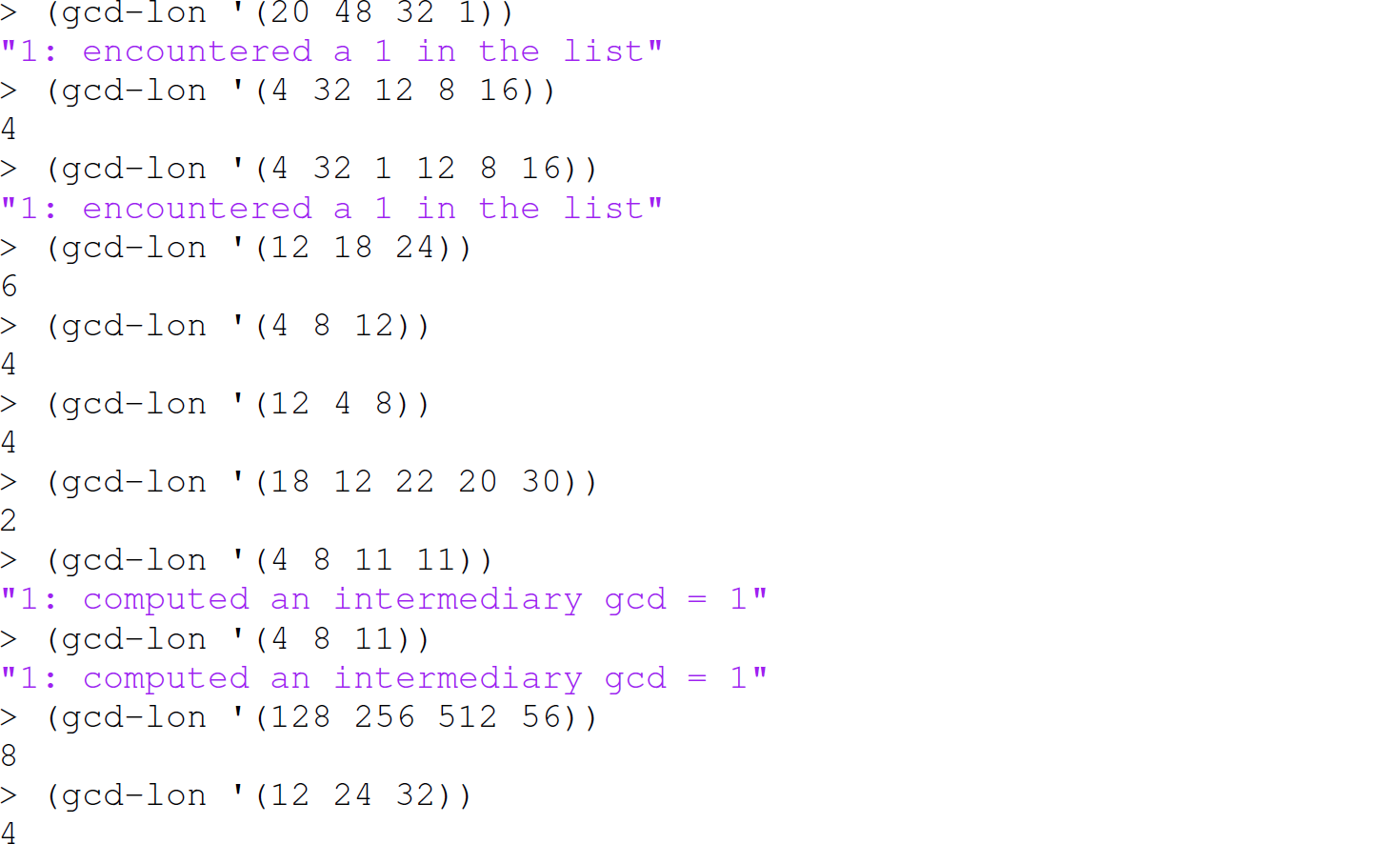
Exercise 13.3.13 Define a function gcd-lon in Scheme using call/cc that accepts only a non-empty list of positive, non-zero integers and returns the greatest common divisor of those integers. If a 1 is encountered in the list, through the use of call/cc, return the string "1: encountered a 1 in the list" immediately without ever executing gcd (which is defined in Racket Scheme) and without returning through each of the recursive calls on the stack.

Examples:

Exercise 13.3.14 Modify the solution to Programming Exercise 13.3.13 so that if a 1 is ever computed as the result of an intermediate call to gcd, through the use of call/cc, the string "1: computed an intermediary gcd = 1" is returned immediately without returning through each of the recursive calls on the stack and before performing any additional arithmetic computations.

Examples:

Exercise 13.3.15 Define a function gcd* in Scheme using call/cc that accepts only a non-empty S-expression of positive, non-zero integers, which contains no empty lists, and returns the greatest common divisor of those integers. If a 1 is encountered in the list, through the use of call/cc, return the string "1: encountered a 1 in the S-expression" immediately without ever executing gcd and without returning through each of the recursive calls on the stack.

Examples:

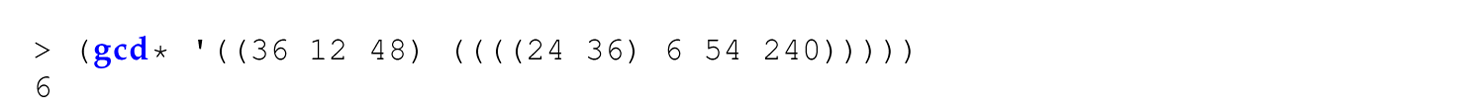
Exercise 13.3.16 Modify the solution to Programming Exercise 13.3.15 so that if a 1 is ever computed as the result of an intermediate call to gcd, through the use of call/cc, the string "1: computed an intermediary gcd = 1" is returned immediately without returning through each of the recursive calls on the stack and before performing any additional arithmetic computations.

Examples:

Exercise 13.3.17 Define a function intersect* in Scheme using call/cc that accepts only a list of lists as an argument and returns the set intersection of these lists. Your function must not perform any unnecessary computations. Specifically, if the input list contains an empty list, immediately return () without returning through each of the recursive calls on the stack. Further, if the input list does not contain an empty list, but contains two lists whose set intersection is empty, immediately return (). You may assume that each list in the input list represents a set (i.e., contains no duplicate elements). Your solution must follow Design Guidelines 4 and 6 from Table 5.7 in Chapter 5.

3. While the examples in Ruby in this chapter run in the current version of Ruby, callcc is currently deprecated in Ruby.