14.4 Resolution

14.4.1 Resolution in Propositional Calculus

There are multiple rules of inference in formal systems of logic that are used to infer new propositions from given propositions. For instance, modus ponens is a rule of inference: (p ∧ (p ⊃ q)) ⊃ q (if p implies q, and p, therefore q), often written 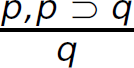. Application of modus ponens supports the elimination of antecedents (e.g., p) from a logical proof and, therefore, is referred to as the rule of detachment. Resolution is the primary rule of inference used in logic programming. Resolution is designed to be used with propositions in CNF. It can be stated as follows:

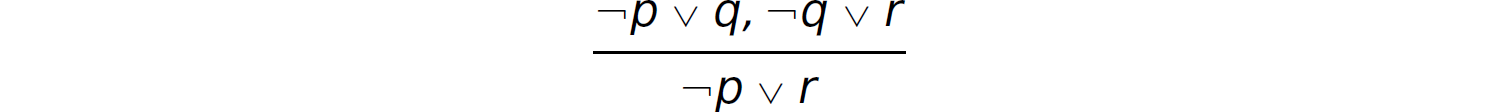
This rule indicates that if ¬ p ∨ q and ¬ q ∨ r areassumedto betrue, then ¬ p ∨ r is true. According to the rule of resolution, given two propositions (e.g., ¬ p ∨ q and q ∨ r) where the same term (e.g., q) is present in one and negated in another, a new proposition is deduced by uniting the two original propositions without the matched term (e.g., ¬p ∨ r). The underlying intuition being that the proposition q does not contribute to the validity of ¬ p ∨ r. The main idea in the application of resolution is to find two propositions in CNF such that the negation of a term in one is present in the other. When two such propositions are found, they can be combined with a disjunction after canceling out the matched terms in both:

Thus, given the propositions ¬ p ∨ q and ¬ q ∨ r, we can infer ¬ p ∨ r.

14.4.2 Resolution in Predicate Calculus

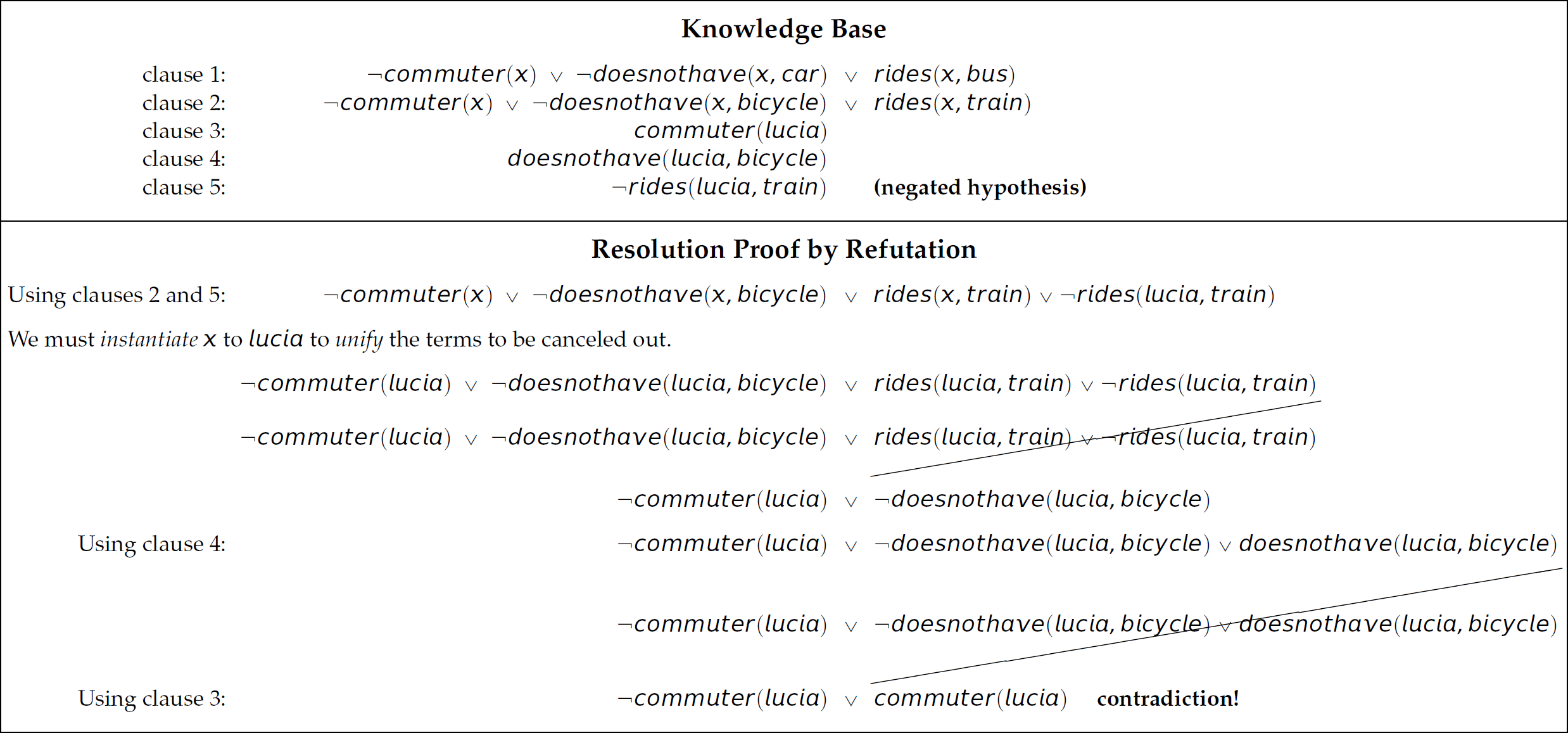
Resolution in propositional calculus similarly involves matching a proposition with its negation: p and ¬ p. Resolution in predicate calculus is not as simple because the arguments of the predicates must be considered. The structure of the following resolution proof is the same as in the prior example, except that the propositions p, q, and r are represented as binary predicates:

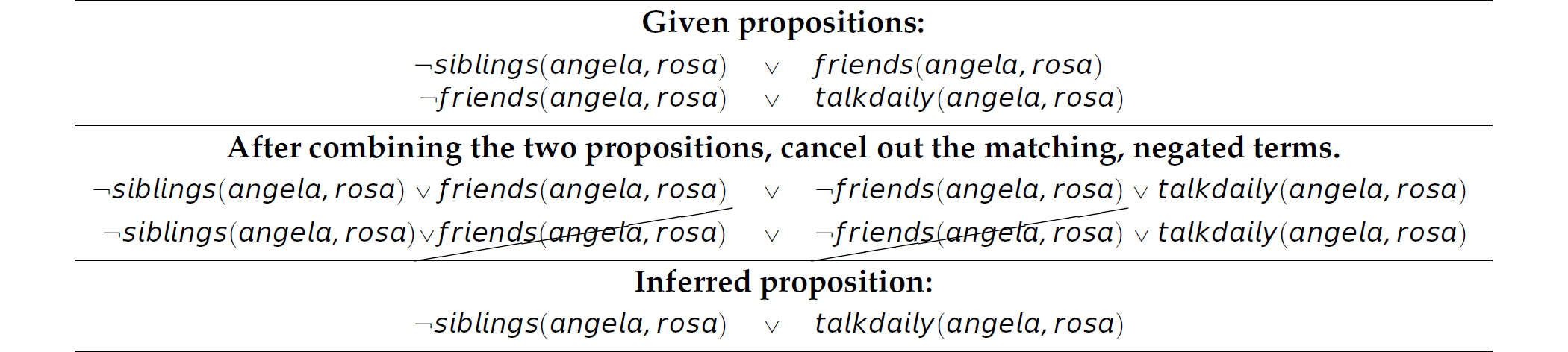
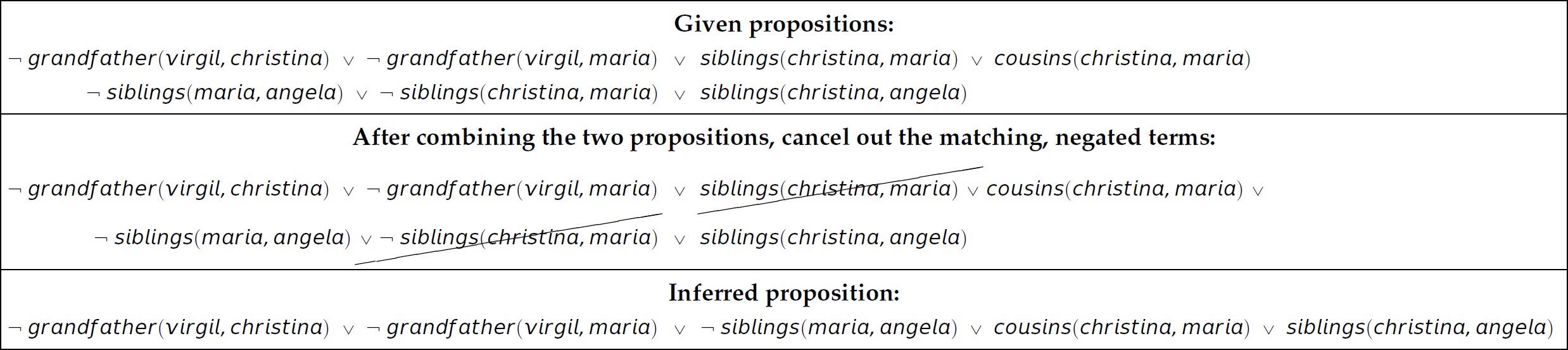
At present, we are not concerned with any intended semantics of any propositions, but are simply exploring the mechanics of resolution. Consider the example of an application of resolution in Table 14.6.

Table 14.6 An Example Application of Resolution

In the prior examples, the process of resolution started with the axioms (i.e., the propositions assumed to be true), from which was produced a new, inferred proposition. This approach to the application of resolution is called forward chaining. The question being asked is: What new propositions can we derive from the existing propositions? An alternative use of resolution is to test a hypothesis represented as a proposition for validity. We start by adding the negation of the hypothesis to the set of axioms and then run resolution. The process or resolution continues as usual until a contradiction is found, which indicates that the hypothesis is proved to be true (i.e., it is a theorem). This process produces a proof by refutation. Consider a knowledge base of one axiom commuter(lucia) and the hypothesis commuter(lucia). We add commuter(lucia) to the knowledge base and run resolution:

Thus, the hypothesis commuter(lucia) is true.

The presence of variables in propositions represented as predicates makes matching propositions during the process of resolution considerably more complex than the process demonstrated in the preceding examples. The process of “matching propositions” is formally called unification. Unification is the activity of finding a substitution or mapping that, when applied, renders two terms equivalent. The substitution is said to unify the two terms. Unification in the presence of variables requires instantiation—the temporary binding values to variables. The instantiation is temporary because the unification process often involves backtracking. Instantiation is the process of finding values for variables that will foster unification; it recurs throughout the process of unification. Consider the example of a resolution proof by refutation involving variables in Table 14.7, where the hypothesis to be proved is ridesplucia, trainq. Since a contradiction is found, the hypothesis rides(lucia, train) is proved to be true.

Table 14.7 An Example of a Resolution Proof by Refutation, Where the Propositions Therein Are Represented in CNF