2.3 Regular Expressions and Regular Languages
2.3.1 Regular Expressions
Since languages can be infinite, we need a concise, yet formal method of describing languages. A regular expression is a pattern represented as a string that concisely and formally denotes the strings of a language. A regular expression is itself a string in a language, albeit a metalanguage—a language used to describe a language. Thus, regular expressions have their own alphabet and syntax, not to be confused with the alphabet and syntax of the language that a regular expression is used to define.
Table 2.3 presents the six primitive constructs from which any regular expression can be constructed. These constructs are factored into three primitive regular expressions (i.e.,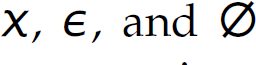 
) and three compound regular expressions (constructed with the*, concatenation, and + operators). Thus, some characters in the alphabet of regular expressions are special and called metacharacters [e.g., 
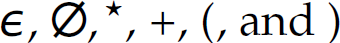].1 In particular, 
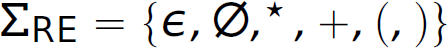. We have already encountered the * (or Kleene closure) operator as applied to a set of symbols (or alphabet). Here, it is applied to a regular expression r, where r* denotes zero or more occurrences of r. For instance, the regular expression opus* defines the language 
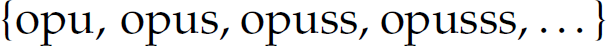. The regular expression (ab)* denotes the language 
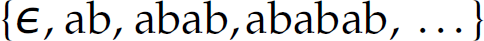. In both cases, the set of sentences, and therefore the language, are infinite. In short, a regular expression denotes a set of strings (i.e., the sentences of the language that the regular expression denotes).
Table 2.3 Regular Expressions (Key: χ ∈ Σ.)
Regular Expression | Denotes | Language |
|---|---|---|
|
Atomic Regular Expressions | ||
|
χ ε ∅ |
the single character χ empty string empty set |
L (χ) = χ L (∈) = ∈ L (∅) = {} |
|
Compound Regular Expressions | ||
|
(r*) (r1r2) (r1 + r2) |
zero or more of r1 concatenation of r1 and r2 either r1 or r2 |
L((r)*) = L(r)* L(r1r2) = L(r1)L(r2) L(r1 + r2) = L(r1) ∪ L(r2) |
The + operator is used to construct a compound regular expression from two subexpressions, where the language denoted by the compound expression contains the strings from the union of the sets denoted by the two subexpressions. For instance, the regular expression 
denotes 
. Similarly,
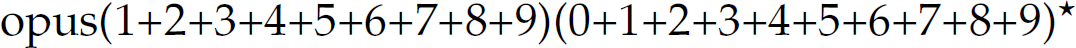
denotes the language
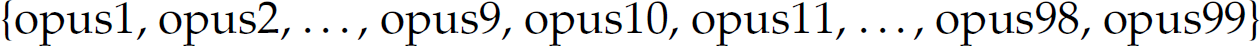
and
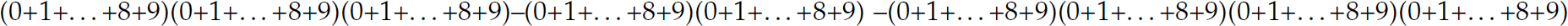
which denotes the language of Social Security numbers.
Table 2.4 presents a set of compound regular expressions with the associated language that each denotes. Parentheses in compound regular expressions are used for grouping subexpressions. In the absence of parentheses, highest to lowest precedence proceeds in a top-down manner, as shown in Table 2.3 (e.g., * has the highest precedence and + has the lowest precedence).
Table 2.4 Examples of Regular Expression (Σre = {∈, ∅, *, +, (,)}.)
Regular Expression | Denotes | Regular Language |
|---|---|---|
|
abc a + b + c a + e + i + o + u ∈ + a a(b + c) ab + cd a(b + c)d a* aa* aaaa* aaaaaaaa a + aa + aaa + aaaa + aaaaa aaa + aaaa + aaaaa + aaaaaa |
the string abc any one character in the set {a, b, c} any one character in the set {a, e, i, o, u} “a” or the empty string “a” followed by any character in the set {b, c} any one string in the set {ab, cd} “a” followed by any character in the set {b, c} followed by “d” “a” zero or more times “a” one or more times “a” three or more times “a” exactly eight times “a” between one and five times “a” between three and six times |
{abc} {a, b, c} {a, e, i, o, u} {∈, a} {ab, ac} {ab, cd} {abd, acd} {∈, a, aa, aaa, . . . } {a, aa, aaa, . . . } {aaa, aaaa, aaaaa, . . . } {aaaaaaaa} {a, aa, aaa, aaaa, aaaaa} {aaa, aaaa, aaaaa, aaaaaa} |
An enumeration of the elements of a set of sentences defines a formal language extensionally, while a regular expression defines a formal language intensionally.
A regular expression is a denotational construct for a (certain type of) formal language. In other words, a regular expression denotes sentences from the language it represents. For example, the regular expression opus* denotes the language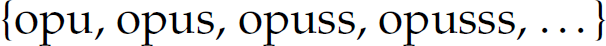 
.
Regular expressions are implemented in a variety of UNIX tools (e.g., 
). Most programming languages implement regular expressions either natively in the case of scripting languages (e.g., Perl and Tcl) or through a library or package (e.g., Python, Java, Go).2
2.3.2 Finite-State Automata
Recall that a regular expression intensionally denotes (the sentences of) a regular language. Now we turn to a computational mechanism that can decide whether a string is a sentence in a particular language—the set-membership problem mentioned previously. A finite-state automaton (FSA) isa model of computation used to recognize whether a string is a sentence in a particular language. Figure 2.1 presents a finite-state automaton3 that recognizes sentences in the language denoted by the regular expression
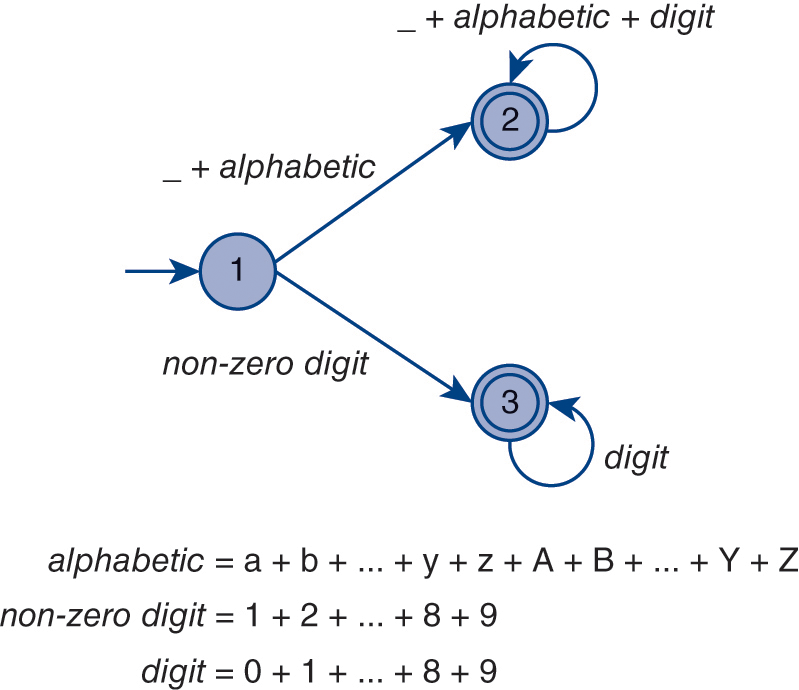
Figure 2.1 A finite-state automaton for a legal identifier and positive integer in the C programming language.
Description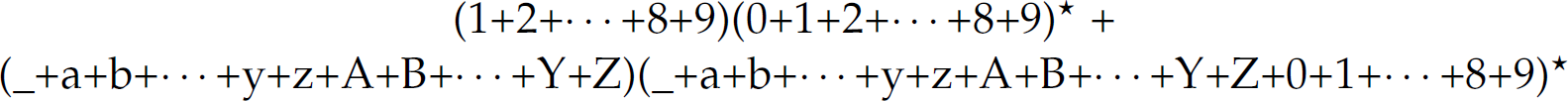
which describes positive integers and legal identifiers in the C programming language.
We can think of an automaton as a simplified computer (Figure 2.1) that, when given a string (i.e., candidate sentence) as input, outputs either yes or no to indicate whether the input string is in the particular language that the machine has been constructed to recognize. In particular, if after running the entire string through the machine one character a time, the automaton is left in an accepting state (i.e., one represented by a double circle, such as states 2 and 3 in Figure 2.1), the string is a sentence. If after running the string through the machine, the machine is left in a non-accepting state (i.e., one represented by a single circle, such as state 1 in Figure 2.1), the string is not a sentence. Formally, a FSA decides a language.
2.3.3 Regular Languages
A regular language is a formal language that can be denoted by a regular expression and recognized by a finite-state automaton. A regular language is the most restrictive type of formal language. A regular expression is a denotational construct for a regular language. In other words, a regular expression denotes sentences from the language it represents. For example, the regular expression opus* denotes the regular language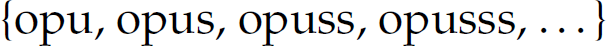 
.
If a language is finite, it can be denoted by a regular expression. This regular expression is constructed by enumerating each element of the finite set of sentences in the language with intervening + metacharacters. For example, the finite language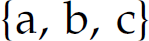 
is denoted by the regular expression 
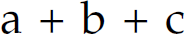. Thus, all finite languages are regular, but the reverse is not true.
In summary, a regular language (which is the most restrictive type of formal language) is denoted by a regular expression and is recognized by a finite-state automaton (which is the simplest model of computation).
Conceptual Exercises for Section 2.3
Exercise 2.3.1 Give a regular expression that defines a language whose sentences are the set of all strings of alphabetic (in any case) and numeric characters that are permissible as login IDs for a computer account, where the first character must be a letter and the string must contain at least one character, but no more than eight.
Exercise 2.3.2 Give a regular expression that denotes the language of five-digit zip codes (e.g., 45469) with an optional four-digit extension (e.g., 45469-0280).
Exercise 2.3.3 Give a regular expression to denote the language of phrases of exactly three words separated by whitespace, where a word is any string of non-whitespace characters and whitespace is any string of spaces or tabs. In your expression, represent a single space character as □ and a single tab character as →. Among the set of sentences that your regular expression denotes are the three underlined substrings in the following string: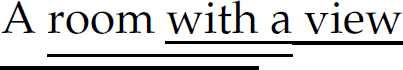 
.
Exercise 2.3.4 Give a regular expression that denotes the language of decimals representing ASCII characters (i.e., integers between between 0–127, without leading 0s for any integer except 0 itself). Thus, the strings 0, 2, 25, and 127 are in the language, but 00, 02, 000, 025, and 255 are not.
Exercise 2.3.5 Give a regular expression for the language of zero or more nested, matched parentheses, where every opening and closing parenthesis has a match of the other type, with the matching opening parentheses appearing before the matching closing parentheses in the sentence, but where the parentheses are never nested more than three levels deep (i.e., no character in the string is ever within more than three levels of nesting). To avoid confusion between parentheses in the string and parentheses used for grouping in the regular expression, use the “l” and “r” characters to denote left (i.e., opening) and right (i.e., closing) parentheses in the string, respectively.
Exercise 2.3.6 Since all finite languages are regular, we can construct an FSA for any finite language. Describe how an FSA for a finite language can be constructed.
1. Sometimes some of the characters in the set of metacharacters are also in the alphabet of the language being defined (i.e.,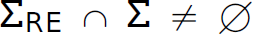 
). In these cases, there must be a way to disambiguate the meaning of the overloaded character. For example, a is used in UNIX to escape the special meaning of the metacharacter following it.
2. The set of metacharacters available to construct regular expressions in most programming languages and UNIX tools has evolved over the years beyond syntactic sugar (for formal regular expressions) and can be used to denote non-regular languages. For instance, the grep regular expression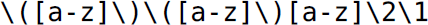 
matches the language of palindromes of five-character, lowercase letters—a non-regular language.
3. More precisely, this finite-state automaton is a nondeterministic finite automaton or NFA. However, the FSA in Figure 2.1 is not a formally a FSA because it has only three transitions, but it should have one for each individual input character that moves the automaton from one state to another. For instance, there should be nine transitions between states 1 and 3—one for each non-zero digit.