40

Vintage Random Number Generators

Éric Jacopin

40.1  Introduction

It will go like this. You are in a hurry and you need to generate random data structures, so you turn to what your favorite programming language provides—it is C++ after all, how could it hurt you? Or maybe it will sneak up on you. You are prototyping and do not want to worry about implementation details. This graphical tool is so practical and elegant, what could go wrong?

The answer to both questions is rand().

rand() can hurt your project because many implementations still use a linear congruential random number generator (LCG), a family of random number generators that were in use as early as 1949 (Lehmer 1949). Many tools still use rand()today to generate integers, real numbers, and Boolean values. Such vintage random number generators are still here because they are fast and simple, not because they work well.

The next section presents rand(). It explains what an LCG is, how it works, and how it can hurt your project when used to generate random Boolean values, for example. The following section presents better LCGs than the ones built into most current-day compilers. Finally, we present a technique that combines two LCGs to provide randomness you can use. Code for this technique will be provided on the book’s website.

40.2  rand(): When Randomness Means Cautiousness

In this section, we explain: Why are linear congruential random number generators linear? Why are they congruential? How can we visualize these properties? What about rand(), how does it work?

A linear congruential random number generator is linear because it uses a linear equation to generate the next random number $x_n$ from the previous random number $x_{n-1}$:

$x_n=a{x}_{n-1}+b$

which gives:

$x_{n\ge 0}=a^n{x}_0+{\displaystyle \sum _{i=0}^{n-1}b{a}^i}$

where x₀ is the seed of the random number generator. Consequently, with $a>0,b\ge 0$ and $x_0>0$ we have:

$\underset{n\to \text{∞}}{\lim }{x}_n=\text{∞}$

If we choose $a=2,b=3$ and $x_0=0$ then $x_{15}=98301$ is the first generated number, which cannot be represented with an unsigned 16-bit integer, whereas $x_{29}=1610612733$ is the largest number, which can be represented by a signed 32-bit integer. We obviously need more than just 29 possible random values.

A linear congruential random number generator is congruential because it frames the generated numbers with the help of a modulus operation:

$x_n=(a{x}_{n-1}+b)\mathrm{mod}m$

For a positive integer m two integers a and b are said to be congruent modulo m when

$a\mathrm{mod}m=b\mathrm{mod}m$

For example, you can choose b = a + m. Consequently, LCGs are periodic random number generators: For some value of n, you will get numbers that have already been generated, in the same order. The following LCG, originally proposed by Derrick Lehmer (Lehmer 1949), has a proven repetition period of 5 882 352:

$x_n=(23x_{n-1})\mathrm{mod}{\text{(10}}^8+\text{1)}$

When b = 0 the LCG is called multiplicative and one must be careful with the seed, since $x_0=0$ will force $x_{n>0}=0$ (that is, once one value is 0, then all following values will also be 0), which is certainly not random. Consequently, seeds for multiplicative LCGs must be chosen in the range [1,m)—that is, at least equal to 1 and strictly less than $m$. To avoid $x_n=0$ becoming true for some other generated value, multiplicative LCGs are designed so that only $x_{n-1}=m$ would give $x_n=0$, which is impossible by definition since all generated values are strictly less than the modulus $m$.

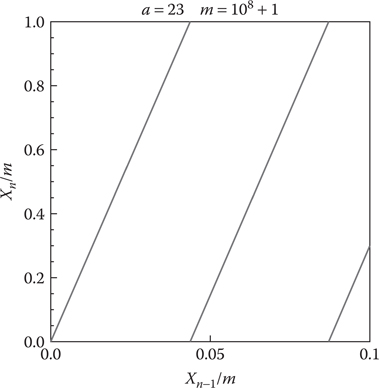
Both linearity and periodicity of LCGs can be easily visualized by plotting the points made of the pairs $(x_{n-1},x_n)$ of successive numbers that have been generated; if we further divide the generated numbers by $m$, we get a normalized plot over the unit range (0,1), of the linear and repetitive behavior of an LCG, as shown in Figure 40.1.

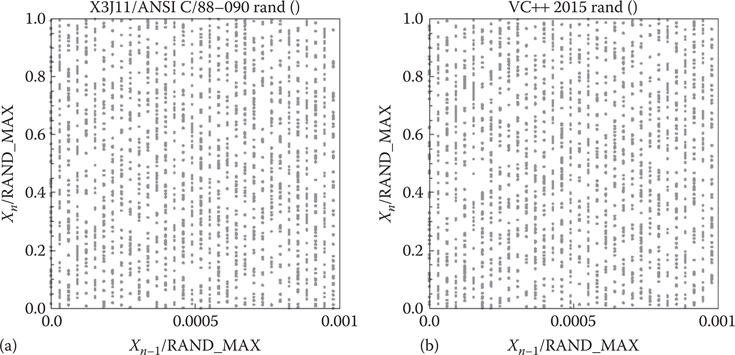
All LCGs repeat themselves for some value of $n$, including rand(). Visualizations for ANSI C (X3J11 1988) and Visual C++ 2015 are shown in Figure 40.2.

Figure 40.1
$a=23,b=0$ and $m=10^8+1$ has a repetition period of 5 882 352.

Figure 40.2
(a) rand() from ANSI C. (b) Visual C++ 2015’s rand().

Here is the portable implementation of rand() from ANSI C (a = 1103515245, b = 12 345 $andm=32768):$

And here is the LCG which is still used by Visual Studio’s C and C++ (Lomont 2008):

$x_n=(214013x_{n-1}+2531011)\mathrm{mod}{2}^{31}$

Note that as $b\ne 0$ for both previous LCGs, the seed $x_0$ can safely be chosen in the range (0,m) (i.e., greater or equal to 0 and strictly less than $m$) and $x_{n-1}=561051201$ is the only value in the range $(0,2^{31})$ such that:

$(214013x_{n-1}+2531011)\mathrm{mod}{\text{2}}^{31}=0$

The $ith$ bit of this LCG has a period of $2^i$ (L’Écuyer 1990), highlighted in gray in the following $(x_0=0)$

$x_{n\ge 0}\&1=1,0,1,0,1,0,\mathrm{\dots }$

$x_{n\ge 0}\&2=1,1,0,0,1,1,0,0,1,1,0,0,\mathrm{\dots }$

$x_{n\ge 0}\&4=0,0,1,1,1,1,0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,1,0,0,\mathrm{\dots }$

$x_{n\ge 0}\&8=0,1,0,0,0,1,1,1,1,0,1,1,1,0,0,0,0,1,0,0,0,1,1,1,1,0,1,1,1,0,0,0,\mathrm{\dots }$

Since $2^{31}=2^{16+15}=2^{16}\times 2^{15},$ Microsoft’s implementation of rand() divides $x_n$ by $2^{16}$ which deletes the 16 least significant (and most rapidly repeated) bits so that rand() returns values strictly less than $2^{15}=32768=1+$ RAND_MAX. But the 17^th bit nevertheless has a period of $2^{17}$ and so on for the higher order bits of the numbers generated by rand().

To illustrate one of the common pitfalls of working with rand(), we end this section with a discussion on generating random Boolean values. Integer values 0 and 1 are typically used to represent Boolean false and true, respectively, so it makes sense to generate 0 and 1 values with rand() using a modulus operation:

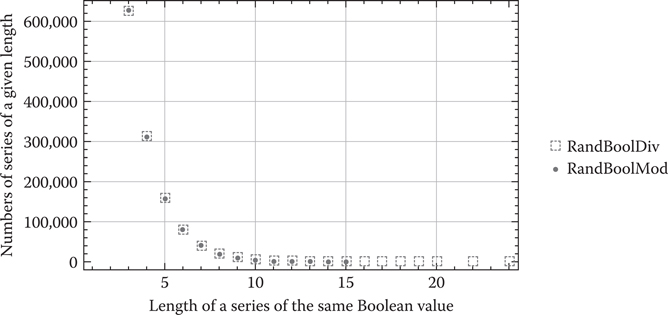
Figure 40.3
Which use of rand() do you want to generate Boolean values?

It is also possible to divide rand() by (RAND_MAX+1), multiply by 2, truncate the result and return the result as a Boolean value, which is the method used by the Unreal Engine 4:

Both methods are valid; however, as predicted by the discussion above on the periodicity of the $ith$ bit and as shown in Figure 40.3 above, RandBoolDiv() will generate longer series of the same Boolean value than RandBoolMod(), thus increasing the perception that your game is cheating (Rabin 2004). As a result, on one hand the series of random Boolean values generated with rand() has a smaller period than that of a better LCG and on the other hand there are very long subseries with the same Boolean value, that is either false or true.

40.3  Vintage LCGs You Could Use

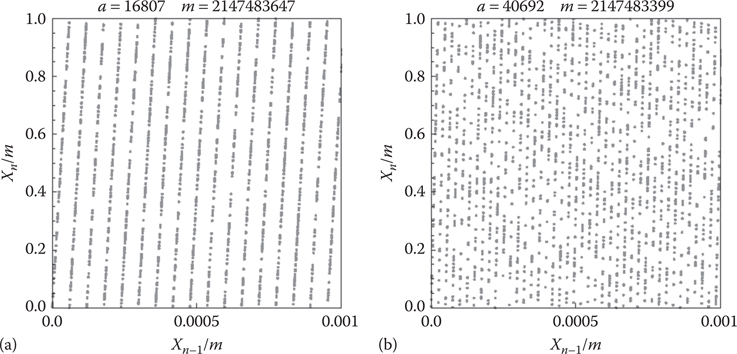
Over the years, many empirical and theoretical tests have been developed to assess the performance of LCGs, thus pushing forward the search for better LCGs. We begin with two LCGs reported by NASA as two useful uniform random number generators with very satisfactory performance (Howell and Rheinfurth 82, page 2):

$x_n=(16807x_{n-1})\mathrm{mod}{\text{(2}}^{31}-\text{1)}$

$x_n=(29903947x_{n-1})\mathrm{mod}{\text{(2}}^{31}-\text{1)}$

Figure 40.4
(a) Minimum standard LCG. (b) One of the best known LCGs.

The LCG with $a=16807$ and $m=2^{31}-1$ is sometimes considered the minimal standard (Park and Miller 1988) for LCGs and both exhaustive search, and theoretical work has shown that for $m=2^{31}-1$, the choice of $a=16807$is one of the best possible values (L’Écuyer 1988) for the multiplier $a.$ Other good choices include $a=742938285$, $a=950706376$and $a=630360016$. An even better option is the LCG:

$x_n=(40692x_{n-1})\mathrm{mod}(2147483399)$

which is reported to achieve excellent performance (L’Écuyer 1988). Both of these LCGs are visualized in Figure 40.4.

40.4  Combined LCGs: LCGs You Can Use

Although the LCGs in Figure 40.4 are getting better and better, they still suffer from the same inherent problems as rand(). One way to do significantly better is to combine the output of multiple LCGs. Assume two distinct LCGs:

$x_{1,n}=(a_1{x}_{1,n-1}+b_1)\mathrm{mod}{m}_1$

$x_{2,n}=(a_2{x}_{2,n-1}+b_2)\mathrm{mod}{m}_2$

Here is how to combine $x_{1,n}$ and $x_{2,n}$ into one LCG (L’Écuyer 1988):

$x_n=(x_{1,n-1}-x_{2,n-1})\mathrm{mod}(m_1-1)$

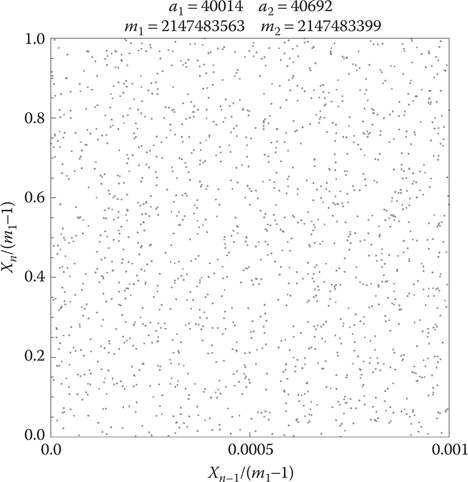
In theory you can combine as many LCGs as you want (L’Écuyer 1988) (with obvious runtime costs), but two are enough to provide far better performance than one LCG alone. As you can see in Figure 40.5, a combination of two LCGs does not show the linear and congruential properties we have seen in Figures 40.1, 40.2, and 40.4. Although not perfect, combined LCGs achieve the best randomness that LCGs can provide. If you want to keep using vintage random number generators, combined LCGs are the approach that you should use.

Figure 40.5
Combined LCGs for the randomness you should use.

The code used to generate Figure 40.5 is available on the website, and can be plugged directly in to your game.

40.5  Conclusion

Let us face it: stop using rand(). This can be difficult if not impossible as rand() can be hidden in other random functions (such as those built into a third-party game engine), but the effort is worth it. For example, consider combining LCGs as presented in Section 40.4!

Finally, please, take the time to read the papers published on the topic of random number generators for game programming (Lecky-Thompson 2004, Isensee 2001, Jones 2004, Lomont 2008, Rabin 2008), and game artificial intelligence in particular (Freeman-Hargis 2004, Rabin 2004, Rabin et al. 2014).

Acknowledgments

Thanks to Marjan Petkovski for his comments, to Elric Jacquart for generating millions of random numbers, and to Kevin Dill for his work editing this chapter.

References

X3J11. 1988. Draft ANSI C Standard 88-090. http://flash-gordon.me.uk/ansi.c.txt (accessed February 15, 2017).

Freeman-Hargis, J. 2004. The statistics of random numbers. In AI Game Programming Wisdom 2, ed. S. Rabin. Hingham, MA: Charles River Media, pp. 59–70.

Howell, L. W. and M. H. Rheinfurth. 1982. Generation of pseudo-random numbers. Nasa Technical Paper 2105, 27 pages. Hampton, VA.

Isensee, P. 2001. Genuine random number generator. In Game Programming Gems 2, ed. M. DeLoura. Hingham, MA: Charles River Media, pp. 127–132.

Jones, T. 2004. Zobrist hash using the mersenne twister. In Game Programming Gems 4, ed. A. Kirmse. Hingham, MA: Charles River Media, pp. 141–146.

Lecky-Thompson, G. W. 2004. Predictable random numbers. In Game Programming Gems, ed. M. DeLoura. Hingham, MA: Charles River Media, pp. 133–140.

Lehmer, D. H. 1949. Mathematical methods in large scale computing units. In Proceedings of the 2nd Symposium on Large Scale Digital Calculating Machinery. Harvard University Press, pp. 141–146.

L’Écuyer, P. 1988. Efficient and portable combined random number generator. Communications of the ACM 31(6):742–749, 774.

L’Écuyer, P. 1990. Random numbers for simulations. Communications of the ACM 33(10):85–97.

Lomont, C. 2008. Random number generation. In Game Programming Gems 7, ed. S. Jacobs. Hingham, MA: Charles River Media, pp. 113–125.

Park, S. and K. Miller. 1988. Random number generators: Good ones are hard to find. Communications of the ACM 31(10):1192–1201.

Rabin, S. 2004. Filtered randomness for AI decisions and game logic. In AI Game Programming Wisdom 2, ed. S. Rabin. Hingham, MA: Charles River Media, pp. 71–82.

Rabin, S. 2008. Using Gaussian randomness to realistically vary projectile paths. In Game Programming Gems 7, ed. S. Jacobs. Hingham, MA: Charles River Media, pp. 199–204.

Rabin, S., J. Goldblatt and F. Silva. 2014. Gaussian randomness, filtered randomness, and Perlin noise. In Game AI Pro, ed. S. Rabin. Hingham, MA: Charles River Media, pp. 29–43.