Appendix 5

Perfect and Figured Numbers

Perfect Numbers

One classification of numbers attributed to the Pythagoreans involves comparing a number with the sum of its proper divisors—that is, excluding the number itself. If this sum is smaller than the number, the latter is called defective; if it is greater, the number is excessive. For example, 15 is defective, since 1 + 3 + 5 < 15, and 24 is excessive (24 < 1 + 2 + 3 + 4 + 6 + 8 + 12). A number is perfect if it’s neither defective nor excessive, in other words, if it is equal to the sum of its proper divisors. Examples of perfect numbers are 6 (= 1 + 2 + 3) and 28 (= 1 + 2 + 4 + 7 + 14).

In the final proposition of Book IX of his Elements, Euclid provided a recipe for constructing perfect numbers: if 2ⁿ − 1 is prime, then the product 2ⁿ − 1 (2ⁿ − 1) is a perfect number. The two examples of perfect numbers above arise from Euclid’s formula by taking n = 2 and n = 3. The next two perfect numbers are 496 (for n = 5) and 8128 (n = 7).

If you were left with the impression that Euclid’s formula will readily lead to the discovery of plenty of perfect numbers, consider this: all the perfect numbers the Greeks ever knew were the four mentioned above, and it was not until the fifteenth century that another one was added to the list (2¹² (2¹³ − 1)). Today, only about forty perfect numbers are known, and their fascinating theory still contains many simple but unanswered questions, such as: Is there an odd perfect number? Are there infinitely many perfect numbers?

Triangular Numbers

It was common practice among the Pythagoreans to represent numbers using dots or pebbles arranged in geometrical patterns. The simplest of these are the triangular numbers.

The triangular number 15

Pythagoras is credited with discovering that triangular numbers arise by adding n consecutive natural numbers (starting from 1): 1 + 2 + 3 + . . . + n. For example, 1 + 2 + 3 + 4 + 5 produces the triangular number 15, represented as a 15-dot triangle of side 5, as in the figure above.

Square Numbers

These are obtained when n successive odd natural numbers are added: 1 + 3 + 5 + 7 + . . . + (2n − 1).

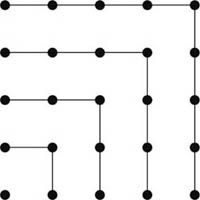
The square number 25

That the above sum always produces a square number can be seen either geometrically (as shown in the figure, where each successive odd number, represented in the shape of an “L,” increases the side of the square by one) or algebraically, using the identity

1 + 3 + 5 + . . . + (2n –1) = n².