Chapter 16
THE HUNT
She had been introduced to Jule by Trench as “Professor Hirsch, an authority on ancient Greece.” And, after the customary exchange of polite greetings, Trench had added: “Professor Hirsch is presently writing a book about Pythagoras. She will be your resource person on him and his school.”
Her full name was Laura Eva Hirsch. She was born in the former German Democratic Republic, where she studied Greek history and mythology before escaping to the United States as a political refugee with the help of a diplomat friend. In 1983, she received her PhD in classical studies from the University of Illinois. She stayed on at her alma mater as a teacher, moving quickly through the ranks until she became a full professor in 1989. Now in her late forties, she was a tall, slender woman with an intelligent if not attractive face, her dark brown hair and black eyes accentuating the whiteness of her skin.
It was Saturday morning. Jule and the professor were alone in a large room with tall windows overlooking the park at the back of the house. A blanket of fresh snow extended into the distance, interrupted only at the far end by a dark wall of pine trees. High above the trees, a few small clouds floated against the pale blue sky like cotton islands in a vast, calm sea. Jule had had dinner and breakfast served in his room by a silent and unsmiling old lady, so this was his first contact with someone other than Trench or Leonard Richter.
The professor spoke first. “I’ll be assisting you with anything you wish to know about Pythagoras and his disciples,” she said to Jule, who noticed that she spoke with a slight German accent. “Think of me as a kind of human Google,” she added with a smile.
“I’ll need all the help I can get,” replied Jule, smiling back, happy to learn that the professor didn’t seem to take herself too seriously. “Why don’t you begin with an introduction to the man and his doctrines, anything you would care to tell me for starters?” he suggested, flipping open his notebook.
“All right,” she said, with an approving nod. She sat back in her leather chair and, after a few moments’ reflection, began her lecture.
“In his time, Pythagoras was revered as a man of exceptional wisdom, almost as a demigod. But today he is remembered primarily for the famous theorem named after him, although the result was known to the Babylonian and Indian civilizations centuries before his birth. I remember learning it by rote as a youngster—in German, of course, my mother tongue: ‘In a right-angled triangle, the square of the hypotenuse equals the sum of the squares of the two other sides.’ ”
Jule half-raised his hand, like a student trying to get the teacher’s attention. Laura Hirsch smiled and said, “Yes?”
“You just said that Pythagoras’ famous result was known to more ancient civilizations. Do you mean then that Pythagoras’ theorem is not really Pythagoras’?”
“No, I didn’t mean that, but the question of ‘ownership’ is a difficult one, especially when the claimants have been dead for thousands of years and what few records remain are open to different interpretations. Take, for example, a fragment of a Babylonian clay tablet dating from 1700 BC and kept at some museum—in New York, I believe. It consists of four columns of numbers, written in cuneiform script and in the system of numeration the Babylonians used. According to modern scholars, it is essentially a table of so-called Pythagorean triples, that is, numbers a, b, and c such that a2 = b2 + c2—actually, only the columns corresponding to the values of a and b appear on the extant piece of the tablet. One may then assume that the Babylonians knew the famous theorem we attribute to Pythagoras. But did they really?”
“I see your point,” said Jule. “It’s not absolutely clear that those numerical equations arose from their knowledge of the geometry of right-angled triangles; I mean, that they were actually listing the relationship between the hypotenuse, a, and the sides, b, c of right-angled triangles. They could have been merely showing examples of an arithmetical curiosity: square numbers that are sums of two square numbers.”
“It’s possible. But although the table doesn’t explicitly mention any geometrical relationship, the headings of the columns for a and b read ‘square-side of the diagonal’ and ‘square-side of the width,’ respectively, so they could well have known the theorem after all.
“Besides, there is another Babylonian tablet, with a diagram and three numbers written on it, which might suggest the Babylonians were aware of a visual proof of the theorem for isosceles triangles.
“As for Indian mathematics, the evidence is perhaps more compelling. Baudhâyana was an Indian priest and mathematician who lived around 800–600 BC. He probably was not interested in mathematics for its own sake but for its use in the construction of altars needed for sacrifices to the gods and other religious rites. For these sacrifices to be successful and the gods to grant the people’s wishes of good health, abundance of food, and so forth, the altar had to be built according to very precise measurements. Baudhâyana’s Sulba Sutra or ‘Rule of Chords,’ written in Sanskrit and without using any mathematical symbols, is a collection of mathematical results and geometric constructions stated without proof. Among these, we find the following statement.” She searched through her papers. “Here we are: A rope stretched along the length of the diagonal produces an area which the vertical and horizontal sides make together.”
“That’s amazing!” Jule cried out in admiration. “It’s essentially the general form of what we call the Pythagorean theorem. I read that as a young man Pythagoras traveled to India. Could he possibly have learned about the result over there?”
The professor answered in an indirect way: “It’s not certain that Pythagoras traveled as far as India, although it is well established that he visited Egypt. In my opinion, such a fundamental mathematical result, especially one with obvious practical applications—carpenters still use it today for making square corners—would have been discovered sooner or later in any advanced civilization, so it may well have more than one discoverer.
“Actually,” interrupted Jule, “what carpenters really use is not the theorem itself but its converse: if a2 + b2 = c2, then the triangle is right-angled—a distinction that is lost on most people.”
“I know, I was one of those people,” Ms. Hirsch confessed with a nod. “The Chinese too have claimed the paternity of the theorem,” she went on. “There exists a very ancient Chinese mathematical text* dating at least from the time of Confucius in the sixth century BC, if not earlier, with a drawing of a square askew within a larger gridded one, and a commentary accompanying it. Together, they provide a visual proof of the theorem for the 3, 4, 5 triangle.”
“Why then did the theorem become associated with the name of Pythagoras?”
“The truth is we really don’t know. The earliest reliable source is Plutarch, a Greek writer from the first century AD, who reported that according to a certain Apollodorus the logician, Pythagoras offered a splendid sacrifice of oxen to celebrate his discovery that ‘the square of the hypotenuse of a right-angled triangle was equal to the squares of the sides containing the right angle,’ and that the event inspired an epigram:
When the great Samian sage his noble problem found
A hundred oxen with their life-blood dyed the ground.
However, such a ‘celebration’ appears most unlikely, given the Pythagoreans’ convictions against killing animals and eating animal flesh.”
“How about the proof of the theorem, then?” asked Jule, attacking the question from a different angle. “There exist hundreds of different arguments establishing the validity of the proposition, but how did Pythagoras prove it—if indeed he did?”
“I know there are hundreds of proofs,”† said Ms. Hirsch before answering Jule’s question, “including one in the nineteenth century from a certain James A. Garfield, who would later become president of the United States. But how Pythagoras might have convinced himself of the truth of his proposition is something we don’t know. In fact, we must first elucidate the notion of what constituted in his time a mathematical proof.”
“The famous British mathematician Michael Atiyah once said that proof is the glue that holds mathematics together,” observed Jule. “But the concept of proof evolved over time. In 1988, the nonexistence of a projective plane of order 10, a two-century-old question in geometry, was finally settled—in the negative—using a supercomputer to carry out certain parts of the proof. Problem was, only a computer could check those parts of the proof. As the New York Times put it: ‘Is a maths proof a proof if no one can check it?’ ”
“Let’s get back to the Greeks, if you will.” Eva Hirsch hadn’t appreciated the digression into twentieth-century mathematics. She searched on her laptop for a few moments. “Here it is. These are excerpts from a book on the beginnings of Greek mathematics. Read for yourself.” She handed him the laptop.
The most substantial difference between Greek and Oriental sciences is that the former is an ingenious system of knowledge built up according to the method of logical deduction, whereas the latter is nothing more than a collection of instructions and rules of thumb, often accompanied by examples, having to do with how some particular mathematical tasks are to be carried out. [ . . . ]
The mathematical term for proof and to prove is the Greek verb 
, and it seems most likely that right from the start this verb meant “to point out” in both a figurative and a literal sense, and hence also “to explain”. [ . . . ] Some scholars, without making any reference to this verb, have stressed the importance of visual evidence in early Greek mathematics. This suggests the idea that the earliest “proofs” may have involved some kind of “pointing out” or “making visible” of the facts; in other words, 
may have become a technical term for “proof” in mathematics because “to prove” meant originally “to make the truth (or falsity) of a mathematical statement visible in some way” [ . . . ].
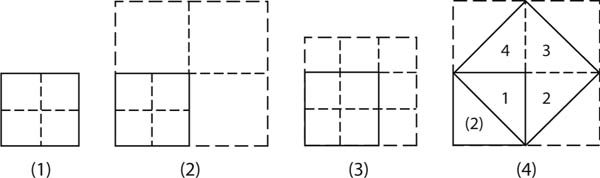
Here is an example of mathematics teaching in antiquity that seems to support our conjecture. It is the passage from Plato’s Meno where Socrates asks a slave how the area of a square with sides two units long can be doubled without altering its shape. He then draws a diagram [see (1) in the figure] showing the square that is to be doubled. After the slave answers that the square will perhaps be doubled by doubling the length of its sides, Socrates draws a second diagram (2) to show that a square whose sides are twice as long as those of the original one, has an area four times its size. He then goes on to draw a third diagram (3) showing that a square whose sides are three units long, has an area of nine square units, and hence cannot be the double of the original one. Finally in his fourth diagram (4) he shows that the square on the diagonal has exactly twice the original area.
I think this passage from Plato provides an excellent illustration of the way in which statements were verified at an early stage in the development of Greek mathematics, i.e., it tells us how propositions were “proved” in the archaic sense of this word. The proposition that has been illustrated and “proved” above, can be formulated as follows: “A square constructed on the diagonal of another has twice the other’s area.” [ . . . ]
On the other hand, the proofs in Euclid’s Elements [some two centuries later] are already in a polished form. [ . . . ] He is less interested in making his propositions visually evident than in convincing the reader of their truth by a train of abstract arguments.
Jule finished reading and remained silent, staring at the computer screen. A minute went by before Eva Hirsch finally broke the silence: “So? What do you think?”
Jule answered with a question: “Was Socrates a contemporary of Pythagoras?”
“No, he was born some seventy years after Pythagoras’ death. Why do you ask?”
“Because his solution of the problem is also a very simple proof of Pythagoras’ theorem, albeit in the particular case of an isosceles triangle.”
“How’s that?” She seemed to have been caught by surprise.
“Come and take a look at Socrates’ fourth diagram.” She moved over beside him.
“The diagonal of the square is also the hypotenuse of a right-angled triangle whose two other sides are the sides of the square,” Jule explained, as his finger traced out the triangle on the screen. “So the square on the diagonal is the square on the hypotenuse, and Socrates showed that its area is twice that of the original square, in other words, equal to the sum of the squares on the two other sides.”
It only took the classics professor a moment to grasp Jule’s argument. “I’m impressed,” she said, turning her head to look at him.
Jule ignored the compliment. “I bet Pythagoras used a similar geometric construction to convince himself of the truth of the proposition in the general case. By the way, your Indian mathematician who stated the theorem eons ago—‘a rope stretched along the diagonal . . . ’—never mentioned a rectangle, so maybe his statement was only about the particular case of the square too.”
“You’re right—and not the first one to have raised the question. But let’s move on. I’m supposed to be telling you all about Pythagoras and his school and I’ve hardly begun.”
She went back to her chair and resumed her lecture.
“For Pythagoras, the intellect was the most important human faculty, for it can lead to a form of knowledge that surpasses any other in depth and certainty. ‘Let reason, the gift divine, be thy highest guide,’ he taught. His vision of nature was based on the principle that numbers rule the world, and is often condensed in the dictum ‘All is number.’ He seemed to have reached this sweeping conclusion after observing that musical intervals pleasing to the ear, such as octaves, fifths, and fourths, as they are now called, come from plucking two taut strings whose lengths are in the same ratio as two whole numbers—2 to 1, 3 to 2, and 4 to 3, respectively. Such a bold generalization may appear naïve to us, but what if the Pythagoreans had found evidence in support of their belief? What if they had discovered that the cosmos is a kind of infinite hologram? Then, just as a small fragment of a hologram contains all the features of the whole, so all the secrets of the universe may be hidden in any tiny speck of it—a crawling insect, a child’s smile, or a vibrating string.
“Echoes of the Pythagorean tenet may still be found 2,000 years later in Galileo’s belief that the Book of Nature is written in the language of mathematics. In fact, many famous scientists, from Kepler to Einstein, to name only two, shared Pythagoras’ vision of a universe ruled by numbers and harmony, one whose inner workings could be grasped by uncovering the underlying mathematical relationships.
“Kepler’s discovery at the beginning of the seventeenth century of the laws of planetary motion was guided by his firm belief in Pythagorean principles. For him, geometry had provided God with a model for the Creation; and the orbital speeds of planets were a reflection of consonant musical intervals, so that, in their periodic journey around the Sun, the heavenly motions produced the ‘music of the spheres,’ perceived not by the ear but by the intellect.
“As for Einstein, not only did he reject the probabilistic foundations of quantum mechanics on the basis that ‘God does not play dice with the world,’ but he also wrote that a scientist may count as a Platonist or Pythagorean if he considers the viewpoint of logical simplicity as an indispensable and effective research tool, a viewpoint that he had himself adopted.
“But after having discovered galaxies and genes, quantum phenomena and chaotic systems, and caught a glimpse at the complexity of biological processes, we now know that the universe is not as simple as ‘all is number.’ And yet . . .
“It is thanks to numbers that we can swiftly store, transmit, and reproduce not just information in various forms but also sounds and images. In a very real sense, a CD, DVD, digital picture, or movie is a sequence of numbers—the 0s and 1s of its binary code. Decisions affecting the fate of most individuals are based on statistics, a sophisticated form of numerical manipulation. Numbers are also used in subtle ways to control, mislead, or deceive, as when complex concepts are reduced to a single number, when ‘intelligence’ is identified with IQ, or the health of that intricate reality we call ‘the economy’ is expressed numerically as gross national product.
“Numbers alone might not rule the world of nature created by God, as Pythagoras believed—and in that sense he has been proven wrong—but they increasingly reign over the human-made world that is life in a modern society. That’s Pythagoras’ revenge.”
“Is that also the title of your book?” asked Jule.
“Tentatively, yes,” she replied, “but editors always have the last word on such matters.”
Professor Hirsch went on with her lecture for a good three hours, occasionally reading from a thick file of notes or her computer screen and interrupted every once in a while by a question from Jule. They hardly noticed the old woman when she came in to leave a tray with coffee, sandwiches, and some fruit.
Trench dropped in at around four o’clock. He filled them in on the mechanics and other details of the operation known as “The Hunt”: finding Pythagoras reincarnate and bringing him to the Temple. Jule and Laura would be in charge of the “finding” part of the undertaking (who and where is he), while Rocky and Houdini would be called in for the “bringing” phase, when—and if—Jule and Laura succeeded.
For the coming weeks—or months—they would stay at a hotel in the city and work at Richter’s place in Highland Park, where an office had been equipped with the latest technology.
Their task was not an easy one, to say the least, not to mention the fact that they could very well be chasing a ghost if the story of Pythagoras’ reincarnation turned out to be only a myth, a legend like so many other ancient tales. Blinded by their faith, the members of the Neo-Pythagorean sect hadn’t even considered such a possibility—and Laura and Jule were not to contemplate it either, as Trench had made clear to them—so the next question was where to start.
*The Zhou bi suan jing.
†See appendix 4 for a visual proof of the theorem.