Image Gradients

To do better than raw pixel values, we have to somehow “organize” the pixels into more informative units. Differences between neighboring pixels are often very useful. Pixel values usually differ at the boundary of objects, when there is a shadow, within a pattern, or on a textured surface. The difference in value between neighboring pixels is called an image gradient.

The simplest way to compute the image gradient is to separately calculate the differences along the horizontal (x) and vertical (y) axes of the image, then compose them into a 2D vector. This involves two 1D difference operations that can be handily represented by a vector mask or filter. The mask [1, 0, –1] takes the difference between the left neighbor and the right neighbor or the up-neighbor and the down-neighbor, depending on which direction we apply the mask. There are 2D gradient filters as well, but for the purpose of this example, the 1D filter suffices.

To apply a filter to an image, we perform a convolution. It involves flipping the filter and taking the inner product with a small patch of the image, then moving to the next patch. Convolutions are very common in signal processing. We’ll use ∗ to denote the operation:

The x and y gradients at pixel (i,j) are:

Together, they form the gradient:

A vector can be completely described by its direction and magnitude. The magnitude of the gradient is equal to the Euclidean norm of the gradient $\left(\sqrt{g_x^2+g_y^2}\right)$, which indicates how much the pixel values change around the pixel. The direction or orientation of the gradient depends on the relative size of the change in the horizontal and vertical directions; it can be computed as $\theta =arctan\left(\frac{g_y}{g_x}\right)$. Figure 8-2 illustrates these mathematical concepts.

Figure 8-3 illustrates examples of the simple image gradient that is composed of the vertical and horizontal gradients. Each example is an image of nine pixels. Each pixel is labeled with a grayscale value. (Smaller numbers correspond to a darker color.) The gradient for the center pixel is shown below each image. The image on the left contains horizontal stripes, where the color only changes vertically. Therefore, the horizontal gradient is zero and the gradient is nonzero vertically. The center image contains vertical stripes; therefore, the horizontal gradient is zero. The image on the right contains diagonal stripes and the gradient is also diagonal.

Figure 8-2. Illustration of the definition of an image gradient

Figure 8-3. Simple examples of the image gradient

The definition works on synthetic toy examples. But would it work well on a real image? In Example 8-1, we examine this using a picture of a cat from scikit-image, shown in Figure 8-4 with its horizontal and vertical gradients.  Since the gradients are computed at every pixel location of the original image, we end up with two new matrices, each of which can be visualized as an image.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from skimage import data, color

### Load the example image and turn it into grayscale
>>> image = color.rgb2gray(data.chelsea())

### Compute the horizontal gradient using the centered 1D filter.
### This is equivalent to replacing each non-border pixel with the
### difference between its right and left neighbors. The leftmost
### and rightmost edges have a gradient of 0.
>>> gx = np.empty(image.shape, dtype=np.double)
>>> gx[:, 0] = 0
>>> gx[:, -1] = 0
>>> gx[:, 1:-1] = image[:, :-2] - image[:, 2:]

### Same deal for the vertical gradient
>>> gy = np.empty(image.shape, dtype=np.double)
>>> gy[0, :] = 0
>>> gy[-1, :] = 0
>>> gy[1:-1, :] = image[:-2, :] - image[2:, :]

### Matplotlib incantations
>>> fig, (ax1, ax2, ax3) = plt.subplots(3, 1, 
...                                     figsize=(5, 9), 
...                                     sharex=True, 
...                                     sharey=True)

>>> ax1.axis('off')
>>> ax1.imshow(image, cmap=plt.cm.gray)
>>> ax1.set_title('Original image')
>>> ax1.set_adjustable('box-forced')

>>> ax2.axis('off')
>>> ax2.imshow(gx, cmap=plt.cm.gray)
>>> ax2.set_title('Horizontal gradients')
>>> ax2.set_adjustable('box-forced')

>>> ax3.axis('off')
>>> ax3.imshow(gy, cmap=plt.cm.gray)
>>> ax3.set_title('Vertical gradients')
>>> ax3.set_adjustable('box-forced')

Figure 8-4. Gradients of an image of a cat

Note that the horizontal gradient picks out strong vertical patterns such as the inner edges of the cat’s eyes, while the vertical gradient picks out strong horizontal patterns such as the whiskers and the upper and lower lids of the eyes. This might seem a little paradoxical at first, but it makes sense once we think about it a bit more. The horizontal (x) gradient identifies changes in the horizontal direction. A strong vertical pattern spans multiple y pixels at roughly the same x position. Hence, vertical patterns result in horizontal differences in pixel values. This is what our eyes detect as well. 

Gradient Orientation Histograms

Individual image gradients can pick out minute differences in an image neighborhood. But our eyes see bigger patterns than that. For instance, we see an entire cat’s whisker, not just a small section. The human vision system identifies contiguous patterns in a region, so we still have more work to do to summarize the image gradients in a neighborhood.

How exactly might we summarize vectors? A statistician would answer, “Look at the distribution!” SIFT and HOG both take this path. In particular, they compute (normalized) histograms of the gradient vectors as image features. A histogram divides data into bins and counts how many data points are in each bin; this is an (unnormalized) empirical distribution. Normalization ensures that the counts sum to 1. The mathematical language is that it has unit ${\ell }^1$ norm.

An image gradient is a vector, and vectors can be represented by two components: the orientation and magnitude. So, we still need to decide how to design the histogram to take both components into account. SIFT and HOG settled on a scheme where the image gradients are binned by their orientation angle θ, weighted by the magnitude of each gradient. Here is the procedure:

1. Divide 0°–360° into equal-sized bins.

2. For each pixel in the neighborhood, add a weight w to the bin corresponding to its orientation θ. w is a function of the magnitude of the gradient and other relevant information. For instance, that information might be the inverse distance of the pixel to the center of the image patch. The idea is that the weight should be large if the gradient is large, and pixels near the center of the image neighborhood matter more than pixels that are farther away.

3. Normalize the histogram.

Figure 8-5 provides an illustration of a gradient orientation histogram of 8 bins composed from an image neighborhood of 4 × 4 pixels.

Figure 8-5. Illustration of a gradient orientation histogram of 8 bins based on gradients from a 4 × 4 square cell of pixels

There are, of course, a number of knobs to tweak in the basic gradient orientation histogram algorithm, as well as some optional bells and whistles. As usual, the right settings are probably highly dependent on the particular images one wants to analyze.

Let’s examine next some of the decisions to make and the effects these can have on your model.

SIFT Architecture

The SIFT pipeline requires quite a number of steps. HOG is slightly simpler but follows many of the same basic steps, such as creating a gradient histogram and normalization. Figure 8-6 illustrates the SIFT architecture. Starting from a region of interest in the original image, we first divide the region into a grid. Each grid cell is then further divided into subgrids. Each subgrid element contains a number of pixels, and each pixel produces a gradient. Each subgrid element produces a weighted gradient estimate, where the weights are chosen so that gradients outside of the subgrid element can contribute. These gradient estimates are then aggregated into an orientation histogram for the subgrid, where gradients can have weighted votes as described previously. The orientation histograms for each subgrid are then concatenated to form a long gradient orientation histogram for the entire grid. (If the grid is divided into 2 × 2 subgrids, then there will be 4 gradient orientation histograms to concatenate into 1.) This is the feature vector for the grid, which then goes through a normalize–threshold–normalize process. First, the vector is normalized to have unit norm. Then, individual values are clipped to a maximum threshold. Finally, the thresholded vector is normalized again. This is the final SIFT feature descriptor for the image patch.

Figure 8-6. SIFT architecture—steps to produce a feature vector for a region of interest in the original image

Fully Connected Layers

At the core of all neural networks are linear functions of the input. Logistic regression, which we encountered in Chapter 4, is an example of a neural network. A fully connected neural network is simply a set of linear functions of all of the input features. Recall that a linear function can be written as an inner product between the input feature vector and a weight vector, plus a possible constant term. A collection of linear functions can be represented as a matrix-vector product, where the weight vector becomes a weight matrix (W).

The mathematical definition of a fully connected layer is:

where each row of W is a weight vector that maps the entire input vector x into a single output in z. b is a vector of scalars representing the constant offset (or bias) for each neuron.

The fully connected layer is so named because every input can be used in every output. Mathematically, this means that there are no restrictions on the values in the matrix W. (As we will soon see, a convolutional layer makes use of only a small subset of inputs for each output.) Pictorially, a fully connected neural net can be represented by a complete bipartite graph where every node in the input is connected to every node in the output (see Figure 8-7).

Figure 8-7. A fully connected neural network, represented as a graph

Fully connected layers contain the maximum possible number of parameters (#input × #output)—hence, they are considered expensive. Such dense connection allows the network to detect global patterns that could involve all inputs. The last two layers of AlexNet are fully connected for this reason. The outputs are still independent from each other, conditioned on the inputs.

Convolutional Layers

In contrast to fully connected layers, a convolutional layer uses only a subset of inputs for each output.  The transformation “moves” across the input, producing outputs using a few features at a time. For simplicity, one can use the same weights for different sets of input, instead of learning new weights for each set of input.

Mathematically, the convolution operator takes two functions as input and produces one function as output. It flips one of the input functions, moves it across the other function, and outputs the total area under the multiplied curves at each point:

The way to compute total area under a curve is to take its integral. The operator is symmetric in the inputs, meaning that it does not matter whether we flip the first input or the second; the output is the same.

We’ve already seen an example of simple convolution, when we looked at image gradients (“Image Gradients”). But the mathematical definition of convolution may still appear to be somewhat convoluted. There is reason to its madness. It’s easiest to explain the intuition behind convolution using an example from signal processing.

Imagine that we have a little black box. To see what the black box does, we pass a single unit of stimulus through it. We record whatever the output looks like on a little sheet of paper. We wait until there is no more response to the original stimulus. The resulting function over time is the response function; let’s call it g(t).

Imagine now that we have some crazy wild signal f(t), which we proceed to feed through the black box. At time t = 0, f(0) interacts with the black box and produces f(0) multiplied by g(0). At time t = 1, f(1) enters the black box and gets multiplied by g(0). At the same time, the black box continues to respond to the previous signal f(0), which is now multiplied by g(1). So, the total output at time t = 1 is (f(0) * g(1)) + (f(1) * g(0)). At time t = 2, the situation gets even more complicated, with f(2) entering the picture, and f(0) and f(1) continuing to generate their responses. The total output at time t = 2 is (f(0) * g(2)) + (f(1) * g(1)) + (f(2) * g(0)). In this way, the response function effectively gets flipped in time, with τ = 0 always interacting with whatever is currently entering the black box, and the tail of the response function interacting with whatever came before.

Figure 8-8 illustrates the quantities at play at each time step (note that we’ve made time discrete for convenience of description—in reality, time is continuous, so the summation is really an integral). When computing the value of the convolution at a particular time step, you multiply the overlapping signals together and sum them.

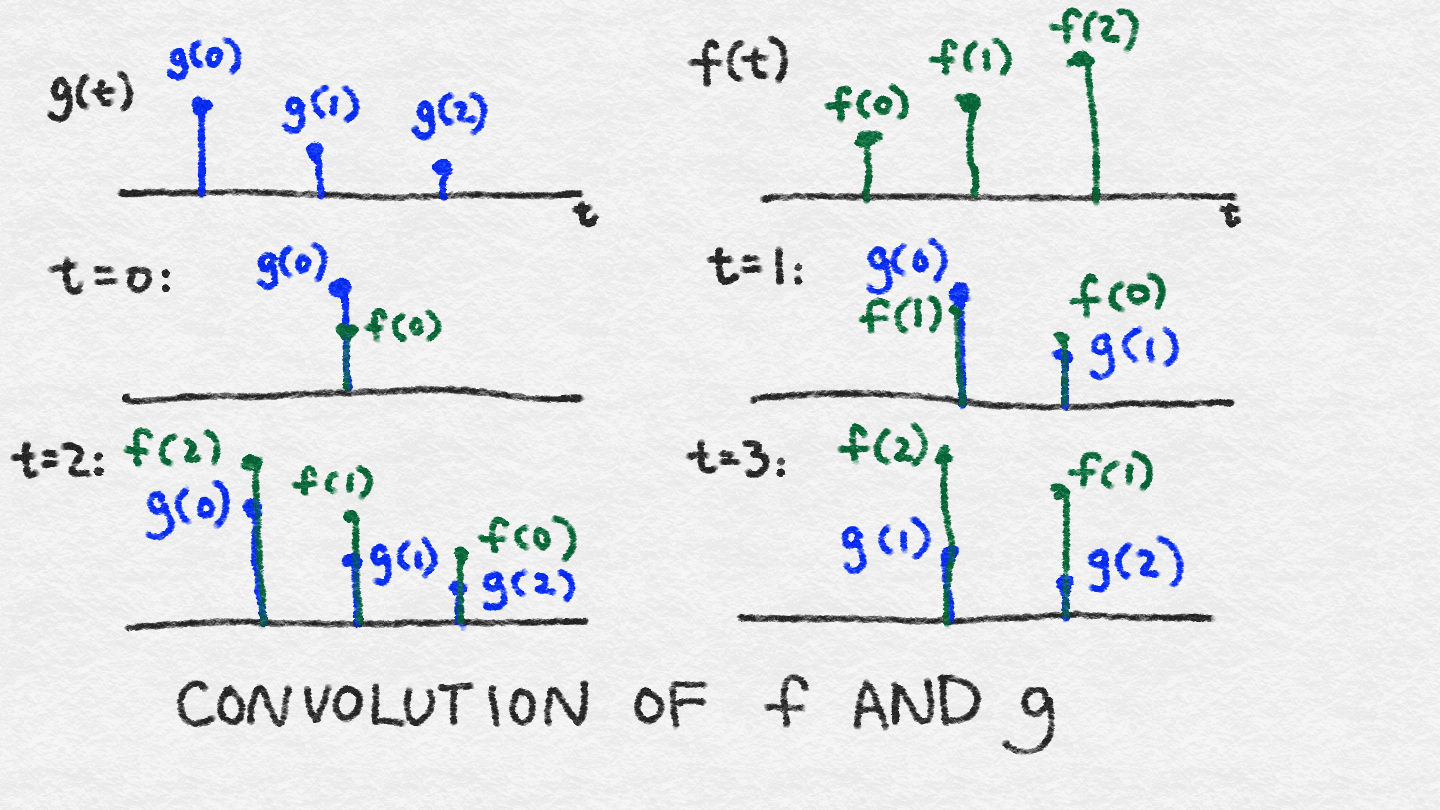
Figure 8-8. Convolution of two discrete signals, f and g

This black box is called a linear system because it doesn’t do anything more crazy than scalar multiplication and summation. The convolution operator cleanly captures the effect of a linear system.

In our example, g(t) is used to denote the response function, and f(t) the input. But since convolution is symmetric, it doesn’t really matter which is the response and which the input. The output is simply a combination of both. g(t) is also known as a filter.¹

Images are two-dimensional signals, so we need a 2D filter. A 2D convolutional filter extends the 1D case by taking the integral over two variables:

Since digital images have discrete pixels, the convolution integrals become discrete sums. Furthermore, since the number of pixels is finite, the filter function only needs a finite number of elements. In image processing, a 2D convolutional filter is also known as a kernel or a mask.

When applying a convolutional filter to an image, one does not necessarily define a giant filter that covers the entire image. Rather, one formulates a small filter covering just a few pixels by a few pixels and applies the same filter across the image, shifting over the horizontal and vertical pixel directions (see Figure 8-9).

Figure 8-9. Structure of a 1D convolutional neural net

Because the same filter is used across the image, one only needs to define a small set of parameters. The trade-off is that the filter can absorb information only within a small pixel neighborhood at a time. In other words, a convolutional neural net identifies local patterns instead of global ones.

The convolutional layers in AlexNet are three-dimensional. In other words they operate on voxels (values in the array representing the 3D space of the image) from the previous layer. The first convolutional neural net takes raw RGB images and learns convolution filters for a local image neighborhood across all three color channels. Subsequent layers take as input voxels across space and kernel dimensions. See Figure 8-14 for more details.

Rectified Linear Unit (ReLU) Transformation

The output of a neural net is often passed through another nonlinear transformation, also known as an activation function. Common choices are the tanh function (a smooth nonlinear function bounded between –1 and 1), the sigmoid function (a smooth nonlinear function bounded between 0 and 1, introduced in “Classification with Logistic Regression”), or what’s known as a rectified linear unit. A ReLU is a simple variation of a linear function where the negative part is zeroed out. In other words, it trims away the negative values, but leaves the positive part unbounded. The range of ReLU extends from 0 to ∞.

The ReLU transformation has no effect on nonnegative functions such as the raw image or the Gaussian filter. However, a trained neural net, whether fully connected or convolutional, will likely output negative values. AlexNet uses ReLU instead of other transformations, citing faster convergence during training (Krizhevsky et al., 2012). It applies ReLU to every convolutional and fully connected layer.

Response Normalization Layers

After the discussions in Chapter 4 and earlier in this chapter, normalization should by now be a familiar concept. Normalization divides an individual output by a function of the collective total response. Hence, another way of understanding normalization is that it creates competition amongst neighbors because the strength of each output is now measured relative to its neighbors (see Figure 8-12). AlexNet normalizes the output at each location across different kernels.

Figure 8-12. Structure of response normalization over convolution kernel outputs from the previous layer—the normalization constants are computed based on a neighborhood from the previous layer

Structure of AlexNet

All together, AlexNet involves five convolution layers, two response normalization layers, three max pooling layers, and two fully connected layers. Combined with the final classification output layer, there are a total of 13 neural network layers in the model, forming 8 layer groups. See Figure 8-14 for details.

Figure 8-14. Architecture diagram of AlexNet—the different shades of gray (or magenta and blue, if you’re viewing the illustrations in color) denote layers that reside on GPU 1 and GPU 2

The input image is first scaled to 256 × 256 pixels. The input is actually random crops of size 224 × 224, with 3 color channels. The first two convolution layers are each followed by a response normalization layer and a max pooling layer, and the last convolution layer is followed by max pooling. The original paper splits training data and computation across two GPUs. Communications between layers are mostly limited to within the same GPU. The exceptions are between layer groups 2 and 3, and after layer group 5. At those boundary points, the next layer takes as input a voxel of kernels from the previous layer across both GPUs. ReLU transformation follows every intermediate layer.

Figure 8-15 shows a detailed view of convolution+response normalization+max pooling. Note that the normalization constant is computed across kernels, whereas pooling happens across image regions. Also, pooling reduces the dimension of the layer.

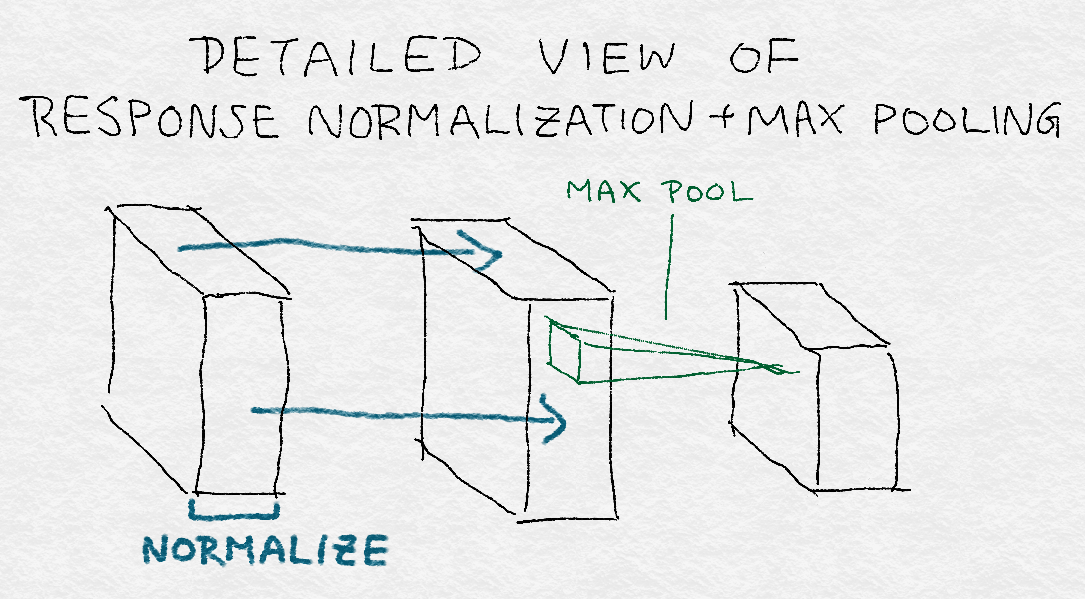
Figure 8-15. Detailed view of convolution+response normalization+max pooling

Note that AlexNet’s architecture is reminiscent of the gradient histogram–normalize–threshold–normalize architecture of SIFT/HOG feature extractors (see Figure 8-6), but with many more layers. (Hence the “deep” in “deep learning.”) Unlike in SIFT/HOG, however, the convolution kernels and full connection weights are learned from data, not predefined. Also, the normalization steps in SIFT are performed across the feature vector over the entire image region, whereas the response normalization layer in AlexNet normalizes across the convolution kernels.

At a high level, the model starts by extracting patterns out of local image neighborhoods. Each subsequent layer builds upon the output of the previous layers, effectively covering successively larger areas of the original image. Hence, even though the first five convolution layers all have fairly small kernel widths, the later layers are able to formulate more global patterns. The fully connected layers at the end are the most global.

Although the gist of patterns is conceptually clear, it is a hard problem to visualize the actual patterns each layer picks out. Figures 8-16 and 8-17 show visualizations of the first two layers of convolution kernels learned by the model. The first layer consists of detectors of grayscale edges and textures at different orientations, and color blobs and textures. The second layer appears to contain detectors of various smooth patterns.

Figure 8-16. Visualization of the first layer of convolution kernels in a trained AlexNet: the first half of the kernels are learned on GPU 1 and appear to detect grayscale edges and textures at different orientations; the second half, trained on a second GPU, focus on color blobs and patterns

Figure 8-17. Visualization of the second layer of convolution kernels of a trained AlexNet

Despite huge advances in the area, image featurization is still more of an art than a science. Ten years ago, people handcrafted feature extraction steps using a combination of image gradients, edge detection, orientation, spatial cues, smoothing, and normalization. Nowadays, deep learning architects build models that encapsulate much the same ideas, but the parameters are automatically learned from training images. The magic voodoo is still there, just hidden one abstraction deeper in the model!