Chapter 3. Text Data: Flattening, Filtering, and Chunking
What would you do if you were designing an algorithm to analyze the following paragraph of text?
Emma knocked on the door. No answer. She knocked again and waited. There was a large maple tree next to the house. Emma looked up the tree and saw a giant raven perched at the treetop. Under the afternoon sun, the raven gleamed magnificently. Its beak was hard and pointed, its claws sharp and strong. It looked regal and imposing. It reigned the tree it stood on. The raven was looking straight at Emma with its beady black eyes. Emma felt slightly intimidated. She took a step back from the door and tentatively said, “Hello?”
The paragraph contains a lot of information. We know that it involves someone named Emma and a raven. There is a house and a tree, and Emma is trying to get into the house but sees the raven instead. The raven is magnificent and has noticed Emma, who is a little scared but is making an attempt at communication.
So, which parts of this trove of information are salient features that we should extract? To start with, it seems like a good idea to extract the names of the main characters, Emma and the raven. Next, it might also be good to note the setting of a house, a door, and a tree. And what about the descriptions of the raven? What about Emma’s actions—knocking on the door, taking a step back, and saying hello?
This chapter introduces the basics of feature engineering for text. We start out with bag-of-words, which is the simplest representation based on word count statistics. A very much related transformation is tf-idf, which is essentially a feature scaling technique. It is pulled out into its own chapter (the next one) for a full discussion. The current chapter first talks about text extraction features, then delves into how to filter and clean those features.
Bag-of-X: Turning Natural Text into Flat Vectors
Whether constructing machine learning models or engineering features, it’s nice when the result is simple and interpretable. Simple things are easy to try, and interpretable features and models are easier to debug than complex ones. Simple and interpretable features do not always lead to the most accurate model, but it’s a good idea to start simple and only add complexity when absolutely necessary.
For text data, we can start with a list of word count statistics called a bag-of-words. A list of word counts makes no special effort to find the interesting entities, such as Emma or the raven. But those two words are repeatedly mentioned in our sample paragraph, and they have a higher count than a random word like “hello.” For simple tasks such as classifying a document, word count statistics often suffice. This technique can also be used in information retrieval, where the goal is to retrieve the set of documents that are relevant to an input text query. Both tasks are well served by word-level features because the presence or absence of certain words is a great indicator of the topic content of the document.
Bag-of-Words
In bag-of-words (BoW) featurization, a text document is converted into a vector of counts. (A vector is just a collection of n numbers.) The vector contains an entry for every possible word in the vocabulary. If the word—say, “aardvark”—appears three times in the document, then the feature vector has a count of 3 in the position corresponding to that word. If a word in the vocabulary doesn’t appear in the document, then it gets a count of 0. For example, the text “it is a puppy and it is extremely cute” has the BoW representation shown in Figure 3-1.

Figure 3-1. Turning raw text into a bag-of-words representation
Bag-of-words converts a text document into a flat vector. It is “flat” because it doesn’t contain any of the original textual structures. The original text is a sequence of words. But a bag-of-words has no sequence; it just remembers how many times each word appears in the text. Thus, as Figure 3-2 demonstrates, the ordering of words in the vector is not important, as long as it is consistent for all documents in the dataset. Neither does bag-of-words represent any concept of word hierarchy. For example, the concept of “animal” includes “dog,” “cat,” “raven,” etc. But in a bag-of-words representation, these words are all equal elements of the vector.

Figure 3-2. Two equivalent BoW vectors
What is important here is the geometry of data in feature space. In a bag-of-words vector, each word becomes a dimension of the vector. If there are n words in the vocabulary, then a document becomes a point1 in n-dimensional space. It is difficult to visualize the geometry of anything beyond two or three dimensions, so we will have to use our imagination. Figure 3-3 shows what our example sentence looks like in the two-dimensional feature space corresponding to the words “puppy” and “cute.”
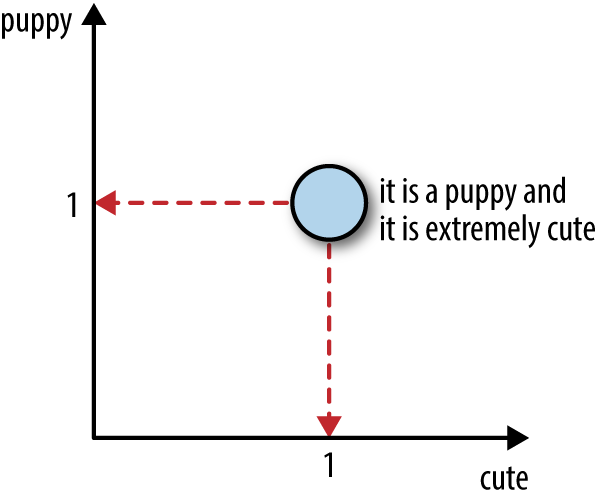
Figure 3-3. Illustration of a sample text document in a 2D feature space
Figure 3-4 shows three sentences in a 3D space corresponding to the words “puppy,” “extremely,” and “cute.”

Figure 3-4. Three sentences in 3D feature space
These figures both depict data vectors in feature space. The axes denote individual words, which are features in the bag-of-words representation, and the points in space denote data points (text documents). Sometimes it is also informative to look at feature vectors in data space. A feature vector contains the value of the feature in each data point. The axes denote individual data points, and the points denote feature vectors. Figure 3-5 shows an example. With bag-of-words featurization for text documents, a feature is a word, and a feature vector contains the counts of this word in each document. In this way, a word is represented as a “bag-of-documents.” As we shall see in Chapter 4, these bag-of-documents vectors come from the matrix transpose of the bag-of-words vectors.

Figure 3-5. Word vectors in document space
Bag-of-words is not perfect. Breaking down a sentence into single words can destroy the semantic meaning. For instance, “not bad” semantically means “decent” or even “good” (especially if you’re British). But “not” and “bad” constitute a floating negation plus a negative sentiment. “toy dog” and “dog toy” could be very different things (unless it’s a dog toy of a toy dog), and the meaning is lost with the singleton words “toy” and “dog.” It’s easy to come up with many such examples. Bag-of-n-Grams, which we discuss next, alleviates some of the issue but is not a fundamental fix. It’s good to keep in mind that bag-of-words is a simple and useful heuristic, but it is far from a correct semantic understanding of text.
Bag-of-n-Grams
Bag-of-n-Grams, or bag-of-n-grams, is a natural extension of bag-of-words. An n-gram is a sequence of n tokens. A word is essentially a 1-gram, also known as a unigram. After tokenization, the counting mechanism can collate individual tokens into word counts, or count overlapping sequences as n-grams. For example, the sentence “Emma knocked on the door” generates the n-grams “Emma knocked,” “knocked on,” “on the,” and “the door.”
n-grams retain more of the original sequence structure of the text, and therefore the bag-of-n-grams representation can be more informative. However, this comes at a cost. Theoretically, with k unique words, there could be k2 unique 2-grams (also called bigrams). In practice, there are not nearly so many, because not every word can follow every other word. Nevertheless, there are usually a lot more distinct n-grams (n > 1) than words. This means that bag-of-n-grams is a much bigger and sparser feature space. It also means that n-grams are more expensive to compute, store, and model. The larger n is, the richer the information, and the greater the cost.
To illustrate how the number of n-grams grows with increasing n (see Figure 3-6), let’s compute n-grams on the Yelp reviews dataset. In Example 3-1, we compute the n-grams of the first 10,000 reviews using Pandas and the CountVectorizer transformer in scikit-learn.
Example 3-1. Computing n-grams
>>>importpandas>>>importjson>>>fromsklearn.feature_extraction.textimportCountVectorizer# Load the first 10,000 reviews>>>f=open('data/yelp/v6/yelp_academic_dataset_review.json')>>>js=[]>>>foriinrange(10000):...js.append(json.loads(f.readline()))>>>f.close()>>>review_df=pd.DataFrame(js)# Create feature transformers for unigrams, bigrams, and trigrams.# The default ignores single-character words, which is useful in practice because# it trims uninformative words, but we explicitly include them in this example for# illustration purposes.>>>bow_converter=CountVectorizer(token_pattern='(?u)\b\w+\b')>>>bigram_converter=CountVectorizer(ngram_range=(2,2),...token_pattern='(?u)\b\w+\b')>>>trigram_converter=CountVectorizer(ngram_range=(3,3),...token_pattern='(?u)\b\w+\b')# Fit the transformers and look at vocabulary size>>>bow_converter.fit(review_df['text'])>>>words=bow_converter.get_feature_names()>>>bigram_converter.fit(review_df['text'])>>>bigrams=bigram_converter.get_feature_names()>>>trigram_converter.fit(review_df['text'])>>>trigrams=trigram_converter.get_feature_names()>>>(len(words),len(bigrams),len(trigrams))26047 346301 847545# Sneak a peek at the n-grams themselves>>>words[:10]['0', '00', '000', '0002', '00am', '00ish', '00pm', '01', '01am', '02']>>>bigrams[-10:]['zucchinis at','zucchinis took','zucchinis we','zuma over','zuppa di','zuppa toscana','zuppe di','zurich and','zz top','à la']>>>trigrams[:10]['0 10 definitely','0 2 also','0 25 per','0 3 miles','0 30 a','0 30 everything','0 30 lb','0 35 tip','0 5 curry','0 5 pork']

Figure 3-6. Number of unique n-grams in the first 10,000 reviews of the Yelp dataset
Filtering for Cleaner Features
With words, how do we cleanly separate the signal from the noise? Through filtering, techniques that use raw tokenization and counting to generate lists of simple words or n-grams become more usable. Phrase detection, which we will discuss next, can be seen as a particular bigram filter. Here are a few more ways to perform filtering.
Stopwords
Classification and retrieval do not usually require an in-depth understanding of the text. For instance, in the sentence “Emma knocked on the door,” the words “on” and “the” don’t change the fact that this sentence is about a person and a door. For coarse-grained tasks such as classification, the pronouns, articles, and prepositions may not add much value. The case may be very different in sentiment analysis, which requires a fine-grained understanding of semantics.
The popular Python NLP package NLTK contains a linguist-defined stopword list for many languages. (You will need to install NLTK and run nltk.download() to get all the goodies.) Various stopword lists can also be found on the web. For instance, here are some sample words from the English stopword list:
a, about, above, am, an, been, didn't, couldn't, i'd, i'll, itself, let's, myself, our, they, through, when's, whom, ...
Note that the list contains apostrophes, and the words are uncapitalized. In order to use it as is, the tokenization process must not eat up apostrophes, and the words need to be converted to lowercase.
Frequency-Based Filtering
Stopword lists are a way of weeding out common words that make for vacuous features. There are other, more statistical ways of getting at the concept of “common words.” In collocation extraction, we see methods that depend on manual definitions, and those that use statistics. The same idea applies to word filtering. We can use frequency statistics here as well.
Frequent words
Frequency statistics are great for filtering out corpus-specific common words as well as general-purpose stopwords. For instance, the phrase “New York Times” and each of the individual words in it appear frequently in the New York Times Annotated Corpus dataset. Similarly, the word “house” appears often in the phrase “House of Commons” in the Hansard corpus of Canadian parliament debates, a dataset that is popularly used for statistical machine translation because it contains both an English and a French version of all documents. These words are meaningful in general, but not within those particular corpora. A typical stopword list will catch the general stopwords, but not corpus-specific ones.
Looking at the most frequent words can reveal parsing problems and highlight normally useful words that happen to appear too many times in the corpus. For example, Table 3-1 lists the 40 most frequent words in the Yelp reviews dataset. Here, frequency is based on the number of documents (reviews) they appear in, not their count within a document. As we can see, the list includes many stopwords. It also contains some surprises. “s” and “t” are on the list because we used the apostrophe as a tokenization delimiter, and words such as “Mary’s” or “didn’t” got parsed as “Mary s” and “didn t.” Furthermore, the words “good,” “food,” and “great” each appear in around a third of the reviews, but we might want to keep them around because they are very useful for tasks such as sentiment analysis or business categorization.
| Rank | Word | Document frequency | Rank | Word | Document frequency |
|---|---|---|---|---|---|
| 1 | the | 1416058 | 21 | t | 684049 |
| 2 | and | 1381324 | 22 | not | 649824 |
| 3 | a | 1263126 | 23 | s | 626764 |
| 4 | i | 1230214 | 24 | had | 620284 |
| 5 | to | 1196238 | 25 | so | 608061 |
| 6 | it | 1027835 | 26 | place | 601918 |
| 7 | of | 1025638 | 27 | good | 598393 |
| 8 | for | 993430 | 28 | at | 596317 |
| 9 | is | 988547 | 29 | are | 585548 |
| 10 | in | 961518 | 30 | food | 562332 |
| 11 | was | 929703 | 31 | be | 543588 |
| 12 | this | 844824 | 32 | we | 537133 |
| 13 | but | 822313 | 33 | great | 520634 |
| 14 | my | 786595 | 34 | were | 516685 |
| 15 | that | 777045 | 35 | there | 510897 |
| 16 | with | 775044 | 36 | here | 481542 |
| 17 | on | 735419 | 37 | all | 478490 |
| 18 | they | 720994 | 38 | if | 475175 |
| 19 | you | 701015 | 39 | very | 460796 |
| 20 | have | 692749 | 40 | out | 460452 |
In practice, it helps to combine frequency-based filtering with a stopword list. There is also the tricky question of where to place the cutoff. Unfortunately there is no universal answer. Most of the time the cutoff needs to be determined manually, and may need to be reexamined when the dataset changes.
Rare words
Depending on the task, one might also need to filter out rare words. These might be truly obscure words, or misspellings of common words. To a statistical model, a word that appears in only one or two documents is more like noise than useful information. For example, suppose the task is to categorize businesses based on their Yelp reviews, and a single review contains the word “gobbledygook.” How would one tell, based on this one word, whether the business is a restaurant, a beauty salon, or a bar? Even if we knew that the business in this case happened to be a bar, it would probably be a mistake to classify as such for other reviews that contain the word “gobbledygook.”
Not only are rare words unreliable as predictors, they also generate computational overhead. The set of 1.6 million Yelp reviews contains 357,481 unique words (tokenized by space and punctuation characters), 189,915 of which appear in only one review, and 41,162 in two reviews. Over 60% of the vocabulary occurs rarely. This is a so-called heavy-tailed distribution, and it is very common in real-world data. The training time of many statistical machine learning models scales linearly with the number of features, and some models are quadratic or worse. Rare words incur a large computation and storage cost for not much additional gain.
Rare words can be easily identified and trimmed based on word count statistics. Alternatively, their counts can be aggregated into a special garbage bin, which can serve as an additional feature. Figure 3-7 demonstrates this representation on a short document that contains a bunch of usual words and two rare words, “gobbledygook” and “zylophant.” The usual words retain their own counts, which can be further filtered by stopword lists or other frequency-based methods. The rare words lose their identity and get grouped into a garbage bin feature.

Figure 3-7. Bag-of-words feature vector with a garbage bin
Since one won’t know which words are rare until the whole corpus has been counted, the garbage bin feature will need to be collected as a post-processing step.
Since this book is about feature engineering, our focus is on features. But the concept of rarity also applies to data points. If a text document is very short, then it likely contains no useful information and should not be used when training a model. One must use caution when applying this rule, however. The Wikipedia dump contains many pages that are incomplete stubs, which are probably safe to filter out. Tweets, on the other hand, are inherently short, and require other featurization and modeling tricks.
Stemming
One problem with simple parsing is that different variations of the same word get counted as separate words. For instance, “flower” and “flowers” are technically different tokens, and so are “swimmer,” “swimming,” and “swim,” even though they are very close in meaning. It would be nice if all of these different variations got mapped to the same word.
Stemming is an NLP task that tries to chop each word down to its basic linguistic word stem form. There are different approaches. Some are based on linguistic rules, others on observed statistics. A subclass of algorithms incorporate part-of-speech tagging and linguistic rules in a process known as lemmatization.
Most stemming tools focus on the English language, though efforts are ongoing for other languages. The Porter stemmer is the most widely used free stemming tool for the English language. The original program is written in ANSI C, but many other packages have since wrapped it to provide access to other languages.
Here is an example of running the Porter stemmer through the NLTK Python package. As you can see, it handles a large number of cases, but it’s not perfect. The word “goes” is mapped to “goe,” while “go” is mapped to itself:
>>>importnltk>>>stemmer=nltk.stem.porter.PorterStemmer()>>>stemmer.stem('flowers')u'flower'>>>stemmer.stem('zeroes')u'zero'>>>stemmer.stem('stemmer')u'stem'>>>stemmer.stem('sixties')u'sixti'>>>stemmer.stem('sixty')u'sixty'>>>stemmer.stem('goes')u'goe'>>>stemmer.stem('go')u'go'
Stemming does have a computation cost. Whether the end benefit outweighs the cost is application-dependent. It is also worth noting that stemming could hurt more than it helps. The words “new” and “news” have very different meanings, but both would be stemmed to “new.” Similar examples abound. For this reason, stemming is not always used.
Atoms of Meaning: From Words to n-Grams to Phrases
The concept of bag-of-words is straightforward. But how does a computer know what a word is? A text document is represented digitally as a string, which is basically a sequence of characters. One might also run into semi-structured text in the form of JSON blobs or HTML pages. But even with the added tags and structure, the basic unit is still a string. How does one turn a string into a sequence of words? This involves the tasks of parsing and tokenization, which we discuss next.
Parsing and Tokenization
Parsing is necessary when the string contains more than plain text. For instance, if the raw data is a web page, an email, or a log of some sort, then it contains additional structure. One needs to decide how to handle the markup, the headers and footers, or the uninteresting sections of the log. If the document is a web page, then the parser needs to handle URLs. If it is an email, then fields like From, To, and Subject may require special handling—otherwise these headers will end up as normal words in the final count, which may not be useful.
After light parsing, the plain-text portion of the document can go through tokenization. This turns the string—a sequence of characters—into a sequence of tokens. Each token can then be counted as a word. The tokenizer needs to know what characters indicate that one token has ended and another is beginning. Space characters are usually good separators, as are punctuation characters. If the text contains tweets, then hash marks (#) should not be used as separators (also known as delimiters).
Sometimes, the analysis needs to operate on sentences instead of entire documents. For instance, n-grams, a generalization of the concept of a word, should not extend beyond sentence boundaries. More complex text featurization methods like word2vec also work with sentences or paragraphs. In these cases, one needs to first parse the document into sentences, then further tokenize each sentence into words.
String Objects: More Than Meets the Eye
String objects come in various encodings, like ASCII or Unicode. Plain English text can be encoded in ASCII. Most other languages require Unicode. If the document contains non-ASCII characters, then make sure that the tokenizer can handle that particular encoding. Otherwise, the results will be incorrect.
Collocation Extraction for Phrase Detection
A sequence of tokens immediately yields the list of words and n-grams. Semantically speaking, however, we are more used to understanding phrases, not n-grams. In computational natural language processing (NLP), the concept of a useful phrase is called a collocation. In the words of Manning and Schütze (1999: 151), “A collocation is an expression consisting of two or more words that correspond to some conventional way of saying things.”
Collocations are more meaningful than the sum of their parts. For instance, “strong tea” has a different meaning beyond “great physical strength” and “tea”; therefore, it is considered a collocation. The phrase “cute puppy,” on the other hand, means exactly the sum of its parts: “cute” and “puppy.” Thus, it is not considered a collocation.
Collocations do not have to be consecutive sequences. For example, the sentence “Emma knocked on the door” is considered to contain the collocation “knock door.” Hence, not every collocation is an n-gram. Conversely, not every n-gram is deemed a meaningful collocation.
Because collocations are more than the sum of their parts, their meaning cannot be adequately captured by individual word counts. Bag-of-words falls short as a representation. Bag-of-n-grams is also problematic because it captures too many meaningless sequences (consider “this is” in the bag-of-n-grams example) and not enough of the meaningful ones (i.e., knock door).
Collocations are useful as features. But how does one discover and extract them from text? One way is to predefine them. If we tried really hard, we could probably find comprehensive lists of idioms in various languages, and we could look through the text for any matches. It would be very expensive, but it would work. If the corpus is very domain specific and contains esoteric lingo, then this might be the preferred method. But the list would require a lot of manual curation, and it would need to be constantly updated for evolving corpora. For example, it probably wouldn’t be very realistic for analyzing tweets, or for blogs and articles.
Since the advent of statistical NLP in the last two decades, people have opted more and more for statistical methods for finding phrases. Instead of establishing a fixed list of phrases and idiomatic sayings, statistical collocation extraction methods rely on the ever-evolving data to reveal the popular sayings of the day.
Frequency-based methods
A simple hack is to look at the most frequently occurring n-grams. The problem with this approach is that the most frequently occurring ones may not be the most useful ones. Table 3-2 shows the most popular bigrams () in the entire Yelp reviews dataset. As we can see, the top 10 most frequently occurring bigrams by document count are very generic terms that don’t contain much meaning.
| Bigram | Document count |
|---|---|
| of the | 450,849 |
| and the | 426,346 |
| in the | 397,821 |
| it was | 396,713 |
| this place | 344,800 |
| it s | 341,090 |
| and i | 332,415 |
| on the | 325,044 |
| i was | 285,012 |
| for the | 276,946 |
Hypothesis testing for collocation extraction
Raw popularity count is too crude of a measure. We have to find more clever statistics to be able to pick out meaningful phrases easily. The key idea is to ask whether two words appear together more often than they would by chance. The statistical machinery for answering this question is called a hypothesis test.
Hypothesis testing is a way to boil noisy data down to “yes” or “no” answers. It involves modeling the data as samples drawn from random distributions. The randomness means that one can never be 100% sure about the answer; there’s always the chance of an outlier. So, the answers are attached to a probability.
For example, the outcome of a hypothesis test might be “these two datasets come from the same distribution with 95% probability.” For a gentle introduction to hypothesis testing, see the Khan Academy’s tutorial on Hypothesis Testing and p-Values.
In the context of collocation extraction, many hypothesis tests have been proposed over the years. One of the most successful methods is based on the likelihood ratio test (Dunning, 1993). For a given pair of words, the method tests two hypotheses on the observed dataset. Hypothesis 1 (the null hypothesis) says that word 1 appears independently from word 2. Another way of saying this is that seeing word 1 has no bearing on whether we also see word 2. Hypothesis 2 (the alternate hypothesis) says that seeing word 1 changes the likelihood of seeing word 2. We take the alternate hypothesis to imply that the two words form a common phrase. Hence, the likelihood ratio test for phrase detection (a.k.a. collocation extraction) asks the following question: are the observed word occurrences in a given text corpus more likely to have been generated from a model where the two words occur independently from one another, or a model where the probabilities of the two words are entangled?
That is a mouthful. Let’s math it up a little. (Math is great at expressing things very precisely and concisely, but it does require a completely different parser than natural language.)
We can express the null hypothesis Hnull (independent) as P(w2 | w1) = P(w2 | not w1), and the alternate hypothesis Halternate (not independent) as P(w2 | w1) ≠ P(w2 | not w1).
The final statistic is the log of the ratio between the two:
The likelihood function L(Data; H) represents the probability of seeing the word frequencies in the dataset under the independent or the not independent model for the word pair. In order to compute this probability, we have to make another assumption about how the data is generated. The simplest data generation model is the binomial model, where for each word in the dataset, we toss a coin, and we insert our special word if the coin comes up heads, and some other word otherwise. Under this strategy, the count of the number of occurrences of the special word follows a binomial distribution. The binomial distribution is completely determined by the total number of words, the number of occurrences of the word of interest, and the heads probability.
The algorithm for detecting common phrases through likelihood ratio test analysis proceeds as follows:
- Compute occurrence probabilities for all singleton words: P(w).
- Compute conditional pairwise word occurrence probabilities for all unique bigrams: P(w2 | w1).
- Compute the likelihood ratio log λ for all unique bigrams.
- Sort the bigrams based on their likelihood ratio.
- Take the bigrams with the smallest likelihood ratio values as features.
Getting a Grip on the Likelihood Ratio Test
The key is that what the test compares is not the probability parameters themselves, but rather the probability of seeing the observed data under those parameters (and an assumed data generation model). Likelihood is one of the key principles of statistical learning, but it is definitely a brain-twister the first few times you see it. Once you work out the logic, it becomes intuitive.
There is another statistical approach that’s based on pointwise mutual information, but it is very sensitive to rare words, which are always present in real-world text corpora. Hence, it is not commonly used and we will not be demonstrating it here.
Note that all of the statistical methods for collocation extraction, whether using raw frequency, hypothesis testing, or pointwise mutual information, operate by filtering a list of candidate phrases. The easiest and cheapest way to generate such a list is by counting n-grams. It’s possible to generate nonconsecutive sequences, but they are expensive to compute. In practice, even for consecutive n-grams, people rarely go beyond bigrams or trigrams because there are too many of them, even after filtering. To generate longer phrases, there are other methods such as chunking or combining with part-of-speech (PoS) tagging.
Chunking and part-of-speech tagging
Chunking is a bit more sophisticated than finding n-grams, in that it forms sequences of tokens based on parts of speech, using rule-based models.
For example, we might be most interested in finding all of the noun phrases in a problem where the entity (in this case the subject of a text) is the most interesting to us. In order to find this, we tokenize each word with a part of speech and then examine the token’s neighborhood to look for part-of-speech groupings, or “chunks.” The models that map words to parts of speech are generally language specific. Several open source Python libraries, such as NLTK, spaCy, and TextBlob, have multiple language models available.
To illustrate how several libraries in Python make chunking using PoS tagging fairly straightforward, let’s use the Yelp reviews dataset again. In Example 3-2, we evaluate the parts of speech to find the noun phrases using both spaCy and TextBlob.
Example 3-2. PoS tagging and chunking
>>>importpandasaspd>>>importjson# Load the first 10 reviews>>>f=open('data/yelp/v6/yelp_academic_dataset_review.json')>>>js=[]>>>foriinrange(10):...js.append(json.loads(f.readline()))>>>f.close()>>>review_df=pd.DataFrame(js)# First we'll walk through spaCy's functions>>>importspacy# preload the language model>>>nlp=spacy.load('en')# We can create a Pandas Series of spaCy nlp variables>>>doc_df=review_df['text'].apply(nlp)# spaCy gives us fine-grained parts of speech using (.pos_)# and coarse-grained parts of speech using (.tag_)>>>fordocindoc_df[4]:...([doc.text,doc.pos_,doc.tag_])Got VERB VBPa DET DTletter NOUN NNin ADP INthe DET DTmail NOUN NNlast ADJ JJweek NOUN NNthat ADJ WDTsaid VERB VBDDr. PROPN NNPGoldberg PROPN NNPis VERB VBZmoving VERB VBGto ADP INArizona PROPN NNPto PART TOtake VERB VBa DET DTnew ADJ JJposition NOUN NNthere ADV RBin ADP INJune PROPN NNP. PUNCT .SPACE SPHe PRON PRPwill VERB MDbe VERB VBmissed VERB VBNvery ADV RBmuch ADV RB. PUNCT .SPACE SPI PRON PRPthink VERB VBPfinding VERB VBGa DET DTnew ADJ JJdoctor NOUN NNin ADP INNYC PROPN NNPthat ADP INyou PRON PRPactually ADV RBlike INTJ UHmight VERB MDalmost ADV RBbe VERB VBas ADV RBawful ADJ JJas ADP INtrying VERB VBGto PART TOfind VERB VBa DET DTdate NOUN NN! PUNCT .# spaCy also does some basic noun chunking for us>>>([chunkforchunkindoc_df[4].noun_chunks])[a letter, the mail, Dr. Goldberg, Arizona, a new position, June, He, I,a new doctor, NYC, you, a date]###### We can do the same feature transformations using Textblobfrom textblob import TextBlob# The default tagger in TextBlob uses the PatternTagger, which is OK for our example.# You can also specify the NLTK tagger, which works better for incomplete sentences.>>>blob_df=review_df['text'].apply(TextBlob)>>>blob_df[4].tags[('Got', 'NNP'),('a', 'DT'),('letter', 'NN'),('in', 'IN'),('the', 'DT'),('mail', 'NN'),('last', 'JJ'),('week', 'NN'),('that', 'WDT'),('said', 'VBD'),('Dr.', 'NNP'),('Goldberg', 'NNP'),('is', 'VBZ'),('moving', 'VBG'),('to', 'TO'),('Arizona', 'NNP'),('to', 'TO'),('take', 'VB'),('a', 'DT'),('new', 'JJ'),('position', 'NN'),('there', 'RB'),('in', 'IN'),('June', 'NNP'),('He', 'PRP'),('will', 'MD'),('be', 'VB'),('missed', 'VBN'),('very', 'RB'),('much', 'JJ'),('I', 'PRP'),('think', 'VBP'),('finding', 'VBG'),('a', 'DT'),('new', 'JJ'),('doctor', 'NN'),('in', 'IN'),('NYC', 'NNP'),('that', 'IN'),('you', 'PRP'),('actually', 'RB'),('like', 'IN'),('might', 'MD'),('almost', 'RB'),('be', 'VB'),('as', 'RB'),('awful', 'JJ'),('as', 'IN'),('trying', 'VBG'),('to', 'TO'),('find', 'VB'),('a', 'DT'),('date', 'NN')]>>>([npfornpinblob_df[4].noun_phrases])['got', 'goldberg', 'arizona', 'new position', 'june', 'new doctor', 'nyc']
You can see that the noun phrases found by each library are a little bit different. spaCy includes common words in the English language like “a” and “the,” while TextBlob removes these. This reflects a difference in the rules engines that drive what each library considers to be a noun phrase. You can also write your part-of-speech relationships to define the chunks you are seeking. See Bird et al. (2009) to really dive deep into chunking with Python from scratch.
Summary
The bag-of-words representation is simple to understand, easy to compute, and useful for classification and search tasks. But sometimes single words are too simplistic to encapsulate some information in the text. To fix this problem, people look to longer sequences. Bag-of-n-grams is a natural generalization of bag-of-words. The concept is still easy to understand, and it’s just as easy to compute as bag-of-words.
Bag-of-n-grams generates a lot more distinct n-grams. It increases the feature storage cost, as well as the computation cost of the model training and prediction stages. The number of data points remains the same, but the dimension of the feature space is now much larger. Hence, the data is much more sparse. The higher n is, the higher the storage and computation cost, and the sparser the data. For these reasons, longer n-grams do not always lead to improvements in model accuracy (or any other performance measure). People usually stop at n = 2 or 3. Longer n-grams are rarely used.
One way to combat the increase in sparsity and cost is to filter the n-grams and retain only the most meaningful phrases. This is the goal of collocation extraction. In theory, collocations (or phrases) could form nonconsecutive token sequences in the text. In practice, however, looking for nonconsecutive phrases has a much higher computation cost for not much gain. So, collocation extraction usually starts with a candidate list of bigrams and utilizes statistical methods to filter them.
All of these methods turn a sequence of text tokens into a disconnected set of counts. Sets have much less structure than sequences; they lead to flat feature vectors.
In this chapter, we dipped our toes into the water with simple text featurization techniques. These techniques turn a piece of natural language text—full of rich semantic structure—into a simple flat vector. We discussed a number of common filtering techniques to clean up the vector entries. We also introduced n-grams and collocation extraction as methods that add a little more structure into the flat vectors. The next chapter goes into a lot more detail about another common text featurization trick called tf-idf. Subsequent chapters will discuss more methods for adding structure back into a flat vector.
Bibliography
Bird, Steven, Ewan Klein, and Edward Loper. Natural Language Processing with Python. Sebastopol, CA: O’Reilly Media, 2009.
Dunning, Ted. “Accurate Methods for the Statistics of Surprise and Coincidence.” ACM Journal of Computational Linguistics, special issue on using large corpora 19:1 (1993): 61–74.
Khan Academy. “Hypothesis Testing and p-Values.” Retrieved from https://www.khanacademy.org/math/probability/statistics-inferential/hypothesis-testing/v/hypothesis-testing-and-p-values.
Manning, Christopher D. and Hinrich Schütze. Foundations of Statistical Natural Language Processing. Cambridge, MA: MIT Press, 1999.
1 Sometimes people use the term “document vector.” The vector extends from the origin and ends at the specified point. For our purposes, “vector” and “point” are the same thing.
