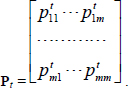11
Performance Persistence of Polish Mutual Funds: Mobility Measures
The purpose of this chapter was to evaluate the phenomenon of performance persistence in a developing market. The analysis was conducted for Polish mutual funds from three time perspectives: monthly, quarterly and yearly. The research approach applied was a Markovian framework supported with a few mobility measures. The results reveal the existence of limited performance persistence, which decreases as the timeframe increases. Moreover, the observed propensity for a relative repetition of mutual fund performance in consecutive periods seems to involve losers rather than winners, and hence it takes the form of the “icy hand” effect.
11.1. Introduction
The notion of the “hot hand” is defined in social psychology as a string of successes believed in by many gamblers during continued gaming. The name of the phenomenon originates from the conviction shared by basketball players and fans that the likelihood of a player hitting a shot is greater after a hit than after a miss on the previous shot (Wilkinson and Klaes 2012). In finance, the term stands for making decisions on the basis of an increase in stock prices in the previous period on the assumption that it will be similar in the next period (see Haslem 2003). Another cognitive social bias, the so-called “gambler’s fallacy”, is in a way an opposite concept, as it describes the situation of a mistaken belief that the occurrence of a certain random event is less expected to happen following an event or a series of events.
The hot-hand phenomenon can be extended to the literature on mutual funds, where it is better known as performance persistence, which means financial intermediaries’ tendency to achieve similar results in consecutive periods. Present studies distinguish two types of this tendency: winning persistence, which occurs when managers repeat good investment results, and its opposite – losing persistence, which means achieving bad results in subsequent periods. With respect to the subject matter of this chapter, winning persistence can be correlated with the hot-hand effect, while losing persistence can be correlated with the opposite phenomenon, namely the so-called “icy hand”.
The issue of the hot-hand or icy-hand effect in the performance of mutual funds could be highly useful to managers of collective investment companies as well as individual investors for a number of reasons. The former could apply the findings associated with these effects from behavioral finance in their information and marketing activities. The latter, in turn, might find the relations between the results occurring in consecutive periods important in the context of evaluating returns and continuing the possible winning or losing streak. Moreover, advantages of this issue can be viewed from a third perspective: studies dealing with hot-handed managers of funds enable academicians to evaluate the intensity of competition in the branch or enhance the knowledge about portfolio management theories.
The main purpose of this chapter is to examine whether the performance persistence phenomenon exists in the Polish mutual fund market. To this end, the Markovian approach, used in the construction of special chains with transition matrices, supported with a few mobility measures, can be employed. This framework is still unknown in the area of finance. Nevertheless, this study, along with the findings of Filip and Rogala (2021), may be considered as an introduction to the research on the performance of mutual funds in developing countries by means of stochastic processes and as a basis for further discussions and analyses with this respect.
The remainder of this chapter is organized as follows: section 11.2 briefly reviews the financial literature concerned with performance persistence in consecutive periods and groups the most significant studies by research methods and geographical criteria adopted by authors; section 11.3 concentrates on the empirical design and dataset; section 11.4 provides empirical findings and the final section presents the concluding remarks.
11.2. Literature review
This section will provide a brief review of the literature discussing research on performance persistence. Such research normally consists in comparing the rates of return achieved in successive periods. In some of the above-mentioned studies, performance analyses adopt an approach related to stochastic modeling, which will be emphasized in this chapter.
The analysis of the relevant literature discussing the issue of persistence of the mutual fund allocation effects has allowed identification of three groups of research. The first one covers basic research, which was the first to show performance persistence and at the same time constituted the starting point for numerous subsequent inquiries. The criterion for classifying studies to another group was the emergence of more recent streams in this area, which comprised more advanced research approaches. One of them is the publications engaging a Markov chain. The last group of research included in the review contains the studies describing the European, including Polish, experiences as regards the occurrence of performance persistence of domestic mutual funds.
The empirical studies of the turn of the 1990s (Grinblatt and Titman 1989; Brown and Goetzmann 1995) were the first to suggest a relative stability of the returns generated by mutual funds. It is then that, for example, Hendricks et al. (1993) identified the above-mentioned hot-hand effect, which refers to a short-term performance persistence. Other studies attempted also to determine whether performance persistence was connected with managerial characteristics or stock selection (e.g. Grinblatt and Titman 1992). The additionally asked question concerned the issue whether performance persistence of mutual funds might possibly be a group phenomenon of adopting a common investment strategy consisting in allocating assets to the securities that performed well in earlier periods (e.g. Goetzmann and Ibbotson 1994). This is when a set of research tools ranging from regression models and analysis of Spearman rank correlation coefficients to the now classical contingency tables were developed.
One of the reasons for the relative performance persistence over time was identified as the so-called survivorship bias. For instance, Malkiel (1995), whose inquiries additionally involved the funds which discontinued their activities, stated that the evidence for recurring results in a survivorship-bias-free sample deteriorated with time. At the same time, he was critical about the hypothesis providing that some managers were able to continuously achieve better results at an acceptable risk level. Carhart (1997), in turn, noted that funds generating better short-term returns managed to do so by applying a momentum strategy. On the other hand, returns on investments diminished after transaction costs were taken into account. Significant performance persistence was notable, but this was the case with losing funds.
In subsequent years, a few important research streams emerged in the discussed area. They were characterized by using more advanced research techniques. For instance, Huij and Verbeek (2007) showed, based on Bayesian methods, that historical results achieved by equity funds influenced future performance, yet in the short term only. When extending the timeframe of the analysis, the relations between the returns generated in successive periods vanished. Interestingly, the persistence effect of good performance was stronger for younger and smaller funds. The researchers argued that achieving higher or lower results is related to managers’ luck rather than skills.
Huij and Derwall (2008), in turn, chose to use and confront a broad range of research methods: from contingency tables, which are traditional for the discussed stream of the relevant literature, to bootstrap techniques. Their findings showed that the examined bond funds, which were characterized by good and poor performance in the past, repeated their rates of return in subsequent periods. Using traditional research methods, this study demonstrates the existence of a relationship between managerial skills and performance persistence in virtually all analyzed groups of funds.
The first studies employing the Markovian approach to the research on performance persistence were published only recently. One of them is Drakos et al. (2015), which uses Markov chains, supported with an expanded set of mobility measures, to analyze performance dependence in consecutive periods. The authors noted a certain tendency for repeating performance of mutual funds. They called it inertia, which, however, was characterized by a decrease over time. The applied mobility indices imply the increasing degree of performance reversal, which means departure from performance persistence.
Studies from non-US markets refer to the invoked research approaches relying on Markov chains fairly infrequently. The group of research from European markets that employ chiefly traditional tools includes, for example, Otten and Bams (2002). Its authors dealt with the results achieved by equity funds coming from the United Kingdom, France, Germany, Italy and the Netherlands. Earlier, however, Dahlquist et al. (2000) based their reasoning on a sample of Swedish funds operating in several core market segments. Casarin et al. (2008), in turn, examined performance persistence for Italian funds.
From among more recent studies, which, however, come from developing markets, the following also deserve attention: Koutsokostas et al. (2020) for Greek equity funds, performance assessment for Hungarian funds by Bota and Ormos (2017), studies by Czekaj and Grotowski (2014) and Machnik (2020), among others, for Polish funds. The findings of the above-mentioned analyses were not consistent, but long-term persistence was ruled out virtually every time. In the context of an attempt to capture short-term persistence, the conclusions were more convergent, yet often dependent on the employed research approach or performance measure. Generally, the relevant literature, despite the multitude of studies, the abundance of topics and the diversity of the used data, has still failed to provide straightforward answers to a number of substantial questions. This means that the discussed phenomenon deserves a further analysis.
11.3. Dataset and empirical design
The sample used in this study consists of 101 Polish open-end investment funds covering the period from January 2000 to September 2018. The dataset involving monthly unit prices of the above registered domestic equity funds was derived from the reports by Analizy Online, a web service collecting this kind of information in Poland. Moreover, data on the values of the stock exchange index, which was important for calculating the used measure of returns, came from the Warsaw Stock Exchange (GPW) website.
The performance measurement employed in this study uses asset unit values. It was decided to use continuous return as the base rate, which is one of the most popular measures of investment effects used in financial analyses. It is based on the values of funds’ share units and can be calculated logarithmically as follows:
where ri is the continuous return of fund i in period t and upt and upt-1 are the unit prices of fund i at the end (t) and at the beginning (t-1) of the analyzed period, respectively.
In the next step, the median of the rates of return calculated in this manner is used to identify the winning funds and the losing funds in individual periods.
The benchmark return being the stock exchange index is then deducted from the funds’ rate of return. The market-adjusted return allows the determination of the rate of income exceeding the benchmark. The presented measure of returns is expressed with the following formula (Lee et al. 2008):
where rb is the benchmark-adjusted return of fund i in period t and rm is the return on the local stock market index in period t. This measure of returns enabled the classification of funds into groups of outperforming funds and underperforming funds in particular periods. However, due to the shortage of relevant databases in Poland, i.e. ones that would contain, for example, information about management fees, the applied performance calculation completely omits the expense ratio in fund returns.
As was mentioned in the first part, the main aim of this chapter is to examine whether the performance persistence phenomenon occurs in the Polish mutual fund market. Like Brown and Goetzmann (1995) did in one of their early studies, the benchmark used here was the median of the rates of return for each period (relative benchmark) and the value of the stock market index (absolute benchmark). Hence, the null hypothesis states that the results achieved in consecutive periods are unrelated to each other. It will be verified using the stochastic procedure, which will be supported with a few mobility measures.
The main research approach applied was a Markovian framework (see Kemeny and Snell 1976). The Markov chain used in this study is a special stochastic process with a countable state space and transitions at integer times. It could be said that a process ![]() is a Markov chain with the state space S if it takes value in set S and for every n ∈ N , for every S1, …, Sn, Sn+1, and for every t ∈ {n, n + 1, n + 2,...} , we have that:
is a Markov chain with the state space S if it takes value in set S and for every n ∈ N , for every S1, …, Sn, Sn+1, and for every t ∈ {n, n + 1, n + 2,...} , we have that:
From equation [11.3], it comes from an immediate interpretation of the Markov chain. Knowing the present state, it could be seen that the past of the process does not give us any further information about its future.
A crucial aspect in dealing with a Markov chain is its transition matrices, i.e. matrices
If the state space is finite, i.e. if S = {1, 2, 3, …, m} for some m ∈ N , then we can indicate
Each element of transition matrix Pt corresponds to the estimated probability of transiting from state i to state j across states. Moreover, it will be said that a Markov chain with transition matrices Pt is homogeneous if Pt does not depend on t. More precisely, there exists a matrix P such that for every t we have that P = Pt (see Filip and Rogala 2021).
The probability of events was calculated with the application of the moving ratio, which allows the determination of the number of times an outcome can occur compared to all possible outcomes within a chosen time horizon. The above assumptions enabled the estimation of transition probabilities on the basis of a six-month horizon for a monthly perspective, a four-quarter horizon for a quarterly perspective and a three-year horizon for a yearly perspective.
Moreover, it was decided to use several mobility measures to support the findings obtained based on the Markovian approach. The first of them was the immobility ratio (IR), which means the percentage of funds with the ability to maintain their returns (see Bigard et al. 1998). The IR was calculated as the number of funds characterized by predominance of good performance as well as bad performance in relation to the whole number of entities in the sample. The next two were MU and MD, which mean the percentage of funds whose returns improve from below the median to above the median (under- to outperformance) in general and the percentage of funds whose returns deteriorate from above the median to below the median (out- to underperformance) in most cases, respectively (Drakos et al. 2015). It should be noted that under the assumption of equal transition probabilities, each of these indices should be 33.3%.
11.4. Empirical results
When deciding to employ the Markovian framework, it had to be assumed that the probabilities of funds transiting between individual segments of the performance ranking in successive periods were uniform for funds. According to the assumptions of the applied approach, this means that all states of the Markov chain are equally likely to be visited and the process replicates at each consecutive stage independently.
In the successive transition matrices presented, the values in rows correspond to the probability of transiting from state i to state j across states (n = 2). The initial state in the first row means being a well-performing fund, whereas the initial state in the second row means being a poorly performing fund. In this section, instead of adopting the matrix approach, it was chosen to use tables with mobility measures added. The first of them is IR, which means immobility ratio. It will be a way to show a tendency for persistence, both winning persistence and losing persistence. The next two (MU and MD) indicate tendencies for performance reversal: improvement and deterioration, respectively.
11.5. Monthly perspective
It should be restated that the estimations of transition probabilities for a monthly perspective were made on the basis of observations from a six-month horizon. Table 11.1 presents the initial results for performance persistence in a short term.
Panel A: Probability of transiting between winning funds and losing funds
Table 11.1. Estimations for a monthly perspective. Source: own study
| Probability | Winners t+1 | Losers t+1 |
| Winners t | 0.5308 | 0.4692 |
| Losers t | 0.4637 | 0.5363 |
| IR = 0.0990 | MU = 0.4455 | MD = 0.4554 |
Panel B: Probability of transiting between outperforming funds and underperforming funds
| Probability | Winners t+1 | Losers t+1 |
| Winners t | 0.4598 | 0.5402 |
| Losers t | 0.4356 | 0.5644 |
| IR = 0.0594 | MU = 0.2475 | MD = 0.6931 |
With reference to the six-month horizon, the generated raw returns, which do not take market factors into account, seem to imply the existence of a short-term persistence. As follows from the data provided in Panel A of Table 11.1, the probability of remaining in the group of winning funds or losing funds is insignificantly higher (above 0.53) than that of transiting to any other state – for funds with reversal performance (approx. 0.47). This is not entirely confirmed by the results achieved as an effect of applying mobility measures. The degree of mobility measured by means of MU and MD indicates an increased propensity for transiting between individual performance ranking segments. Funds characterized by immobility were dominated by both funds with improving and ones with deteriorating positions.
The findings obtained after grouping funds by the market efficiency criterion are as expected. According to the results from Panel B of Table 11.1, the probability of failing to beat the market in consecutive periods was the highest of all permissible states, which is consistent with the efficient market theory. The noted lack of uniformity suggests that the percentage of funds whose positions deteriorated was larger than the percentage of funds whose positions improved. Moreover, it was noted that the funds that remained in their states as losers were observed most frequently, as far as a short term is concerned (probability at the level of 0.56). This proves the existence of performance persistence, but only with respect to the icy-hand effect. Mobility measures confirmed only the tendency for deteriorating performance (MD at the level of 0.69).
11.6. Quarterly perspective
In relation to a medium-term perspective, it also needs to be restated that the estimations of transition probabilities were made on the basis of observations from a four-quarter horizon. Table 11.2 presents results for performance persistence supported with mobility measures for a quarterly perspective.
Panel A: Probability of transiting between winning funds and losing funds
Table 11.2. Estimations for a quarterly perspective. Source: own study
| Probability | Winners t+1 | Losers t+1 |
| Winners t | 0.5702 | 0.4298 |
| Losers t | 0.4388 | 0.5612 |
| IR = 0.2857 | MU = 0.3673 | MD = 0.3469 |
Panel B: Probability of transiting between outperforming funds and underperforming funds
| Probability | Winners t+1 | Losers t+1 |
| Winners t | 0.4888 | 0.5112 |
| Losers t | 0.3618 | 0.6382 |
| IR = 0.2653 | MU = 0.1429 | MD = 0.5918 |
The results of the research, presented in Panel A of Table 11.2, suggest the persistence of quarterly raw returns of funds in consecutive periods in accordance with the selected classification criterion, namely the achievement or non-achievement of the median value in the performance distribution. The probability of transiting from the winner (loser) state to the loser (winner) state was lower (approx. 0.43) than that of remaining in the group of winners or losers (approx. 0.56–0.57). This is partly confirmed by the value of the immobility ratio (IR), which was determined to be relatively high, i.e. 0.29, yet not enough to exceed the expected level of 0.33.
The application of the stock market index as an absolute benchmark resulted, however, in a strong orientation of the recurrence towards the icy-hand phenomenon. Underperforming funds maintained the level of their performance in successive periods definitely more frequently (0.64) than funds characterized by different performance inertia (see Panel B of Table 11.2). Quite a high value of the probability of performance deterioration (0.51) also needs to be noted, since it was reflected in high values of the MD index (0.59), which show the percentage of the funds whose returns deteriorated in most cases from out- to underperformance.
11.7. Yearly perspective
Once again, it must be repeated that the estimations of transition probabilities for a yearly perspective were made on the basis of observations from a three-year horizon. Long-term observations were made for classifications on the basis of the relative (Panel A) as well as the absolute (Panel B) benchmark, and their results are presented in Table 11.3.
Panel A: Probability of transiting between winning funds and losing funds
Table 11.3. Estimations for a yearly perspective. Source: own study
| Probability | Winners t+1 | Losers t+1 |
| Winners t | 0.4725 | 0.5275 |
| Losers t | 0.5208 | 0.4792 |
| IR = 0.1353 | MU = 0.4265 | MD = 0.4382 |
Panel B: Probability of transiting between outperforming funds and underperforming funds
| Probability | Winners t+1 | Losers t+1 |
| Winners t | 0.3582 | 0.6418 |
| Losers t | 0.3562 | 0.6438 |
| IR = 0.2059 | MU = 0.1677 | MD = 0.6264 |
The last of the specified time horizons concerns a yearly perspective. As follows from the data provided in Panel A of Table 11.3, the performance persistence observed earlier decreases as the timeframe increases. For the sake of comparison, the probability of transiting from winning (losing) funds to losing (winning) funds was approximately 0.52–0.53. Mobility measures (MU and MD) also indicate high values, ones considerably exceeding the natural level of 0.33, let alone the low values of the immobility ratio (0.13). This means that transition probabilities are not uniform.
When the absolute benchmark (Panel B of Table 11.3), i.e. the stock market index in this case, was introduced as a classification criterion, the findings again turned out to be consistent with the efficient market hypothesis. The empirical transition probabilities were the highest when funds’ performance deteriorated in consecutive periods (0.64) or bad income persisted (0.64). The obtained results are supported by high values of the MD ratio (0.62), which signifies a high share of funds with deteriorating investment results
11.8. Conclusion
The aim of this chapter was to examine whether the performance persistence phenomenon occurred in a developing mutual fund market. The analysis was conducted for Polish equity funds from three time perspectives: monthly, quarterly and yearly. The empirical investigation was possible through the employment of Markov chains with transition matrices, supported with a few mobility measures.
The results suggest the existence of a limited performance persistence, especially when raw returns were applied. With reference to market-adjusted returns, used alternatively, only losing persistence was observed. It should be noted that the phenomenon decreases as the timeframe increases. However, the propensity for a relative repetition of mutual fund performance in consecutive periods, which takes the form of the icy-hand effect, as well as the higher transition probability for funds with deteriorating returns are consistent with the efficient market theory.
The applied research framework, which is still unknown in the area of finance, has proved useful in the verification of the performance persistence hypothesis. However, this study, along with the findings of Filip and Rogala (2021), may be considered as an introduction to the research on the performance of mutual funds in developing countries by means of stochastic processes and as a basis for further discussions and analyses in this respect.
11.9. References
Bigard, A., Guillotin, Y., Lucifora, C. (1998). Earnings mobility: An international comparison of Italy and France. Review of Income and Wealth, 44(4), 535–554.
Bota, G. and Ormos, M. (2017). Determinants of the performance of investment funds managed in Hungary. Ekonomska Istraživanja / Economic Research, 30(1), 1–14.
Brown, S.J. and Goetzmann, W.N. (1995). Performance persistence. The Journal of Finance, 50(2), 679–698.
Carhart, M. (1997). On persistence in mutual fund performance. The Journal of Finance, 52(1), 57–82.
Casarin, R., Pelizzon, L., Piva, A. (2008). Italian equity funds: Efficiency and performance persistence. ICFAI Journal of Financial Economics, 6(1), 7–28.
Czekaj, J. and Grotowski, M. (2014). Short-term persistence of the results achieved by common stock investment funds acting in the Polish Capital Market (in Polish). Ekonomista, 4, 545–557.
Dahlquist, M., Engstrom, S., Soderlind, P. (2000). Performance and characteristics of Swedish mutual funds. Journal of Financial and Quantitative Analysis, 35(3), 409–423.
Drakos, K., Giannakopoulos, N., Konstantinou, P.T. (2015). Investigating persistence in the US mutual fund market: A mobility approach. Review of Economic Analysis, 7, 54–83.
Filip, D. and Rogala, T. (2021). Analysis of Polish mutual funds performance: A Markovian approach. Statistics in Transition New Series, 22(1), 115–130.
Goetzmann, W.N. and Ibbotson, R.G. (1994). Do winners repeat? The Journal of Portfolio Management, 20(2), 9–18.
Grinblatt, M. and Titman, S. (1989). Mutual fund performance: An analysis of quarterly portfolio holdings. The Journal of Business, 62(3), 393–416.
Grinblatt, M. and Titman, S. (1992). The persistence of mutual fund performance. Journal of Finance, 47(5), 1977–1984.
Haslem, J. (2003). Mutual Funds: Risk and Performance Analysis for Decision Making. Blackwell Publishing, Malden.
Hendricks, D., Patel, J., Zeckhauser, R. (1993). Hot hands in mutual funds: Short-run persistence of relative performance, 1974–1988. Journal of Finance, 48(1), 93–130.
Huij, J. and Derwall, J. (2008). “Hot hands” in bond funds. Journal of Banking and Finance, 32(4), 559–572.
Huij, J. and Verbeek, M. (2007). Cross-sectional learning and short-run persistence in mutual fund performance. Journal of Banking and Finance, 31(3), 973–997.
Kemeny, J.G. and Snell, L.J. (1976). Finite Markov Chains. With a New Appendix “Generalization of a Fundamental Matrix”. Springer-Verlag, New York-Berlin- Heidelberg-Tokyo.
Koutsokostas, D., Papathanasiou, S., Eriotis, N. (2020). Short-term versus longer-term persistence in performance of equity mutual funds: Evidence from the Greek market. International Journal of Bonds and Derivatives, 4(2), 89–103.
Lee, J.S., Yen, P.H., Chen, Y.J. (2008). Longer tenure, greater seniority, or both. Evidence form open-end equity mutual fund managers in Taiwan. Asian Academy of Management Journal of Accounting and Finance, 4(2), 1–20.
Machnik, J. (2020). Performance persistence and gamma convergence in absolute return funds in Poland over the period 2011–2018. Financial Sciences, 25(2–3), 41–54.
Malkiel, B.G. (1995). Returns from investing in equity mutual funds 1971 to 1991. The Journal of Finance, 50(2), 549–572.
Otten, R. and Bams, D. (2002). European mutual fund performance. European Financial Management, 8(1), 75–101.
Wilkinson, N. and Klaes, M. (2012). An Introduction to Behavioral Economics, 2nd edition. Palgrave Macmillan, London.
Chapter written by Dariusz FILIP.