7
Advanced Topics
In this chapter, we discuss some advanced topics concerning MTT-semantics. These include work on propositional forms of judgmental interpretations (formal treatment of section 3.2.3), dependent event types (DETs; neo-Davidsonian event semantics with refined event types) and dependent categorial grammars (DCGs; Lambek-style categorical grammars with dependent types). The topics are discussed in the following three sections, which are independent of each other and, as such, can be read independently.
7.1. Propositional forms of judgmental interpretations: formal treatment
As explained in section 3.2.3, in MTT-semantics there are judgmental or ill-typed interpretations and, in order to interpret composite sentences, we may need to turn a judgmental interpretation into a proposition. These can be illustrated by examples whose interpretations involve the following, and the examples are taken from section 3.2.3 (pp. 62–64):
- – derivable judgments: examples include (3.62);
- – non-derivable judgments under negation: examples include (3.66) and (3.67);
- – ill-typed applications under negation: examples include (3.79) and (3.82).
There are propositional forms corresponding to the above judgmental interpretations. Here, we will study them in a more formal and precise way. This section should be read together with the informal introduction to propositional forms in section 3.2.3 and is based on various previous studies (Xue et al. 2018, 2020; Chatzikyriakidis and
Luo 2017b). The interested readers are encouraged to get more detailed information from these papers.1
We first introduce the true predicate pA used to give propositional forms for derivable membership judgments. Then, the NOT-operator and the operators IS and DO are studied: the last two can be defined in terms of NOT, used to give propositional forms for non-derivable judgments or ill-typed applications when they are used in negative contexts. The NOT-operator will be introduced axiomatically and it will be shown that the axiomatic laws for NOT can all be justified by means of the heterogeneous equality in type theory (McBride 2002; McBride and McKinna 2004). We shall also study conditions under which IS and DO can be used without resulting in overgeneration.
Propositional forms of derivable judgments. When a judgmental interpretation of the form a : A is derivable, its propositional form is given as pA(a) where, for any type A, pA is the “true predicate” defined as follows (the same as (3.64)):
As an example, the composite sentence (3.62), repeated here as (7.3), can be interpreted as (7.4), where pHuman(j) acts as the propositional form of j : Human.
(7.3) John is a human and he is happy.
(7.4) pHuman(j) ∧ happy(j)
Note that pA(a) is defined as true under the condition that a is of type A. So, pA(a) is not exactly the same as true, because the well-typedness of pA(a) presumes that a is of type A, while the well-typedness of true does not. Put in another way, the well-typed pA(a) carries more information than true, that is, it presumes that a is of type A. This is why pA(a) can play the role of being the propositional form of the derivable judgment a : A.
The NOT operator and definitions of IS and DO. Non-derivable judgmental interpretations and ill-typed applications may be meaningfully used in a negative context (see section 3.2.3 for examples (3.66), (3.67), (3.79), and (3.82)). Their propositional forms can be represented by means of the NOT-operator, whose type is given in (7.5): it takes four arguments to form a proposition NOT(A, p, B, b), where A and B are common nouns in CN, p : A → Prop is a predicate over A, and b is an object of type B. Intuitively, NOT(A, p, B, b) means that “b does not p” and, in particular, when p is pA (the true predicate over A as defined above), it means that “b is not an A”.
(7.5) NOT : ΠX:CN Πp:X → Prop ΠY :CN Πy:Y. prop
We can use NOT to define two operators IS and NOT by means of the following definitional abbreviations, where A, B : CN:2
(7.7) ISB(X, y) = ¬NOT(X, pX, B, y), for any X : CN and y : B
(7.8) DOA,B : (A → Prop) → B → Prop
(7.9) DOA,B(p, y) = ¬NOT(A, p, B, y), for any p : A → Prop and y : B
Sometimes (and usually in examples), we omit the subscripts to write IS(X, y) for ISB(X, y) and DO(p, y) for DOA,B(p, y). Intuitively, IS(X, y) and DO(p, y) mean that “y is an X” and “y does p”, respectively. Examples of how to use the operators IS and DO include those in section 3.2.3: (3.71) for (3.66), (3.72) for (3.67), (3.81) for (3.79) and (3.84) for (3.82).
Axiomatic laws for NOT and examples. The operator NOT is introduced axiomatically. In particular, it should satisfy the laws (A1−A5) below that govern its behavior, where A, B, C : CN and ![]() means that A ≤c B for some injective function c from A to B (i.e. for all x1,x2 : A, c(x1) = c(x2) implies that x1 = x2).
means that A ≤c B for some injective function c from A to B (i.e. for all x1,x2 : A, c(x1) = c(x2) implies that x1 = x2).

Using the operator DO, we can rewrite the above laws as ![]() below, which give intuitively more understandable readings. For example, the first law (A1) or
below, which give intuitively more understandable readings. For example, the first law (A1) or ![]() says that, when x : A (and hence p(x) is well-typed), DO(p, x) = ¬NOT(A, p, A, x) is logically equivalent to p(x) and, as a special case when p = pA, IS(A, x) = ¬NOT(A, pA, A, x) is logically equivalent to pA(x).
says that, when x : A (and hence p(x) is well-typed), DO(p, x) = ¬NOT(A, p, A, x) is logically equivalent to p(x) and, as a special case when p = pA, IS(A, x) = ¬NOT(A, pA, A, x) is logically equivalent to pA(x).
We now give an example for each law for illustration: Example (i) for ![]() and, for each example (i), (i′) explains how the law (Adi) works.
and, for each example (i), (i′) explains how the law (Adi) works.
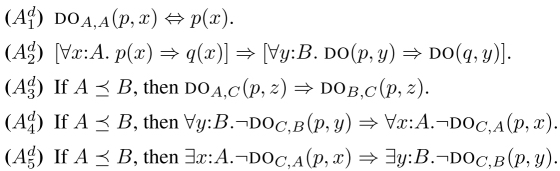
- (1) John is not a man.
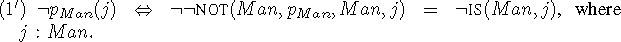
- (2) If a table doesn’t talk, then it doesn’t talk loudly.

- (3) If Teddy is a man, then Teddy is a human.
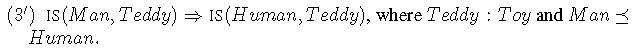
- (4) If tables do not talk, then red tables do not talk, either.

- (5) Since not every linguist is a logician, not every human is a logician.

Justification by heterogeneous equality. In the above, NOT has been introduced axiomatically to extend the underlying MTT. Is such an extension OK (for instance, is it logically consistent)? The answer to this question is positive; put in another way, this extension can be justified. There can be rather different ways to provide such a justification. For instance, one could go ahead to prove the meta-theoretic properties of the extended system, showing directly that the extension is consistent, among other things. However, this would have been an overkill, as anyone who has done such proofs knows that they are rather tedious and require a lot of effort. Another solution is to consider a known consistent extension E of the underlying type theory T and perform the following:
- 1) Known: T + E is consistent.
- 2) Define NOT (by means of E)in T + E.
- 3) Using the definition, prove that (Ai)(i = 1, ..., 5) are theorems in T + E.
- 4) Then, we know that T + NOT is consistent.
The question is: what is a suitable notion E for the above? Luckily, there is such a notion E: we can use JMeq, the heterogeneous equality that has been studied by McBride (McBride 2002; McBride and McKinna 2004).4 NOT can be defined by means of JMeq and its logical consistency can be shown as above: we shall only consider this briefly here – see Xue et al. (2020) for more technical details.
Usually, in a type theory, we can only form an equality proposition between two objects of the same type. A heterogeneous equality, however, allows us to talk about equality between arguments of different types. JMeq is such a heterogeneous equality, whose type is given in (7.10). Intuitively, JMeq(A, a, B, b) means that a and b are equal, although their types A and B may be different.
(7.10) JMeq : ΠA:Type Πx:A ΠB:Type Πy:B. prop.
NOT can be defined by means of JMeq as (7.11), according to which “b does not p”is defined as, for any x in A,if x equals b, then p(x) is not true.
(7.11) NOT(A, p, B, b) = ∀x:A. JMeq(A, x, B, b) ⇒ ¬p(x).
We can prove the following theorem to show that the axiomatic laws for NOT are all theorems in an MTT with JMeq and, as a corollary, since the extension with JMeq is logically consistent, so is the extension by NOT.
THEOREM 7.1.– If NOT is defined as in (7.11), (Ai)(i = 1, ..., 5) are all provable in the type theory extended by JMeq. □
Avoiding overgenerations. As mentioned above and informally introduced in section 3.2.3, some sentences whose interpretations involve non-derivable judgments or ill-typed applications may be meaningfully used in some negative contexts and, in such circumstances, they may be given legitimate semantics by the IS/DO-operators defined by means of NOT. However, it is obvious that we cannot use the operators like IS/DO without any restriction for, otherwise, overgeneration may occur. For instance, usually Table and Human do not share objects and, therefore, (7.14) is non-derivable and talk(t) in (7.15) is ill-typed (talk : Human → Prop). We do not use (7.16) and (7.17) to interpret (7.12) and (7.13).
(7.12) (#) John is a table.
(7.13) (#) Tables talk.
(7.14) j : Table
(7.15) ∀t : Table. talk(t)
(7.16) IS(Table, j)
(7.17) ∀t : Table. DO(talk, t)
In this section, conditions are studied so that the IS/DO-operators can be employed without risking overgeneration. We shall study two notions: the first being type disjointness and the second negative occurrence, both important for adequate use of IS and DO so that overgeneration would not occur (Luo and Xue 2020).
Type disjointness. When j : Man, the judgments such as j : Table and j : Woman are non-derivable. This non-derivability is not trivial: it assumes that the types Man be disjoint with Table and Woman. Here is a definition of the notion of type disjointness.
DEFINITION 7.1 (Type disjointness).– Let A and B be types. A and B are disjoint if there is no non-empty type C such that C ≤ A and C ≤ B. □
When non-derivable, a judgmental interpretation signals that the NL sentence is meaningless (at least usually so, unless in some fictional or special settings). Similarly, some propositional applications are ill-typed. For instance, with talk : Human → Prop and t : Table, talk(t) is ill-typed. Such ill-typed propositions usually represent meaningless sentences as well. If a judgment is non-derivable, then a use of NOT (and IS and DO) to represent the corresponding semantics could overgenerate: for example, overgeneration would happen if (7.19) and (7.21) were used to interpret (7.18) and (7.20), respectively, where we assume that Man/Woman and Human/Table be disjoint pairs.
(7.18) (#) John is a woman.
(7.19) (#) IS(Woman, j), where j : Man.
(7.20) (#) Tables talk.
(7.21) (#) ∀t : Table.DO(talk, t), where talk : Human → Prop.
Negative occurrences. In a semantic interpretation, the operators IS/DO can be employed to occur negatively (or to occur in a negative context). The notion of negative occurrence is defined using an auxiliary notion of ill-formed expression (IFE), inductively defined as follows:
- 1) a non-derivable judgment is an IFE;
- 2) an ill-typed propositional application is an IFE;
- 3) A ∧ B and A ∨ B are IFEs if either A or B is an IFE;
- 4) If ∀x:T.A and ∃x:T.A are IFEs if A is an IFE.
DEFINITION 7.2 (Negative occurrence).– Let A, B and C be of the form P1 ⊕...⊕Pn, where Pi’s are atomic, ⊕ ∈ {∧, ∨} and n ≥ 1. Then,
- – A and its subformulas occur negatively in ¬A;
- – A and its subformulas occur negatively in A ⇒ B;
- – B and its subformulas occur negatively in A ⇒ B if A is an IFE;
- – A subformula of A occurs negatively in ∀x:T.A and ∃x:T.A if it occurs negatively in A;
- – A formula occurs negatively in A ⇒ B ⇒ C if it occurs negatively in A ∧ B ⇒ C.
Here are some examples to illustrate how IS/DO-formulas may occur negatively in legitimate interpretations without overgeneration.
7.2. Dependent event types
Event semantics, whose study was initiated by Davidson (1967) and further studied in its neo-Davidsonian turn (see Parsons (1990) among others), has several notable advantages including Davidson’s original motive to provide satisfactory semantics for adverbial modifications. Dependent types provide useful tools in event semantics and, in this section, we sketch the work on DETs (Luo and Soloviev 2017, 2020) that are useful in providing adequate semantic interpretations. Although DETs can be added either to Church’s simple type theory or to MTTs, and hence used for either Montague semantics or MTT-semantics, in this section we only describe DETs in the Montagovian setting (and for how DETs work for event semantics based on MTTs, see Luo and Soloviev (2017, 2020)).
Davidsonian event semantics. The original motivation to introduce events in formal semantics was to solve a problem in interpreting adverbial modifications. Consider (7.28) and (7.29): intuitively we should have that the semantic interpretation of (7.29) implies that of (7.28). However, this is not a straightforward matter at all in a traditional Montagovian semantics without events. For instance, with butter : e → e → t and with_knife, in_kitchen : (e → t) → e → t, we may have (7.30) and (7.31) to interpret (7.28) and (7.29), respectively. But then, in order to have (7.31) ⇒ (7.30), we would have to resort to meaning postulates such as the we stating that if f is with_knife or in_kitchen, we always have f(p, x) ⇒ p(x). Such meaning postulates are rather ad hoc and unsatisfactory to say the least.
(7.28) John buttered the toast.
(7.29) John buttered the toast with the knife in the kitchen.
(7.30) butter(j, toast)
(7.31) in_kitchen(with_knife(butter(j)))(toast)
Davidson (1967) has introduced events in semantics, claiming that verbs tacitly introduce existentially quantified events and that verbs and adverbial phrases are predicates over events. In the neo-Davidsonian notations with thematic roles such as agent and patient, represented as functions agent and patient of type Event → e, the sentences (7.28) and (7.29) can be interpreted as (7.32) and (7.33), respectively, where Event is the type of all events and j and t are the interpretations of “John” and “the toast”, respectively.5
(7.32) ![]()
(7.33) ![]()
Such semantic interpretations with events are more satisfactory as far as adverbial modification is concerned: for instance, it is now obviously the case that (7.33) ⇒ (7.32) (with the former having more conjuncts), without the need to impose any meaning postulates.6
However, introducing events and the event quantifier may cause problems, paying a price if not done carefully. One of the problems is that the event quantifier may have unintended interferences with other quantifiers in semantic descriptions and some researchers have described this as an incompatibility problem between event semantics and Montague’s semantics or the event quantification problem (EQP) (Winter and Zwarts 2011; Champollion 2015; De Groote and Winter 2014). For example, for (7.34), the intended (neo-Davidsonian) event semantics can be (7.35), where talk : Event → t. However, there is another possible interpretation, that is, we move the event quantifier to the left to have a wider scope, resulting in (7.36). Although intuitively (7.36) is incorrect to interpret (7.34), it is acceptable just as the correct one: (7.36) is a legal formula; formally, it is difficult to say why (7.35) is a correct interpretation of (7.34) while (7.36) is not.
(7.34) Nobody talked.
(7.35) ¬∃x : e. [human(x) ∧∃v:Event. talk(v) ∧ agent(v) = x]
(7.36) (#) ∃v : Event. ¬∃x : e. human(x) ∧ talk(v) ∧ agent(v) = x
In order to avoid such incorrect interpretations as (7.36), researchers have made several proposals that we believe are either ad hoc or involving unnecessary complications.7 One of the applications of DET is that they provide a natural solution to the event quantification problem.
Dependent event types. In the Davidsonian event semantics in the traditional Montagovian setting (Davidson 1967; Parsons 1990), there is only one type Event of all events: for instance, the sentence (7.37) can be interpreted as (7.38), where talk, loud : Event → t.
(7.37) John talked loudly.
(7.38) ∃v : Event. talk(v) ∧ loud(v) ∧ agent(v) = j
We propose to consider refined types of events: rather than just a single type Event of all events, we introduce DETs, types of events that are dependent on some parameters such as agents and patients. For example, with Agent being the type of agents and for a : Agent, the dependent type EvtA(a) is the type of events whose agents are a. With DETs, (7.37) can be interpreted as (7.39), where talk(v) and loud(v) are well-typed because v’s type EvtA(j) is a subtype of Event.
(7.39)![]()
Note that we can now recover the thematic functions from events of a DET. For example, for a : Agent, we can define AGENTA[a] such that, for any event v : EvtA(a), AGENTA[a](v) = a.
In general, the parameters of DETs are usually names of thematic roles such as agents and patients. Formally, an n-ary DET is parameterized by objects of types A1, ..., An. Here, we shall only consider n-ary event types with n = 0, 1, 2:
- – when n = 0, the event type, usually written as Event, has no parameters. Event corresponds to the type of all events in the traditional setting;
- – when n = 1, we only consider EvtA(a) and EvtP (p), where a : Agent and p : patient, i.e. these are event types dependent on agents a or patients p. For example, if John is an agent with interpretation j, EvtA(j) is the type of events whose agents are John (see (7.39));
- – when n = 2, we only consider EvtAP (a, p) for a : Agent and p : patient, i.e. the event type dependent on agent a and patient p. For example, EvtAP (j, m) is the type of events whose agents and patients are John and Mary, respectively.
One may consider other schematic roles as parameters such as manners and utterers, which would lead to corresponding event types like EvtAM (a, m) of events dependent on agents and manners and EvtUM (u, m) on utterers and manners, as mentioned in Chapter 4.
Event types have natural subtyping relationships between them. For example, an event whose agent is a and whose patient is p is an event with agent a. In other words, the type EvtAP (a, p) is a subtype of EvtA(a). If we only consider the event types Event, EvtA(a), EvtP (p) and EvtAP (a, p), they have the following subtyping relationships:
(7.40) ![]()
which can be depicted as Figure 7.1.

Figure 7.1. Subtyping between DETs parameterized by agents and patients
DETs have several interesting applications, one of which is that they offer a natural solution to the event quantification problem.8 In the Montagovian setting with DETs (formally, Ce below), the EQP problem is solved naturally and formally – the incorrect semantic interpretations, obtained from the correct interpretations by swapping the event quantifier with others, are excluded because they are ill-typed and hence illegal formulae. For example, the sentence “Nobody talked” in (7.34) can be given semantics (7.41) and the corresponding incorrect semantics (7.42) is ill-typed (x in EvtA(x) is outside the scope of bound variable x (although intuitively it refers to it) and it is actually an undeclared free variable), and hence an illegal formula.
(7.41) ![]()
(7.42)![]()
Note that this is in contrast with those in the traditional setting without DETs where, for example, the incorrect semantics (7.36) is still well-typed and cannot be excluded formally without resorting to some informal principles. Put in another way, we claim that DETs offer a natural solution to the EQP problem and, compared with existing solutions with informal ad hoc principles such as those mentioned above, the solution comes naturally as a “side effect” of introducing DETs: it is formally disciplined and natural.
Ce: DETs in the Montagovian setting. Dependent event types can be introduced either in the Montagovian setting or in the MTT-setting and both have been studied in Luo and Soloviev (2017). Here, we shall only consider how to add DETs in the former, simple type theory with DETs, and show that the extension Ce is conservative over Church’s simple type theory C. The inference rules for Ce are given as follows: they are based on those for C, plus those for DETs.
– Rules for simple type theory: Ce contains all of the inference rules of C (see section 1.3.1 and Appendix A1.1) except that the λ-rule has one more premise (actually, a side condition) and becomes the following:
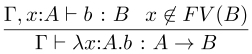
where FV (B) is the set of free variables occurring in B. Note that, in C, the side condition is not needed because in C there are no dependent types (and x does not occur free in B for sure).
- – Rules for thematic roles and DET.

- – Subsumption Rule.
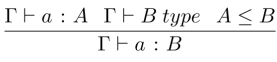
where the subtyping relation ≤ is the smallest partial order with respect to conversion ![]() (see footnote 10 on p. 8) such that the following two are the case:
(see footnote 10 on p. 8) such that the following two are the case:
1) it is contravariant with respect to arrow types: A → B ≤ A' → B' if A' ≤ A and B ≤ B';
2) the subtyping relations (7.40) between DETs, as depicted in Figure 7.1, hold.9
It is proven that the extension Ce of Church’s simple type theory by DET is conservative (Luo and Soloviev 2020) – the conservativity theorem below. Since a conservative extension essentially keeps the nice properties of the original system, including logical consistency, the corollary below follows.
THEOREM 7.2 (Conservativity).– Ce is a conservative extension of C.
PROOF.– Define R from Ce to C as follows: R maps Agent, patient, Event and ![]() to e, and every term that does not contain these types to itself (and this mapping is defined recursively). Then, it can be verified that R preserves derivability; i.e. for any derivation D, the image of D under R is a C-derivation. Note that R is the identity over any C-judgment and, therefore, if a C-judgment is derivable in Ce, then it is in C. Therefore, we conclude that Ce is a conservative extension of C. □
to e, and every term that does not contain these types to itself (and this mapping is defined recursively). Then, it can be verified that R preserves derivability; i.e. for any derivation D, the image of D under R is a C-derivation. Note that R is the identity over any C-judgment and, therefore, if a C-judgment is derivable in Ce, then it is in C. Therefore, we conclude that Ce is a conservative extension of C. □
COROLLARY 7.1 (Consistency).– Ce is logically consistent.
7.3. Dependent categorial grammars
In this section, we investigate how to extend categorial grammars with dependent types. First of all, note that categorial grammars are based on substructural calculi such as the Lambek calculus (Lambek 1958) and, therefore, to study the potential to extend it with dependent types requires one to understand whether it is possible, and if so, how to obtain dependent Lambek types. In this direction, the second author has studied dependent substructural types (Luo 2018c) and, in particular, dependent Lambek types in the context of investigating DCGs (Luo 2015), where it is shown how to consider them as syntactic categories corresponding to MTT-semantic types, a promising step toward establishing the theoretical basis for further investigations on DCGs. We shall study how such Lambek Π-types and Σ-types can be introduced and some of the consequences that this move will have on a categorial grammar implementing this kind of semantics. It is worth noting that some of the ideas reported here are still tentative and need be verified or further developed in the future.
We first discuss the CNs-as-types paradigm without dependent types within a categorial grammar setting and show that this opens up new possibilities with respect to selectional and syntactic restrictions. In particular, we show that we can choose between both stricter syntactic and semantic types, or stricter semantic types only. This has different consequences: in the first instance, sentences involving category mistakes are interpreted as semantically and syntactically infelicitous, while only as semantically infelicitous in the second case. We then move on and present a Lambek calculus with dependent types, as presented in (Luo 2015), which besides the type constructors in the Lambek calculus (Lambek 1958), further includes directed types for dependent products (Πr and Πl) and dependent sums (Σ∼ and Σ◦). We then discuss examples of how Lambek Π-types can be used for modeling sentences involving quantifiers and adverbs, as well as the relevance of directed Σ-types to adjectival modification. With respect to the latter, we argue that directed Σ-types can be used to model the stage versus individual level distinction associated with prenominal and postnominal position with a number of adjectives.
Categorial grammars: some historical notes. Categorial grammar is a family of related highly lexicalized formalisms aimed at dealing with NL syntax and semantics. The appeal that categorial grammars have to linguists is mainly due to the fact that they take language variation to be the result of lexicalization, where languagedependent properties are lexically driven, but, at the same time, language-independent properties are the result of applying a very small number of combinatory rules that order the individual lexical items according to the information in those items. The usual reference for categorial grammars is Lambek (1958), but the roots of categorial grammar go back to Ajdukiewicz (1935); Bar-Hillel (1953) or even Russell’s theory of types and Frege’s functional analysis of language (Morrill 2011). Ajdukiewicz’s version of categorial grammar is undirectional in the sense that the syntactic types do not include directional information. There are two basic types, sentence and name, and a basic operation, a cancelation schema, of the following sort:
Table 7.1. Directional syntactic types

![]() is an expression that reduces to B in case it is combined with an expression of type A. Lambek (1958) and Yehoshua et al. (1960) present directional versions of categorial grammar, where the cancelation schema is now split into two rules:
is an expression that reduces to B in case it is combined with an expression of type A. Lambek (1958) and Yehoshua et al. (1960) present directional versions of categorial grammar, where the cancelation schema is now split into two rules:
Let us see a simple example of how this works by first defining a toy lexicon. This will include a number of lexical items and their corresponding types in Table 7.1. With this in place, a simple derivation of the sentence “John loves Mary” proceeds as follows:
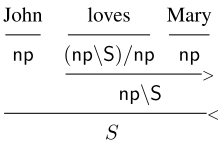
Lambda type semantics were later added on and a systematic mapping between categorial syntax and categorial semantics (lambda calculus) was offered (Van Benthem 1988; Moortgat 1988). Categorial grammars have gone a long way since then, and a number of different systems more flexible to handle the wealth of syntactic patterns found in natural language syntax have been proposed. Some of these extensions include Steedman’s Combinatory Categorial Grammar (CCG) (Steedman 2000), Levine and Kubota’s Hybrid Type Logical Grammar (HTLG) (Kubota and Levine 2015) and De Groote’s Abstract Categorial Grammars (ACG) (De Groote 2001), among others. There is a huge literature on dealing with various syntactic phenomena using these models or using some of the categorial grammar extensions for wide-coverage parsing in NLP as in the case of CCG. We will not be dealing with these more flexible versions of categorial grammar here, but we will instead try to initiate a discussion on how categorial grammar can be equipped with dependent types.
Motivation for dependent Lambek types. What is the motivation for introducing dependent types into a Lambek-style grammar? The way we see it there are at least two good reasons for such a move depending on the perspective one takes: for people working on some version of semantics that uses dependent typing, it offers them a syntactic calculus and a tight syntax/semantics correspondence. For those already working on categorial grammars of some sort, it offers them a more fine-grained semantic machinery. Introducing dependent types into categorial grammars is an endeavor that has not been attempted before, even though sparse discussions and proposals have been put forth. For example, Ranta (1998) discussed the idea of introducing type dependency into directed types and gave an inspiring example to represent directed types of quantifiers, although the paper did not study a formal treatment of such an extension. De Groote and Maarek (2007) studied how to extend the underlying type system for ACGs by (intuitionistic) dependent product types so that type families can be used to represent syntactic categories indexed by linguistic features. As mentioned earlier, the second author has developed dependent Lambek types for employing dependent types in the study of categorial grammars (Luo 2015, 2018c), which forms the basis for our study here.
On a more general level, combining resource sensitive types, for example, linear types like the ones used in linear logic (Girard 1987) with dependent types, has been a very interesting but, at the same time, very difficult research task. The main motivation in this line of work concerns applications of these calculi to programming and verification problems (see early work such as Cervesato and Pfenning (2002) and recent developments such as Krishnaswami et al. (2015); Vákár (2015)). However, how such a combination should be done is still widely open, on the one hand, and very much depends on the motivations in their applications, on the other hand.10
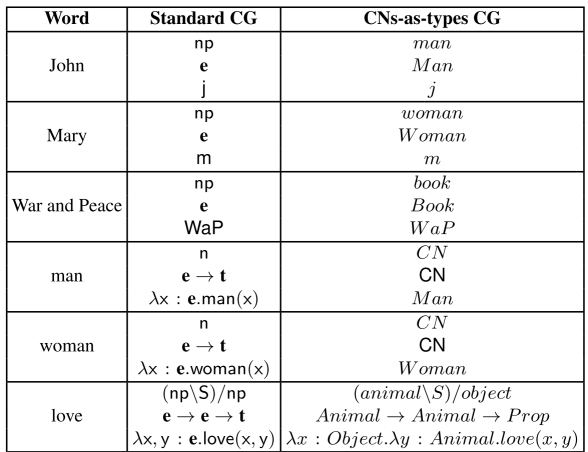
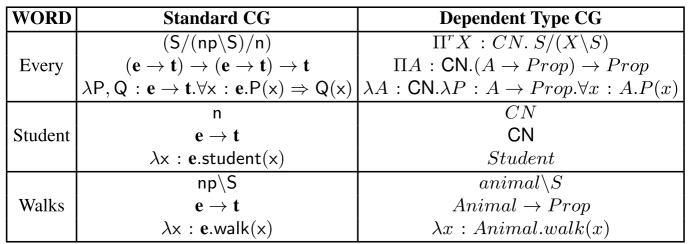
CNs-as-types categorial grammars. One of the interesting things to discuss before we move on and introduce dependent Lambek types is the correspondence between syntax and semantics when CNs are viewed as types (simple types only) rather than as predicates. Table 7.2 shows a comparison between a CG where CNs are types and a more standard CG. In effect, the difference in the two typing systems is as follows: in standard CG, the semantics language is MG, while in the case of the CNs-as-types CG, the typing system is the system used in MG with the addition of many constant types (type many-sortedness) and subtyping. We can immediately see that this minimally extended type system already has some interesting consequences. Note that the syntactic and semantic types, at least for proper names and common nouns, differ in the two versions of CG. In the case of the proper name “John” for example, the syntactic type is man, and the semantic type is Man for the CNs-as-Types CG, whereas in standard versions of CG, we have np and e for the syntactic and semantic type, respectively. For common nouns, what we get is CN in the syntax, CN as the semantic type and Man as the semantic interpretation in the CNs-as-types CG, whereas in standard CG, N is the syntactic type, e → t the semantic type and λx : e.man(x) the semantic interpretation. One of the things that should be already clear is that the two systems will give different results with regard to issues that have to do with selectional restrictions. For a standard CG, examples such as “War and Peace loves John” would be perfectly fine derivations (7.46), whereas for the CNs-as-types approach, the derivation would not work, given type mismatch (7.47):
Table 7.2. Comparison of simple lexical entries in standard versions of categorial grammar and the CNs-as-types categorial grammar. Each word is associated with a syntactic type, a semantic type and its semantics
(7.46) 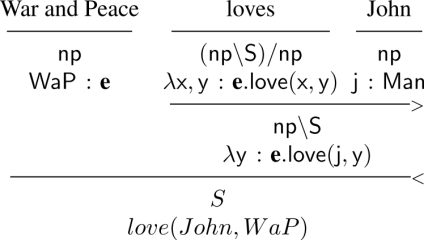
(7.47) 
It seems to us that there is an intermediate possibility between the possibilities already presented, i.e. the possibility that allows sentences such as “War and Peace loves John” to be parsed and receive semantics (standard CG, (7.46)), and the possibility that disallows this option (7.46). The intermediate view says that sentences like these are well-formed syntactically but semantically infelicitous. This is pretty much the middle ground between the two approaches we have presented here and could be obtained assuming that the syntactic types are more flexible than semantic types in the following sense: we could imagine that the syntactic type for “John” is not man but rather a more general syntactic type object, while its semantic type is Man. Similarly, for love, we assume the syntactic type (objectS)/object, but its semantic type is Object → Animal → Prop.11 These assumptions would give us a well-formed parse but infelicitous semantics:
This point is an interesting and important one and which version of the CNs-as-types CG to use (many types for both syntactic and semantic types or only for the latter types) needs more discussion. We leave this issue as a subject for future research.
We are now ready to introduce dependent Lambek types and discuss their use.
Preliminaries to the introduction of dependent Lambek types. Introducing dependent types into a Lambek calculus, we consider a calculus with contexts having two parts:
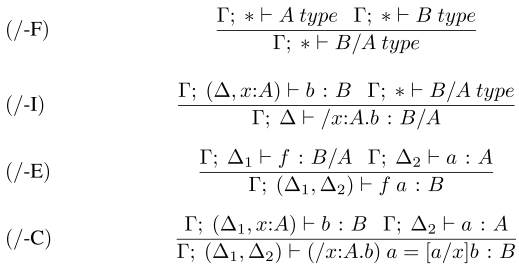
Figure 7.2. Rules for directed Lambek types B/A.
where Γ is an intuitionistic context (whose variables can be used for any times in a term) and Δ is a Lambek context (or ordered context). Types may only depend on ordinary variables in Γ, but not on Lambek variables in Δ.
Since we are going to introduce dependent types in which objects may occur, we need the following equality typing rule which says that computationally equal types have the same objects:

Contexts of the above form obey the following validity rules where, in the last two rules, x ![]() FV (Γ, Δ):
FV (Γ, Δ):
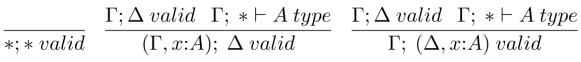
For variables, we have
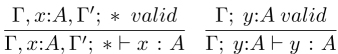
We can now present the directed types in the Lambek calculus. The rules for the directed types B/A are given in Figure 7.2.
Introducing dependent Lambek types
Directed dependent products. Dependent product types (Π-types) are split into directed dependent products (Πr and Πl). The rules for Πr-types are given in Figure 7.3. The rules for Πl-types, omitted here, are symmetric with term constructors λlx:A.b and appl(a, f).

Figure 7.3. Directed Πr-types
Table 7.3. Sample lexicon for a dependent CG in comparison with a standard CG
Having introduced directed Π-types, we can have a look at more elaborate examples and see how they are compared with standard CG. Consider the simple example in (7.49):
(7.49) Every student works.
Let us first see the lexicon used, again compared with standard CG. This is shown in Table 7.3. In this table, student is a subtype of animal (and, hence by contravariance, animalS is a subtype of studentS). Type S corresponds to the the universe of propositions Prop in the semantics. The derivation of (7.49) is shown in (7.50):
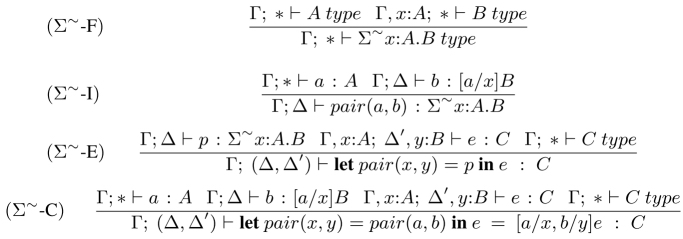
Figure 7.4. Rules for Σ∼-types
(7.50) 
Similar examples can be devised for sentences involving VP adverbs, where their syntactic type will be ΠrX : CN. (XS)(XS) (with X implicit) and their usual semantic type as discussed in Chapter 4, i.e. ΠA : CN.(A → Prop) → (A → Prop). Other interesting uses of the Π include its employment in the semantics for subsective adjectives. This is a case that we want to discuss in relation with our discussion on dependent Lambek types. But, to do that, we have to introduce Lambek Σ-types. To this we turn now.
Directed dependent sums. Dependent sum types (Σ-types) are split into reverse dependent sums (Σ∼) and concatenation dependent sums (Σ◦). The rules for Σ∼-types are given in Figure 7.4, while the rules for Σ◦-types are symmetric and omitted. We remark that the universe CN is closed under Σ∼ and Σ◦. A classic use of dependent Σtypes concerns, as we have extensively discussed in this book, adjectival modification, and in general common noun modification. The directed dependent sum types may thus be used to analyze modification that can come in both directions. For example, we can think of the following two cases:
(7.52) Student who is diligent
Directed dependent sum types may be used to analyze these cases. Assuming that B : AS, let us use Σ∼(A, B) to abbreviate Σ∼x:A.(x B) and Σ◦(A, B) to abbreviate Σ◦x:A.(x B). Now, with diligent : humanS, we can use Σ∼(Student, diligent) to describe the modified common noun diligent student, and Σ◦(Student, diligent) to analyze student who is diligent. Of course, we are here skipping the details of parsing the relative clause,12 but the general idea is that “who is diligent” should get the same semantics as “diligent”. If this happens, then the directed Σ can come at play in the way described. The semantics in both cases, the right and left versions of Σ are the same in these examples. However, we have cases of adjectives that can appear both prenominally and postnominally with an effect on their semantic interpretation: this is the very well-known case of adjectives like “visible”, “responsible” among others, that have a stage-level interpretation when interpreted post-nominally, while underspecified between an individual-level and stage-level interpretation in pre-nominal position.13 There are different ways we can approach the difference between the two types of adjectival modification, and it is not our intention to get into a deep discussion of their analysis in MTT-semantics. Our goal is to rather exemplify the usefulness of directed sums. The difference in semantic interpretation is one where the property expressed by the stage-level adjective is only valid temporarily (valid in a stage). This is not necessary the case in individual-level adjectives. Let us give a sketch of how this can be done with the help of directed sums: assume for t : Time, Staget : Prop → Prop, the type representing the collection of propositions that hold at time t. Assume now an adjective such as “visible” of type ΠA : CN. A → Prop. The directed sums can be used to get the different interpretations, individual and stage level (with A implicit):
(7.53) Σ∼(stars, visible) → Σ(Stars, visible)
(7.54) Σ◦(stars, visible) → Σ(Stars, Staget(visible))
REMARK.– On the relation between Σ-types in syntax and semantics. What we have seen so far are cases where some correspondence between directed sums in the syntax and Σ-types on the semantic level exists. However, there are cases that this might not be needed, or even should not be the case. In the CNs-as-types paradigm, besides the option of interpreting CNs as plain types, we can use Σ-types for their interpretation. For example, “man” can be interpreted both as Man or as the Σ-type Σx:Human.male(x) (among other options). In case we go for the Σ-type interpretation, it does not make any sense to involve directed sums in the syntax, but rather a syntactic constant man. The reason for this is that the purpose of the syntactic calculus is to put words together into sentences and decide which sentences are well-formed syntactically and which sentences are not. Assuming a directed sum in the case of “man” would create the need for empty categories, silent words that are not present in the actual NL string. For example, if we assume that the directed sum follows the semantic interpretation Σx:Human.male(x), one will have to assume that type Human and the predicate male can be found somewhere in the syntactic derivation. This seems counterintuitive to say the least. Of course, one can make this work and introducing categories not present in the actual NL string is not itself new in linguistics, but for this particular case, it is very unclear what is the gain of doing so, if any. □
With this last note, we will stop our brief discussion on extending CGs with dependent types. We have only touched on the surface of it, but we hope that we have managed to exemplify some of the advantages for such a move. In the future, we plan to further expand on these ideas, ideally also implementing a dependent CG that will be able to parse NL sentences and output MTT-semantics. Such work could easily connect and develop into more applied tasks such as natural language inference (NLI), in the same spirit with recent work by Mineshima et al. (2015), Bernardy and Chatzikyriakidis (2017) and Bernardy and Chatzikyriakidis (2019), among others.
- 1 In this section, we shall work in the impredicative type theory UTT (Luo 1994). For a predicative type theory, we may replace the totality Prop by some predicative universe (see, for example, the system MLTTh in Luo (2018a)) and then similar results can be obtained.
- 2 In Xue et al. (2018) (definition 3.1), we have defined the proposition PA,B : B → Prop.In the current notation, we have PA,B(t) = ISB(A, t).
- 3 That Σ(Table, red) Table, i.e. Σ(Table, red) is a subtype of Table via an injective coercion, is due to the assumption of proof irrelevance: for red : Table → Prop, red(x) = red(y) for any x, y : Table. See Luo (2012a, 2018a) for more on proof irrelevance.
- 4 JMeq is proposed and named “John Major equality” by McBride (2002).
- 5 Note that, traditionally, most people do not write the type Event explicitly and just use notational conventions. For example, we would usually write (7.32) as ∃v. butter(v) ∧ agent(v) = j ∧ patient(v) = t, omitting Event and saying that the variable v ranges over events. Also, when writing ∃v, some can even mean ∃v:e, for v to range over all entities (and events are just special entities). We take it to mean ∃v:Event and leave it open as to whether Event ≤ e (i.e. whether events are entities).
- 6 Event semantics also has other advantages. As an example, the semantics based on events implies that adverbial modifications commute to each other, as pointed out by Landman (2000); otherwise, we would have to add further meaning postulates to enforce such constraints.
- 7 These proposals include, for example, Landman’s (1996) informal Scope Domain Principle whose adherence would disallow incorrect interpretations and Champollion’s (2015) consideration of sets of events, which would bring complications whose implications on intuitive correctness and compositionality are unclear.
- 8 Among others, another use of DETs is to facilitate the treatment of selectional restriction in event semantics, especially in the MTT-setting (Luo 2018a).
- 9 Note that, in the Montagovian setting, the subtyping relations between DETs are subsumptive.
- 10 The interested reader may consult further papers in the literature to find out more about this. One of the key technical problems is whether to allow types to depend on substructural variables like Lambek/linear variables. Such a decision would make the complexity of the substructural calculi substantially different (see, for example, Luo (2018c) for a technical development in this respect when types can depend on linear variables).
- 11 Actually, we can envisage the use of np instead of object, as in more standard versions of CG. There are countless possibilities on how to structure the typing systems and in what level of granularity. The question of how different in terms of fine-grainedness the syntactic and semantic systems should be, is interesting and should be pursued further in future work.
- 12 Parsing relative clauses using CGs is not anything difficult. The interested reader can have a look at any introductory paper or book in CG for more information. Here, we are just skipping the details of how this derivation will look like in a Dependent CG setting.
- 13 See more on the individual and stage-level distinction in Carlson (1977); Chierchia (1995); Kratzer (1995), among others.

