Category theory really isn't too difficult a concept. Its place in math is large enough to fill up an entire graduate-level college course, but its place in computer programming can be summed up quite easily.

Einstein once said, "If you can't explain it to a 6-year-old, you don't know it yourself". Thus, in the spirit of explaining it to a 6-year-old, category theory is just connecting the dots. Although it may be grossly over-simplifying category theory, it does do a good job of explaining what we need to know in a straightforward manner.

First you'll need to know some terminology. Categories are just sets with the same type. In JavaScript, they're arrays or objects that contain variables that are explicitly declared as numbers, strings, Booleans, dates, nodes, and so on. Morphisms are pure functions that, when given a specific set of inputs, always return the same output. Homomorphic operations are restricted to a single category, while polymorphic operations can operate on multiple categories. For example, the homomorphic function multiplication only works on numbers, but the polymorphic function addition can work on strings too.

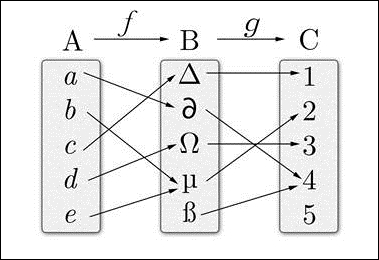
The following diagram shows three categories—A, B, and C—and two morphisms—ƒ and ɡ.

Category theory tells us that, when we have two morphisms where the category of the first one is the expected input of the other, then they can be composed to the following:

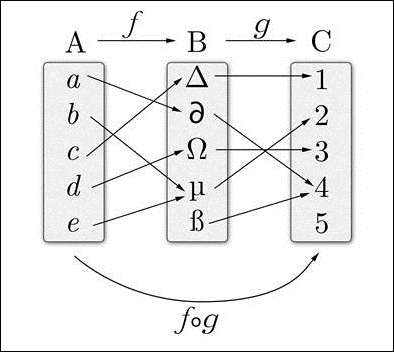
The ƒ o g symbol is the composition of morphisms ƒ and g. Now we can just connect the dots.

And that's all it really is, just connecting dots.

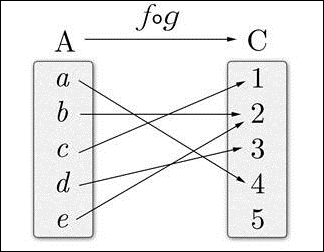
Let's connect some dots. Categories contain two things:

These are the terms given to category theory by mathematicians, so there is some unfortunate nomenclature overloading with our JavaScript terminology. Objects in category theory are more like variables with an explicit data type and not collections of properties and values like in the JavaScript definition of objects. Morphisms are just pure functions that use those types.

So applying the idea of category theory to JavaScript is pretty easy. Using category theory in JavaScript means working with one certain data type per category. Data types are numbers, strings, arrays, dates, objects, Booleans, and so on. But, with no strict type system in JavaScript, things can go awry. So we'll have to implement our own method of ensuring that the data is correct.

There are four primitive data types in JavaScript: numbers, strings, Booleans, and functions. We can create type safety functions that either return the variable or throw an error. This fulfils the object axiom of categories.

var str = function(s) {
  if (typeof s === "string") {
    return s;
  }
  else {
    throw new TypeError("Error: String expected, " + typeof s + " given.");   
  }
}
var num = function(n) {
  if (typeof n === "number") {
    return n;
  }
  else {
    throw new TypeError("Error: Number expected, " + typeof n + " given.");   
  }
}
var bool = function(b) {
  if (typeof b === "boolean") {
    return b;
  }
  else {
    throw new TypeError("Error: Boolean expected, " + typeof b + " given.");   
  }
}
var func = function(f) {
  if (typeof f === "function") {
    return f;
  }
  else {
    throw new TypeError("Error: Function expected, " + typeof f + " given.");   
  }
}

However, there's a lot of repeated code here and that isn't very functional. Instead, we can create a function that returns another function that is the type safety function.

var typeOf = function(type) {
  return function(x) {
    if (typeof x === type) {
      return x;
    }
    else {
      throw new TypeError("Error: "+type+" expected, "+typeof x+" given.");
    }
  }
}
var str = typeOf('string'),
  num = typeOf('number'),
  func = typeOf('function'),
  bool = typeOf('boolean'),

Now, we can use them to ensure that our functions behave as expected.

// unprotected method:
var x = '24';
x + 1; // will return '241', not 25

// protected method
// plusplus :: Int -> Int
function plusplus(n) {
  return num(n) + 1;
}
plusplus(x); // throws error, preferred over unexpected output

Let's look at a meatier example. If we want to check the length of a Unix timestamp that is returned by the JavaScript function Date.parse(), not as a string but as a number, then we'll have to use our str() function.

// timestampLength :: String -> Int
function timestampLength(t) { return num(str(t).length); }
timestampLength(Date.parse('12/31/1999')); // throws error
timestampLength(Date.parse('12/31/1999')
  .toString()); // returns 12

Functions like this that explicitly transform one type to another (or to the same type) are called morphisms. This fulfils the morphism axiom of category theory. These forced type declarations via the type safety functions and the morphisms that use them are everything we need to represent the notion of a category in JavaScript.

var obj = typeOf('object'),
obj(123); // throws error
obj({x:'a'}); // returns {x:'a'}

var obj = function(o) {
  if (Object.prototype.toString.call(o)==="[object Object]") {
    return o;
  }
  else {
    throw new TypeError("Error: Object expected, something else given."); 
  }
}

var objectTypeOf = function(name) {
  return function(o) {
    if (Object.prototype.toString.call(o) === "[object "+name+"]") {
      return o;
    }
    else {
      throw new TypeError("Error: '+name+' expected, something else given.");
    }
  }
}
var obj = objectTypeOf('Object'),
var arr = objectTypeOf('Array'),
var date = objectTypeOf('Date'),
var div = objectTypeOf('HTMLDivElement'),