Chapter 2
Introduction to Algebra
Abstract
This chapter provides an introduction to algebra through learning basic principles of addition, multiplication, exponents, and radicals. The chapter shows addition, subtraction, multiplication, and division of polynomials. Also, the chapter introduces ratios, proportions, and variation.
Keywords
Algebra; Exponent; Radical; Ratio; Polynomial; Proportion; VariationWhen solving problem, dig at the roots instead of just hacking at the leaves.
Anthony J. D'Angelo

James Prescott Joule (1784–1858), an English physicist who studied the nature of heat and established its relationship to mechanical work. He therefore laid the foundation for the theory of conservation of energy, which later influenced the First Law of Thermodynamics. He also formulated the Joule's laws which deal with the transfer of energy.
Introduction
In this chapter, we will discuss useful and important basic topics of introductory algebra that are essential for easier understanding of technical and applied mathematics.
2.1. Introduction to algebra
In algebra, some values are known but others are either unknown or not specified, which can be represented by letters or variables. Algebra performs mathematical operations on numbers and variables (unknown numbers), in order to find the values of variables.
Algebra uses signs to represent operations. The study of algebra involves the use of equations to solve various problems. Today, technicians and engineers are required to learn algebra to solve general and specific problems related to their fields and new technologies.
In algebra, an expression is a combination of letters that represent numbers known as variables, separated by operations creating terms. For example, 3x − 1 is an expression with two terms. The number or constant in front of the variable of an expression is called a coefficient. For the above example, 3 is the coefficient of x. An expression is a mathematical statement that does not contain an equal sign (=), but it can contain numbers, variables, and operators (+, –, ×, ÷). Equations are expressions followed by an equal sign.
In algebra, we use formulas that are shortened rules for employing letters as symbols to represent quantities. For example, we use the letter l to represent the length, the letter w to represent the width, and the letter A for area. We can write the formula for the area of a rectangle as A = l × w.
Example 1
Find the coefficients of the following expressions:
(a) 25x − y
(b) 7t + 3z
Solution
(a) 25 is the coefficient of x and −1 is the coefficient of y
(b) 7 is the coefficient of t and 3 is the coefficient of z
Some expressions contains more than one grouping of symbols in parentheses ( ) or brackets [ ]. In this case, you need to compute the innermost grouping first and work outward.
When terms involve the same letter with different coefficients in an expression, we call them like terms. For example, the expression 5x − 2y + 7x + 4y have two like terms 5x with 7x and −2y with 4y. Usually an expression can be simplified by adding and subtracting the like terms (apples to apples and oranges to oranges).
Example 2
Compute the following
(a) x(a + 3a) − 2
Solution
(a) First we solve the operation in parentheses, which is a + 3a = 4a, then we multiply the result 4a by x, which is 4ax, then we subtract 2 from 4ax to give us 4ax − 2.
(b) First we solve the operation in parentheses from a + 3a = 4a, then we multiply the result, 4a, by x, which is 4ax. Then we subtract 2 from 4ax to give us 4ax − 2. Next, we multiply by 5 to give us 20ax − 10.
Example 3
Simplify the expression 8x − 3y − 2x + 15y.
Solution
First, we collect the like terms for x, which are 8x − 2x = 6x, and the same for the y as −3y + 15y = 12y. Therefore, the expression 8x − 3y −2x + 15y can be simplified to 6x + 12y.
Substitution is used in algebra to find a numerical value of a variable in an expression. It can be done by assigning a particular number value to a variable.
Example 4
Let y = x − 2 and x = 5, find the value of y.
Solution
We need to substitute 5 for x to get the value of y as y = 5 – 2 = 3.
2.1.1. Basic principles of addition
We can summarize the basic principles of addition as in the table below considering a, b, and c are real numbers.
We will apply the above principles on algebra as in the below examples. We use x and y to represent variables.
Example 1
(a) 5x + 2y = 2y + 5x
(b) 7x + (3y + 9) = (7x + 3y) + 9
(c) 2y + 3y = y (2 + 3)
(d) 0 + 6x = 6x
(e) 7x + (−7x) = 0
2.1.2. Basic principles of multiplication
The basic principles of multiplication are summarized as in the below table with consideration that a, b, and c are real numbers.
Again, we applied these principles to algebra as in the below examples. It is important to know that ab = a × b = a·b.
Example 1
(a) (5x)(2y) = (2y)(5x) = 10xy
(b) 7x [(3y)(9)] = [(7x)(3y)]9 = 189xy
(c) 5[t + 3] = 5t + 15
(d) 1·6x = 6x
(e) 7x (1/7x) = 1
(f) x·6 = 6x
(g) (–9t)t = −9t2
We summarized some of the most basic algebraic operations and the way they simplified as in the below table with consideration that a, b, c, and d are real numbers.
When several operations exist in a single expression, then we need to follow the order of operations as we start first with parentheses, second with exponent, third with multiplication or division, left to right, and fourth with addition or subtraction, left to right.
Example 2
Simplify the following:
(a) 55 − (6 − 2) × 32
(c) x + (−y)
(d) 
(e) x × 0
(f) 0/x
(g) 
(h) x(−y)
(i) (−x)y
(j) (−x)(−y)
(k) −(−x)
(l) 
(m) 
(n) 3x = 3y
(o) 
(p) a(b = 0)
(q) 
(r) 
(s) 
(t) x − (3z + t)
(u) 7z − (y − x)
Solution
(a) 55 − (6 − 2) × 32 = 55 – 4 × 32, we start first with parentheses
=55 – 4 × 9, then exponent
=55 − 36, multiplication
=19, last subtraction
(b) 7[5 − (a + b)] = 7[5 – a − b] = 35 − 7a − 7b
(c) x + (−y) = x − y
(e) x × 0 = 0
(f) 
(g) 
(h) x(−y) = −(xy) = −xy
(i) (−x)y = −(xy) = −xy
(j) (−x)(−y) = xy
(k) −(−x) = x
(l) 
(m) 

(n) 
(o) 

(p) a(b = 0) = a × 0 = 0
(q) 
(r) 
(s) 
(t) x − (3z + t) = x − 3z − t
(u) 7z − (y − x) = 7z – y + x
Example 3
Simplify the following:
(a) 
(b) 
(c) 
(e) 3x (2 − 7x)
(f) 6x – 2 – 3x)
(g) 5y − (−5x + 2y)
(h) (−7)(3x)
(i) (−2x)(−3y)
(j) (3x − 2)(3x + 2)
(k) 
Solution
(a) 
(b) 
(c) 
(d) 
(e) 3x (2 − 7x) = 6x − 21x2
(f) 6x – (2 – 3x) = 9x – 2
(g) 5y − (−5x + 2y) = 3y + 5x
(h) (−7)(3x) = −21x
(i) (−2x)(−3y) = 6xy
(j) (3x − 2)(3x + 2) = 9x2 − 4
(k) 
We summarized some of the most common expansions and factors and the way they simplified as in the below table with consideration that a and b are variables.
Example 4
(a) (x − y)(x + y) = x2 − y2
(b) (x − z)(x2 + xz + z2) = x3 − z3
(c) (x + y)(x2 – xy + y2) = x3 + y3
(d) (x + y)2 = (x + y)(x + y)
2.1.3. Exponent and radicals
The expression an is a combination of the power n, which is the exponent, and a which is the base.
So, a power or exponent indicates how many times the base is multiplied by itself. The power is written in exponent form to represent the number of factors.
For example, 5 × 5 is called the second power and can be written in exponent form as 52.
We read 52 as 5 power of 2. The 5 is called the base and the 2 is called the exponent. When no exponent is written with a number, it is assumed to be one. For example, 5 = 51.
Example 1
Find the value of 34.
Solution
34 = 3 × 3 × 3 × 3 = 81.
Based on the definition of exponent, we can define the exponent an when n is zero or negative values.
We can summarize the rules of power as:
We summarize the operations with zero as in the below table with consideration that a is a real number.
For a and b are real numbers, and m and n are natural numbers.
We summarize the common properties of square root as in the below table.
Example 2
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
2.1. Exercises
In problems 1–6, perform the indicated operations using exponents, and write each answer in a simple form.
1. 3 × 3
3. 2 × 16
4. 3 × 9
5. mn × mn × mn × mn
6. vt × vt × vt
In problems 7–22, find the value for n for which each statement is true.
7. 24 × 25 = 2n
8. 24 × 26 × 28 = 4n
9. 3n × 35 = 311
10. 3n × 39 × 34 = 321
11. 7(72 × 73) = 7n
12. 58(54 × 5) = 5n
13. 2n × 2n = 1
14. 2n × 23n = 1
15. 3n–1 = 3
16. 32n+1 = 34
17. 25 × 35 = 6n
18. 27 × 37 = 6n−1
19. 210 × 57 = 23 × 10n+1
20. 312 × 58 = 34 × 15n−1
21. 45 × 35 = n5
22. 27 × 97 = n7
In problems 23–28, perform each of the indicated operations.
23. 27
24. 28
25. (23)2
26. (32)3
27. (2·32)2
28. (53 × 32)0
In problems 29–36, write each rational expression in lowest terms.
29. 
31. 
32. 
33. 
34. 
35. 
36. 
2.2. Addition, subtraction, multiplication, and division of monomials
A monomial is one variable that is the product of a constant (a letter that stands just for one number) and a variable with a nonnegative integer power. Recall, integer is a set of {…, −2, −1, 0, 1, 2,…}
c = a constant (coefficient of the monomial)
x = a variable
k = an integer (degree of monomial)
Exponent (power) is a small number above the variable or number (called base) to indicate the number of times a number is multiplied by itself.
For 
 k factors
k factors
x = base
k = exponent
Example 1
(a) x0 = 1
(b) x1 = x
(c) x2 = x·x
(d) 
(e) 
Example 2
7x3 is a monomial with a coefficient 7 and of a degree 3.
Note that  , if k ≠ 0
, if k ≠ 0
Two monomials can use addition and subtraction between them only when they are like terms (same variable with same degree).
Example 3
(a) 3x2 + 5x2 = (3 + 5)x2 = 8x2
(b) 3x2 + 5x ≠ 8x2
(c) −3V + 9V = (−3 + 9)V = 6V
(d) 5I3 − 13I3 = (5 − 13)I3 = −8I3
A term is an expression, for example, 6t5, is a term with number 6 as coefficient and t as variable, and 5 as the exponent. The expression t5 means t·t·t·t·t. There are two types of terms: first, like terms, which are terms having the same variable and same exponent; second, unlike terms, which are terms that do not have the same variable and the same exponent. For example, z and z2 are unlike terms, whereas, 8z5 and 3z5 are like terms.
2.2.1. Rules for multiplication of monomials
The rules for multiplication of monomials are summarized in the below table.
Example 1
(a) 3x2·2x5 = (3·2)x2+5 = 6x7
(b) (x2)5 = x2·5 = x10
(c) (2x2)3 = 23x2·3 = 8x6
2.2.2. Rules for division of monomials
The rules for multiplication of monomials are summarized in the below table.
Example 1
Simplify the following
(a) 
(b) 
(c) 
(d) 
(e) 19x−3
Solution
(a)  or by cancellation
or by cancellation 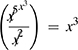
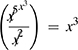
(b) 
(c) 
(d) 
(e) 
A binomial is the sum or difference of two monomials that are not like terms.
2.2.3. Addition, subtraction, multiplication, and division of polynomials
A polynomial is a monomial or a finite sum of monomials. In other words, a polynomial is a term or a finite sum of terms in which all variables have exponents of whole numbers and no variables with negative exponents.
For example, the following are polynomials:
−5, 3n, and 6y3 + 2y2 + x.
For example, 5z3 + 3z − 1 is polynomial with coefficients 5, 3, −1 with degree of 3. Note that  is not a polynomial.
is not a polynomial.
A polynomial can have more than one variable. A term (monomials that make up a polynomial) with more than one variable has a degree of the sum of all the exponents of the variables.
The degree of a polynomial in more than one variable is equal to the greatest degree of any term in the polynomial.
For example, 5z3x6 has a degree of 9, and z3x + 3xy − 1 has a degree of 4.
There are four types of polynomials:
1. Trinomial: a polynomial containing exactly three terms
2. Binomial: a polynomial containing exactly two terms
3. Monomial: a single term polynomial
4. Just polynomial
Example 1
1. z3x + 3xy − 1 is polynomial of type trinomial
2. z3x + 3x is polynomial of type binomial
3. 3xy is polynomial of type monomial
4. z3x + 3xy + 7t − 17n is polynomial
Example 2
Add or subtract the following polynomials:
(a) (2z3 + 4z3 − 3z) − (z3 + 6z2 − z) + 17
(b) −3(z2 − 4z −3) + (z2 + z)
Solution
(a) Distribution of the minus sign and then combining like terms.
(2z3 + 4z3 − 3z) − (z3 + 6z2 − z) + 17
=2z3 + 4z3 − 3z − z3 − 6z2 + z + 17
=(2z3 + 4z3 − z3) − 6z2 + (−3z + z) + 17
=5z3 − 6z2 − 2z + 17.
(b) Distribution of the negative 3 and then combining like terms.
−3(z2 − 4z − 3) + (z2 + z)
=−3z2 + 12z + 9 + z2 + z
=(−3z2 + z2) + (12z + z) + 9
=−2z2 + 13z + 9.
Products of polynomials are found by using the associative, distributive, and exponent properties.
Example 3
Multiply the polynomials
(a) 5V(2V − 3)
(b) (t + 3)(2t2 – t + 1)
(c) (3I − 5)(I + 2)(I + 1)
Solution
(a) 5V(2V − 3) = 5V(2V) − 5V(3) = 10V2 − 15V
(b) (t + 3)(2t2 − t + 1) = t(2t2 – t + 1) + 3(2t2 – t + 1) = (2t3 − t2 + 1) + (6t2 − 3t + 3)
=2t3 + 5t2 − 2t + 3
(c) (3I − 5)(I + 2)(I + 1)
=(3I − 5)[(I + 2)(I + 1)]
=(3I − 5)[I2 + 3I + 2]
=3I[I2 + 3I + 2] − 5[I2 + 3I + 2]
=3I3 + 9I2 + 6I − 5I2 − 15I − 10
=3I3 + 4I2 − 9I − 10
The division of two polynomials can be found using long division, similar to the long division of whole numbers.
Example 4
Divide 2x3 + 3x2 + x + 6 by x2 − 1
Solution
So
![]()
Note that, (Quotient) (Divisor) + Remainder = Dividend.
2.2. Exercises
Perform the indicated algebraic operations.
1. (−V2 − 5V + 1) + (2V2 + 6V − 1)
2. (9V3 + 3V2 − 7V) − (2V3 − 6V2 – V − 3)
3. 3(2I2 − 5I + 7) + 2(−I2 + 2I − 3)
4. −4(I2 + 5I − 1) − 2(−I2 − 3I + 6)
5. −2t(3t3 + 4t2 − 5t − 6)
6. 3t(2t1/2 − 4t2 + 3t − 5)
7. (5q + 2)(3q + 4)
8. (q − 1)(2q + 3)
9. (2r + t)2
10. (r − 2t)2
11. (2k + 1)(3k2 + 4k − 1)
12. (k − 1)(2k2 − 3k + 8)
13. (p + m + n)(3p − 4m − 2n)
14. (p + 2m − n)(p − 3m − 6n)
15. (p + 1)(2p + 3)(p − 2)
16. (4p + 5)(3p − 2)(2p − 1)
17. 
18. 
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.




