20
Risk-Adjusted Performance Measures
If you cannot measure it, then you cannot manage it.
Most comparisons of hedge funds concentrate exclusively on total return figures. They openly ignore risk measures and risk-adjusted performance and claim to care only about absolute returns. Even worse, they provide no means of establishing the extent to which good past performance has been due to chance as opposed to skill. Nevertheless, these comparisons are widely used by marketers to show that their funds are superior to the competition. A 50% return over one year sounds better than 10%. Needless to say, if the funds or indices in question exhibit different risk characteristics, naive comparisons of this nature become extremely misleading. Investors who rely solely on returns to pick a hedge fund may not be prepared for the wild ride that lies ahead. Investing is by nature a two-dimensional process based not only on returns, but also on the risks taken to achieve those returns. The two factors are, however, opposite sides of the same coin, and both should be taken into consideration in order to make sound investment decisions.201
Comparing funds that have the same risk characteristics or the same return characteristics is straightforward: at equal risk, more return is always better; at equal return, less risk is always preferable. Difficulties start when we have two or more funds with different expected returns and risks. In particular, given that a higher expected return is desirable but a higher risk is not, how should one compare a high-return, high-risk fund with another fund that has a lower return and a lower risk? The question, then, is this: on a relative scale, how much additional return is sufficient compensation for additional risk? This is precisely where risk-adjusted performance measures are helpful.202
Condensing return and risk into one useful risk-adjusted number is one of the key tasks of performance measurement. When correctly done, performance measurement reduces the rugged terrain of investment to a level playing field; it thus becomes possible to compare the performance of a given fund with other funds having similar risk characteristics, as well as with other funds having different risk characteristics. It also opens the door to the correct measurement of excess performance over a benchmark – the famous so-called “alpha”. These aspects are of prime interest to both investors and money managers, as members of the former group typically select members of the latter group on the basis of their past performance statistics, and will reward them with incentive fees calculated on the basis of their future performance.
In practice, we have a number of performance measures at our disposal that will help us to choose between risky investments.203 The list is so long that it almost seems as if each hedge fund manager can choose his own measure. How should we select just one to use in our evaluations? Or do we really need them all? Or, perhaps more importantly, can we identify which approach is best? Below we review various measures of risk-adjusted performance, describe their logic, strengths and weaknesses, and answer some key, but typically ignored, questions. As we will see, each performance measure answers a specific question; there is no all-round champion. There is, however, a performance measure for each specific goal.
Figure 20.1 Evolution of $100 invested in Fund 1 since January 1998
We illustrate our review by looking at a sample of five hedge funds over the January 1998 – May 2003 period, making no claim that the sample or the period is representative of anything in particular. The selection simply consists of funds that have very different qualitative and quantitative characteristics in different market conditions. As the names of the funds are not relevant to the exercise, they have been omitted. Instead, each is identified by a number.
Fund 1 (Figure 20.1) is a fund of hedge funds that aims at producing long-term risk-adjusted capital appreciation. It focuses on several strategies, e.g. long/short, global macro, arbitrage and managed futures. Its portfolio is diversified, with around 25 to 30 managers. The total fund size is $1 billion.
Fund 2 (Figure 20.2) invests and trades primarily in US equities, both long and short. Stock selections are opportunistic, bottom up, and are based on fundamental analysis. The portfolio is widely diversified, with 200 to 250 stocks and a maximum of 4% allocation per position, inclusive of both long and short positions. The portfolio is actively traded. The fund size is larger than $3 billion.
Fund 3 (Figure 20.3) invests primarily in US equities and bonds, both long and short. In selecting investments for the fund, the investment manager emphasizes both individual stock selection and general economic analysis. The portfolio is widely diversified, with a maximum of 2.5% allocation per position, and historically a long bias. The fund size is larger than $2 billion.
Fund 4 (Figure 20.4) is a relative value, fixed-income, arbitrage fund. The fund trades actively, with 15 to 25 different strategies (yield-curve arbitrage, options, OTC derivatives, short swaps and long corporate credit, etc). Its portfolio typically contains 50 to 100 positions, mostly from G10 countries (in fact, 90% in the US fixed income market). The fund size is $1.8 billion and the maximum leverage 20 times.
Figure 20.2 Evolution of $100 invested in Fund 2 since January 1998
Fund 5 (Figure 20.5) seeks maximum capital appreciation, mainly in the US, with the flexibility of investing internationally. Its primary asset class is equity, although it may use derivatives from time to time. The fund utilizes a bottom-up approach in security selection and does not place major bets on the direction of the market. It invests in a concentrated number of stocks, both long and short. The fund size is $120 million, the maximum leverage is two times, and the least we can say is that the manager is rather aggressive.
Figure 20.3 Evolution of $100 invested in Fund 3 since January 1998
Figure 20.4 Evolution of $100 invested in Fund 4 since January 1998
The risk and return figures differ widely between funds. For instance, it is relatively difficult to compare directly the return of Fund 5 (39.96% p.a.) with the return of Fund 1 (8.16% p.a.), because of their different volatility level (79.53% versus 9.55%). Thanks to the performance measures we review below, we will be able to do an apples-to-apples comparison (see Table 20.1).
Figure 20.5 Evolution of $100 invested in Fund 5 since January 1998
Table 20.1 Average return and volatility calculation for our five different hedge funds. All data are annualized
20.1 THE SHARPE RATIO
Devised by William Sharpe (1966), a Nobel-Prize-winning economics professor, the Sharpe ratio undoubtedly remains the most commonly used measure of risk-adjusted performance.
20.1.1 Definition and interpretation
The definition of the Sharpe ratio is remarkably simple. The Sharpe ratio measures the amount of “excess return per unit of volatility” provided by a fund. It is calculated by dividing the excess return204 of the fund by its volatility. Algebraically, we have:
where RP is the average return on portfolio P, RF is the risk-free asset, and σP is the standard deviation of returns on portfolio P. All numbers are usually expressed on an annual basis, so the Sharpe ratio itself is expressed on an annual basis.205
(20.1)
As an illustration, Table 20.2 shows the Sharpe ratios calculated for our five hedge funds. The interpretation of the Sharpe ratio is straightforward: the higher the ratio the better. A high Sharpe ratio means that the fund in question delivered a high return for its level of volatility, which is always good. In contrast, a Sharpe ratio of 1.0 indicates a return on investment that is proportional to the risk taken in achieving that return, and a Sharpe ratio lower than 1 indicates a return on investment that is less than the risk taken. In our case, over the period in question, we can see that Fund 5 was in fact better than Fund 1 because it offered a reward of 0.45% p.a. per unit of volatility, while Fund 1 only offered 0.41% p.a. However, the best fund in the group appears to be Fund 4, with a reward of 0.80% p.a. per unit of volatility – which corresponds to a Sharpe ratio of 0.80.
How can one interpret this 0.80 figure? Consider, for instance, the case of an investor who holds the risk-free asset (4.23% return, no volatility). If this investor agrees to purchase Fund 4 shares (11.36% return, 8.95% volatility), the incremental return is 7.13% (11.36% minus 4.23%) and the incremental risk is 8.95% (8.95% minus 0%). Hence, the ratio of incremental return to incremental risk is 7.13%/8.95% ≈ 0.80. In other terms, the investor is willing to accept an increase in volatility of 1% as long as this increase is rewarded by 0.80% return. This is precisely what a Sharpe ratio equal to 0.80 says.
Table 20.2 Sharpe ratio calculation for five different hedge funds. All data are annualized. The T-bill rate has an average return of 4.23% p.a. over the period
Now, if our investor decides to allocate 50% of his portfolio to Fund 4 and the rest to the risk-free asset, he would get a portfolio with a return of 7.80% and a volatility of 4.48%. Compared to the risk-free asset, the incremental return is 3.57%, the incremental risk is 4.48%, and the Sharpe ratio is still 0.80. And if our investor decides to allocate 150% of his portfolio to Fund 4 and finance the extra 50% position by borrowing at the risk-free rate, he would get a portfolio with a return of 14.93% and a volatility of 13.43%. Compared to the risk-free asset, the incremental return is 10.70%, the incremental risk is 13.43%, and the Sharpe ratio is again 0.80. This clearly shows that the Sharpe ratio of a fund is not influenced by its leverage. All leveraged and unleveraged versions of Fund 4, and more generally, all leveraged and unleveraged versions of any portfolio, will have the same Sharpe ratio.
Figure 20.6 Risk/return trade-off achievable by leveraging (solid line) or deleveraging (dotted line) Fund 4. It shows that all combinations of Fund 4 and the risk – free asset generate higher returns at the same level of risk than any combination of another fund and the risk-free asset
Graphically, in a mean return/volatility space, the Sharpe ratio is the slope of the line joining the risk-free asset to the fund being examined – see Figure 20.6. The equation of this line can be expressed as:
Return = Risk-free rate + (Sharpe ratio × Volatility)
That is, in the case of Fund 4,
Return = 4.23% + (0.80 × Volatility).
The financial literature often refers to this line as the capital allocation line.206 Each point on this line corresponds to a particular allocation between the risk-free asset and Fund 4. Stated differently, any portfolio on this line can be created by leveraging or deleveraging Fund 4. It is clear from Figure 20.6 that any other fund combined with the T-bills will never reach the capital allocation line of Fund 4.
20.1.2 The Sharpe ratio as a long/short position
More recently, Sharpe (1994) revised the definition of the Sharpe ratio and suggested a new interpretation in terms of differential return with respect to a benchmark. Let RP and RB be the average returns on a fund P and on a benchmark portfolio B respectively. The differential return between the fund and its benchmark is defined as (RP − RB). From a financial perspective, these differential returns correspond to a zero investment strategy that consists in going long on the fund in question and short on the benchmark. Alternatively, one could also swap the return on the benchmark for the return on the fund, and vice versa.
The revised Sharpe ratio – also called the information ratio – compares the average differential return with its volatility. The latter is nothing more than the tracking error of the fund P with respect to the benchmark B. Algebraically: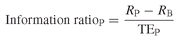
(20.2)
When the benchmark equals the risk-free rate, the information ratio equals the traditional Sharpe ratio.
The beauty of this new definition is that it allows for a more general interpretation. Let us consider the benchmark as a hypothetical initial investment and let us try to select an asset that improves on the benchmark in risk-expected return terms. In this framework, a higher information ratio represents a better departure from the benchmark because it implies an expected return larger than the return for relatively little extra risk – see Figure 20.7. Hence, we should always pick the asset that has the highest information ratio.
20.1.3 The statistics of Sharpe ratios
Most of the time, Sharpe ratios are measured and reported without any information about their statistical significance. Once again, this is regrettable. The building blocks of the Sharpe ratio – expected/average excess returns and volatility/tracking error-are unknown quantities that must be estimated statistically from a sample of returns. They are therefore subject to estimation error, which implies that the Sharpe ratio itself is also subject to estimation error.207 Thus, we should always verify the statistical significance of Sharpe ratio estimates before stating any conclusion about the performance of a fund.
Figure 20.7 Illustration of the revised Sharpe ratio. Fund A provides a better departure from the benchmark than Fund B
The financial literature describes several approaches to dealing with the uncertainty surrounding Sharpe ratios.
• The first approach is the Jobson and Korkie (1981) test for the equality of the Sharpe ratios of any two portfolios (Box 20.1). It is the first formal test of the significance of performance, but it requires normality of asset returns, which is often not the case for individual hedge funds.
• The second approach is the Gibbons et al. (1989) test to verify ex-ante portfolio efficiency (Box 20.2). Although there is a substantial theoretical difference between the two concepts of portfolio performance and portfolio efficiency, there is a close relationship between them. In particular, the test shows whether the adjunction of new assets in a universe effectively results in a significant improvement of performance, by comparing the maximum Sharpe ratios obtained for the original universe with those for the augmented universe. This test has often been applied in the literature, for instance to examine the ex-ante efficiency of portfolios, to test the benefits of adding international investments to a domestic portfolio, or to compare equally weighted with optimized portfolios – see, for instance, Rubens et al. (1998) or Cheng and Liang (2000).
• Finally, the third approach is that described recently by Lo (2002). Although still at its early stages, this line of research is the most promising. It derives the statistical distribution of the Sharpe ratio using standard econometric methods. The derivation is made under several different sets of assumptions for the statistical behaviour of the return series on which the Sharpe ratio is based-e.g. mean reversion, momentum, and other forms of serial correlation. Lo finds that all these effects can have a non-trivial impact on the Sharpe ratio estimator itself. For instance, positive serial correlation can yield annualized Sharpe ratios that are overstated by more than 65%, therefore resulting in inconsistent rankings.
Whatever the approach, it is crucial that performance is investigated over a sufficiently long period of time. Without a minimum sample size, determining portfolio performance becomes a hazardous task, and it is difficult to really assess whether performance was due to luck or skill-or lack of it.
Box 20.1 The Jobson and Korkie test statistic
The Jobson and Korkie (1981) test statistic can be formulated as follows. Let μ1 and μ2 be the mean excess returns of the portfolios under investigation, σ1 and σ2 the return volatility of the two portfolios, and σ1, 2 the covariance of the two portfolio returns. The excess returns are assumed to be serially independent and normally and independently distributed.
Jobson and Korkie use the following Z statistic:
where θ is the asymptotic variance of the expression in the numerator, calculated follows208:
Jobson and Korkie show that the Z statistic is approximately normally distributed, with a zero mean and a unit standard deviation for large samples under the null assumption that the two Sharpe ratios are equal.
(20.3)
(20.4)
A significant Z statistic would reject the null hypothesis of equal risk-adjusted performance and would suggest that one of the investment portfolio strategies outperforms the other. However, Jobson and Korkie note that the statistical power of the test is low, especially for small sample sizes. As illustrated by Jorion (1985), at a 5% significance level, the test fails to reject a false null hypothesis up to 85% of the time. Thus, a statistically significant Z between two portfolios can be seen as strong evidence of a difference in risk-adjusted performance.
Box 20.2 The Gibbons, Ross and Shanken test
The Gibbons, et al. (1989) test compares the estimated maximum Sharpe ratio for the original universe (denoted Sharpe1 ) with the estimated maximum Sharpe ratio for the augmented universe (denoted Sharpe2). The authors show that the statistic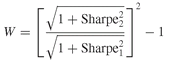
follows a Wishart distribution, which is a generalization of the χ 2 distribution. Under the null hypothesis that the Sharpe ratio of the extended universe is not different from the Sharpe ratio of the original universe, the statistic W should not be statistically different from zero. Since increasing the number of assets in a universe can only improve the maximum Sharpe ratio, we are only concerned with positive values of W. Any large positive deviation from zero implies that the two Sharpe ratios are actually different.
(20.5)
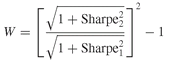
Working with a Wishart distribution is not so convenient. Fortunately, a simple transformation suggested by Morrison (1976) shows that the statistic
has a central F-distribution with (N, T − N − 1) degrees of freedom, where T is the number of returns observed and N is the number of assets in the original universe. As with any F-statistic, N must be low in relation to T for the test to have good discriminatory power.
(20.6)
20.2 THE TREYNOR RATIO AND JENSEN ALPHA
Two other widely used performance measures are the Treynor ratio and the Jensen alpha (frequently simply called “alpha”). Both find their roots in financial theory, more specifically in the Capital Asset Pricing Model (CAPM) developed by Sharpe (1964).
20.2.1 The CAPM
Centrepiece of modern financial economics, the CAPM was originally developed to (i) explain the rationale for diversification, (ii) provide a theoretical structure for the pricing of assets with uncertain returns in a competitive market and (iii) explain the differences in risk premiums across assets. A rigorous exposition of the CAPM principles and results is far beyond the scope of this book and may easily be found in the literature.209 In the following paragraphs, therefore, we limit ourselves to recalling briefly the intuition behind the CAPM, listing its major conclusions, and then proceeding directly to their implications in terms of performance measurement.
The fundamental premise of the CAPM is that the volatility of an asset can be split into two parts: a systematic risk and a specific risk. The systematic risk part is the risk of being affected by general market movements. It represents the part of an asset’s volatility that is perfectly positively or negatively correlated with the market. The specific risk, on the other hand, is specific to each asset. It represents the remaining part of an asset’s volatility that is not correlated with the market.
When investors form portfolios, the systematic risk parts of individual assets are simply added up to give the systematic risk of the whole portfolio. This risk is non-diversifiable and will be present in all portfolios. The specific risk parts do not add up, however, but rather tend to compensate each other, particularly when the assets considered are negatively correlated. This is the impact of diversification. Hence, in a well-diversified portfolio, each asset’s specific risk should be eliminated by diversification, so that the total portfolio’s specific risk should be insignificant.
The second premise of the CAPM is that risk-averse and rational investors do not want to subject themselves to a risk that can be diversified away. Rather, they attempt to optimally construct their portfolios from uncorrelated assets in order to eliminate specific risk. As a consequence, investors should not care about the total volatility of individual assets, but only about the systematic risk component – the only risk that remains in the final portfolio.
The logical consequence of the foregoing is that there should be no reward for non-systematic risk. Although measurable at the individual asset level, specific risk will disappear at the portfolio level. So why would the market ever reward something that does not exist any more in a well-diversified portfolio? At equilibrium, investors should only be rewarded for the systematic risk they take, not for the non-systematic risk they have eliminated. This is precisely what the CAPM says.
The CAPM asserts that the expected return on a given asset should be equal to the risk-free interest rate plus a risk premium. The latter depends linearly on the market risk exposure (i.e. the beta of the asset) and the market risk premium (i.e. what the market portfolio pays above the risk-free rate for taking market risk). Therefore, the expected return on a risky asset should be given by:
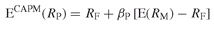where RP and RM are respectively the percentage returns on the portfolio P and on the market portfolio M, RF denotes the risk-free rate, βP is the beta of portfolio P with respect to the market portfolio M, and E() denotes the unconditional expectation operator.
Equation (20.7) is the most important conclusion derived from the CAPM. It states that expected returns are linearly related to market risk (beta), but not, as often believed, to total risk (volatility). Other things being equal, a high beta asset should produce a higher expected return than the market and a low beta asset should produce a lower return. Similarly, increasing the market risk premium should increase the return of all assets with positive beta. In that respect, one could say that the CAPM philosophy is the exact opposite of traditional stock picking, as its attempts to understand the market as a whole rather than look at what makes each investment opportunity unique.
Note that equation (20.7) can easily be rewritten in terms of risk premiums by simply subtracting the risk-free rate from both sides of the security market line (SML) equation. This yields
Graphically, in a return-beta space, the CAPM implies that all fairly priced securities and portfolios should plot along a line. This line is the SML (Figure 20.8). Its intercept with the
vertical axis should be the risk-free rate, and its slope should be equal to the market risk premium. The more risk-averse investors are, the steeper the slope and the higher the expected return for a given level of systematic risk.
(20.8)
Figure 20.8 The security market line (SML)
By construction, the risk-free asset and the market portfolio should fall exactly on the SML, with betas of 0 and 1 respectively. Consequently, any asset on the SML can be “replicated” by an appropriate mix of the risk-free asset and the market. This property – called the two-fund separation theorem – is particularly useful in creating a passive benchmark, when assessing the performance of an actively managed portfolio.
20.2.2 The market model
The CAPM and its graphical equivalent, the SML, give predictions about the expected relationship between risk and return. Theoretically, they should only be interpreted strictly as ex-ante predictive models. However, when doing performance analysis, the framework is different. Performance must be assessed ex-post, based on a sample of observed past data. What we need then is an explanatory model, and the ex-ante CAPM must be transformed into an ex-post testable relationship. The latter usually takes the form of a time series regression of excess returns of individual assets on the excess returns of some aggregate market index. It is called the market model (Figure 20.9), and can be written as:
where Ri and RM are the realized returns on security i and the market index, respectively, αi is the expected firm-specific return and εi is the unexpected firm-specific return. If the CAPM holds and if markets are efficient, αi should not be statistically different from zero, and εi should have a mean of zero. The coefficients αi and βi correspond to the slope and the intercept of the regression line.
Figure 20.9 The market model
As we will see shortly, this equation constitutes the source of two major performance measures of financial portfolios, namely, Jensen’s alpha (1968) and the Treynor ratio (1965).
Most practitioners tend to confuse the CAPM with time series regression. Although the two models look similar, they are fundamentally different. The market model is just an ad hoc, convenient, single-factor model fitted to observed data, while the CAPM is an economic equilibrium model. Furthermore, the market model uses a simple market index as a proxy for the entire (non-observable) market portfolio of the CAPM.
An interesting interpretation of the market model is given by rearranging the terms in equation (20.9) to obtain:
The terms (1 − βi ) and βi can be interpreted as weights in a portfolio. Thus, equation (20.11) means that the return on a portfolio is made up of four components: (i) an asset-specific expected return αi ; (ii) an allocation to the risk-free asset; (iii) an allocation to the market portfolio; and (iv) an error term, which on average should be zero.
Several commercial firms provide estimates of beta but their data should be treated with caution. These firms often ignore the risk-free rate as well as dividends, and simply estimate betas by regressing the returns on stocks against the return on the market:
This shortcut generally has no practical impact on the estimate of beta, but the corresponding alpha is useless for performance evaluation, as it differs significantly from the original alpha.
(20.12)
20.2.3 The Jensen alpha
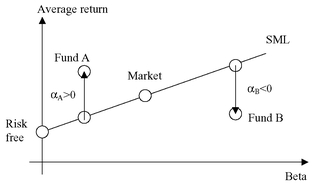
According to the CAPM, it is impossible for an asset to remain located above or below the security market line (SML). If an asset produces a return that is higher than it should be for its beta, then investors will rush in to buy it and drive up its price, lowering the return and returning it to the SML. If the asset is located below the SML, then investors will hurry to sell it, driving down the price and hence increasing the return. Consequently, if all assets are fairly priced, deviations from the SML should not occur, or at least should not last very long.
Nevertheless, active fund managers are typically in search of assets that deviate from the SML. They attempt to identify them before the market reacts, so that they can profit from the mispricing. If they are successful, they will achieve a return that is above what could be expected, given the market risk taken. Hence, their portfolios will also be located above the SML. Conversely, unsuccessful managers will achieve a return that is lower than what could be expected, given the market risk taken. Hence, their portfolios will be located below the SML. This suggests a straightforward way of measuring performance, namely, the Jensen alpha, named after Harvard professor Michael Jensen (1968).
The Jensen alpha is defined as the difference between the realized return and the return predicted by the CAPM:
(20.13)
Figure 20.10 Undervalued and overvalued securities with the SML
That is,
(20.14)
Hence, the Jensen alpha is measured as the difference between the effectively realized risk premium and the expected risk premium. According to the CAPM, only market risk should be rewarded, so the alpha should be nil. If this is not the case, the alpha can be interpreted as an indicator of superior performance when it is positive or of poor performance when it is negative.
Graphically, a security with an alpha of zero will plot on the SML. A security with a positive alpha (e.g. Fund A in Figure 20.10) will plot above the SML. It generates more return than it should, given its systematic risk (measured by beta). A security with a negative alpha (e.g. Fund B in Figure 20.10) will plot below the SML. It generates less return than it should, given its systematic risk (measured by beta).
The Jensen measure can also be interpreted as the profitability of a net arbitrage position that goes long on the evaluated fund and goes short on both the risk-free asset and the market in proportions that neutralize market risk. For example, consider a fund with a beta of 0.6. Then Jensen’s alpha measures the average profit of investing $1 in the fund, obtaining the funds from borrowing $0.40 (shorting the risk-free asset) and shorting $0.60 worth of the market portfolio. If the alpha is positive, that means that an investor who initially holds a portfolio made up of $0.60 worth of the market portfolio and $0.40 of the risk-free asset can improve his portfolio by diverting a small fraction of his wealth to the fund in question. If the alpha is negative, the investor should avoid the fund.210
When confronted with several funds, the alpha decision rule is of course to choose the investment that maximizes the value added-that is, the investment with the highest alpha. We will therefore prefer investment A over B if αA > αB. As an illustration, Table 20.3 shows the Jensen alpha calculations for our five hedge funds. Note that the alpha is calculated from monthly returns, so that it is itself a monthly figure. Clearly, according to the Jensen alpha, (Box 20.3), Fund 5 dominates the sample.
Table 20.3 Jensen alpha calculation for five different hedge funds
20.2.4 The Treynor (1965) ratio
In the market model, the value added (or withdrawn) by a manager is measured by the alpha, while the market risk exposure is measured by the beta. Jack L. Treynor, one of the fathers of modern portfolio theory and former editor of The Financial Analysts Journal, suggested comparing the two quantities:
(20.16)
Replacing αP by its definition and simplifying gives
(20.17)
All returns are usually expressed on an annual basis, so the Treynor ratio itself is expressed on an annual basis. The risk-free asset is often specified as Treasury bills, and beta is often measured against a diversified market index (e.g. S&P 500). Note that the derivations implicitly assume βP ≠ 0.
In a sense, the Treynor ratio is a reward-to-risk ratio similar to the Sharpe ratio. The key difference is that it looks at systematic risk only, not total risk. Higher values of the Treynorratio are always desirable as they indicate greater return per unit of (market) risk. As an illustration,
Box 20.3 Jensen’s alpha
It is possible to derive a precise interpretation of Jensen’s alpha in terms of optimal portfolio choice by relating it to the Sharpe ratio. Suppose an investor initially holds a combination of an index portfolio tracking the market and the risk-free asset, in proportions wM and 1 − wM). This investor considers whether he should add fund P to his portfolio. In other words, he considers whether he should take a small fraction wP of his wealth and invest it in portfolio P, while reducing the fractions held in the risk-free asset and the index to (1 − wP)(1 − wM) and (1 − wP)wM respectively.
It can then be shown that the derivative (in the financial calculus sense) of the Sharpe ratio of the resulting portfolio with respect to ε, evaluated at wP = 0 (no investment yet), is
(20.15)
Table 20.4 Treynor ratio calculation for five different hedge funds. The T-bill rate has an average return of 4.23% p.a. over the period
Table 20.4 displays the Treynor ratios obtained for our five hedge funds. We observe once again that Fund 4 seems to dominate the sample, with a Treynor ratio equal to 113.02, thanks to its relatively low beta (0.06).
20.2.5 Statistical significance
Once again, a crucial element in the Jensen alpha and Treynor ratio is the question of statistical significance. In particular, the quality of the regression used to obtain the beta coefficient should be scrutinized. First, are the coefficients statistically different from zero? Second, how high is the explanatory power of the regression? As an illustration, consider Figure 20.5, which displays a statistic called the R-square. Roughly stated, the R-square (R2) measures the quality of the regression model used to calculate the Jensen alpha and the Treynor ratio.
We saw previously that Fund 4 seems to dominate the sample with a Treynor ratio equal to 113.02, thanks to its relatively low beta (0.06). However, we now see that the R2 of the regression that provided this beta is only 0.02. This implies that the S&P 500 behaviour only explains 2% of the variance of Fund 4. Do we feel confident in basing our conclusions on a model that has such a low explanatory power? Not likely! Hence, we should be cautious and always assess the quality of our models before accepting their conclusions.
20.2.6 Comparing Sharpe, Treynor and Jensen
Investors frequently wonder why there are differences between the fund rankings provided by the Sharpe ratio, the Treynor ratio and the Jensen alpha. The three measures are indeed different. On the one hand, both the Treynor ratio and the Jensen alpha issue from the CAPM and measure risk the same way. However, the Treynor ratio provides more information than Jensen’s alpha. In particular, two securities with different risk levels that provide the same excess returns over the same period will have the same alpha but will differ with respect to the Treynor ratio. The difference comes from the fact that the Treynor ratio provides the performance of the portfolio per unit of systematic risk. On the other hand, the Sharpe ratio focuses on a different type of risk – total risk, as opposed to systematic risk. It penalizes funds that have a high volatility and therefore funds that have non-systematic risk. Hence, in general, the ranking of Sharpe ratios will usually be different from that of Treynor ratios or Jensen alphas. Intuitively, it is only when applied to well-diversified traditional portfolios that the three measures will result in similar rankings because most of the risk will be systematic. In the case of hedge funds, the non-systematic component is usually large, so very different rankings may be obtained.
Table 20.5 Statistical significance of the market model coefficients
It is relatively easy to derive the exact conditions that must hold for the Sharpe ratio and the Treynor ratio to provide the same ranking. Consider two funds, A and B, such that fund A has a higher Treynor ratio than fund B. That is,
(20.18)
Replacing the betas with their definitions and rearranging terms, we find that
where ρi,M denotes the correlation between fund i and the market. Therefore, the Treynor ratio will provide the same ranking as the Sharpe ratio only for assets that have identical correlations to the market.
(20.19)
Similarly, we can derive the conditions that must hold for the Sharpe ratio and the Jensen alpha to provide the same ranking. Consider two funds, A and B, such that fund A has a higher alpha than fund B. That is,
(20.20)
Replacing the alphas with their definitions and rearranging terms yields
(20.21)
Hence, the Treynor ratio will provide the same ranking as the Sharpe ratio only for assets that have identical correlations to the market and the same volatility. Most of the time, this condition will not be encountered so the rankings will be different.
Another frequent question from investors is: “Which measure should be used to evaluate portfolio performance?” The simple answer is: “It depends.” To evaluate an entire portfolio, the Sharpe ratio is appropriate. It is simple to calculate, does not require a beta estimate and penalizes the portfolio for being non-diversified. To evaluate securities or funds for possible inclusion in a broader or master portfolio, either the Treynor ratio or Jensen’s alpha is appropriate. However, they require a beta estimate and assume that the master portfolio is well diversified.
20.2.7 Generalizing the Jensen alpha and the Treynor ratio
As we will see, the market model is one of the simplest asset pricing models possible. It expresses everything in terms of a single factor, the market portfolio. However, one can easily extend the market model, for instance, by including additional factors or by postulating some non-linear relationships. In this case, alpha will be defined as the difference between the realized return and the new model-predicted return.
A particular and unfortunate case of what precedes is the tendency of some investment practitioners to use the term “alpha” to describe the extent to which a portfolio’s returns have exceeded expectations, or simply to measure returns in excess of those over a benchmark index (e.g. S&P 500). In a CAPM framework, this implicitly assumes that the beta of the considered portfolio is in fact equal to 1, which is often not verified.
In the context of multi-factor models the Treynor ratio has also been generalized by Hübner (2003). Conceptually, the Generalized Treynor ratio is defined as the abnormal return of a portfolio per unit of weighted-average systematic risk. In a linear multi-index, these requirements are fulfilled by normalizing the risk premia using a benchmark portfolio and by rotating the factors to obtain an orthonormed hyperplane for risk dimensions. This performance measure is invariant to the specification of the asset pricing model, the number of factors or the scale of the measure.
20.3 M2, M3 AND GRAHAM-HARVEY
More recently, several researchers have provided new perspectives on measuring portfolio performance. Although not yet as popular as the Sharpe ratio or Jensen’s alpha, these measures are gaining ground in the hedge fund industry.
20.3.1 The M2 performance measure
Despite near universal acceptance among academics and institutional investors, the Sharpe ratio is too complicated for the average investor. The reason is that it expresses performance as an excess return per unit of volatility, while most investors are used to dealing with absolute returns. This motivated Leah Modigliani from Morgan Stanley and her grandfather, the Nobel Prize winner Franco Modigliani, to develop and suggest a replacement for the Sharpe ratio.211 The new performance measure, called M2 after the names of its founders, expresses performance directly as a return figure, which should ease its comprehension.
The key idea of the M2 performance measure is to adjust all funds by leveraging or deleveraging them using the risk-free asset, so that they all have the same volatility – typically the market volatility. Say, for instance, that we want to compare the performance of a fund (named P) with the performance of the market (named M). In general, we observe that σP ≠ σM, so that we cannot compare the two assets by just looking at their returns. According to M2, we need to form a portfolio P* composed of the original fund P and T-bills (with return RF and no volatility) that has the same standard deviation as M. Then, one can simply compare the adjusted funds and the market solely on the basis of the return.
There are two possible situations. If the fund has a higher volatility than the market (σP > σM), then portfolio P* will contain a mix of T-bills and the original fund P. This is the de-leveraging situation illustrated in Figure 20.11. In this case, we have:
(20.22)
Solving for RP∗ yields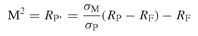
(20.23)
Figure 20.11 The M2 performance measure when the fund has a higher volatility than the market (σP > σM). The adjusted portfolio P* is a mix of T-bills and P
If the fund has a lower volatility than the market (σP < σM), then portfolio P* will contain a short position in T-bills and a long position in the original fund P. This is the leveraging situation illustrated in Figure 20.12. In this case,
(20.24)
Solving for RP∗ yields
(20.25)
In both cases, the resulting portfolio P* is compared with the market solely on the basis of return. In essence, for a fund P with a given risk and return, the M2 measure is equivalent to the return the fund would have achieved if it had the same risk as the market. Thus, the fund with the highest M2 will have the highest return for any level of risk – very much like the fund with the highest Sharpe ratio.
Figure 20.12 The M2 performance measure when the fund has a lower volatility than the market (σP < σM). The adjusted portfolio P* is made up of portfolio P and a loan at the risk-free rate
Table 20.6 Calculating M2 for our sample of hedge funds
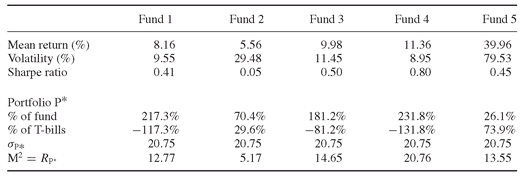
As an illustration, Table 20.6 shows the calculation of M2 for our sample of five funds. The benchmark volatility level was set at 20.75%, which corresponds to the S&P 500 volatility over the period in question. The T-bill rate has an average return of 4.23% p.a. over the period. The ranking we obtain with M2 is the same as the ranking of the Sharpe ratio. This confirms that the M2 performance measure is essentially a new variant of the Sharpe ratio. It is just easier to interpret, because it is expressed directly in terms of return.
It is worth noting that any reference point other than the volatility of the market could equally well be chosen. With M2, the market simply provides a standard risk level to which all portfolios are scaled so that they can be compared “apples to apples”. The economic significance of the market, if any, is left aside.
Arun Muralidhar from J.P. Morgan Investment Management argues that M2 is not a sufficient rule for making decisions on how to rank funds or structure portfolios. It is true that M2 accounts for differences in standard deviations between a portfolio and a benchmark, but not for the differences in correlation. He therefore suggests a new performance measure called M3 that corrects for the difference in correlations. Although interesting from a theoretical perspective, M3 has never really been applied in practice.
20.3.2 GH1 and GH2
In parallel with Modigliani and Modigliani, John Graham and Campbell Harvey have developed two simple approaches to adjust the risk of compared portfolios in order to end up with the same volatility. Both of them are also based on a leveraging/deleveraging approach.
The first approach suggested by Graham and Harvey consists in leveraging or deleveraging the market to match the volatility of the fund examined. The performance measure GH1 is then defined as the difference between the mean fund return and the mean return on the volatility-matched portfolio. Figure 20.13 details the geometry of the measure applied to two funds. Combining the S&P 500 with Treasury bills to match the volatility of Fund A yields a portfolio with a higher return than Fund A. Hence, GH1 for fund A is negative, which indicates underperformance. In contrast, leveraging the S&P 500 to match the volatility of Fund B yields a portfolio with a lower return than Fund B. Hence, GH1 for fund B is positive, which indicates outperformance.
Figure 20.13 Interpreting GH1 by leveraging or unleveraging the S&P 500
The second approach suggested by Graham and Harvey consists in leveraging or deleveraging the fund examined to match the volatility of the market. The performance measure GH2 is then defined as the difference between the mean return on the volatility-matched portfolio and the mean market return. Figure 20.14 details the geometry of the measure applied to the same two funds. Leveraging Fund A with Treasury bills to match the volatility of the market yields a portfolio with a lower return than the market. Hence, GH2 for fund A is negative, which indicates underperformance. In contrast, combining Fund A with Treasury bills to match the volatility of the market yields a portfolio with a higher return than the market. Hence, GH2 for fund B is positive, indicating outperformance.
Figure 20.14 Interpreting GH2 by leveraging or unleveraging the analysed funds
The sets of portfolios obtained by mixing T-bills and other assets form curves rather than straight lines. This is because Graham and Harvey reject the usual assumption that the T-bill return has zero variance and zero covariance with the portfolio being evaluated. In reality, the usual assumption does hold if the maturity of the T-bills coincides exactly with the evaluation period. That is, the cash is effectively a zero-coupon instrument maturing exactly at the end of the evaluation period. In practice, though, this is often not the case, and there is likely to be a non-zero correlation between the interest rate changes and asset returns, which gives the curve. Depending on the level of correlation, this could lead to misleading inferences about the performance, particularly for low volatility funds where substantial leverage is needed to achieve the market volatility. However, the impact is generally negligible for well-diversified portfolios.
The two Graham and Harvey measures look very similar but in fact they provide different perspectives.
• GH1 is similar to the Jensen alpha measure, except that, with Jensen, the benchmark portfolio (beta times the market index) has the same market exposure (beta) as the analysed portfolio, but not necessarily the same total volatility.212
• GH2 is similar to the M2 measure, but does not rely on the assumption of zero risk for the cash proxy.
20.4 PERFORMANCE MEASURES BASED ON DOWNSIDE RISK
Dissatisfaction with the variance as a risk measure, coupled with other behavioural evidence, has led some researchers to propose alternative risk-adjusted performance measures. Several of these are based on the downside risk approach – see, for instance, Sortino and van der Meer (1991), Fishburn (1977), Sortino and Price (1994) Marmer and Ng (1993) or Merriken (1994).
20.4.1 The Sortino ratio
Frank Sortino, Director of the Pension Research Institute and a professor emeritus at San Francisco State University, reconsidered the issue of performance measurement from the perspective of downside risk. His contention was that the most important risk was not volatility, but rather the risk of not achieving the return in relation to an investment goal. Hence, he suggested replacing the Sharpe ratio by the Sortino ratio, which measures the incremental return over a minimum acceptable return (MAR) divided by the downside deviation (as opposed to standard deviation) below the MAR.
Table 20.7 Sortino ratio calculations for our five different hedge funds. All data are annualized
Algebraically, we have:
where RP and MAR are respectively the average percentage returns on portfolio P and a minimum acceptable return, and DDP is the downside deviation of returns of portfolio P below the MAR. All numbers are usually expressed on an annual basis, so the Sortino ratio is annualized.
(20.26)
As an illustration, Table 20.7 shows the Sortino ratios of our five funds calculated with respect to different minimum acceptable returns. If the goal of the investor is to avoid losing money, the MAR is set at zero and Fund 4 ranks as the best fund. If the goal of the investor is to achieve at least the risk-free rate, the MAR is set equal to the T-bill rate and Fund 5 comes out on top. Finally, if we use the mean return of each fund as the reference MAR, Fund 1 becomes the best performing fund.
Clearly, the Sortino ratio can accommodate different degrees of target returns. However, there are different downside deviations for different minimum acceptable rates and hence different Sortino ratios and different rankings of the funds under consideration. It is therefore essential to specify the minimum acceptable rate used to calculate any Sortino ratio, as well to use the same rate for different funds in order to be able to perform comparisons.
20.4.2 The upside potential ratio
Instead of searching for the manager who had the highest average return over some period of time, some, if not most, investors would prefer to find those managers who had the highest average returns above their MAR. Hence, Sortino, van der Meer and Plantinga (1999a, 1999b) suggested replacing the excess return used in the denominator of the Sortino ratio by the upside potential. The latter is defined as the expected return in excess of the MAR and can be thought of as the potential for success. The ratio of the upside potential to the downside risk is termed the “upside potential ratio”.
Table 20.8 Upside potential ratio calculations for our five different hedge funds. All data are annualized
An important advantage of using the upside potential ratio rather than the Sortino ratio is the consistency in the use of the reference rate for evaluating both profits and losses. An upside potential ratio of 1.6, for instance, means that the fund has 60% more upside potential than downside risk, where the term “risk” refers to the same concept.
As an illustration, Table 20.8 shows the upside potential ratios of our five funds calculated with respect to different minimum acceptable returns. If the goal of the investor is to avoid losing money, the MAR is set at zero and Fund 3 ranks as the best fund. If the goal of the investor is to achieve at least the risk-free rate, the MAR is set equal to the T-bill rate and Fund 5 comes out on top. Finally, if we use the mean return of each fund as the reference MAR, Fund 1 becomes the best performing fund.
20.4.3 The Sterling and Burke ratios
The Sterling and Burke ratios are widely advertised by commodity trading advisers, because those ratios illustrate what they believe they do best: namely, let their profits ride and stringently cap their losses.
The Sterling ratio goes one step further than the Sortino ratio by looking at the drawdowns to measure risk. It is defined as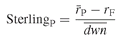
where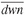 
is the average of the most significant drawdowns during the observation period. What is meant by a “significant” drawdown remains to be defined. Some analysts use the maximum drawdown rather than the average drawdown.
(20.27)
is the average of the most significant drawdowns during the observation period. What is meant by a “significant” drawdown remains to be defined. Some analysts use the maximum drawdown rather than the average drawdown.Burke (1994) proposed using the square root of the sum of the squares of each drawdown, in order to penalize deep extended drawdowns as opposed to numerous mild ones. The Burke ratio is defined as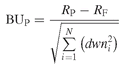
(20.28)
20.4.4 Return on VaR (RoVaR)
Another measure that is popular particularly among practitioners is the return on value at risk, or RoVaR (Box 20.4). This is defined simply as the return on the portfolio (RP) divided by the absolute213 value at risk (VaRP).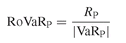
(20.29)
Box 20.4 Return on Value at Risk (RoVaR)
In the case of normally distributed returns, it is relatively easy to express the RoVaR of a portfolio as a function of the Sharpe ratio, as the VaR typically depends on the mean return (RP) and on the volatility of the portfolio (σP). More precisely,
where -k is the standard normal variable reflecting the confidence level on which the VaR is predicated (for example, k = −1.645 if we have a 95% confidence level). It follows that:
VaRP = — (RP + kσP)
Using equation (20.1) to replace RP, we obtain
This shows that there is a link between the RoVaR and the Sharpe ratio. It also evidences that we should not expect the same ranking of funds from both measures. As an illustration, if the risk-free rate RF is zero, we have: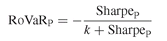
As k can take any value, there is no reason for the RoVaR and the Sharpe ratio to provide equal rankings.
Table 20.9 RoVaR ratio calculations for our five different hedge funds. All data are annualized
As in the case of the Sortino ratio, the RoVaR ratio can be customized to cater for different holding periods as well as different level of confidence for the VaR. As an illustration, Table 20.9 shows the RoVaR of our five funds using a one-month historical value at risk calculated at 99% and at 95% confidence. Once again, the ranking differs, because the risk definitions are different.
20.5 CONCLUSIONS
Over the last few decades, a number of sophisticated measures have been developed to monitor the risk-adjusted performance of hedge funds. These measures have much in common as regards their underlying framework and financial intuition, but they rely on different calculation techniques and parameters. Hence, when applied to a series of hedge funds, they often produce different rankings.
From the performance evaluator’s point of view, this array of performance measures offers a rich choice but at the same time makes the selection of a method difficult – if at all possible. Not surprisingly, for some years, unscrupulous product marketers have taken advantage of this difficulty. They simply considered hedge fund performance measurement as a game, following one guiding principle: “Give me a fund and I will find the performance measure and the time period that makes it look attractive.”
Today, hedge fund investing is no longer a game but a serious business. Each investor embarking on a hedge fund investment has his own strategic rationale and critical objectives, which will define his perception of risk. Hence, rather than waiting for all the pieces of the puzzle to fall into place, he should carefully assess his current situation in order to be proactive in his choice of a performance measure. Only by knowing what he is looking for can he identify the performance measure that best suits his requirements. Then, and only then, will the historical analysis of portfolio performance provide much more than just good marketing information (see Box 20.5).
Box 20.5 The danger of using historical data to model uncertainty
At this point, we should stress that one needs to be cautious when analysing hedge funds for a future investment on the basis on their historical track record. Whatever the risk measure selected, history may sometimes be misleading, particularly for hedge funds that agree to be systematically exposed to a catastrophic risk and regularly pocket the associated risk premium. Until the Big Event materializes, such funds are likely to generate a low-volatility positive stream of returns, and any empirical measure will evidence them as being great investments. History looks great, but reality is that the underlying extreme risks are often excessively large and should deter most investors. As an illustration, consider a hedge fund that is guaranteed to make money 98% of the time with very limited average losses. Would you be interested? It is likely. Now, what if the fund’s trading strategy turned out to be the following. Take a card in a 52 card deck. If the ace of spades comes up, you lose 52 million dollars; otherwise, you earn a million dollars. On average, you will lose $19,231 each time you play, but you will win 51 out of 52 hands. This is what is known as a negatively skewed trading strategy – although as long as losses did not occur, it is not really skewed.
To avoid such cases, the historical track record of hedge funds should always be analysed from a qualitative and quantitative perspective to understand the underlying risk factors, as well as the magnitude of the losses that could occur if an undesirable event-risk ever materialized.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.