So far, we have been mostly using a set of formal systems to prove software correctness. In this final chapter, we show how to both create and use a formal system in order to be able to prove facts. For that, we will provide a minimal implementation1 of propositional logic, as described in Chapter 2. For a more advanced implementation of a formal system, see [7].
The syntax of the
formal system expressed in BNF (Backus-Naur form) is
1 prop ::= P | Q | R | unop prop | prop brelop prop
2 unop ::= "!"
3 brelop ::= "&&" | "||" | "->"
The
code in Dafny, which follows the same syntax:
1 datatype Prop =
2 P | Q | R
3 | Not (Prop)
4 | And (Prop, Prop)
5 | Or (Prop, Prop)
6 | Imp (Prop, Prop)
We now have a way to represent some logical formulas, for example,
? ∧
? as
And(P, Q). In Dafny, we get construction of well-formed formulas for free due to algebraic data structures. In some untyped programming languages, such as
Python, we could use hashmaps to simulate the types.
1 # Python
2 def And(x, y):
3 return {'x': x, 'y': y, 'type': 'and'}
4
5 def Imp(x, y):
6 return {'x': x, 'y': y, 'type': 'imp'}
Further, in our implementation, we also need a way to differentiate between well-formed formulas and theorems since not all well-formed formulas are theorems. For that, we provide the
Proof data
type and a way to extract a proof:
1 //datatype Prop = ...
2 datatype Proof<T> = Proof(T)
3 function method FromProof(x : Proof<Prop>) : Prop
4 {
5 match x {
6 case Proof(a) => a
7 }
8 }
Note that
Proof(And(P, Q)) (⊢
? ∧
?) is different from
And(P, Q) (
? ∧
?). Here’s how we can construct and destruct (extract) proofs
in Python:
1 # Python
2 def Proof(x):
3 return {'v': x, 'type': 'proof'}
4 def FromProof(x):
5 if not isinstance(x, dict) or not 'v' in x: return None
6 return x['v']
Note in the Python code how we have to be extra careful with the conditional checks, whereas in Dafny, it is much simpler due to pattern matching.
The
Proof constructor mustn’t be used directly; proofs should only be constructed given the rules that we provide next.
1 function method RuleJoin(x : Proof<Prop>, y : Proof<Prop>) :
Proof<Prop>
2 {
3 Proof(And(FromProof(x), FromProof(y)))
4 }
5 function method RuleSepL(x : Proof<Prop>) : Proof<Prop>
6 {
7 match FromProof(x) {
8 case And(a, b) => Proof(a)
9 case x => Proof(x)
10 }
11 }
The preceding implementation corresponds to the following
rules:
These rules come from GEB [1], and we list all of them here for completeness:
Joining Rule (And-introduction): If ? and ? are theorems, then ? ∧ ? is a theorem.
Sep Rule (And-elimination): If ? ∧ ? is a theorem, then both ? and ? are theorems.
Fantasy Rule (Implication-introduction): If ? were a theorem, ? would be a theorem (? → ?).
Contrapositive Rule: ? → ? and ¬? → ¬? are interchangeable.
De Morgan’s Rule: ¬? ∧ ¬? and ¬(? ∨ ?) are interchangeable.
Double-Tilde Rule (Double negation): The string ¬¬ can be deleted from any theorem. It can also be inserted into any theorem.
Rule of Detachment (Implication-elimination): If ? and ? → ? are both theorems, then ? is a theorem.
Switcheroo Rule: ? ∨ ? and ¬? → ? are interchangeable.
The most powerful
rule is the
Fantasy Rule, implemented as follows:
1 function method RuleFantasy(x : Prop, y : (Proof<Prop> ->
Proof<Prop>)) : Proof<Prop>
2 {
3 Proof(Imp(x, FromProof(y(Proof(x)))))
4 }
RuleFantasy accepts a non-proven term x : Prop, whereas other rules accept proven terms; the hypothesis needn’t be necessarily true, it only states that “If this hypothesis were a theorem, then that would be a theorem.” The second argument is a function y : (Proof<Prop> -> Proof<Prop>) that accepts a Proof and returns a Proof, basically another rule that will be used to transform the hypothesis x. As a result, it produces the theorem ? → y(?).
Here’s the same implementation of the previous rules in
Python:
1 # Python
2 def RuleJoin(x, y):
3 if not isinstance(x, dict) or not isinstance(y, dict) or
not 'type' in x or not 'type' in y or x['type'] !=
'proof' or y['type'] != 'proof': return None
4 return Proof(And(FromProof(x), FromProof(y)))
5 def RuleSepL(x):
6 if not isinstance(x, dict) or not 'type' in x or x['type']
!= 'proof': return None
7 wff = FromProof(x)
8 if wff['type'] == 'and': return Proof(wff['x'])
9 return Proof(wff)
10 def RuleFantasy(x, y):
11 if not isinstance(x, dict) or not 'type' in x or not
callable(y): return None
12 return Proof(Imp(x, FromProof(y(Proof(x)))))
For most rules, we can write intro (
RuleJoin) and elim (
RuleSepL) functions. Here’s another example of a rule that performs interchanging of formulas:
1 function method RuleDeMorgan(x : Proof<Prop>) : Proof<Prop>
2 {
3 match FromProof(x) {
4 case And(Not(a), Not(b)) => Proof(Not(Or(a, b)))
5 case Not(Or(a, b)) => Proof(And(Not(a), Not(b)))
6 case x => Proof(x)
7 }
8 }
Since we defined the rules in Dafny as
function method, we can build proofs iteratively by printing the results. For example, we can prove that ⊢
? ∧
? →
? ∧
? as follows:
1 method Main()
2 {
3 var p_and_q := And(P, Q);
4 var join := (x) => RuleJoin(RuleSepL(x), RuleSepL(x));
5 var x := RuleFantasy(p_and_q, join);
6 print(x);
7 assert x == Proof(Imp(p_and_q, And(P, P)));
8 }
9 // Or simply
10 method Example()
11 ensures RuleFantasy(And(P, Q), (x) => RuleJoin(RuleSepL(x),
RuleSepL(x))) == Proof(Imp(And(P, Q), And(P, P)))
12 {}
Note how we embedded a formal system (propositional logic) within a formal system (Dafny/Python), and we were able to reason about it through symbolic manipulation; in Dafny, this corresponds to pattern matching and data types, whereas in Python, it corresponds to conditionals and hashmaps.
 Exercise 1 Implement the remainder of the rules in Dafny or your favorite programming language.
Exercise 1 Implement the remainder of the rules in Dafny or your favorite programming language.
 Exercise 2 Using the rules you implemented in the previous exercise, prove the following fact in the system: ¬¬(¬? → ?) → ? ∨ ?.
Exercise 2 Using the rules you implemented in the previous exercise, prove the following fact in the system: ¬¬(¬? → ?) → ? ∨ ?.
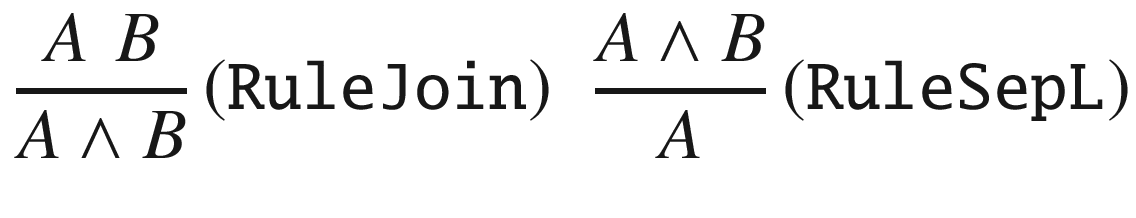
![]() Exercise 1 Implement the remainder of the rules in Dafny or your favorite programming language.
Exercise 1 Implement the remainder of the rules in Dafny or your favorite programming language.![]() Exercise 2 Using the rules you implemented in the previous exercise, prove the following fact in the system: ¬¬(¬? → ?) → ? ∨ ?.
Exercise 2 Using the rules you implemented in the previous exercise, prove the following fact in the system: ¬¬(¬? → ?) → ? ∨ ?.