Chapter 8
Modular Lattices
8.1 INTRODUCTION
We describe a special class of lattices called modular lattices. Modular lattices are numerous in mathematics; for example, the lattice of normal subgroups of a group is modular, the lattice of ideals of a ring is modular, and so is the finite-dimensional vector space lattice. Distributive lattices are a special class of modular lattices. The set of all consistent global states in a distributed computation forms a distributive lattice and is therefore a modular lattice.
In this chapter, we first introduce both modular and distributive lattices to show the relationship between them. Later, we focus on modular lattices. Distributive lattices are considered in detail in Chapter 9.
8.2 MODULAR LATTICE
The definition says that if ![]() , then one can bracket the expression
, then one can bracket the expression ![]() either way.
either way.
We will show that all distributive lattices are modular. Recall that a lattice ![]() is distributive if
is distributive if ![]() .
.
In this definition, the equality can be replaced by ![]() because of the following observation.
because of the following observation.
A similar observation applies to the definition of modular lattices as shown by the following lemma.
We can now show the relationship between the modularity condition and the distributivity condition for lattices.
8.3 CHARACTERIZATION OF MODULAR LATTICES
We now give examples of lattices that are not modular or modular but not distributive. All lattices of four elements or less are modular. The smallest lattice which is not modular is the pentagon (![]() ) shown in Figure 1.4(a). In this lattice,
) shown in Figure 1.4(a). In this lattice, ![]() holds; however,
holds; however, ![]() , whereas
, whereas ![]() .
.
The diamond lattice (![]() ) shown in Figure 1.4(b) is modular but not distributive. To see this, note that in the diagram of
) shown in Figure 1.4(b) is modular but not distributive. To see this, note that in the diagram of ![]() we have
we have
![]()
and ![]() .
.
Since ![]() ,
, ![]() is not distributive.
is not distributive.
We now focus on modular lattices and list some theorems that characterize modular lattices.
In the definition of modular lattices, if ![]() satisfies
satisfies ![]() , then we get that
, then we get that ![]() . The following theorem shows that to check modularity it is sufficient to consider
. The following theorem shows that to check modularity it is sufficient to consider ![]() 's that are in the interval
's that are in the interval ![]() .
.
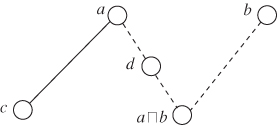
Figure 8.1 Proof of Theorem 8.5.
The following lemma is useful in proving the Pentagon theorem, which gives a characterization of modular lattices using the absence of a sublattice isomorphic to a pentagon (or ![]() ).
).
We are now ready for another characterization of modular lattices due to R. Dedekind.
Modular lattices can also be characterized using an identity on lattices. An advantage of a characterization based on identities is that it allows easy manipulation of expressions: the left-hand side of any identity can be replaced by the right-hand side.
Consider two incomparable elements ![]() as shown in Figure 8.2. Define two intervals
as shown in Figure 8.2. Define two intervals ![]() , and
, and ![]() . We can define maps
. We can define maps ![]() and
and ![]() from one interval to the other as follows.
from one interval to the other as follows.
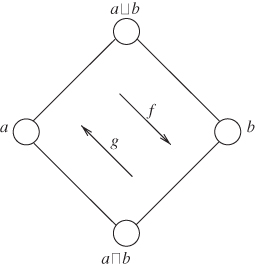
Figure 8.2 Theorem 8.9.
We now give yet another characterization of modular lattices using upper and lower covering conditions.
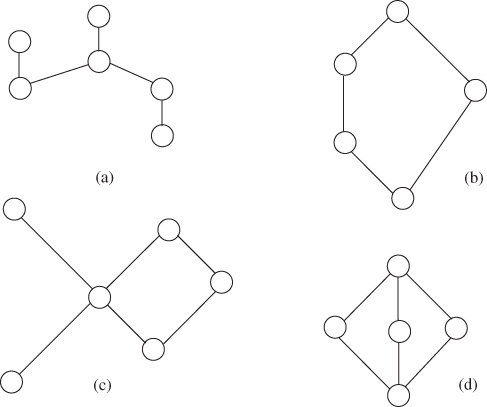
Figure 8.3 (a) A ranked poset, (b) A poset that is not ranked, (c) A ranked and graded poset, and (d) A ranked and graded lattice.
We now define a ranked poset and a graded poset. Some examples are shown in Figure 8.3.
8.4 PROBLEMS
- 8.1. Show that if
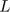 is a graded lattice, then
is a graded lattice, then
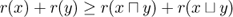 is equivalent to the Upper Covering Condition.
is equivalent to the Upper Covering Condition.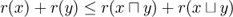 is equivalent to the Lower Covering Condition.
is equivalent to the Lower Covering Condition.
- 8.2. Complete the proof of Theorem 8.5.
- 8.3. Show the shearing identity for modular lattices.
[Shearing Identity] A lattice
 is modular iff
is modular iff 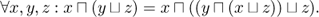
- 8.4. Complete the proof of Theorem 8.9.
- 8.5. Prove Theorem 8.11.
- 8.6. Prove Theorem 8.14.
8.5 BIBLIOGRAPHIC REMARKS
The book by Gratzer [Grä71, Grä03] contains most of the results in this chapter except for our emphasis on calculational proofs.
