7
Stochastic differential equations
7.1 Existence and uniqueness theorem and main proprieties of the solution
Let ![]() be a complete probability space and
be a complete probability space and ![]() a standard Wiener process defined on it. Let
a standard Wiener process defined on it. Let ![]() be a non‐anticipative filtration. Let
be a non‐anticipative filtration. Let ![]() be a
be a ![]() ‐measurable r.v. (therefore independent of the Wiener process); in particular, it can be a deterministic constant. Having defined in Chapter the Itô stochastic integrals, the stochastic integral equation
‐measurable r.v. (therefore independent of the Wiener process); in particular, it can be a deterministic constant. Having defined in Chapter the Itô stochastic integrals, the stochastic integral equation
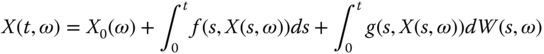
does have a meaning for ![]() if, as in Definition 6.4 of an Itô process,
if, as in Definition 6.4 of an Itô process,

Of course we need to impose appropriate conditions on ![]() and
and ![]() to insure that
to insure that ![]() and
and ![]() , so that the integral form 7.1 has meaning and so the corresponding (Itô) stochastic differential equation (SDE)
, so that the integral form 7.1 has meaning and so the corresponding (Itô) stochastic differential equation (SDE)
also has a meaning for ![]() .
.
Besides having a meaning, we also want the SDE 7.2 to have a unique solution and this may require appropriate conditions for ![]() and
and ![]() . Like ordinary differential equations (ODEs), a restriction on the growth of these functions will avoid explosions of the solution (i.e. avoid the solution to diverge to
. Like ordinary differential equations (ODEs), a restriction on the growth of these functions will avoid explosions of the solution (i.e. avoid the solution to diverge to ![]() in finite time) and a Lipschitz condition will insure uniqueness of the solution.
in finite time) and a Lipschitz condition will insure uniqueness of the solution.
We will denote by ![]() the set of real‐valued functions
the set of real‐valued functions ![]() with domain
with domain ![]() that are Borel‐measurable jointly in
that are Borel‐measurable jointly in ![]() and
and ![]() 1 and, for some
1 and, for some ![]() and all
and all ![]() and
and ![]() , verify the two properties:
, verify the two properties:
 (Lipschitz condition)
(Lipschitz condition)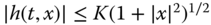 (restriction on growth).
(restriction on growth).
We will follow the usual convention of not making explicit the dependence of random variables and stochastic processes on chance ![]() , but one should keep always in mind that such dependence exists and so the Wiener process and the solutions of SDE do depend on
, but one should keep always in mind that such dependence exists and so the Wiener process and the solutions of SDE do depend on ![]() .
.
We now state an existence and uniqueness theorem for SDEs which is, with small nuances, the one commonly shown in the literature. Note that the conditions stated in the theorem are sufficient (not necessary), so there may be some improvements (i.e. the class ![]() of functions for which existence and uniqueness is insured may be enlarged), particularly in special cases. We will talk about that later.
of functions for which existence and uniqueness is insured may be enlarged), particularly in special cases. We will talk about that later.
Of course the starting time was labelled 0 and we will work on a time interval ![]() just for convenience, but nothing prevents one from working on intervals like
just for convenience, but nothing prevents one from working on intervals like ![]() .
.
Although further complications arise in the stochastic case, the theorem and the proof are inspired on an analogous existence and uniqueness theorem for ODEs. Both use the technique of proving uniqueness by assuming two solutions and showing they must be identical. Both use the constructive Picard's iterative method of approximating the solution by feeding one approximation into the integral equation to get the next approximation:

This method, which is very convenient for the proof, can be used in practice to approximate the solution, although it is quite slow compared to other available methods.
Monte Carlo simulation of SDEs
Although a more complete treatment will be presented in Section 12.2, we mention here some ideas on how to simulate trajectories of the solution of an SDE.
If an explicit expression for the solution of the SDE can be obtained, it can be used to simulate trajectories of ![]() . If the explicit expression only involves the Wiener process directly at the present time, we can simulate the Wiener process by the method of Section 4.1 and plug the values into the expression, as we will do to simulate the solution of the Black–Scholes model in Section 8.1. Monte Carlo simulation for more complicated explicit expressions will be addressed in Section 12.2
.
. If the explicit expression only involves the Wiener process directly at the present time, we can simulate the Wiener process by the method of Section 4.1 and plug the values into the expression, as we will do to simulate the solution of the Black–Scholes model in Section 8.1. Monte Carlo simulation for more complicated explicit expressions will be addressed in Section 12.2
.
Unfortunately, in many cases we are unable to obtain an explicit expression, in which case the trajectories can be simulated using an approximation of ![]() obtained by discretizing time. One uses a partition
obtained by discretizing time. One uses a partition ![]() of
of ![]() with a sufficiently large
with a sufficiently large ![]() to reduce the numerical error. Typically, but not necessarily, the partition points are equidistant, with
to reduce the numerical error. Typically, but not necessarily, the partition points are equidistant, with ![]() . A trajectory is simulated iteratively at the partition points. One starts (step 0) simulating
. A trajectory is simulated iteratively at the partition points. One starts (step 0) simulating ![]() by using the distribution of
by using the distribution of ![]() ; if
; if ![]() is a deterministic value, then
is a deterministic value, then ![]() and no simulation is required. At each iteration (step
and no simulation is required. At each iteration (step ![]() with
with ![]() ), one uses the previously simulated value
), one uses the previously simulated value ![]() to simulate the next value
to simulate the next value ![]() . The simplest method to do that is the Euler method, the same as is used for ODEs. In the context of SDEs, it is also known as the Euler–Maruyama method. In this method,
. The simplest method to do that is the Euler method, the same as is used for ODEs. In the context of SDEs, it is also known as the Euler–Maruyama method. In this method, ![]() and
and ![]() are approximated in the interval
are approximated in the interval ![]() by constants, namely by the values they take at the beginning point of the interval (to ensure the non‐antecipative property of the Itô calculus). This leads to the first‐order approximation scheme
by constants, namely by the values they take at the beginning point of the interval (to ensure the non‐antecipative property of the Itô calculus). This leads to the first‐order approximation scheme

Since the approximate value of ![]() is known from the previous iteration, the only thing random in the above scheme is the increment
is known from the previous iteration, the only thing random in the above scheme is the increment ![]() . The increments
. The increments ![]() (
(![]() ) are easily simulated (we have done this in Section 4.1
when simulating trajectories of the Wiener process), since they are independent random variables having a normal distribution with mean zero and variance
) are easily simulated (we have done this in Section 4.1
when simulating trajectories of the Wiener process), since they are independent random variables having a normal distribution with mean zero and variance ![]() . At the end of the iterations, we have the approximate values at the time partition points of a simulated trajectory. Of course, this iterative procedure can be repeated to produce other trajectories.
. At the end of the iterations, we have the approximate values at the time partition points of a simulated trajectory. Of course, this iterative procedure can be repeated to produce other trajectories.
There are faster methods (i.e. requiring not so large values of ![]() ), like the Milstein method. On the numerical resolution/simulation of SDE, we refer the reader to Kloeden and Platen (1992), Kloeden et al. (1994), Bouleau and Lépingle (1994), and Iacus (2008).
), like the Milstein method. On the numerical resolution/simulation of SDE, we refer the reader to Kloeden and Platen (1992), Kloeden et al. (1994), Bouleau and Lépingle (1994), and Iacus (2008).
SDE existence and uniqueness theorem
7.2 Proof of the existence and uniqueness theorem
We now present a proof of the existence and uniqueness Theorem 7.1, which can be skipped by non‐interested readers. Certain parts of the proof are presented in a sketchy way; for more details, the reader can consult, for instance, Arnold (1974), Øksendal (2003), Gard (1988), Schuss (1980) or Wong and Hajek (1985).
(a) Proof of uniqueness
Let ![]() and
and ![]() be two a.s. continuous solutions. They satisfy 7.4
and so are non‐anticipative (only depend on past values of themselves and of the Wiener process). Since
be two a.s. continuous solutions. They satisfy 7.4
and so are non‐anticipative (only depend on past values of themselves and of the Wiener process). Since ![]() and
and ![]() are Borel measurable functions,
are Borel measurable functions, ![]() ,
, ![]() ,
, ![]() and
and ![]() are non‐anticipative. We could work with
are non‐anticipative. We could work with ![]() , but we have not yet proved that such second‐order moment indeed exists. So we replace it by the truncated moment
, but we have not yet proved that such second‐order moment indeed exists. So we replace it by the truncated moment ![]() , with
, with ![]() if
if ![]() and
and ![]() for all
for all ![]() and
and ![]() otherwise. Note that
otherwise. Note that ![]() is non‐anticipative, that
is non‐anticipative, that ![]() , and that
, and that ![]() for
for ![]() . Since
. Since ![]() and
and ![]() satisfy 7.4
, using the inequality
satisfy 7.4
, using the inequality ![]() , one gets
, one gets

Using the Schwarz inequality (which, in particular, implies ![]()
![]() ), the fact that
), the fact that ![]() , and the norm preservation property for Itô integrals of
, and the norm preservation property for Itô integrals of ![]() functions, one gets
functions, one gets
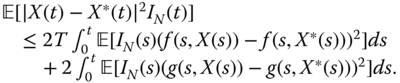
Putting ![]() and using the Lipschitz condition, one has
and using the Lipschitz condition, one has

Using the Bellman–Gronwall lemma,4 also known as Gronwall's inequality, one gets ![]() , which implies
, which implies ![]() a.s. But
a.s. But
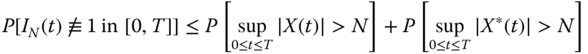
and since ![]() are
are ![]() are a.s. bounded in
are a.s. bounded in ![]() (due to their a.s. continuity), both probabilities on the right‐hand side become arbitrarily small for every sufficiently large
(due to their a.s. continuity), both probabilities on the right‐hand side become arbitrarily small for every sufficiently large ![]() . So,
. So, ![]() a.s. for
a.s. for ![]() , and so also for all
, and so also for all ![]() (since the set of rational numbers
(since the set of rational numbers ![]() is countable). Due to the continuity, we have a.s.
is countable). Due to the continuity, we have a.s. ![]() for all
for all ![]() and therefore
and therefore ![]() a.s.
a.s.
(b) Proof of existence
The proof of existence is based on the same Picard's method that is used on a similar proof for ODEs. It is an iterative method of successive approximations, starting with
and using the iteration
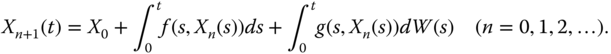
We just need to prove that ![]() (
(![]() ) are a.s. continuous functions and that this sequence uniformly converges a.s. The limit will then be a.s. a continuous function, which, as we will show, is the solution of the SDE.
) are a.s. continuous functions and that this sequence uniformly converges a.s. The limit will then be a.s. a continuous function, which, as we will show, is the solution of the SDE.
Since ![]() , we have
, we have ![]() and will see by induction that
and will see by induction that ![]() and
and ![]() for all
for all ![]() . In fact, assuming this is true for
. In fact, assuming this is true for ![]() , we show it is true for
, we show it is true for ![]() because (due to the restriction on growth, the norm preservation of the Itô integral, the inequality
because (due to the restriction on growth, the norm preservation of the Itô integral, the inequality ![]() , and the Schwarz's inequality), with
, and the Schwarz's inequality), with ![]() ,
,

Using a reasoning similar to the one used in the proof of 7.6, but now with no need to used truncated moments (since the non‐truncated moments exist), one obtains
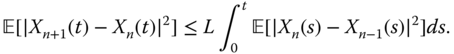
Iterating 7.10, one obtains by induction

Using the restriction on growth, one obtains

and so
Since

using (6.27) and the Lipschitz condition, one gets

By Thebyshev inequality,

By the Borel–Cantelli lemma,
and so, for every sufficiently large ![]() ,
, ![]() a.s. Since the series
a.s. Since the series ![]() is convergent, the series
is convergent, the series ![]() converges uniformly a.s. on
converges uniformly a.s. on ![]() (notice that the terms are bounded by
(notice that the terms are bounded by ![]() ). Therefore
). Therefore
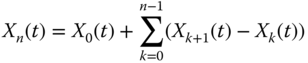
converges uniformly a.s. on ![]() .
.
This shows the a.s. uniform convergence of ![]() on
on ![]() as
as ![]() . Denote the limit by
. Denote the limit by ![]() . Since
. Since ![]() are obviously non‐anticipative, the same happens to
are obviously non‐anticipative, the same happens to ![]() . The a.s. continuity of the
. The a.s. continuity of the ![]() and the uniform convergence imply the a.s. continuity of
and the uniform convergence imply the a.s. continuity of ![]() . Obviously, from the restriction on growth and a.s. continuity of
. Obviously, from the restriction on growth and a.s. continuity of ![]() , we have
, we have ![]() a.s. and
a.s. and ![]() a.s. Consequently,
a.s. Consequently, ![]() is an Itô process and the integrals in 7.4
make sense.
is an Itô process and the integrals in 7.4
make sense.
The only thing missing is to show that ![]() is indeed a solution, i.e. that
is indeed a solution, i.e. that ![]() satisfies 7.4
for
satisfies 7.4
for ![]() . Apply limits in probability to both sides of 7.8. The left side
. Apply limits in probability to both sides of 7.8. The left side ![]() converges in probability to
converges in probability to ![]() (the convergence is even a stronger a.s. uniform convergence). On the right‐hand side, we have:
(the convergence is even a stronger a.s. uniform convergence). On the right‐hand side, we have:
- The integrals
 converge a.s., and so converge in probability to
converge a.s., and so converge in probability to 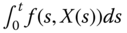 . In fact,
. In fact,  a.s. (due to the Lipschitz condition).
a.s. (due to the Lipschitz condition). - The integrals
 converge to
converge to  in probability. In fact, the Lipschitz condition implies
in probability. In fact, the Lipschitz condition implies  a.s. and we can use the result of Exercise 6.9 in Section 6.4.
a.s. and we can use the result of Exercise 6.9 in Section 6.4. - So, the right‐hand side

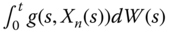 converges in probability to
converges in probability to 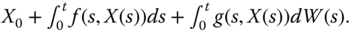
Since the limits in probability are a.s. unique, we have

i.e. ![]() satisfies 7.4
.
satisfies 7.4
.
Proof that ![]() and
and ![]()
From 7.9, putting ![]() gives
gives ![]() . Iterating, we have
. Iterating, we have

and therefore ![]() . Letting
. Letting ![]() , by the dominated convergence theorem, we get
, by the dominated convergence theorem, we get
Consequently, ![]() and
and ![]() .
.
Proof that ![]() and
and ![]() are in
are in ![]()
From the previous result, ![]() and
and ![]() , and so
, and so ![]() and
and ![]() are in
are in ![]() .
.
As a consequence, the stochastic integral ![]() is a martingale.
is a martingale.
Proof of 7.5
By the Itô formula (6.37),
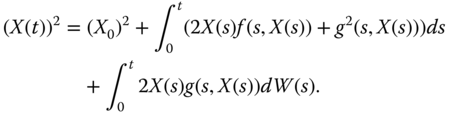
Applying mathematical expectations, one gets
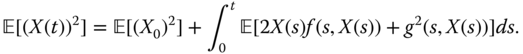
We have assumed that the stochastic integral has a null expected value, although we have not shown that the integrand function was in ![]() . Since this may fail, we should, in good rigour, have truncated
. Since this may fail, we should, in good rigour, have truncated ![]() by
by ![]() (to ensure the nullity of expectation of the stochastic integral) and then go to the limit as
(to ensure the nullity of expectation of the stochastic integral) and then go to the limit as ![]() .
.
Using the restriction on growth and the inequality ![]() , one gets
, one gets

Put ![]() and
and ![]() , note that
, note that ![]() and apply Gronwall's inequality to obtain
and apply Gronwall's inequality to obtain ![]() , and so the first inequality of 7.5
.
, and so the first inequality of 7.5
.
From 7.4 , squaring and applying mathematical expectations, one gets

Applying the first expression of 7.5
and bounding the ![]() that shows up in the integral by
that shows up in the integral by ![]() , one gets the second expression in 7.5
.
, one gets the second expression in 7.5
.
Proof that the solution is m.s. continuous
For ![]() ,
, ![]() is also solution of
is also solution of ![]()
![]() . Since now the initial condition is the value
. Since now the initial condition is the value ![]() at time
at time ![]() and the length of the time interval is
and the length of the time interval is ![]() , the second inequality in 7.5
now reads
, the second inequality in 7.5
now reads

and we can now use the first inequality of 7.5
to bound ![]() by
by ![]() . We conclude that
. We conclude that ![]() as
as ![]() , which proves the m.s. continuity.
, which proves the m.s. continuity.
Proof of the semigroup property: For ![]() ,
, ![]()
This is an easy consequence of the trivial property of integrals (if one splits the integration interval into two subintervals, the integral over the interval is the sum of the integrals over the subintervals), which gives ![]() .
.
Proof that the solution is a Markov process
Let ![]() . The intuitive justification that
. The intuitive justification that ![]() is a Markov process comes from the semigroup property
is a Markov process comes from the semigroup property ![]() . This means that
. This means that ![]() can be obtained in the interval
can be obtained in the interval ![]() as solution of
as solution of ![]() . So, given
. So, given ![]() ,
, ![]() is defined in terms of
is defined in terms of ![]() and
and ![]() (
(![]() ), and so is measurable with respect to
), and so is measurable with respect to ![]() . Since
. Since ![]() is
is ![]() ‐measurable, and so is independent of
‐measurable, and so is independent of ![]() , we conclude that, given
, we conclude that, given ![]() ,
, ![]() only depends on
only depends on ![]() . Since
. Since ![]() is independent of
is independent of ![]() , also
, also ![]() (future value) given
(future value) given ![]() (present value) is independent of
(present value) is independent of ![]() (past values). Thus, it is a Markov process.
(past values). Thus, it is a Markov process.
A formal proof can been seen, for instance, in Gihman and Skorohod (1972), Arnold (1974), and Gard (1988).
Proof that, if ![]() and
and ![]() are also continuous in
are also continuous in ![]() , then
, then ![]() is a diffusion process
is a diffusion process
Let ![]() and
and ![]() . Conditioning on
. Conditioning on ![]() (deterministic initial condition), from 7.13 we obtain
(deterministic initial condition), from 7.13 we obtain
First of all, let us note that expressions similar to 7.5
can be obtained for higher even ![]() ‐order moments if
‐order moments if ![]() . Therefore, since now the initial condition
. Therefore, since now the initial condition ![]() is deterministic and so has moments of any order
is deterministic and so has moments of any order ![]() , we can use such expressions to obtain expressions of higher order similar to 7.14. We get
, we can use such expressions to obtain expressions of higher order similar to 7.14. We get
with ![]() and
and ![]() appropriate positive constants. Given
appropriate positive constants. Given ![]() , since
, since ![]() , we get
, we get
Due to 7.15, these moments exist for all ![]() (even for odd
(even for odd ![]() , the moment exists since the moment of order
, the moment exists since the moment of order ![]() exists). Since
exists). Since ![]() is a Markov process with a.s. continuous trajectories, we just need to show that (5.1), (5.2), and (5.3) hold.
is a Markov process with a.s. continuous trajectories, we just need to show that (5.1), (5.2), and (5.3) hold.
Due to the Lipschitz condition, notice that ![]() and
and ![]() are also continuous functions of
are also continuous functions of ![]() .
.
From 7.15
with ![]() we get
we get ![]() , with
, with ![]() constant, so that
constant, so that ![]() as
as ![]() Therefore
Therefore
So, (5.1) holds.
Starting from 7.4 , since the Itô integral has zero expectation, we get

We also have, using the Lipschitz condition, Schwarz's inequality, and 7.14 ,

where ![]() is a positive constant that does not depend on
is a positive constant that does not depend on ![]() . The continuity of
. The continuity of ![]() in
in ![]() holds on the close interval
holds on the close interval ![]() and is uniform. Therefore, given an arbitrary
and is uniform. Therefore, given an arbitrary ![]() , there is a
, there is a ![]() independent of
independent of ![]() such that
such that

From 7.16, 7.17, and 7.18, we obtain (5.2) with ![]() .
.
To obtain (5.3) with ![]() , one starts from 7.12 instead of 7.4
, using also as initial condition
, one starts from 7.12 instead of 7.4
, using also as initial condition ![]() and applying similar techniques.
and applying similar techniques.
This concludes the proof of Theorem 7.1. ![]()
7.3 Observations and extensions to the existence and uniqueness theorem
The condition ![]() (i.e.
(i.e. ![]() has finite variance) is really not required and we could prove Theorem 7.1, with the exception of parts (c) and (d), without making that assumption. Of course, for parts (c) and (d) we would need the assumption, since otherwise the required second‐order moments of
has finite variance) is really not required and we could prove Theorem 7.1, with the exception of parts (c) and (d), without making that assumption. Of course, for parts (c) and (d) we would need the assumption, since otherwise the required second‐order moments of ![]() might not exist.
might not exist.
In fact, except for parts (c) and (d), we could easily adapt the proof presented in Section 7.2 in order to wave that assumption. We would just replace ![]() by its truncation to an interval
by its truncation to an interval ![]() . Since the truncated r.v. is in
. Since the truncated r.v. is in ![]() , the proof would stand for the truncated
, the proof would stand for the truncated ![]() , and then we would go to the limit as
, and then we would go to the limit as ![]() .
.
The restriction to growth and the Lipschitz condition for ![]() and
and ![]() do not always need to hold for all points
do not always need to hold for all points ![]() , or
, or ![]() and
and ![]() . In the case where the solution
. In the case where the solution ![]() of the SDE has values that always belong to a set
of the SDE has values that always belong to a set ![]() , then it is sufficient that the restriction on growth and the Lipschitz conditions are valid on
, then it is sufficient that the restriction on growth and the Lipschitz conditions are valid on ![]() . In fact, in that case nothing changes if we replace
. In fact, in that case nothing changes if we replace ![]() and
and ![]() by other functions that coincide with them on
by other functions that coincide with them on ![]() and have zero values out of
and have zero values out of ![]() , and these other functions satisfy the restriction on growth and the Lipschitz condition.
, and these other functions satisfy the restriction on growth and the Lipschitz condition.
For existence and uniqueness, we could use a weaker local Lipschitz condition for ![]() and
and ![]() instead of the global Lipschitz condition we have assumed in Theorem 7.1.
instead of the global Lipschitz condition we have assumed in Theorem 7.1.
A function ![]() with domain
with domain ![]() satisfies a local Lipschitz condition if, for any
satisfies a local Lipschitz condition if, for any ![]() , there is a
, there is a ![]() such that, for all
such that, for all ![]() and
and ![]() ,
, ![]() , we have
, we have
The proof of existence uses a truncation of ![]() to the interval
to the interval ![]() and ends by taking limits as
and ends by taking limits as ![]() .
.
Consider ![]() and
and ![]() fixed. We can say that the SDE
fixed. We can say that the SDE ![]() ,
, ![]() , or the corresponding stochastic integral equation
, or the corresponding stochastic integral equation ![]() , is a map (or transformation) that, given a r.v.
, is a map (or transformation) that, given a r.v. ![]() and a Wiener process
and a Wiener process ![]() (on a certain given probability space endowed with a non‐anticipative filtration
(on a certain given probability space endowed with a non‐anticipative filtration ![]() ), transforms them into the a.s. unique solution
), transforms them into the a.s. unique solution ![]() of the SDE, which is adapted to the filtration. If we choose a different Wiener process, the solution changes. This type of solution, which is the one we have studied so far, is the one that is understood by default (i.e. if nothing in contrary is said). It is called a strong solution. Of course, once the Wiener process is chosen, the solution is unique a.s. and to each
of the SDE, which is adapted to the filtration. If we choose a different Wiener process, the solution changes. This type of solution, which is the one we have studied so far, is the one that is understood by default (i.e. if nothing in contrary is said). It is called a strong solution. Of course, once the Wiener process is chosen, the solution is unique a.s. and to each ![]() there corresponds the value of
there corresponds the value of ![]() and the whole trajectory
and the whole trajectory ![]() of the Wiener process, which the SDE (or the corresponding stochastic integral equation) transforms into the trajectory
of the Wiener process, which the SDE (or the corresponding stochastic integral equation) transforms into the trajectory ![]() of the SDE solution. In summary,
of the SDE solution. In summary, ![]() and the Wiener process are both given and we seek the associated unique solution of the SDE.
and the Wiener process are both given and we seek the associated unique solution of the SDE.
There are also weak solutions. Again, consider ![]() and
and ![]() fixed. Now, however, only
fixed. Now, however, only ![]() is given, not the Wiener process. What we seek now is to find a probability space and a pair of processes
is given, not the Wiener process. What we seek now is to find a probability space and a pair of processes ![]() and
and ![]() on that space such that
on that space such that ![]() ; of course, these are not unique. The difference is that, in the strong solution, the Wiener process is given a priori and chosen freely, the solution being dependent on the chosen Wiener process, while in the weak solution, the Wiener process is obtained a posteriori and is part of the solution.5 Of course, a strong solution is also a weak solution, but the reverse may fail. One can see a counter‐example in Øksendal (2003), in which the SDE has no strong solutions but does have weak solutions.
; of course, these are not unique. The difference is that, in the strong solution, the Wiener process is given a priori and chosen freely, the solution being dependent on the chosen Wiener process, while in the weak solution, the Wiener process is obtained a posteriori and is part of the solution.5 Of course, a strong solution is also a weak solution, but the reverse may fail. One can see a counter‐example in Øksendal (2003), in which the SDE has no strong solutions but does have weak solutions.
The uniqueness considered in Theorem 7.1 is the so‐called strong uniqueness, i.e. given two solutions, their sample paths coincide for all ![]() with probability one. We also have weak uniqueness, which means that, given two solutions (no matter if they are weak or strong solutions), they have the same finite‐dimensional distributions. Of course, strong uniqueness implies weak uniqueness, but the reverse may fail. Under the conditions assumed in the existence and uniqueness Theorem 7.1, two weak or strong solutions are weakly unique. In fact, given two solutions, either strong or weak, they are also weak solutions. Let them be
with probability one. We also have weak uniqueness, which means that, given two solutions (no matter if they are weak or strong solutions), they have the same finite‐dimensional distributions. Of course, strong uniqueness implies weak uniqueness, but the reverse may fail. Under the conditions assumed in the existence and uniqueness Theorem 7.1, two weak or strong solutions are weakly unique. In fact, given two solutions, either strong or weak, they are also weak solutions. Let them be ![]() and
and ![]() (remember that a weak solution is a pair of the ‘solution itself’ and a Wiener process). Then, since by the theorem there are strong solutions, let
(remember that a weak solution is a pair of the ‘solution itself’ and a Wiener process). Then, since by the theorem there are strong solutions, let ![]() and
and ![]() be the strong solutions corresponding to the Wiener process choices
be the strong solutions corresponding to the Wiener process choices ![]() and
and ![]() . By Picard's method of successive approximations given by 7.7– 7.8
, the approximating sequences have the same finite‐dimensional distributions, so the same happens to their a.s. limits
. By Picard's method of successive approximations given by 7.7– 7.8
, the approximating sequences have the same finite‐dimensional distributions, so the same happens to their a.s. limits ![]() and
and ![]() .
.
It is important to stress that, under the conditions assumed in the existence and uniqueness Theorem 7.1, from the probabilistic point of view, i.e. from the point of view of finite‐dimensional distributions, there is no difference between weak and strong solutions nor between the different possible weak solutions. This may be convenient since, to determine the probabilistic properties of the strong solution, we may work with weak solutions and get the same results.
Sometimes the Lipschitz condition or the restriction on growth are not valid and so the existence of strong solution is not guaranteed. In that case, one can see if there are weak solutions. Conditions for the existence of weak solutions can be seen in Stroock and Varadhan (2006) and Karatzas and Shreve (1991). Another interesting result is (see Karatzas and Shreve (1991)) that, if there is a weak solution and strong uniqueness holds, then there is a strong solution.
We have seen that, when ![]() and
and ![]() , besides satisfying the other assumptions of the existence and uniqueness Theorem 7.1, were also continuous functions of time, the solution of the SDE was a diffusion process with drift coefficient
, besides satisfying the other assumptions of the existence and uniqueness Theorem 7.1, were also continuous functions of time, the solution of the SDE was a diffusion process with drift coefficient ![]() and diffusion coefficient
and diffusion coefficient ![]() .
.
The reciprocal problem is also interesting. Given a diffusion process ![]() (
(![]() ) in a complete probability space
) in a complete probability space ![]() with drift coefficient
with drift coefficient ![]() and diffusion coefficient
and diffusion coefficient ![]() , is there an SDE which has such a process as a weak solution? Under appropriate regularity conditions, the answer is positive. Some results on this issue can be seen in Stroock and Varadhan (2006), Karatzas and Shreve (1991), and Gihman and Skorohod (1972). So, in a way, there is a correspondence between solutions of SDE and diffusion processes.
, is there an SDE which has such a process as a weak solution? Under appropriate regularity conditions, the answer is positive. Some results on this issue can be seen in Stroock and Varadhan (2006), Karatzas and Shreve (1991), and Gihman and Skorohod (1972). So, in a way, there is a correspondence between solutions of SDE and diffusion processes.
In the particular case that ![]() and
and ![]() do not depend on time (and satisfy the assumptions of the existence and uniqueness Theorem 7.1), they are automatically continuous functions of time and therefore the solution of the SDE will be a homogeneous diffusion process with drift coefficient
do not depend on time (and satisfy the assumptions of the existence and uniqueness Theorem 7.1), they are automatically continuous functions of time and therefore the solution of the SDE will be a homogeneous diffusion process with drift coefficient ![]() and diffusion coefficient
and diffusion coefficient ![]() . In this case, the SDE is an autonomous stochastic differential equation and its solution is also called an Itô diffusion. In this case, one does not need to verify the restriction on growth assumption since this is a direct consequence of the Lipschitz condition (this latter condition, of course, needs to be checked). In the autonomous case, one can work in the interval
. In this case, the SDE is an autonomous stochastic differential equation and its solution is also called an Itô diffusion. In this case, one does not need to verify the restriction on growth assumption since this is a direct consequence of the Lipschitz condition (this latter condition, of course, needs to be checked). In the autonomous case, one can work in the interval ![]() since
since ![]() and
and ![]() do not depend on time.
do not depend on time.
In the autonomous case, under the assumptions of the existence and uniqueness Theorem 7.1, one can even conclude that the solution of the SDE is a strong Markov process (see, for instance, Gihman and Skorohod (1972) or Øksendal (2003)).
In the autonomous case, if we are working in one dimension (so this is not generalizable to multidimensional SDEs), we can get results even when the Lipschitz condition fails but ![]() and
and ![]() are continuously differentiable (i.e. are of class
are continuously differentiable (i.e. are of class ![]() ). Note that, if they are of class
). Note that, if they are of class ![]() , they may or may not verify a Lipschitz condition; if they have bounded derivatives, they satisfy a Lipschitz condition, but this is not the case if the derivatives are unbounded.
, they may or may not verify a Lipschitz condition; if they have bounded derivatives, they satisfy a Lipschitz condition, but this is not the case if the derivatives are unbounded.
The result by McKean (1969) for autonomous one‐dimensional SDEs is that, if ![]() and
and ![]() are of class
are of class ![]() , then there is a unique (strong) solution up to a possible explosion time
, then there is a unique (strong) solution up to a possible explosion time ![]() . By explosion, we mean the solution becoming
. By explosion, we mean the solution becoming ![]() . If
. If ![]() and
and ![]() also satisfy a Lipschitz condition, that is sufficient to prevent explosions (i.e. one has
also satisfy a Lipschitz condition, that is sufficient to prevent explosions (i.e. one has ![]() a.s.) and the solution exists for all times and is unique. If
a.s.) and the solution exists for all times and is unique. If ![]() and
and ![]() are of class
are of class ![]() but fail to satisfy a Lipschitz condition, one cannot exclude the possibility of an explosion, but there are cases in which one can show that an explosion is not possible (or, more precisely, has a zero probability of occurring) and therefore the solution exists for all times and is unique. We will see later some examples of such cases and of the simple methods used to show that in such cases there is no explosion. There is also a test to determine whether an explosion will or will not occur, the Feller test (see McKean (1969)).
but fail to satisfy a Lipschitz condition, one cannot exclude the possibility of an explosion, but there are cases in which one can show that an explosion is not possible (or, more precisely, has a zero probability of occurring) and therefore the solution exists for all times and is unique. We will see later some examples of such cases and of the simple methods used to show that in such cases there is no explosion. There is also a test to determine whether an explosion will or will not occur, the Feller test (see McKean (1969)).
Let us now consider multidimensional stochastic differential equations. The setting is similar to that of the multidimensional Itô processes of Section 6.7. The difference is that now one uses ![]() and
and ![]() . The Lipschitz condition and the restriction on growth of
. The Lipschitz condition and the restriction on growth of ![]() and
and ![]() in the existence and uniqueness Theorem 7.1 are identical with
in the existence and uniqueness Theorem 7.1 are identical with ![]() representing the euclidean distance. The results of Theorem 7.1 remain valid. When the solution is a diffusion process, the drift coefficient is the vector
representing the euclidean distance. The results of Theorem 7.1 remain valid. When the solution is a diffusion process, the drift coefficient is the vector ![]() and the diffusion coefficient is the matrix
and the diffusion coefficient is the matrix ![]() .
.
Notice, however, that, given a multidimensional diffusion process with drift coefficient ![]() and diffusion coefficient
and diffusion coefficient ![]() , there are several matrices
, there are several matrices ![]() for which
for which ![]() , but all of them result in the same probabilistic properties for the solution of the SDE. So, from the point of view of probabilistic properties or of weak solutions, it is irrelevant which
, but all of them result in the same probabilistic properties for the solution of the SDE. So, from the point of view of probabilistic properties or of weak solutions, it is irrelevant which ![]() one chooses.
one chooses.
The treatment in this chapter allows the inclusion of SDE of the type
by adding the equation ![]() and working in two dimensions with the vector
and working in two dimensions with the vector ![]() and the SDE
and the SDE
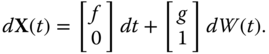
The initial condition takes the form ![]() . Note that
. Note that ![]() and
and ![]() .
.
We can also have higher order stochastic differential equations of the form (here the superscript ![]() represents the derivative of order
represents the derivative of order ![]() )
)
with initial conditions ![]() (
(![]() ). For that, we use the same technique that is used for higher order ODEs, working with the vector
). For that, we use the same technique that is used for higher order ODEs, working with the vector
and the SDE
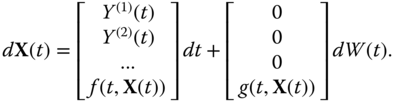
We can also have functions ![]() and
and ![]() that depend on chance
that depend on chance ![]() in a more general direct way (thus far they did not depend directly on chance, but they did so indirectly through
in a more general direct way (thus far they did not depend directly on chance, but they did so indirectly through ![]() ). This poses no problem as long as
). This poses no problem as long as ![]() and
and ![]() are kept non‐anticipative.
are kept non‐anticipative.
