Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

6.3 The Adjoint of a Linear Operator

In Section 6.1, we defined the conjugate transpose A* of a matrix A. For a linear operator T on an inner product space v, we now define a related linear operator on V called the adjoint of T, whose matrix representation with respect to any orthonormal basis β $β$ for V is [T]*β ${[T]}_{β}^{*}$ . The analogy between conjugation of complex numbers and adjoints of linear operators will become apparent. We first need a preliminary result.

Let V be an inner product space, and let y∈V $y \in V$ . The function g:V→F $g : V \to F$ defined by g(x)=⟨x, y⟩ $g (x) = 〈 x, y 〉$ is clearly linear. More interesting is the fact that if V is finite-dimensional, every linear transformation from V into F is of this form.

Theorem 6.8.

Let V be a finite-dimensional inner product space over F, and let g: V→F $g : V \to F$ be a linear transformation. Then there exists a unique vector y∈V $y \in V$ such that g(x)=⟨x, y⟩ $g (x) = 〈 x, y 〉$ for all x∈V $x \in V$ .

Proof.

Let β={v1, v2, …, vn} $β = {v_{1}, v_{2}, \dots, v_{n}}$ be an orthonormal basis for V, and let

y = \sum i = 1 n g (v i) ¯ ¯ ¯ ¯ ¯ ¯ ¯ v i .

$y = \sum_{i = 1}^{n} \bar{g (v_{i})} v_{i} .$

Define h: V→F $h : V \to F$ , by h(x)=⟨x, y⟩ $h (x) = 〈 x, y 〉$ , which is clearly linear. Furthermore, for 1≤j≤n $1 \leq j \leq n$ we have

h (v j) = ⟨ v j, y ⟩ = ⟨ v j, \sum i = 1 n g (v i) ¯ ¯ ¯ ¯ ¯ ¯ ¯ v i ⟩ = \sum i = 1 n g (v i) (v j, v i) = \sum i = 1 n g (v i) δ j i = g (v j) .

$\begin{array}{l} h (v_{j}) = 〈 v_{j}, y 〉 = ⟨ v_{j}, \sum_{i = 1}^{n} \bar{g (v_{i})} v_{i} ⟩ \\ = \sum_{i = 1}^{n} g (v_{i}) (v_{j}, v_{i}) = \sum_{i = 1}^{n} g (v_{i}) δ_{j i} = g (v_{j}) . \end{array}$

Since g and h agree on β $β$ , we have that g=h $g = h$ by the corollary to Theorem 2.6 (p. 73).

To show that y is unique, suppose that g(x)=⟨x, y′⟩ $g (x) = 〈 x, y^{'} 〉$ for all x. Then ⟨x, y⟩=⟨x, y′⟩ $〈 x, y 〉 = 〈 x, y^{'} 〉$ for all x; so by Theorem 6.1(e) (p. 331), we have y=y′ $y = y^{'}$ .

Example 1

Define g: R2→R $g : R^{2} \to R$ by g(a1, a2)=2a1+a2; $g (a_{1}, a_{2}) = 2 a_{1} + a_{2};$ clearly g is a linear transformation. Let β={e1, e2} $β = {e_{1}, e_{2}}$ , and let y=g(e1)e1+g(e2)e2=2e1+e2=(2, 1) $y = g (e_{1}) e_{1} + g (e_{2}) e_{2} = 2 e_{1} + e_{2} = (2, 1)$ , as in the proof of Theorem 6.8. Then g(a1, a2)=⟨(a1, a2), (2, 1)⟩=2a1+a2 $g (a_{1}, a_{2}) = 〈 (a_{1}, a_{2}), (2, 1) 〉 = 2 a_{1} + a_{2}$ .

Theorem 6.9.

Let V be a finite-dimensional inner product space, and let T be a linear operator on V. Then there exists a unique function T*: V→V $T * : V \to V$ such that ⟨T(x), y⟩=⟨x, T*(y)⟩ $〈 T (x), y 〉 = 〈 x, T * (y) 〉$ for all x, y∈V $x, y \in V$ . Furthermore, T* is linear.

Proof.

Let y∈V $y \in V$ . Define g: V→F $g : V \to F$ by g(x)=⟨T(x), y⟩ $g (x) = 〈 T (x), y 〉$ for all x∈V $x \in V$ . We first show that g is linear. Let x1, x2∈V $x_{1}, x_{2} \in V$ and c∈F $c \in F$ . Then

g (c x 1 + x 2) = = ⟨ T (c x 1 + x 2), y ⟩ = ⟨ c T (x 1) + T (x 2), y ⟩ c ⟨ T (x 1), y ⟩ + ⟨ T (x 2), y ⟩ = c g (x 1) + g (x 2) .

$\begin{array}{rcl} g (c x_{1} + x_{2}) & = & 〈 T (c x_{1} + x_{2}), y 〉 = 〈 c T (x_{1}) + T (x_{2}), y 〉 \\ = & c 〈 T (x_{1}), y 〉 + 〈 T (x_{2}), y 〉 = c g (x_{1}) + g (x_{2}) . \end{array}$

Hence g is linear.

We now apply Theorem 6.8 to obtain a unique vector y′∈V $y^{'} \in V$ such that g(x)=⟨x, y′⟩ $g (x) = 〈 x, y^{'} 〉$ ; that is, ⟨T(x), y⟩=⟨x, y′⟩ $〈 T (x), y 〉 = 〈 x, y^{'} 〉$ for all x∈V $x \in V$ . Defining T*: V→V $T * : V \to V$ by T*(y)=y′ $T * (y) = y^{'}$ , we have ⟨T(x), y⟩=⟨x, T*(y)⟩ $〈 T (x), y 〉 = 〈 x, T * (y) 〉$ .

To show that T* is linear, let y1, y2∈V $y_{1}, y_{2} \in V$ and c∈F $c \in F$ . Then for any x∈V $x \in V$ , we have

⟨ x, T * (c y 1 + y 2) ⟩ = = = = ⟨ T (x), c y 1 + y 2 ⟩ c ¯ ⟨ T (x), y 1 ⟩ + ⟨ T (x), y 2 ⟩ c ¯ ⟨ x, T * (y 1) ⟩ + ⟨ x, T * (y 2) ⟩ ⟨ x, c T * (y 1) + T * (y 2) ⟩ .

$\begin{array}{rcl} 〈 x, T * (c y_{1} + y_{2}) 〉 & = & 〈 T (x), c y_{1} + y_{2} 〉 \\ = & \bar{c} 〈 T (x), y_{1} 〉 + 〈 T (x), y_{2} 〉 \\ = & \bar{c} 〈 x, T * (y_{1}) 〉 + 〈 x, T * (y_{2}) 〉 \\ = & 〈 x, c T * (y_{1}) + T * (y_{2}) 〉 . \end{array}$

Since x is arbitrary, T*(cy1+y2)=cT*(y1)+T*(y2) $T * (c y_{1} + y_{2}) = c T * (y_{1}) + T * (y_{2})$ by Theorem 6.1(e) (p. 331).

Finally, we need to show that T* is unique. Suppose that U: V→V $U : V \to V$ is linear and that it satisfies ⟨T(x), y⟩=⟨x, U(y)⟩ $〈 T (x), y 〉 = 〈 x, U (y) 〉$ for all x, y∈V $x, y \in V$ . Then ⟨x, T*(y)⟩=⟨x, U(y)⟩ $〈 x, T * (y) 〉 = 〈 x, U (y) 〉$ for all x, y∈V $x, y \in V$ , so T*=U $T * = U$ .

The linear operator T* described in Theorem 6.9 is called the adjoint of the operator T. The symbol T^* is read “T star.”

Thus T* is the unique operator on V satisfying ⟨T(x), y⟩=⟨x, T*(y)⟩ $〈 T (x), y 〉 = 〈 x, T * (y) 〉$ for all x, y∈V $x, y \in V$ . Note that we also have

⟨ x, T (y) ⟩ = ⟨ T (y), x ⟩ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ = ⟨ y, T * (x) ⟩ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ = ⟨ T * (x), y ⟩;

$〈 x, T (y) 〉 = \bar{〈 T (y), x 〉} = \bar{〈 y, T * (x) 〉} = 〈 T * (x), y 〉;$

so ⟨x, T(y)⟩=⟨T*(x), y⟩ $〈 x, T (y) 〉 = 〈 T * (x), y 〉$ for all x, y∈V $x, y \in V$ . We may view these equations symbolically as adding a * to T when shifting its position inside the inner product symbol.

For an infinite-dimensional inner product space, the adjoint of a linear operator T may be defined to be the function T* such that ⟨T(x), y⟩=⟨x, T*(y)⟩ $〈 T (x), y 〉 = 〈 x, T * (y) 〉$ for all x, y∈V $x, y \in V$ , provided it exists. Although the uniqueness and linearity of T^* follow as before, the existence of the adjoint is not guaranteed (see Exercise 24). The reader should observe the necessity of the hypothesis of finite-dimensionality in the proof of Theorem 6.8. Many of the theorems we prove about adjoints, nevertheless, do not depend on V being finite-dimensional.

Theorem 6.10 is a useful result for computing adjoints.

Theorem 6.10.

Let V be a finite-dimensional inner product space, and let β $β$ be an orthonormal basis for V. If T is a linear operator on V, then

[T *] β = [T] * β .

${[T *]}_{β} = {[T]}_{β}^{*} .$

Proof.

Let A=[T]β, B=[T*]β, $A = {[T]}_{β}, B = {[T *]}_{β},$ and β={v1, v2, …, vn} $β = {v_{1}, v_{2}, \dots, v_{n}}$ . Then from the corollary to Theorem 6.5 (p. 344), we have

B i j = ⟨ T * (v j), v i ⟩ = ⟨ v i, T * (v j) ⟩ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ = ⟨ T (v i), v j ⟩ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ = A ¯ ¯ ¯ j i = (A *) i j .

$B_{i j} = 〈 T * (v_{j}), v_{i} 〉 = \bar{〈 v_{i}, T * (v_{j}) 〉} = \bar{〈 T (v_{i}), v_{j} 〉} = {\bar{A}}_{j i} = {(A *)}_{i j} .$

Hence B=A* $B = A *$ .

Corollary.

Let A be an n×n $n \times n$ matrix. Then LA*=(LA)* $L_{A *} = (L_{A}) *$ .

Proof.

If β $β$ is the standard ordered basis for Fn $F^{n}$ , then, by Theorem 2.16 (p. 94), we have [LA]β=A ${[L_{A}]}_{β} = A$ . Hence [(LA)*]β=[LA]*β=A*=[LA*]β ${[(L_{A}) *]}_{β} = {[L_{A}]}_{β}^{*} = A * = {[L_{A *}]}_{β}$ , and so (LA)*=LA* $(L_{A}) * = L_{A *}$ .

As an illustration of Theorem 6.10, we compute the adjoint of a specific linear operator.

Example 2

Let T be the linear operator on C2 $C^{2}$ defined by T(a1, a2)=(2ia1+3a2, a1−a2) $T (a_{1}, a_{2}) = (2 i a_{1} + 3 a_{2}, a_{1} - a_{2})$ . If β $β$ is the standard ordered basis for C2 $C^{2}$ , then

[T] β = (2 i 1 3 - 1) .

${[T]}_{β} = (\begin{array}{r} 2 i & 3 \\ 1 & - 1 \end{array}) .$

[T *] β = [T] * β = (- 2 i 3 1 - 1) .

${[T *]}_{β} = {[T]}_{β}^{*} = (\begin{array}{r} - 2 i & 1 \\ 3 & - 1 \end{array}) .$

Hence

T * (a 1, a 2) = (- 2 i a 1 + a 2, 3 a 1 - a 2) .

$T * (a_{1}, a_{2}) = (- 2 i a_{1} + a_{2}, 3 a_{1} - a_{2}) .$

The following theorem suggests an analogy between the conjugates of complex numbers and the adjoints of linear operators.

Theorem 6.11.

Let V be an inner product space, and let T and U be linear operators on V whose adjoints exist. Then

(a) T+U $T + U$ has an adjoint, and (T+U)*=T*+U* $(T + U) * = T * + U *$ .
(b) cT has an adjoint, and (cT)*=c¯T* $(c T) * = \bar{c} T *$ for any c∈F $c \in F$ .
(c) TU has an adjoint, and (TU)*=U*T* $(TU) * = U * T *$ .
(d) T* has an adjoint, and T**=T $T * * = T$ .
(e) I has an adjoint, and I*=I $I * = I$ .

Proof.

We prove (a) and (d); the rest are proved similarly. Let x, y∈V $x, y \in V$ .

(a) Because

⟨ (T + U) (x), y ⟩ = = = ⟨ T (x) + U (x), y ⟩ ⟨ x, T * (y) ⟩ + ⟨ x, U * (y) ⟩ ⟨ x, T * (y) + U * (y) ⟩ = ⟨ x, (T * + U *) (y) ⟩,

$\begin{array}{rcl} 〈 (T + U) (x), y 〉 & = & 〈 T (x) + U (x), y 〉 \\ = & 〈 x, T * (y) 〉 + 〈 x, U * (y) 〉 \\ = & 〈 x, T * (y) + U * (y) 〉 = 〈 x, (T * + U *) (y) 〉, \end{array}$

it follows that (T+U)* $(T + U) *$ exists and is equal to T*+U* $T * + U *$ .

(d) Similarly, since

⟨ T * (x), y ⟩, = ⟨ x, T (y) ⟩,

$〈 T * (x), y 〉, = 〈 x, T (y) 〉,$

(d) follows.

Unless stated otherwise, for the remainder of this chapter we adopt the convention that a reference to the adjoint of a linear operator on an infinite-dimensional inner product space assumes its existence.

Corollary.

Let A and B be n×n $n \times n$ matrices. Then

(a) (A+B)*=A*+B*. $(A + B) * = A * + B * .$
(b) (cA)*=c¯A* $(c A) * = \bar{c} A *$ for all c∈F. $c \in F .$
(c) (AB)*=B*A*. $(A B) * = B * A * .$
(d) A**=A. $A * * = A .$
(e) I*=I $I * = I$

Proof.

We prove only (c); the remaining parts can be proved similarly.

Since L(AB)*=(LAB)*=(LALB)*=(LB)*(LA)*=LB*LA*=LB*A* $L_{(A B) *} = (L_{A B}) * = (L_{A} L_{B}) * = (L_{B}) * (L_{A}) * = L_{B *} L_{A *} = L_{B * A *}$ , we have (AB)*=B*A* $(A B) * = B * A *$ .

In the preceding proof, we relied on the corollary to Theorem 6.10. An alternative proof, which holds even for nonsquare matrices, can be given by appealing directly to the definition of the conjugate transpose of a matrix (see Exercise 5).

Least Squares Approximation

Consider the following problem: An experimenter collects data by taking measurements y1, y2, …, ym $y_{1}, y_{2}, \dots, y_{m}$ at times t1, t2, …, tm $t_{1}, t_{2}, \dots, t_{m}$ , respectively. For example, he or she may be measuring unemployment at various times during some period. Suppose that the data (t1, y1), (t2, y2), …, (tm, ym) $(t_{1}, y_{1}), (t_{2}, y_{2}), \dots, (t_{m}, y_{m})$ are plotted as points in the plane. (See Figure 6.3.) From this plot, the experimenter feels that there exists an essentially linear relationship between y and t, say y=ct+d $y = c t + d$ , and would like to find the constants c and d so that the line y=ct+d $y = c t + d$ represents the best possible fit to the data collected. One such estimate of fit is to calculate the error E that represents the sum of the squares of the vertical distances from the points to the line; that is,

E = \sum i = 1 m (y i - c t i - d) 2 .

$E = \sum_{i = 1}^{m} {(y_{i} - c t_{i} - d)}^{2} .$

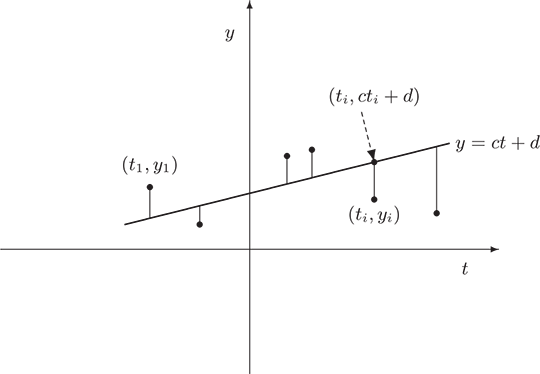
A graph to measure unemployment at various times during a particular period. — Figure 6.3

Figure 6.3 Full Alternative Text

Thus the problem is reduced to finding the constants c and d that minimize E. (For this reason the line y=ct+d $y = c t + d$ is called the least squares line.) If we let

A = ⎛ ⎝ ⎜ ⎜ ⎜ ⎜ t 1 t 2 ⋮ t m 11 ⋮ 1 ⎞ ⎠ ⎟ ⎟ ⎟ ⎟, x = (c d), and y = ⎛ ⎝ ⎜ ⎜ ⎜ ⎜ y 1 y 2 ⋮ y m ⎞ ⎠ ⎟ ⎟ ⎟ ⎟,

$A = (\begin{array}{c} t_{1} & 1 \\ t_{2} & 1 \\ ⋮ & ⋮ \\ t_{m} & 1 \end{array}), x = (\begin{array}{c} c \\ d \end{array}), and y = (\begin{array}{c} y_{1} \\ y_{2} \\ ⋮ \\ y_{m} \end{array}),$

then it follows that E=||y−Ax||2 $E = | | y - A x | |^{2}$ .

We develop a general method for finding an explicit vector x0∈Fn $x_{0} \in F^{n}$ that minimizes E; that is, given an m×n $m \times n$ matrix A, we find x0∈Fn $x_{0} \in F^{n}$ such that ||y−Ax0||≤||y−Ax|| $| | y - A x_{0} | | \leq | | y - A x | |$ for all vectors x∈Fn $x \in F^{n}$ . This method not only allows us to find the linear function that best fits the data, but also, for any positive integer k, the best fit using a polynomial of degree at most k.

First, we need some notation and two simple lemmas. For x, y∈Fn $x, y \in F^{n}$ , let ⟨x, y⟩n ${〈 x, y 〉}_{n}$ denote the standard inner product of x and y in Fn $F^{n}$ . Recall that if x and y are regarded as column vectors, then ⟨x, y⟩n=y*x ${〈 x, y 〉}_{n} = y * x$ .

Lemma 1.

Let A∈Mm×n(F), x∈Fn $A \in M_{m \times n} (F), x \in F^{n}$ , and y∈Fm $y \in F^{m}$ . Then

⟨ A x, y ⟩ m = ⟨ x, A * y ⟩ n .

${〈 A x, y 〉}_{m} = {〈 x, A * y 〉}_{n} .$

Proof.

By a generalization of the corollary to Theorem 6.11 (see Exercise 5(b)), we have

⟨ A x, y ⟩ m = y * (A x) = (y * A) x = (A * y) * x = ⟨ x, A * y ⟩ n .

${〈 A x, y 〉}_{m} = y * (A x) = (y * A) x = (A * y) * x = {〈 x, A * y 〉}_{n} .$

Lemma 2.

Let A∈Mm×n(F) $A \in M_{m \times n} (F)$ . Then rank(A*A)=rank(A) $rank (A * A) = rank (A)$ .

Proof.

By the dimension theorem, we need only show that, for x∈Fn $x \in F^{n}$ , we have A*Ax=0 $A * A x = 0$ if and only if Ax=0 $A x = 0$ . Clearly, Ax=0 $A x = 0$ implies that A*Ax=0 $A * A x = 0$ . So assume that A*Ax=0 $A * A x = 0$ . Then

0 = ⟨ A * A x, x ⟩ n = ⟨ A x, A * * x ⟩ m = ⟨ A x, A x ⟩ m,

$0 = {〈 A * A x, x 〉}_{n} = {〈 A x, A * * x 〉}_{m} = {〈 A x, A x 〉}_{m},$

so that Ax=0 $A x = 0$ .

Corollary.

If A is an m×n $m \times n$ matrix such that rank(A)=n $rank (A) = n$ , then A*A $A * A$ is invertible.

Now let A be an m×n $m \times n$ matrix and y∈Fm $y \in F^{m}$ . Define W={Ax: x∈Fn}; $W = {A x : x \in F^{n}};$ that is, W=R(LA) $W = R (L_{A})$ . By the corollary to Theorem 6.6 (p. 347), there exists a unique vector in W that is closest to y. Call this vector Ax0 $A x_{0}$ , where x0∈Fn $x_{0} \in F^{n}$ . Then ||Ax0−y||≤||Ax−y|| $| | A x_{0} - y | | \leq | | A x - y | |$ for all x∈Fn $x \in F^{n}$ ; so x0 $x_{0}$ has the property that E=||Ax0−y|| $E = | | A x_{0} - y | |$ is minimal, as desired.

To develop a practical method for finding such an x₀, we note from Theorem 6.6 and its corollary that Ax0−y∈W⊥; $A x_{0} - y \in W^{⊥};$ so ⟨Ax, Ax0−y⟩m=0 ${〈 A x, A x_{0} - y 〉}_{m} = 0$ for all x∈Fn $x \in F^{n}$ . Thus, by Lemma 1, we have that ⟨x, A*(Ax0−y)⟩n=0 ${〈 x, A * (A x_{0} - y) 〉}_{n} = 0$ for all x∈Fn $x \in F^{n}$ ; that is, A*(Ax0−y)=0 $A * (A x_{0} - y) = 0$ . So we need only find a solution x0 $x_{0}$ to A*Ax=A*y $A * A x = A * y$ . If, in addition, we assume that rank(A)=n $rank (A) = n$ , then by Lemma 2 we have x0=(A*A)−1A*y $x_{0} = {(A * A)}^{- 1} A * y$ . We summarize this discussion in the following theorem.

Theorem 6.12.

Let A∈Mm×n(F) $A \in M_{m \times n} (F)$ and y∈Fm $y \in F^{m}$ . Then there exists x0∈Fn $x_{0} \in F^{n}$ such that (A*A)x0=A*y $(A * A) x_{0} = A * y$ and ||Ax0−y||≤||Ax−y|| $| | A x_{0} - y | | \leq | | A x - y | |$ for all x∈Fn $x \in F^{n}$ . Furthermore, if rank(A)=n $rank (A) = n$ , then x0=(A*A)−1A*y $x_{0} = {(A * A)}^{- 1} A * y$ .

To return to our experimenter, let us suppose that the data collected are (1, 2), (2, 3), (3, 5), and (4, 7). Then

A = ⎛ ⎝ ⎜ ⎜ ⎜ 12341111 ⎞ ⎠ ⎟ ⎟ ⎟ and y = ⎛ ⎝ ⎜ ⎜ ⎜ 2357 ⎞ ⎠ ⎟ ⎟ ⎟;

$A = (\begin{array}{c} 1 & 1 \\ 2 & 1 \\ 3 & 1 \\ 4 & 1 \end{array}) and y = (\begin{array}{c} 2 \\ 3 \\ 5 \\ 7 \end{array});$

hence

A * A = (11213141) ⎛ ⎝ ⎜ ⎜ ⎜ 12341111 ⎞ ⎠ ⎟ ⎟ ⎟ = (3010104) .

$A * A = (\begin{array}{r} 1 & 2 & 3 & 4 \\ 1 & 1 & 1 & 1 \end{array}) (\begin{array}{r} 1 & 1 \\ 2 & 1 \\ 3 & 1 \\ 4 & 1 \end{array}) = (\begin{array}{r} 30 & 10 \\ 10 & 4 \end{array}) .$

Thus

(A * A) - 1 = 1 20 (4 - 10 - 10 30) .

${(A * A)}^{- 1} = \frac{1}{20} (\begin{array}{r} 4 & - 10 \\ - 10 & 30 \end{array}) .$

Therefore

(c d) = x 0 = 1 20 (4 - 10 - 10 30) (11213141) ⎛ ⎝ ⎜ ⎜ ⎜ 2357 ⎞ ⎠ ⎟ ⎟ ⎟ = (1.7 0) .

$(\begin{array}{r} c \\ d \end{array}) = x_{0} = \frac{1}{20} (\begin{array}{r} 4 & - 10 \\ - 10 & 30 \end{array}) (\begin{array}{r} 1 & 2 & 3 & 4 \\ 1 & 1 & 1 & 1 \end{array}) (\begin{array}{r} 2 \\ 3 \\ 5 \\ 7 \end{array}) = (\begin{array}{r} 1.7 \\ 0 \end{array}) .$

It follows that the line y=1.7t $y = 1.7 t$ is the least squares line. The error E may be computed directly as ||Ax0−y||2=0.3 $| | A x_{0} - y | |^{2} = 0.3$ .

Suppose that the experimenter chose the times ti(1≤i≤m) $t_{i} (1 \leq i \leq m)$ to satisfy

\sum i = 1 m t i = 0.

$\sum_{i = 1}^{m} t_{i} = 0.$

Then the two columns of A would be orthogonal, so A * A would be a diagonal matrix (see Exercise 19). In this case, the computations are greatly simplified.

In practice, the m×2 $m \times 2$ matrix A in our least squares application has rank equal to two, and hence A * A is invertible by the corollary to Lemma 2. For, otherwise, the first column of A is a multiple of the second column, which consists only of ones. But this would occur only if the experimenter collects all the data at exactly one time.

Finally, the method above may also be applied if, for some k, the experimenter wants to fit a polynomial of degree at most k to the data. For instance, if a polynomial y=ct2+dt+e $y = c t^{2} + d t + e$ of degree at most 2 is desired, the appropriate model is

x = ⎛ ⎝ ⎜ c d e ⎞ ⎠ ⎟, y = ⎛ ⎝ ⎜ ⎜ ⎜ ⎜ y 1 y 2 ⋮ y m ⎞ ⎠ ⎟ ⎟ ⎟ ⎟, and A = ⎛ ⎝ ⎜ ⎜ t 21 ⋮ t 2 m t 1 ⋮ t m 1 ⋮ 1 ⎞ ⎠ ⎟ ⎟ .

$x = (\begin{array}{c} c \\ d \\ e \end{array}), y = (\begin{array}{c} y_{1} \\ y_{2} \\ ⋮ \\ y_{m} \end{array}), and A = (\begin{array}{c} t_{1}^{2} & t_{1} & 1 \\ ⋮ & ⋮ & ⋮ \\ t_{m}^{2} & t_{m} & 1 \end{array}) .$

Minimal Solutions to Systems of Linear Equations

Even when a system of linear equations Ax=b $A x = b$ is consistent, there may be no unique solution. In such cases, it may be desirable to find a solution of minimal norm. A solution s to Ax=b $A x = b$ is called a minimal solution if ||s||≤||u|| $| | s | | \leq | | u | |$ for all other solutions u. The next theorem assures that every consistent system of linear equations has a unique minimal solution and provides a method for computing it.

Theorem 6.13.

Let A∈Mm×n(F) $A \in M_{m \times n} (F)$ and b∈Fm $b \in F^{m}$ . Suppose that Ax=b $A x = b$ is consistent. Then the following statements are true.

There exists exactly one minimal solution s of Ax=b $A x = b$ , and s∈R(LA*) $s \in R (L_{A *})$ .
The vector s is the only solution to Ax=b $A x = b$ that lies in R(LA*) $R (L_{A *})$ ; in fact, if u satisfies (AA*)u=b $(A A *) u = b$ , then s=A*u $s = A * u$ .

Proof.

(a) For simplicity of notation, we let W=R(LA*) $W = R (L_{A *})$ and W′=N(LA) $W^{'} = N (L_{A})$ . Let x be any solution to Ax=b $A x = b$ . By Theorem 6.6 (p. 347), x=s+y $x = s + y$ for some s∈W $s \in W$ and y∈W⊥ $y \in W^{⊥}$ . But W⊥=W′ $W^{⊥} = W^{'}$ by Exercise 12, and therefore b=Ax=As+Ay=As $b = A x = A s + A y = A s$ . So s is a solution to Ax=b $A x = b$ that lies in W. To prove (a), we need only show that s is the unique minimal solution. Let v be any solution to Ax=b $A x = b$ . By Theorem 3.9 (p. 172), we have that v=s+u $v = s + u$ , where u∈W′ $u \in W^{'}$ . Since s∈W $s \in W$ , which equals W′⊥ ${W^{'}}^{⊥}$ by Exercise 12, we have

| | v | | 2 = | | s + u | | 2 = | | s | | 2 + | | u | | 2 \geq | | s | | 2

$| | v | |^{2} = | | s + u | |^{2} = | | s | |^{2} + | | u | |^{2} \geq | | s | |^{2}$

by Exercise 10 of Section 6.1. Thus s is a minimal solution. We can also see from the preceding calculation that if ||v||=||s|| $| | v | | = | | s | |$ , then u=0 $u = 0$ ; hence v=s $v = s$ . Therefore s is the unique minimal solution to Ax=b $A x = b$ , proving (a).

(b) Assume that v is also a solution to Ax=b $A x = b$ that lies in W. Then

v - s \in W \cap W' = W \cap W ⊥ = {0};

$v - s \in {W \cap W}^{'} = W \cap W^{⊥} = {0};$

so v=s $v = s$ .

Finally, suppose that (AA*)u=b $(A A *) u = b$ , and let v=A*u $v = A * u$ . Then v∈W $v \in W$ and Av=b $A v = b$ . Therefore s=v=A*u $s = v = A * u$ by the discussion above.

Example 3

Consider the system

x x x + - + 2 y y 5 y + + z 2 z = = = 4 - 11 19.

$\begin{array}{rrrrrcr} x & + & 2 y & + & z & = & 4 \\ x & - & y & + & 2 z & = & - 11 \\ x & + & 5 y & = & 19. \end{array}$

Let

$A = (\begin{array}{r} 1 & 2 & 1 \\ 1 & - 1 & 2 \\ 1 & 5 & 0 \end{array}) and b = (\begin{array}{r} 4 \\ - 11 \\ 19 \end{array}) .$

To find the minimal solution to this system, we must first find some solution u to $A A * x = b$ . Now

$A A * = (\begin{array}{r} 6 & 1 & 11 \\ 1 & 6 & - 4 \\ 11 & - 4 & 26 \end{array});$

so we consider the system

$\begin{array}{rrrrrcr} 6 x & + & y & + & 11 z & = & 4 \\ x & + & 6 y & - & 4 z & = & - 11 \\ 11 x & - & 4 y & + & 26 z & = & 19, \end{array}$

for which one solution is

$u = (\begin{array}{r} 1 \\ - 2 \\ 0 \end{array}) .$

(Any solution will suffice.) Hence

$s = A * u = (\begin{array}{r} - 1 \\ 4 \\ - 3 \end{array})$

is the minimal solution to the given system.

Exercises

Label the following statements as true or false. Assume that the underlying inner product spaces are finite-dimensional.
1. (a) Every linear operator has an adjoint.
2. (b) Every linear operator on V has the form $x \to 〈 x, y 〉$ for some $y \in V$ .
3. (c) For every linear operator T on V and every ordered basis $β$ for V, we have ${[T *]}_{β} = ({[T]}_{β}) *$ .
4. (d) The adjoint of a linear operator is unique.
5. (e) For any linear operators T and U and scalars a and b,
  
  $(a T + b U) * = a T * + b U * .$
6. (f) For any $n \times n$ matrix A, we have $(L_{A}) * = L_{A *}$ .
7. (g) For any linear operator T, we have $(T *) * = T$ .
For each of the following inner product spaces V (over F) and linear transformations $g : V \to F$ , find a vector y such that $g (x) = 〈 x, y 〉$ for all $x \in V$ .
1. (a) $V = R^{3}, g (a_{1}, a_{2}, a_{3}) = a_{1} - 2 a_{2} + 4 a_{3}$
2. (b) $V = C^{2}, g (z_{1}, z_{2},) = z_{1} - 2 z_{2}$
3. (c) $V = P_{2} (R)$ with $〈 f (x), h (x) 〉 = \int_{0}^{1} f (t) h (t) d t, g (f) = f (0) + f^{'} (1)$
For each of the following inner product spaces V and linear operators T on V, evaluate T* at the given vector in V.
1. (a) $V = R^{2}, T (a, b) = (2 a + b, a - 3 b), x = (3, 5) .$
2. (b) $V = C^{2}, T (z_{1}, z_{2}) = (2 z_{1} + i z_{2}, (1 - i) z_{1}), x = (3 - i, 1 + 2 i) .$
3. (c) $V = P_{1} (R)$ with $〈 f (x), g (x) 〉 = \int_{- 1}^{1} f (t) g (t) d t, T (f) = f^{'} + 3 f, f (t) = 4 - 2 t$
Complete the proof of Theorem 6.11.
1. (a) Complete the proof of the corollary to Theorem 6.11 by using Theorem 6.11, as in the proof of (c).
2. (b) State a result for nonsquare matrices that is analogous to the corollary to Theorem 6.11, and prove it using a matrix argument.
Let T be a linear operator on an inner product space V. Let $U_{1} = T + T *$ and $U_{2} = TT *$ . Prove that $U_{1} = U_{1}^{*}$ and $U_{2} = U_{2}^{*}$ .
Give an example of a linear operator T on an inner product space V such that $N (T) \neq N (T *)$ .
Let V be a finite-dimensional inner product space, and let T be a linear operator on V. Prove that if T is invertible, then T* is invertible and ${(T *)}^{- 1} = (T^{- 1}) *$ .
Prove that if $V = W \oplus W^{⊥}$ and T is the projection on W along $W^{⊥}$ , then $T = T *$ . Hint: Recall that $N (T) = W^{⊥}$ . (For definitions, see the exercises of Sections 1.3 and (a) 2.1.)
Let T be a linear operator on an inner product space V. Prove that $| | T (x) | | = | | x | |$ for all $x \in V$ if and only if $〈 T (x), T (y) 〉 = 〈 x, y 〉$ for all $x, y \in V$ . Hint: Use Exercise 20 of Section 6.1.
For a linear operator T on an inner product space V, prove that $T * T = T_{0}$ implies $T = T_{0}$ . Is the same result true if we assume that $TT * = T_{0}$ ?
Let V be an inner product space, and let T be a linear operator on V. Prove the following results.
1. (a) $R {(T *)}^{⊥} = N (T) .$
2. (b) If V is finite-dimensional, then $R (T *) = N {(T)}^{⊥}$ ?. Hint: Use Exercise 13(c) of Section 6.2.
Let T be a linear operator on a finite-dimensional inner product space V. Prove the following results.
1. (a) $N (T * T) = N (T)$ . Deduce that $rank (T * T) = rank (T)$ .
2. (b) $rank (T) = rank (T*)$ . Deduce from (a) that $rank (TT *) = rank (T)$ .
3. (c) For any $n \times n$ matrix A, $rank (A * A) = rank (A A *) = rank (A)$ .
Let V be an inner product space, and let $y, z \in V$ . Define $T : V \to V$ by $T (x) = 〈 x, y 〉 z$ for all $x \in V$ . First prove that T is linear. Then show that T* exists, and find an explicit expression for it.

The following definition is used in Exercises 15-17 and is an extension of the definition of the adjoint of a linear operator.

Definition.

Let $T : V \to W$ be a linear transformation, where V and W are finite-dimensional inner product spaces with inner products ${〈 \cdot, \cdot 〉}_{1}$ and ${〈 \cdot, \cdot 〉}_{2}$ , respectively. A function $T * : W \to V$ is called an adjoint of T if ${〈 T (x), y 〉}_{2} = {〈 x, T * (y) 〉}_{1}$ for all $x \in V$ and $y \in W$ .

Let $T : V \to W$ be a linear transformation, where V and W are finite-dimensional inner product spaces with inner products ${〈 \cdot, \cdot 〉}_{1}$ and ${〈 \cdot, \cdot 〉}_{2}$ , respectively. Prove the following results.
1. (a) There is a unique adjoint T* of T, and T* is linear.
2. (b) If $β$ and $γ$ are orthonormal bases for V and W, respectively, then ${[T *]}_{γ}^{β} = ({[T]}_{β}^{γ}) *$ .
3. (c) $rank (T *) = rank (T) .$
4. (d) ${〈 T * (x), y 〉}_{1} = {〈 x, T (y) 〉}_{2}$ for all $x \in W$ and $y \in V$ .
5. (e) For all $x \in V, T * T (x) = 0$ if and only if $T (x) = 0$ .
State and prove a result that extends the first four parts of Theorem 6.11 using the preceding definition.
Let $T : V \to W$ be a linear transformation, where V and W are finite-dimensional inner product spaces. Prove that ${(R (T *))}^{⊥} = N (T)$ , using the preceding definition.
† Let A be an $n \times n$ matrix. Prove that $\det (A *) = \bar{\det (A)}$ . Visit goo.gl/csqoFY for a solution.
Suppose that A is an $m \times n$ matrix in which no two columns are identical. Prove that A* A is a diagonal matrix if and only if every pair of columns of A is orthogonal.
For each of the sets of data that follows, use the least squares approximation to find the best fits with both (i) a linear function and (ii) a quadratic function. Compute the error E in both cases.
1. (a) ${(- 3, 9), (- 2, 6), (0, 2), (1, 1)}$
2. (b) {(1, 2), (3,4), (5, 7), (7, 9), (9,12)}
3. (c) ${(- 2, 4), (- 1, 3), (0, 1), (1, - 1), (2, - 3)}$
In physics, Hooke’s law states that (within certain limits) there is a linear relationship between the length x of a spring and the force y applied to (or exerted by) the spring. That is, $y = c x + d$ , where c is called the spring constant. Use the following data to estimate the spring constant (the length is given in inches and the force is given in pounds).

Length x Force y

3.5 1.0

4.0 2.2

4.5 2.8

5.0 4.3
Find the minimal solution to each of the following systems of linear equations.
1. (a) $x + 2 y - z = 12$
2. (b) $\begin{array}{rcl} x + 2 y - z & = & 1 \\ 2 x + 3 y + z & = & 2 \\ 4 x + 7 y - z & = & 4 \end{array}$
3. (c) $\begin{array}{rcl} x + y - z & = & 0 \\ 2 x - y + z & = & 3 \\ x - y + z & = & 2 \end{array}$
4. (d) $\begin{array}{rrrrrrrcl} x & + & y & + & z & - & w & = & 1 \\ 2 x & - & y & + & w & = & 1 \end{array}$
Consider the problem of finding the least squares line $y = c t + d$ corresponding to the m observations $(t_{1}, y_{1}), (t_{2}, y_{2}), \dots, (t_{m}, y_{m})$ .
1. (a) Show that the equation $(A * A) x_{0} = A * y$ of Theorem 6.12 takes the form of the normal equations:
  
  $(\sum_{i = 1}^{m} t_{i}^{2}) c + (\sum_{i = 1}^{m} t_{i}) d = \sum_{i = 1}^{m} t_{i} y_{i}$
  
  and
  
  $(\sum_{i = 1}^{m} t_{i}) c + m d = \sum_{i = 1}^{m} y_{i} .$
  
  These equations may also be obtained from the error E by setting the partial derivatives of E with respect to both c and d equal to zero.
2. (b) Use the second normal equation of (a) to show that the least squares line must pass through the center of mass, $(\bar{t}, \bar{y})$ , where
  
  $\bar{t} = \frac{1}{m} \sum_{i = 1}^{m} t_{i} and \bar{y} = \frac{1}{m} \sum_{i = 1}^{m} y_{i} .$
Let V and ${e_{1}, e_{2}, \dots}$ be defined as in Exercise 23 of Section 6.2. Define $T : V \to V$ by

$T (σ) (k) = \sum_{i = k}^{\infty} σ (i) for every positive integer k .$

Notice that the infinite series in the definition of T converges because $σ (i) \neq 0$ for only finitely many i.
1. (a) Prove that T is a linear operator on V.
2. (b) Prove that for any positive integer n, $T (e_{n}) = \sum_{i = 1}^{n} e_{i} .$
3. (c) Prove that T has no adjoint. Hint: By way of contradiction, suppose that T* exists. Prove that for any positive integer n, $T * (e_{n}) (k) \neq 0$ for infinitely many k.

Length `x`	Force `y`
3.5	1.0
4.0	2.2
4.5	2.8
5.0	4.3

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 6.3 The Adjoint of a Linear Operator

Create new playlist

Sign In

Sign Up

Table of Contents for
6.3 The Adjoint of a Linear Operator