10
Introduction to Mathematical Statistics
10.1 Introduction and Four Data Sets
Before studying empirical models and then parametric models, we review some concepts from mathematical statistics. Mathematical statistics is a broad subject that includes many topics not covered in this chapter. For those topics that are covered, it is assumed that you have had some prior exposure. The topics of greatest importance for constructing actuarial models are estimation and hypothesis testing. Because the Bayesian approach to statistical inference is often either ignored or treated lightly in introductory mathematical statistics texts and courses, it receives more in-depth coverage in this text, in Chapter 13. Bayesian methodology also provides the basis for the credibility methods covered in Chapter 16.
To see the need for methods of statistical inference, consider the case where your supervisor needs a model for basic dental payments. One option is to simply announce the model. You proclaim that it is the lognormal distribution with 
and 
. (The many decimal places are designed to give your proclamation an aura of precision.) When your supervisor, a regulator, or an attorney who has put you on the witness stand, asks you how you know that to be so, it will likely not be sufficient to answer that “I just know these things,” “trust me, I am a trained statistician,” “it is too complicated, you wouldn't understand,” or “my friend at Gamma Dental uses that model.”
An alternative is to collect some data and use it to formulate a model. Most distributional models have two components. The first is a name, such as “Pareto.” The second is the set of parameter values that complete the specification. Matters would be simpler if modeling could be done in that order. Most of the time, we need to fix the parameters that go with a named model before we can decide if we want to use that model.
Because the parameter estimates are based on a sample from the population and not the entire population, the results will not be the true values. It is important to have an idea of the potential error. One way to express this error is with an interval estimate. That is, rather than announcing a particular value, a range of plausible values is presented.
When named parametric distributions are used, the parameterizations used are those from Appendices A and B.
Alternatively, you may want to construct a nonparametric model (also called an empirical model), where the goal is to determine a model that essentially reproduces the data. Such models are discussed in Chapter 14.
At this point we present four data sets, referred to as Data Sets A, B, C, and D. They will be used several times, both in this chapter and in later chapters.
Data Set A This data set is well known in the casualty actuarial literature. It was first analyzed in the paper [30] by Dropkin in 1959. From 1956 to 1958, he collected data on the number of accidents by one driver in one year. The results for 94,935 drivers are shown in Table 10.1.
Table 10.1 Data Set A.
| Number of accidents | Number of drivers |
| 0 | 81,714 |
| 1 | 11,306 |
| 2 | 1,618 |
| 3 | 250 |
| 4 | 40 |
| 5 or more | 7 |
Data Set B These numbers (and those in the next two data sets) are artificial. They represent the amounts paid on workers compensation medical benefits but are not related to any particular policy or set of policyholders. These payments are the full amount of the loss. A random sample of 20 payments is given in Table 10.2.
Table 10.2 Data Set B.
| 27 | 82 | 115 | 126 | 155 | 161 | 243 | 294 | 340 | 384 |
| 457 | 680 | 855 | 877 | 974 | 1,193 | 1,340 | 1,884 | 2,558 | 15,743 |
Data Set C These observations represent payments on 227 claims from a general liability insurance policy. The data are shown in Table 10.3.
Table 10.3 Data Set C.
| Payment range | Number of payments |
| 0–7,500 | 99 |
| 7,500–17,500 | 42 |
| 17,500–32,500 | 29 |
| 32,500–67,500 | 28 |
| 67,500–125,000 | 17 |
| 125,000–300,000 | 9 |
| Over 300,000 | 3 |
Data Set D This data set is from the experience of five-year term insurance policies. The study period is a fixed time period. The columns are interpreted as follows: (1) i is the policy number, 1–40; and (2) 
is the time since issue to when the insured was first observed. Thus, policies 1–30 were observed from when the policy was sold. The remaining policies were issued prior to the start of the observation period and were known to be alive at that duration. (3) 
is the time since issue to when the insured was observed to die. Those who were not observed to die during the five years have “—” in that column. (4) 
is the latest time since issue at which those who were not observed to die were observed. That could be because they surrendered their policy before the five years elapsed, reached the end of the five-year term, or the study ended while the policy was still in force. The data are shown in Table 10.4.
Table 10.4 Data Set D.
| i |  |
 |
 |
i |  |
 |
 |
| 1 | 0 | — | 0.1 | 16 | 0 | 4.8 | — |
| 2 | 0 | — | 0.5 | 17 | 0 | — | 4.8 |
| 3 | 0 | — | 0.8 | 18 | 0 | — | 4.8 |
| 4 | 0 | 0.8 | — | 19–30 | 0 | — | 5.0 |
| 5 | 0 | — | 1.8 | 31 | 0.3 | — | 5.0 |
| 6 | 0 | — | 1.8 | 32 | 0.7 | — | 5.0 |
| 7 | 0 | — | 2.1 | 33 | 1.0 | 4.1 | — |
| 8 | 0 | — | 2.5 | 34 | 1.8 | 3.1 | — |
| 9 | 0 | — | 2.8 | 35 | 2.1 | — | 3.9 |
| 10 | 0 | 2.9 | — | 36 | 2.9 | — | 5.0 |
| 11 | 0 | 2.9 | — | 37 | 2.9 | — | 4.8 |
| 12 | 0 | — | 3.9 | 38 | 3.2 | 4.0 | — |
| 13 | 0 | 4.0 | — | 39 | 3.4 | — | 5.0 |
| 14 | 0 | — | 4.0 | 40 | 3.9 | — | 5.0 |
| 15 | 0 | — | 4.1 |
10.2 Point Estimation
10.2.1 Introduction
Regardless of how a model is estimated, it is extremely unlikely that the estimated model will exactly match the true distribution. Ideally, we would like to be able to measure the error we will be making when using the estimated model. But doing so is clearly impossible! If we knew the amount of error we had made, we could adjust our estimate by that amount and then have no error at all. The best we can do is discover how much error is inherent in repeated use of the procedure, as opposed to how much error we made with our current estimate. Therefore, we are concerned about the quality of the ensemble of answers produced from the procedure, not about the quality of a particular answer.
This is a critical point with regard to actuarial practice. What is important is that an appropriate procedure be used, with everyone understanding that even the best procedure can lead to a poor result once the random future outcome has been revealed. This point is stated nicely in a Society of Actuaries principles draft [115, pp. 779–780] regarding the level of adequacy of a provision for a portfolio of life insurance risk obligations (i.e. the probability that the company will have enough money to meet its contractual obligations):
The indicated level of adequacy is prospective, but the actuarial model is generally validated against past experience. It is incorrect to conclude on the basis of subsequent experience that the actuarial assumptions were inappropriate or that the indicated level of adequacy was overstated or understated.
When constructing models, there are several types of error. Some, such as model error (choosing the wrong model) and sampling frame error (trying to draw inferences about a population that differs from the one sampled), are not covered here. An example of model error is selecting a Pareto distribution when the true distribution is, or is close to, Weibull. An example of sampling frame error is sampling claims from insurance policies that were sold by independent agents to price policies that are to be sold over the internet.
The type of error that we can measure is that resulting from using a sample from the population to make inferences about the entire population. Errors occur when the items sampled do not represent the population. As noted earlier, we cannot know if the particular items sampled today do or do not represent the population. We can, however, estimate the extent to which estimators are affected by the possibility of a nonrepresentative sample.
The approach taken in this chapter is to consider all the samples that might be taken from the population. Each such sample leads to an estimated quantity (e.g. a probability, a parameter value, or a moment). We do not expect the estimated quantities to always match the true value. For a sensible estimation procedure, we do expect that for some samples the quantity will match the true value, for many it will be close, and for only a few it will be quite different. If we can construct a measure of how well the set of potential estimates matches the true value, we have a handle on the quality of our estimation procedure. The approach outlined here is often called the classical or frequentist approach to estimation.
Finally, we need a word about the difference between estimate and estimator. The former refers to the specific value obtained when applying an estimation procedure to a set of numbers. The latter refers to a rule or formula that produces the estimate. An estimate is a number or function, while an estimator is a random variable or a random function. Usually, both the words and the context will make the reference clear.
10.2.2 Measures of Quality
10.2.2.1 Introduction
There are a variety of ways to measure the quality of an estimator. Three of them are discussed here. Two examples are used throughout to illustrate them.
Both examples are clearly artificial in that we know the answers prior to sampling (4.5 and 
). However, that knowledge will make apparent the error in the procedure we select. For practical applications, we need to be able to estimate the error when we do not know the true value of the quantity being estimated.
10.2.2.2 Unbiasedness
When constructing an estimator, it would be good if, on average, the errors we make were to cancel each other out. More formally, let 
be the quantity we want to estimate. Let 
be the random variable that represents the estimator and let 
be the expected value of the estimator 
when 
is the true parameter value.
The bias depends on the estimator being used and may also depend on the particular value of 
.
For Example 10.2, we have two estimators (the sample mean and 1.2 times the sample median) that are both unbiased. We will need additional criteria to decide which one we prefer.
Some estimators exhibit a small amount of bias, which vanishes as the sample size goes to infinity.
A drawback to unbiasedness as a measure of the quality of an estimator is that an unbiased estimator may often not be very close to the parameter, as would be the case if the estimator has a large variance. We will now demonstrate that there is a limit to the accuracy of an unbiased estimator in general, in the sense that there is a lower bound (called the Cramèr–Rao lower bound) on its variance.
In what follows, suppose that 
has joint pf or pdf 
, where 
. In the i.i.d. special case 
, where 
is the common pf or pdf of the 
. Of central importance in many discussions of parameter estimation is the score function, 
. We assume regularity conditions on g that will be discussed in detail later, but at this point we assume that g is twice differentiable with respect to 
and that the order of differentiation and expectation may be interchanged. In particular, this excludes situations in which an end point of the distribution depends on 
.
As is clear from the above example, U is a random function of 
(i.e. U is a random variable and a function of 
).
In the i.i.d. special case, let 
for 
, implying that 
are i.i.d. Then, 
.
We now turn to the evaluation of the mean of the score function. In the discrete case (the continuous case is similar),
The last step follows because the sum of the probabilities over all possible values must be 1.
Also,
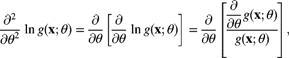
and so, by the quotient rule for differentiation,
Taking expectations yields
The first term is on the right-hand side is zero and therefore
Alternatively, using the definition of U, we have
Recall that 
. Then,
Before proceeding, we digress to note that, for any two random variables 
and 
,
To see that this is true, let 
, 
, 
, and 
. Then,
Note that this development also proves that 
.
Now let 
be an unbiased estimator of 
. Then, by the definition of unbiasedness,
and differentiating with respect to 
yields (recalling our assumption that the order of differentiation and summation/integration may be interchanged)
Then,
We next have
This implies that
In the i.i.d. case, 
, where 
and X is a generic version of the 
. Then, (10.1) becomes
Generally, the version using second partial derivatives (rather than the square of the first derivative) is easier to calculate.
The lower bounds (10.1) and (10.2) are often referred to as Cramèr–Rao lower bounds for the variance of unbiased estimators. This is extremely valuable for maximum likelihood and other estimation procedures. The denominators in each case are referred to as the Fisher or expected information.
10.2.2.3 Consistency
Another desirable property of an estimator is that it works well for extremely large samples. Slightly more formally, as the sample size goes to infinity, the probability that the estimator is in error by more than a small amount goes to zero. A formal definition follows.
A sufficient (although not necessary) condition for weak consistency is that the estimator be asymptotically unbiased and 
[equivalently, from (10.3), the mean squared error goes to zero as 
].
10.2.2.4 Mean Squared Error
While consistency is nice, most estimators have this property. What would be truly impressive is an estimator that is not only correct on average but comes very close most of the time and, in particular, comes closer than rival estimators. One measure for a finite sample is motivated by the definition of consistency. The quality of an estimator could be measured by the probability that it gets within 
of the true value – that is, by measuring 
. But the choice of 
is arbitrary, and we prefer measures that cannot be altered to suit the investigator's whim. Then we might consider 
, the average absolute error. But we know that working with absolute values often presents unpleasant mathematical challenges, and so the following has become widely accepted as a measure of accuracy.
Note that the MSE is a function of the true value of the parameter. An estimator may perform extremely well for some values of the parameter but poorly for others.
A result that follows directly from the various definitions is
If we restrict attention to only unbiased estimators, the best such estimator could be defined as follows.
Because we are looking only at unbiased estimators, it would have been equally effective to formulate the definition in terms of MSE. We could also generalize the definition by looking for estimators that are uniformly best with regard to MSE, but the previous example indicates why that is not feasible. There are some results that can often assist with the determination of UMVUEs (e.g. Hogg et al. [56, ch. 7]). However, such estimators are often difficult to determine. Nevertheless, MSE is still a useful criterion for comparing two alternative estimators.
For this example, the regularity conditions underlying the derivation of the Cramèr–Rao lower bound do not hold and so (10.2) cannot be used to set a minimum possible value.
10.2.3 Exercises
- 10.1 For Example 10.1, show that the mean of three observations drawn without replacement is an unbiased estimator of the population mean, while the median of three observations drawn without replacement is a biased estimator of the population mean.
- 10.2 Prove that, for random samples, the sample mean is always an unbiased estimator of the population mean.
- 10.3 Let X have the uniform distribution over the range
. That is, 
, 
. Show that the median from a sample of size 3 is an unbiased estimator of 
. - 10.4 Explain why the sample mean may not be a consistent estimator of the population mean for a Pareto distribution.
- 10.5 For the sample of size 3 in Exercise 10.3, compare the MSE of the sample mean and median as estimates of
. - 10.6 (*) You are given two independent estimators of an unknown quantity
. For estimator A, 
and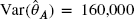 
, while for estimator B, 
and 
. Estimator C is a weighted average, 
. Determine the value of w that minimizes 
. - 10.7 (*) A population of losses has a Pareto distribution (see Appendix A) with
and 
unknown. Simulation of the results from maximum likelihood estimation based on samples of size 10 has indicated that 
and 
. Determine 
if it is known that 
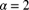. - 10.8 (*) Two instruments are available for measuring a particular nonzero distance. The random variable X represents a measurement with the first instrument and the random variable Y one with the second instrument. Assume that X and Y are independent with
, 
, 
, and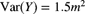 
, where m is the true distance. Consider estimators of m that are of the form 
. Determine the values of 
and 
that make Z a UMVUE within the class of estimators of this form. - 10.9 A population contains six members, with values 1, 1, 2, 3, 5, and 10. A random sample of size 3 is drawn without replacement. In each case, the objective is to estimate the population mean. Note: The use of a spreadsheet with an optimization routine may be the best way to solve this problem.
- Determine the bias, variance, and MSE of the sample mean.
- Determine the bias, variance, and MSE of the sample median.
- Determine the bias, variance, and MSE of the sample midrange (the average of the largest and smallest observations).
- Consider an arbitrary estimator of the form
, where 
are the sample order statistics.
- Determine a restriction on the values of a, b, and c that will assure that the estimator is unbiased.
- Determine the values of a, b, and c that will produce the unbiased estimator with the smallest variance.
- Determine the values of a, b, and c that will produce the (possibly biased) estimator with the smallest MSE.
- 10.10 (*) Two different estimators,
and 
, are being considered. To test their performance, 75 trials have been simulated, each with the true value set at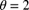 
. The following totals have been obtained:
where
is the estimate based on the jth simulation using estimator 
. Estimate the MSE for each estimator and determine the relative efficiency (the ratio of the MSEs). - 10.11 Consider an i.i.d. random sample
from the distribution with cdf 
, for 
and zero otherwise.
- Let
be an estimator of 
. Demonstrate that
- Determine the mean squared error of
, and demonstrate that it may be expressed in the form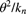 
, where 
is a positive integer. Also show that 
is a consistent estimator of 
. - Let
. Prove that 
is an unbiased and consistent estimator of 
. - Let
, where 
. Derive the expected value and mean squared error of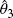 
, and explain why 
would generally be preferred to both 
and 
as an estimator of 
.
- Let
10.3 Interval Estimation
All of the estimators discussed to this point have been point estimators. That is, the estimation process produces a single value that represents our best attempt to determine the value of the unknown population quantity. While that value may be a good one, we do not expect it to match the true value exactly. A more useful statement is often provided by an interval estimator. Instead of a single value, the result of the estimation process is a range of possible numbers, any of which is likely to be the true value. A specific type of interval estimator is the confidence interval.
Note that this definition does not uniquely specify the interval. Because the definition is a probability statement and must hold for all 
, it says nothing about whether or not a particular interval encloses the true value of 
from a particular population. Instead, the level of confidence, 
, is a property of the method used to obtain L and U and not of the particular values obtained. The proper interpretation is that, if we use a particular interval estimator over and over on a variety of samples, at least 
of the time our interval will enclose the true value. Keep in mind that it is the interval end points that are random.
The construction of confidence intervals is usually very difficult. For example, we know that, if a population has a normal distribution with unknown mean and variance, a 
confidence interval for the mean uses
where 
and 
is the 
th percentile of the t distribution with b degrees of freedom. But it takes a great deal of effort to verify that (10.4) is correct (see, e.g. Hogg et al. [56, p. 186]).
However, there is a method for constructing approximate confidence intervals that is often accessible. Suppose that we have a point estimator 
of parameter 
such that 
, 
, and 
has approximately a normal distribution. Theorem 11.4 shows that these three properties are often the case. With all these approximations, we have that, approximately,
where 
is the 
th percentile of the standard normal distribution. Solving for 
produces the desired interval. It is sometimes difficult to obtain the solution (due to the appearance of 
in the denominator) and so, if necessary, replace 
in (10.5) with 
to obtain a further approximation:
10.3.1 Exercises
- 10.12 Let
be a random sample from a population with pdf 
, 
. This exponential distribution has a mean of 
and a variance of 
. Consider the sample mean, 
, as an estimator of 
. It turns out that 
has a gamma distribution with 
and 
, where in the second expression the “
” on the left is the parameter of the gamma distribution. For a sample of size 50 and a sample mean of 275, develop 95% confidence intervals by each of the following methods. In each case, if the formula requires the true value of 
, substitute the estimated value.
- Use the gamma distribution to determine an exact interval.
- Use a normal approximation, estimating the variance prior to solving the inequalities as in (10.6).
- Use a normal approximation, estimating
after solving the inequalities as in Example 10.14.
- 10.13 (*) A sample of 2,000 policies had 1,600 with no claims and 400 with one or more claims. Using the normal approximation, determine the symmetric 95% confidence interval for the probability that a single policy has one or more claims.
10.4 The Construction of Parametric Estimators
In previous sections, we developed methods for assessing the quality of an estimator. In all the examples, the estimators being evaluated were arbitrary, though reasonable. This section reviews two methods for constructing estimators. A third is covered in Chapter 11. In this section, we assume that n independent observations from the same parametric distribution have been collected. There are two, essentially incompatible, approaches to estimating parameters. This section and Chapter 11 cover the frequentist approach to estimation introduced in Section 10.2. An alternative estimation approach, known as Bayesian estimation, is covered in Chapter 13.
The methods introduced in Section 10.4.1 are relatively easy to implement but tend to give poor results. Chapter 11 covers maximum likelihood estimation. This method is more difficult to use but has superior statistical properties and is considerably more flexible.
10.4.1 The Method of Moments and Percentile Matching
Let the distribution function for an individual observation be given by
where 
is the transpose of 
. That is, 
is a column vector containing the p parameters to be estimated. Furthermore, let 
be the kth raw moment, and let 
be the 100gth percentile of the random variable. That is, 
. If the distribution function is continuous, there will be at least one solution to that equation.
For a sample of n independent observations from this random variable, let 
be the empirical estimate of the kth moment and let 
be the empirical estimate of the 100gth percentile.
The motivation for this estimator is that it produces a model that has the same first p raw moments as the data (as represented by the empirical distribution). The traditional definition of the method of moments uses positive integers for the moments. Arbitrary negative or fractional moments could also be used. In particular, when estimating parameters for inverse distributions, the matching of negative moments may be a superior approach.2
There is no guarantee that the equations will have a solution or, if there is a solution, that it will be unique.
The motivation for this estimator is that it produces a model with p percentiles that match the data (as represented by the empirical distribution). As with the method of moments, there is no guarantee that the equations will have a solution or, if there is a solution, that it will be unique. One problem with this definition is that percentiles for discrete random variables (such as the empirical distribution) are not always well defined. For example, Data Set B has 20 observations. Any number between 384 and 457 has 10 observations below and 10 above, and so could serve as the median. The convention is to use the midpoint. However, for other percentiles, there is no “official” interpolation scheme.3 The following definition is used here.
Unless there are two or more data points with the same value, no two percentiles will have the same value. One feature of this definition is that 
cannot be obtained for 
or 
. This seems reasonable, as we should not expect to be able to infer the value of very large or small percentiles from small samples. We use the smoothed version whenever an empirical percentile estimate is needed.
The estimates are much different from those obtained in Example 10.15, which is one indication that these methods may not be particularly reliable.
10.4.2 Exercises
- 10.14 Determine the method of moments estimate for a lognormal model for Data Set B.
- 10.15 (*) The 20th and 80th percentiles from a sample are 5 and 12, respectively. Using the percentile-matching method, estimate
assuming that the population has a Weibull distribution. - 10.16 (*) From a sample, you are given that the mean is 35,000, the standard deviation is 75,000, the median is 10,000, and the 90th percentile is 100,000. Using the percentile-matching method, estimate the parameters of a Weibull distribution.
- 10.17 (*) A sample of size 5 has produced the values 4, 5, 21, 99, and 421. You fit a Pareto distribution using the method of moments. Determine the 95th percentile of the fitted distribution.
- 10.18 (*) In year 1 there are 100 claims with an average size of 10,000 and in year 2 there are 200 claims with an average size of 12,500. Inflation increases the size of all claims by 10% per year. A Pareto distribution with
and 
unknown is used to model the claim size distribution. Estimate 
for year 3 using the method of moments. - 10.19 (*) From a random sample, the 20th percentile is 18.25 and the 80th percentile is 35.8. Estimate the parameters of a lognormal distribution using percentile matching and then use these estimates to estimate the probability of observing a value in excess of 30.
- 10.20 (*) A claim process is a mixture of two random variables A and B, where A has an exponential distribution with a mean of 1 and B has an exponential distribution with a mean of 10. A weight of p is assigned to distribution A and
to distribution B. The standard deviation of the mixture is 2. Estimate p by the method of moments. - 10.21 (*) A random sample of 20 observations has been ordered as follows:
Determine the 60th sample percentile using the smoothed empirical estimate.
- 10.22 (*) The following 20 wind losses (in millions of dollars) were recorded in one year:
Determine the sample 75th percentile using the smoothed empirical estimate.
- 10.23 (*) The observations 1,000, 850, 750, 1,100, 1,250, and 900 were obtained as a random sample from a gamma distribution with unknown parameters
and 
. Estimate these parameters by the method of moments. - 10.24 (*) A random sample of claims has been drawn from a loglogistic distribution. In the sample, 80% of the claims exceed 100 and 20% exceed 400. Estimate the loglogistic parameters by percentile matching.
- 10.25 (*) Let
be a random sample from a population with cdf 
. Determine the method of moments estimate of p. - 10.26 (*) A random sample of 10 claims obtained from a gamma distribution is given as follows:
Estimate
and 
by the method of moments. - 10.27 (*) A random sample of five claims from a lognormal distribution is given as follows:
Estimate
and 
by the method of moments. Estimate the probability that a loss will exceed 4,500. - 10.28 (*) The random variable X has pdf
. For this random variable, 
and 
. You are given the following five observations:
Determine the method of moments estimate of
. - 10.29 The random variable X has pdf
. It is known that 
. You are given the following five observations:
Determine the method of moments estimate of
. - 10.30 Use the data in Table 10.5 to determine the method of moments estimate of the parameters of the negative binomial model.
Table 10.5 The data for Exercise 10.30.
Number of claims Number of policies 0 9,048 1 905 2 45 3 2 4+ 0 - 10.31 Use the data in Table 10.6 to determine the method of moments estimate of the parameters of the negative binomial model.
Table 10.6 The data for Exercise 10.31.
Number of claims Number of policies 0 861 1 121 2 13 3 3 4 1 5 0 6 1 7+ 0 - 10.32 (*) Losses have a Burr distribution with
. A random sample of 15 losses is 195, 255, 270, 280, 350, 360, 365, 380, 415, 450, 490, 550, 575, 590, and 615. Use the smoothed empirical estimates of the 30th and 65th percentiles and percentile matching to estimate the parameters 
and 
. - 10.33 (*) Losses have a Weibull distribution. A random sample of 16 losses is 54, 70, 75, 81, 84, 88, 97, 105, 109, 114, 122, 125, 128, 139, 146, and 153. Use the smoothed empirical estimates of the 20th and 70th percentiles and percentile matching to estimate the parameters
and 
. - 10.34 (*) Losses follow a distribution with pdf
, 
. The sample mean is 300 and the sample median is 240. Estimate 
and 
by matching these two quantities.
10.5 Tests of Hypotheses
Hypothesis testing is covered in detail in most mathematical statistics texts. This review is fairly straightforward and does not address philosophical issues or consider alternative approaches. A hypothesis test begins with two hypotheses, one called the null and one called the alternative. The traditional notation is 
for the null hypothesis and 
for the alternative hypothesis. The two hypotheses are not treated symmetrically. Reversing them may alter the results. To illustrate this process, a simple example is used.
The decision is made by calculating a quantity called a test statistic. It is a function of the observations and is treated as a random variable. That is, in designing the test procedure, we are concerned with the samples that might have been obtained and not with the particular sample that was obtained. The test specification is completed by constructing a rejection region. It is a subset of the possible values of the test statistic. If the value of the test statistic for the observed sample is in the rejection region, the null hypothesis is rejected and the alternative hypothesis is announced as the result that is supported by the data. Otherwise, the null hypothesis is not rejected (more on this later). The boundaries of the rejection region (other than plus or minus infinity) are called the critical values.
The test in the previous example was constructed to meet certain objectives. The first objective is to control what is called the Type I error. It is the error made when the test rejects the null hypothesis in a situation in which it happens to be true. In the example, the null hypothesis can be true in more than one way. As a result, a measure of the propensity of a test to make a Type I error must be carefully defined.
This is a conservative definition in that it looks at the worst case. It is typically a case that is on the boundary between the two hypotheses.
The significance level is usually set in advance and is often between 1% and 10%. The second objective is to keep the Type II error (not rejecting the null hypothesis when the alternative is true) probability small. Generally, attempts to reduce the probability of one type of error increase the probability of the other. The best we can do once the significance level has been set is to make the Type II error as small as possible, though there is no assurance that the probability will be a small number. The best test is one that meets the following requirement.
Because the Type II error probability can be high, it is customary to not make a strong statement when the null hypothesis is not rejected. Rather than saying that we choose or accept the null hypothesis, we say that we fail to reject it. That is, there was not enough evidence in the sample to make a strong argument in favor of the alternative hypothesis, so we take no stand at all.
A common criticism of this approach to hypothesis testing is that the choice of the significance level is arbitrary. In fact, by changing the significance level, any result can be obtained.
Few people are willing to make errors 38.51% of the time. Announcing this figure is more persuasive than the earlier conclusion based on a 5% significance level. When a significance level is used, those interpreting the output are left to wonder what the outcome would have been with other significance levels. The value of 38.51% is called a p-value. A working definition follows.
Also, because the p-value must be between 0 and 1, it is on a scale that carries some meaning. The closer to zero the value is, the more support the data give to the alternative hypothesis. Common practice is that values above 10% indicate that the data provide no evidence in support of the alternative hypothesis, while values below 1% indicate strong support for the alternative hypothesis. Values in between indicate uncertainty as to the appropriate conclusion, and may call for more data or a more careful look at the data or the experiment that produced it.
This approach to hypothesis testing has some consequences that can create difficulties when answering actuarial questions. The following example illustrates these problems.
It is important to keep in mind that hypothesis testing was invented for situations in which collecting data was either expensive or inconvenient. For example, in deciding if a new drug cures a disease, it is important to confirm this fact with the smallest possible sample so that, if the results are favorable, the drug can be approved and made available. Or, consider testing a new crop fertilizer. Every test acre planted costs time and money. In contrast, in many types of actuarial problems, a large amount of data is available from historical records. In this case, unless the data follow a parametric model extremely closely, almost any model can be rejected by using a sufficiently large set of data.
10.5.1 Exercise
- 10.35 (Exercise 10.12 continued) Test
versus 
using a significance level of 5% and the sample mean as the test statistic. Also, compute the p-value. Do this twice, using: (i) the exact distribution of the test statistic and (ii) a normal approximation.