Appendix B
An Inventory of Discrete Distributions
B.1 Introduction
The 16 models presented in this appendix fall into three classes. The divisions are based on the algorithm used to compute the probabilities. For some of the more familiar distributions, these formulas will look different from the ones you may have learned, but they produce the same probabilities. After each name, the parameters are given. All parameters are positive unless otherwise indicated. In all cases, ![]() is the probability of observing k losses.
is the probability of observing k losses.
For finding moments, the most convenient form is to give the factorial moments. The jth factorial moment is ![]() . We have
. We have ![]() and
and ![]() .
.
The estimators presented are not intended to be useful estimators but, rather, provide starting values for maximizing the likelihood (or other) function. For determining starting values, the following quantities are used (where ![]() is the observed frequency at k [if, for the last entry,
is the observed frequency at k [if, for the last entry, ![]() represents the number of observations at k or more, assume it was at exactly k] and n is the sample size):
represents the number of observations at k or more, assume it was at exactly k] and n is the sample size):
When the method of moments is used to determine the starting value, a circumflex (e.g. ![]() ) is used. For any other method, a tilde (e.g.
) is used. For any other method, a tilde (e.g. ![]() ) is used. When the starting value formulas do not provide admissible parameter values, a truly crude guess is to set the product of all
) is used. When the starting value formulas do not provide admissible parameter values, a truly crude guess is to set the product of all ![]() and
and ![]() parameters equal to the sample mean and set all other parameters equal to 1. If there are two
parameters equal to the sample mean and set all other parameters equal to 1. If there are two ![]() or
or ![]() parameters, an easy choice is to set each to the square root of the sample mean.
parameters, an easy choice is to set each to the square root of the sample mean.
The last item presented is the probability generating function,
B.2 The (a,b,0) Class
The distributions in this class have support on ![]() . For this class, a particular distribution is specified by setting
. For this class, a particular distribution is specified by setting ![]() and then using
and then using ![]() . Specific members are created by setting
. Specific members are created by setting ![]() , a, and b. For any member,
, a, and b. For any member, ![]() , and for higher j,
, and for higher j, ![]() . The variance is
. The variance is ![]() .
.
B.2.1.1 Poisson – 

B.2.1.2 Geometric – 

This is a special case of the negative binomial with ![]() .
.
B.2.1.3 Binomial – 
(![]() , m an integer)
, m an integer)

B.2.1.4 Negative Binomial – 

B.3 The (a,b,1) Class
To distinguish this class from the ![]() class, the probabilities are denoted
class, the probabilities are denoted ![]() or
or ![]() . depending on which subclass is being represented. For this class,
. depending on which subclass is being represented. For this class, ![]() is arbitrary (i.e. it is a parameter), and then
is arbitrary (i.e. it is a parameter), and then ![]() or
or ![]() is a specified function of the parameters a and b. Subsequent probabilities are obtained recursively as in the
is a specified function of the parameters a and b. Subsequent probabilities are obtained recursively as in the ![]() class:
class: ![]() ,
, ![]() , with the same recursion for
, with the same recursion for ![]() . There are two subclasses of this class. When discussing their members, we often refer to the “corresponding” member of the
. There are two subclasses of this class. When discussing their members, we often refer to the “corresponding” member of the ![]() class. This refers to the member of that class with the same values for a and b. The notation
class. This refers to the member of that class with the same values for a and b. The notation ![]() will continue to be used for probabilities for the corresponding
will continue to be used for probabilities for the corresponding ![]() distribution.
distribution.
B.3.1 The Zero-Truncated Subclass
The members of this class have ![]() , and therefore it need not be estimated. These distributions should only be used when a value of zero is impossible. The first factorial moment is
, and therefore it need not be estimated. These distributions should only be used when a value of zero is impossible. The first factorial moment is ![]() , where
, where ![]() is the value for the corresponding member of the
is the value for the corresponding member of the ![]() class. For the logarithmic distribution (which has no corresponding member),
class. For the logarithmic distribution (which has no corresponding member), ![]() . Higher factorial moments are obtained recursively with the same formula as with the
. Higher factorial moments are obtained recursively with the same formula as with the ![]() class. The variance is
class. The variance is ![]() . For those members of the subclass that have corresponding
. For those members of the subclass that have corresponding ![]() distributions,
distributions, ![]() .
.
B.3.1.1 Zero-Truncated Poisson – 

B.3.1.2 Zero-Truncated Geometric – 

This is a special case of the zero-truncated negative binomial with ![]() .
.
B.3.1.3 Logarithmic – 

This is a limiting case of the zero-truncated negative binomial as ![]() .
.
B.3.1.4 Zero-Truncated Binomial – 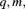
(![]() , m an integer)
, m an integer)

B.3.1.5 Zero-Truncated Negative Binomial – 

This distribution is sometimes called the extended truncated negative binomial distribution because the parameter r can extend below zero.
B.3.2 The Zero-Modified Subclass
A zero-modified distribution is created by starting with a truncated distribution and then placing an arbitrary amount of probability at zero. This probability, ![]() , is a parameter. The remaining probabilities are adjusted accordingly. Values of
, is a parameter. The remaining probabilities are adjusted accordingly. Values of ![]() can be determined from the corresponding zero-truncated distribution as
can be determined from the corresponding zero-truncated distribution as ![]() or from the corresponding
or from the corresponding ![]() distribution as
distribution as ![]() . The same recursion used for the zero-truncated subclass applies.
. The same recursion used for the zero-truncated subclass applies.
The mean is ![]() times the mean for the corresponding zero-truncated distribution. The variance is
times the mean for the corresponding zero-truncated distribution. The variance is ![]() times the zero-truncated variance plus
times the zero-truncated variance plus ![]() times the square of the zero-truncated mean. The probability generating function is
times the square of the zero-truncated mean. The probability generating function is ![]() , where
, where ![]() is the probability generating function for the corresponding zero-truncated distribution.
is the probability generating function for the corresponding zero-truncated distribution.
The maximum likelihood estimator of ![]() is always the sample relative frequency at zero.
is always the sample relative frequency at zero.
B.4 The Compound Class
Members of this class are obtained by compounding one distribution with another. That is, let N be a discrete distribution, called the primary distribution, and let ![]() be i.i.d. with another discrete distribution, called the secondary distribution. The compound distribution is
be i.i.d. with another discrete distribution, called the secondary distribution. The compound distribution is ![]() . The probabilities for the compound distributions are found from
. The probabilities for the compound distributions are found from

for ![]() , where a and b are the usual values for the primary distribution (which must be a member of the
, where a and b are the usual values for the primary distribution (which must be a member of the ![]() class) and
class) and ![]() is
is ![]() for the secondary distribution. The only two primary distributions used here are Poisson (for which
for the secondary distribution. The only two primary distributions used here are Poisson (for which ![]() ) and geometric [for which
) and geometric [for which ![]() ]. Because this information completely describes these distributions, only the names and starting values are given in the following sections.
]. Because this information completely describes these distributions, only the names and starting values are given in the following sections.
The moments can be found from the moments of the individual distributions:
The pgf is ![]() .
.
In the following list, the primary distribution is always named first. For the first, second, and fourth distributions, the secondary distribution is the ![]() class member with that name. For the third and the last three distributions (the Poisson–ETNB and its two special cases), the secondary distribution is the zero-truncated version.
class member with that name. For the third and the last three distributions (the Poisson–ETNB and its two special cases), the secondary distribution is the zero-truncated version.
B.4.1 Some Compound Distributions
B.4.1.1 Poisson–Binomial – 
(![]() , m an integer)
, m an integer)
B.4.1.2 Poisson–Poisson – 
The parameter ![]() is for the primary Poisson distribution, and
is for the primary Poisson distribution, and ![]() is for the secondary Poisson distribution. This distribution is also called the Neyman Type A:
is for the secondary Poisson distribution. This distribution is also called the Neyman Type A:
B.4.1.3 Geometric–Extended Truncated Negative Binomial – 
The parameter ![]() is for the primary geometric distribution. The last two parameters are for the secondary distribution, noting that for
is for the primary geometric distribution. The last two parameters are for the secondary distribution, noting that for ![]() the secondary distribution is logarithmic. The truncated version is used so that the extension of r is available.
the secondary distribution is logarithmic. The truncated version is used so that the extension of r is available.
B.4.1.4 Geometric–Poisson – 
B.4.1.5 Poisson–Extended Truncated Negative Binomial – 
When ![]() the secondary distribution is logarithmic, resulting in the negative binomial distribution.
the secondary distribution is logarithmic, resulting in the negative binomial distribution.
or,

where
This distribution is also called the generalized Poisson–Pascal.
This is a special case of the Poisson–extended truncated negative binomial with ![]() . It is actually a Poisson–truncated geometric.
. It is actually a Poisson–truncated geometric.
This is a special case of the Poisson–extended truncated negative binomial with ![]() .
.
B.5 A Hierarchy of Discrete Distributions
Table B.1 indicates which distributions are special or limiting cases of others. For the special cases, one parameter is set equal to a constant to create the special case. For the limiting cases, two parameters go to infinity or zero in some special way.
Table B.1 The hierarchy of discrete distributions.
| Distribution | Is a special case of | Is a limiting case of |
| Poisson | ZM Poisson | Negative binomial, |
| Poisson–binomial, | ||
| Poisson–inverse Gaussian, | ||
| Polya–Aeppli, | ||
| Neyman–Type A | ||
| ZT Poisson | ZM Poisson | ZT negative binomial |
| ZM Poisson | ZM negative binomial | |
| Geometric | Negative binomial | Geometric–Poisson |
| ZM geometric | ||
| ZT geometric | ZT negative binomial | |
| ZM geometric | ZM negative binomial | |
| Logarithmic | ZT negative binomial | |
| ZM logarithmic | ZM negative binomial | |
| Binomial | ZM binomial | |
| Negative binomial | ZM negative binomial | Poisson–ETNB |
| Poisson–inverse Gaussian | Poisson–ETNB | |
| Polya–Aeppli | Poisson–ETNB | |
| Neyman–Type A | Poisson–ETNB |
