+ 6 +

Mathematical Communities

What sorts of communities do mathematicians form? How do their communities shape their lives? We will describe some informal groups, which were formed around specific needs of their participants. Whether inside or outside universities, communities that were fueled by a shared vision have brought about significant change in mathematics.

Insiders and Outsiders

Stan Ulam has written:

Much of the historical development of mathematics has taken place in specific centers. These centers, large or small, have formed around a single person or a few individuals, and sometimes as a result of the work of a number of people—a group in which mathematical activity flourished. Such a group possesses more than just a community of interests; it has a definite mood and character in both the choice of interests and the method of thought. . . . The great nineteenth-century centers such as Göttingen, Paris and Cambridge (England) all exercised their own peculiar influence on the development of mathematics.¹

In this chapter we will look at three 20th century communities based in university mathematics departments: Göttingen in Germany, from the 1890s to the 1930s; its New York offspring, the Courant Institute, starting in the 1930s; and the Department of Mechanics and Mathematics (Mekh-Mat) at Moscow State University in its “golden age” of the 1960s. Göttingen and Moscow are tragic examples, showing the fragility of intellectual communities under hostile regimes.

We also look at four communities that are intentional rather than organizational, established by people with a strong common goal or interest who did not find any existing organization to serve their purpose. One example was the Jewish People’s University in Moscow from 1978 to 1983. Another was the Anonymous Group in Budapest, led by Paul Erdős. A more famous example was the French group Bourbaki. Originally inspired by a desire to renew and modernize French mathematics, it later focused on producing a series of texts, held together by a common vision of what mathematics could or should be (formal, axiomatic, abstract) and a rebellious or combative attitude toward the classical French mathematical program of analytic function theory.

Our last example is a contemporary group, the Association for Women in Mathematics (AWM). It provides a meeting place for female mathematicians and students, whose members work and fight to improve their status and recognition. (Membership is not restricted to women and there are male members as well.) It is a community of practice and belief. It has a lot in common with the National Association of Mathematicians (NAM), which addresses the needs and concerns of African-American mathematicians and mathematics students. There is also a group of Chicano and Native American mathematicians—The Society of Chicanos and Native Americans in Science (SACNAS)—but it is not devoted solely to mathematics. These contemporary communities are greatly assisted by electronic communication, as well as face-to-face meetings, and are comparable to the Anonymous Group and Bourbaki in being autonomous, self-created communities based on a common interest.

Clearly there are many overlapping interacting mathematical communities of various sizes, kinds, lifetimes. There are research communities, there are publishing communities, there are teaching communities, and there are even bureaucratic communities (for example, the groups of mathematicians associated with the National Science Foundation). One can think of the whole mathematical community as the union of all these smaller subcommunities.

Active researchers are always to some degree members of communities in certain subject areas. Some researchers, like Kurt Gödel and Andrew Wiles, have been private, even secretive for a while; others, like Bill Thurston and Paul Erdős, have been outgoing and communicative; but in either case, the research is motivated and ultimately evaluated by a community of some kind, whether face to face or electronic. The membership list in such a community is less definite, membership is a matter of degree; it may be variable or even controversial.

The historian David Rowe has written:

A fundamentally new type of mathematical community has now rendered the traditional nineteenth-century modes of communication and invention largely obsolete. Mathematics today is essentially an oral culture; to keep abreast of it one must attend conferences and workshops, or, better yet, be associated with a leading research center where the latest developments from near and afar are constantly being discussed. By the time an important result actually appears in print today, it is probably no longer new; in any case, it will probably be impossible to understand the work without the aid of an “interventer” who already knows the thrust of the argument through an oral source.²

In the 20 years since Rowe wrote this, e-mail networks have again transformed mathematical communication and made it much more rapid. His point about the need to be “plugged into the loop” in order to keep up with current research is much more valid today.

At the American Institute of Mathematics in Palo Alto, California, focused workshops are held throughout the year. Several mathematicians interested in a common problem are invited to meet each other there and spend a week in concentrated joint effort.

A totally new form of mathematical collaboration was started in February 2009 by Timothy Gowers of Cambridge University in England, whose work in combinatorics has won him a Fields Medal. He called it the Polymath Project. A carefully chosen problem was proposed for public access on the Web: “to find an elementary proof of a special case of the density Hales-Jewett theorem (DHJ), which is a central result of combinatorics.” Anyone who wanted to join in could post suggestions or calculations toward solving the problem. The results were indeed impressive. A major open problem was solved in a few weeks by the shared effort of over two dozen contributors from several countries. Gowers wrote:

When the collaborative discussion kicked off on February 1, it started slowly; more than seven hours passed before Jozsef Solymosi, a mathematician at the University of British Columbia in Vancouver, made the first comment. Fifteen minutes later a comment came in from Arizona-based high-school teacher Jason Dyer. Three minutes after that Terence Tao (winner of a Fields Medal, the highest honour in mathematics) at the University of California, Los Angeles, made a comment. Over the next 37 days, 27 people contributed approximately 800 substantive comments, containing 170,000 words. . . . Progress came far faster than anyone expected. On March 10, Gowers announced that he was confident that the Polymath participants had found an elementary proof of the special case of DHJ, but also that, very surprisingly, the argument could be straightforwardly generalized to prove the full theorem.³

Where is the emotional side of this? Any community has members and nonmembers. To be a community means to include and to exclude. Membership provides rights and privileges. Exclusion withholds some or all of those rights and privileges. There might be some persons who would like to be included but who are excluded. So, of course, inclusion or exclusion from a community has an emotional side. Inclusion brings security and solidarity. Exclusion, for good reason or bad, may provoke resentment and hostility.

Ideally, access to the mathematics community would be based solely on mathematical merit. If you are a creative mathematician, if you solve hard problems or invent interesting concepts, you should be welcome. And by and large, that is pretty much true.

On the other hand, things aren’t always that simple. The mathematical community never did exist in a vacuum. Somebody has to pay the bills. The money has to come from somewhere. As we will see in this chapter, attached to the money may be values and prejudices—political prejudices, nationalist prejudices, religious prejudices, race prejudices, gender prejudices, and age prejudices. The price paid for being female by Sophie Germain, Sonia Kovalevskaya, and Emmy Noether is discussed in the next chapter. Issues of race, language, nationality, and ideology are also relevant, as during the Cold War. Age can be a problem too, if one is too young or too old (see chapter 7).

Some people have found entry into the mathematical community a challenging and at times discouraging process. The famous mathematical statistician Herbert Robbins was asked, “Were there any mathematicians who gave you guidance and encouragement during critical periods of your professional development?” He answered, “No. What they gave me was something perhaps more important. The leading mathematicians I encountered made me want to tell them, ‘You son-of-a-bitch, you think that you’re smart and I’m dumb. I’ll show you that I can do it too!’ It was like being the new kid in the neighborhood. You go out into the street and the first guy you meet walks up to you and knocks you down. Well, that’s not exactly guidance or encouragement. But it has an effect.” But in the same interview Robbins also said, “Marston Morse impressed me deeply. I could see that he was on fire with creation. . . . He was, in a way, the type of person I would like to have been.”⁴

Some stories of pathos, incomplete promise, and exclusion are famous among mathematicians and have been told in Eric Temple Bell’s much-read Men of Mathematics. Evariste Galois (1811–1832) died before he was 21 in a stupid, meaningless duel. He had already been noticed and marked as a brilliant young mathematician. On his own, he had penetrated to the heart of the theory of polynomials—the algebra of permutations of the roots, which we now call Galois theory. But this was at the time of the restoration of the Bourbon monarchy in France, which followed the French Revolution in the late 18th century. Galois’ father sided with the Revolution; he was actually driven to suicide by persecution from Royalists and priests. Young Evariste was a revolutionary firebrand. In his own lifetime, his profound and transformative contribution to algebra was neither accepted nor understood. He was an outsider to the mathematical establishment, which was then dominated by the great and famous Augustin-Louis Cauchy (1789–1857), a most pious, reverent Royalist and Catholic.

In the same era, Niels Abel (1802–1829) was also outstandingly brilliant, both in the field of polynomial equations and in the blossoming field of analytic function theory. He had the misfortune to be Norwegian, and therefore a foreigner and outsider to the mathematical grandees in Berlin and Paris. After great efforts to obtain some recognition, a professorship was finally offered to him. But by the time the offer arrived, he had died of tuberculosis exacerbated by overwork and poverty.

Bourbaki

One very influential group that started outside the mathematical establishment was Bourbaki. In 1934, a group of young mathematicians met for lunch in the Latin Quarter in Paris, at the cafe “A Capoulade,” at 63 boulevard Saint-Michel, on the corner with rue Soufflot. (The café has since been replaced by an American fast-food outlet.) The group started as a project by André Weil and Claude Chevalley to rewrite the obsolete analysis text of Edouard Jean-Baptiste Goursat (1858–1936) (We recount the early career of André Weil in chapter 3.) Chevalley was a devotee of avant-garde art and a member of an anarchist grouplet. They had a concrete project in mind: “to define for 25 years the syllabus for the certificate in differential and integral calculus by writing, collectively, a treatise on analysis.”⁵ Early additions to the group were Jean Dieudonné, Henri Cartan, and Jean Delsarte. Dieudonné became the secretary of the group. They whimsically decided to give their group a name, “Nicolas Bourbaki,” a fictitious person who would become a famous “mathematician.”

For decades every word published by Bourbaki received its final editing from the pen of Dieudonné. He was notoriously big, loud, and dogmatic. He not only remembered every word, he even remembered on what page every word had appeared. Another member, Henri Cartan, would become one of the major mathematicians of his time, specializing in Lie groups, functions of several complex variables, and coauthoring with Sammy Eilenberg the first major exposition of category theory. His father was the famous geometer Élie Cartan. Élie’s father, Henri’s grandfather, was a blacksmith.

Their objective soon became much more ambitious: to renew and modernize French mathematics, which they viewed as stuck in the classical French tradition focused on analytic function theory. Jacques Dieudonné wrote:

The First World War was a dreadful hecatomb of young French scientists. When we open the war-time directory of the École Normale, we find enormous gaps which signify that two-thirds of the ranks were mowed down by the war. This situation had unfortunate repercussions for French mathematics. We others, too young to have been in direct contact with the war, but entering the University in the years after the war ended, should have had as our guides these young mathematicians, certain of whom we are sure would have had great futures. These were the young men who were brutally decimated and whose influence was destroyed. Obviously, people of previous generations were left, great scholars whom we all honor and respect were living and still extremely active, but these mathematicians were nearly fifty years old, if not older. There was a generation between them and us. It is indubitable that a 50-year-old mathematician knows the mathematics he learned at 20 or 30, but has only notions, often rather vague, of the mathematics of his epoch, i.e., the period of time when he is 50. It is a fact we have to accept such as it is, we cannot do anything about it. [In 1970, when this article was published, Dieudonné was 64.] So we had excellent professors to teach us the mathematics of let us say up to 1900, but we did not know very much about the mathematics of 1920. The German mathematics school in the years following the war had a brilliance which was altogether exceptional . . . of whom we in France knew nothing. Not only this, but we also knew nothing of the rapidly developing Russian school, the brilliant Polish school, which had just been born, and many others. We knew neither the work of F. Riesz nor that of von Neumannn. The only exception was Élie Cartan; but being 20 years ahead of his time, he was understood by no one.⁶

Weil and Chevalley sought to emulate the spirit of the modern abstract algebra then being born at Göttingen under the leadership of Emmy Noether. The great textbook Moderne Algebra was written by the Dutch mathematician B. L. Van der Waerden with the participation of Emil Artin in the spirit of Emmy Noether. Van Der Waerden’s book is a masterpiece of organization and conciseness. Everything is stated exactly when and where needed, nothing has to be repeated, and there’s no need to refer to any other book. This style became the ideal of Bourbaki: complete rigor, complete self-containment, avoidance of unnecessary comments or explanations and any use of diagrams or illustrations, or use of geometric thinking. And rigorous avoidance of any contact with physics!

At the beginning they met monthly. They wanted to write collectively, and they aimed to introduce each topic with a general notion such as “field, operation, set, or group.” Henri Cartan later wrote that the time appeared ripe for a comprehensive study of all important branches of mathematics, assuming nothing as given and making the basic interrelationships comprehensible, and so he and his friends decided to take this task upon themselves. He admitted that only the young could make such a bold decision. They were not unaware of the difficulties involved. Indeed, such an undertaking lay far beyond the powers of a single person. It would necessarily be a communal effort.

Figure 6-1. Heinrich Behnke and Henri Cartan. Courtesy of Ludwig Danzer.

They did not opt for the usual division of labor, where each person writes on a single specialty. Instead, the entire group discussed each topic. This led to long debates, and in the end it was impossible to determine who had written what. The work became a collective effort in the true sense. The members brought in ideas and methods they had acquired abroad. They were teaching in provincial universities, which helped them to think independently of the centralized Parisian establishment. They consciously opposed existing institutions. They met outside the university, and they chose a publisher (Hermann) who at that time was marginal to the mathematicians who dominated the field.

Nevertheless, these men were an elite group in a highly hierarchical system, aspiring to the leadership of French mathematics. In fact, within 30 years Bourbaki became dominant in French mathematics, and very influential in many other countries. Their style and taste not only became standard for much advanced research, it even seeped down into college, secondary, and primary education. The “new math” project in the United States, known as the School Mathematics Study Group (SMSG), was one ramification of Bourbaki. In November 1959, at the Cercle Culturel de Royaumont, at Asnieres-sur-Oise, in France, at a conference on reforming French math education, Dieudonné rose to his feet with the cry, “A bas Euclide! Mort aux triangles!” (“Down with Euclid! Death to triangles!”) Their idea was to throw geometry out of high schools and replace it with linear algebra. Dieudonné was by then over 50 and no longer an active member of Bourbaki.

The president of the Royaumont conference, and one of the guiding sprits of the new math, was Marshall Stone of the University of Chicago. Stone beautifully summarized his point of view by saying that a modern mathematician would characterize his subject as “the study of general abstract systems, each one of which is built of specified abstract elements and structured by the presence of arbitrary but unambiguously specified relations among them.” This abstractionist credo of Stone’s is a perfect summary of Bourbaki’ism.

Figure 6-2. Jean Dieudonné of Bourbaki. Courtesy of Archives of the Mathematisches Forschungsinstitut Oberwolfach.

Bourbaki excluded any applied mathematics, and it totally ignored and avoided physics. Weil had lived in Göttingen in 1926, when the world of physicists there was bubbling with excitement as they gave birth to quantum mechanics. Yet, as he later wrote, he didn’t notice what was going on around him at all.

The first volume in the Bourbaki series, Elements of Mathematics, came out in 1939, but then their meetings were disrupted by World War II. After the war, they published one or two volumes every year until 1983. Some volumes were quite long. The early volumes were about set theory, algebra, general topology, elementary calculus, and integration theory. At the beginning many members opposed including the topic of mathematical logic. Chevalley managed to change their minds. Later volumes treated Lie groups and commutative algebra. As Cartan described their working methods in the 1950s, members met three times a year at so-called Bourbaki congresses. Eight to 12 participants would gather in a quiet place far removed from the noise of the cities. Two meetings lasted a week, the third, during the summer vacation, lasted 14 days. They worked on average 7 or 8 hours a day; the rest of the time they walked and dined. It was not uncommon for all the participants to start talking at the same time.

The writing of these volumes could go through six or eight drafts, each draft written by a different author. Treatments of important topics were changed after sustained debates. Dieudonné wrote in 1970:

Even when two men have a 20-year age difference, this does not stop the younger from hauling the elder, who he feels has understood nothing of the question, over the coals. One has to know how to take it, as one should, with a smile. . . . Certain foreigners, invited as spectators to Bourbaki meetings, always come out with the impression that it is a gathering of madmen. They could not imagine how these people shouting—sometimes three or four at the same time—about mathematics, could ever come up with something intelligent. . . . When we have seen the same chapter come back six, seven, eight or ten times, everybody is so sick of it that there is a unanimous vote to send it to press. . . . We are concerned then with replacing members affected by the age limit. . . . A youth of value who shows promise of a great future is quickly noticed. When this happens, he is invited to attend one of the Congresses as a guinea pig . . . the wretched young man is subjected to the ball of fire which constitutes a Bourbaki discussion. Not only must he understand, but he must also participate. If he is silent, he is simply not invited again.⁷

The deadly solemnity of their textbooks gives no hint of the carefree gaiety of their meetings with each other. When their semiregular publication of Elements of Mathematics became a commercial success, the royalties paid for travel expenses, wine, and extracurricular activities that enlivened the proceedings. According to La Tribu, their internal newsletter, they played chess, table soccer, volleyball, or Frisbee. They went on mountain hikes, bicycle excursions, and swimming expeditions and even caroused in bumper cars. They went butterfly hunting or mushroom picking. They sunbathed, stuffed themselves with local delicacies, and drank until royally drunk—Armagnac, champagne, rum toddies, or wine. It was even reported that, once they had swallowed enough wine, members had been seen doing a virile French can-can or a lascivious belly dance.

Cartan emphasized that the close collaboration of Bourbaki required a feeling of community and friendship, complete candor, and good spirits, with each individual suspending his egotism for the good of the group. In a study of collaborative circles, the sociologist Michael Ferrell stresses the roles of thoughtful critics and enthusiastic audiences. Together with many others who have written about collaboration, he emphasizes that the most important feature is trust. The mathematicians who formed Bourbaki provided these resources for each other. They were patient listeners and powerful debaters, and they were remarkably able to sustain the vision that linked them.

The participants also thought carefully about how to keep group cohesion without sacrificing the freshness of new contributions. They established a rule that a member had to leave at age 50, so there was a succession of four generations of Bourbaki. The “alumni” remained identified with the group, even as they went on to high visibility as individuals in national and international mathematical establishments. The former outsiders became powerful insiders! The rise of the antiestablishment Bourbaki founders to become the establishment troubled some of them. But for years they stuck to the tasks ahead of them and ignored their internal tensions about the group’s power and prestige.

Chevalley, the anarchist, was asked how it felt to have participated in a project that ultimately led to taking power. He answered that he felt a lot of resentment toward the members who produced this outcome. At the start, the congresses were paid for out of the members’ pockets. But later, there were very substantial royalties. That was one cause of the degeneration. Then, before the war, it had been understood that one did not talk about career matters; “it was simply not done.” But after the war, when they began to bring in young people, they naturally felt concerned about their careers. Little by little, they talked of everyone’s career. The last straw, he said, was Dieudonné’s propagandizing for mathematical reform.

As the group reached the fourth generation, the common focus and working style weakened, and members became more specialized in their interests. By the end of the 1970s, the style of Bourbaki had been so well propagated and understood that everyone knew how to write in this spirit. At this stage the group had run its course. Rather than initiating new works, the members decided to revise and update their previous volumes.

Alexandre Grothendieck, whose life we describe in chapter 4, was in the third generation of Bourbaki. In Récoltes et Semailles he wrote:

It was certainly during the sixties that Bourbaki’s “tone” slipped to increasingly prominent elitism, a change in which I surely took part. . . . I still remember my astonishment when I discovered in 1970 the extent to which Bourbaki was unpopular among the lower strata . . . of the mathematical world. The name had become more or less a synonym for elitism, for strict dogmatism, for a cult that favored “canonicalism” at the expense of living comprehension, for hermetism, for castrating antispontaneity, and that’s not even all! . . . This group of exceptional quality exists no more. I don’t know when it died, for it surely died without anyone noticing and sounding its death knell, not even within his heart of hearts. I suppose that an imperceptible degradation occurred in the members—everyone must have “got on in years,” must have gone stale. They became important, prominent, powerful, feared, sought-after. Perhaps the spark remains, but innocence was lost along the way. . . . And respect was also lost along the way. When we had students, perhaps it was too late for the best to be passed on—there was still the spark, but there was no longer innocence.⁸

In 1997 Pierre Cartier, a third-generation member, was asked why Bourbaki had published nothing new since 1983. He blamed a clash between Bourbaki and their publisher about royalties and translation rights that ended in a long, unpleasant lawsuit. But he added that the 1980s were a natural limit. After all, André Weil had insisted that every member should retire at 50, and so it made sense that Bourbaki also should retire when it reached 50. But the main reason, he thought, was that Bourbaki had achieved its stated goal: to provide foundations for all existing mathematics.

Cartier analyzed the ascent and decline of Bourbaki in terms of ideology; they resembled other strong ideologies of the 20th century whose leaders also believed in their limitless future.

Bourbaki was to be the New Euclid, he would write a textbook for the next 2,000 years. . . . It is no accident that Bourbaki lasted from the beginning of the thirties to the eighties, while the Soviet system lasted from 1917 to 1989. The 20th century has been a century of ideology, the ideological age. When I began in mathematics the main task of a mathematician was to bring order and make a synthesis of existing material, to create what Thomas Kuhn called normal science. . . . Now we are again at the beginning of a new revolution. Mathematics is undergoing major changes. We don’t know exactly where it will go, it is not yet time to make a synthesis of all these things—maybe in twenty or thirty years it will be time for a new Bourbaki. I consider myself very fortunate to have had two lives. A life of normal science and a life of scientific revolution.⁹

From a different perspective, one can compare Bourbaki’s approach with that of logical positivism, a philosophy holding that metaphysical and subjective arguments not based on observable data are meaningless. Members in both of these thought communities fought for consistency, rigor, clarity, and intellectual boundaries. Their emphasis on pure rationality contrasted sharply with the chaotic world around them.

In analyzing scientific discoveries, biologist Ludvik Fleck described how division of labor, cooperation, preparatory work, technical assistance, mutual exchange of ideas, and controversy can produce a collective that contains much more knowledge than any one individual. But together with all of the advantages of a socially organized style of knowing, Fleck also describes how thought collectives can become rigid and resistant to new discoveries. In Bourbaki a similar growth and decline can be noted. They started as rebels against the established modes of thought in French mathematics in the early 20th century. As a carefully organized group, they were successful in developing a rigorous systemization of their field. But with new discoveries and the increasingly important interaction between physics and mathematics, their exclusionist approach lost its effectiveness. Contemporary mathematics is more multifaceted, it includes more varied theoretical and applied approaches. Bourbaki remains a fascinating example of a disciplined group effort to achieve intellectual transformation.

As our next example of a voluntary mathematical community, we describe the Anonymous Group, led by Paul Erdős in Budapest in the 1930s.

The Anonymous Group

The Hungarian mathematician, Paul Erdős, was legendary for his friendships and collaborations. Already as a young university student he met weekly in a park in Budapest with about 10 young people. Their meeting place was next to a statue of a 15th century historian whose name was not known; thus he and the Erdős group were called “Anonymous.” One member, George Szekeres, who became a major Australian mathematician, remembered those meetings with great affection: “We met perhaps once a week and tried to go through the problems in a well-known book. These were collections of problems from mathematical analysis, and we tried to solve the problems, one after the other. It was a marvelous experience, I must say.”

The group included several young women. One of them, Esther Klein, made an important contribution to the group when she brought to their attention a class of problems that later were known as “Ramsey theory.” (At first they didn’t know that such questions had previously been considered by Frank Ramsey in England.) In the simplest case of a Ramsey-type question, we consider a party with six guests. Then it’s not too hard to prove that either there are three guests all of whom are already acquainted with each other, or else there are three guests no two of whom are previously acquainted. The numbers get much worse when you have more guests at the party. Szekeres was intrigued by the way in which Esther, his future wife, asked the question. He could solve the first part of the problem, after some struggle, but part of it is still unsolved. Erdős named this problem “the Happy Ending” because of Szekeres’s and Klein’s marriage. Szekeres and Klein fled from the Nazis to Australia, by way of Siberia and Shanghai. There they were able to inspire Hungarian-type problem contests.

The group members were all interested in problems of discrete mathematics—combinatorics, graph theory, and number theory. They first became acquainted with each other through the Mathematics Journal for Secondary Schools, which published challenging problems in each issue and listed the names and photographs of successful problem solvers.

As a result of the Great Depression and the quotas excluding Jewish academics, not one of these young mathematicians had a regular job. Erdős’s parents were both gymnasium (high school) math teachers, and they could set up tutoring jobs for them. The members of the Anonymous Group included Pál Turán, Tibor Gallai, and George Szekeres, who would all become leading mathematicians in their own right—and Erdős’s first collaborators. Other members were Márta Wachsberger, Géza Grünwald (1910–1943), Anna Grünwald, András Vázsonyi, Annie Beke, Dénes Lazar, Esther (Eppie) Klein, and László Alpár.

Alpár went to France. There he was imprisoned as a Communist. When he was released at the end of World War II, he came home to Communist Hungary and was imprisoned again, under the Stalinist regime. After coming out of jail for the second time, he took up mathematics full time for the first time.

Turán served in a Fascist labor camp during World War II. Before and after that, he had a brilliant research career. At the time of his death in 1976, he had become a major figure in international mathematics. We quoted his account of doing mathematics in a labor camp in chapter 3.

Alpár, Erdős, Szekeres, and Klein had left Hungary before the Holocaust. Of those who had remained, only Vázsonyi, Gallai, and Turán survived.

Göttingen

Göttingen is far from the German capital Berlin; it is an idyllic little town on the slopes of the Hainberg. Its university was founded in 1737 by George II August, the Prince-Elector of Hannover and King of England, and so it’s sometimes called “the Georgia Augusta.” In 1866, when Hannover and its ally Austria were defeated in war by Prussia, Göttingen became part of Prussia. It was in Göttingen that the prince of mathematicians, Carl Friedrich Gauss, served for decades as director of the observatory. Gauss was followed by his devoted colleague Peter Gustave Lejeune Dirichlet. Georg Friedrich Bernhard Riemann, Gauss’s student and Dirichlet’s friend, was the third great mathematician who worked in Göttingen. But Gauss, Dirichlet, and Riemann had few pupils. They were not surrounded by a genuine mathematical community.

It was the wunderkind Felix Klein who conceived of creating a multidisciplinary scientific center at Göttingen. Klein had been a full professor at Erlangen at the unheard of early age of 23. Students today learn about his Erlangen program, in which he unified and classified all geometries by their symmetry groups. In 1881 and 1882 Klein competed intensely with Henri Poincaré to develop the theory of automorphic functions. He wrote much later:

The price I had to pay for my work was extraordinarily high—my health completely collapsed. In the next years I had to take long leaves and to renounce all productive activity. Things did not go well again until the autumn of 1884; but I have never regained my earlier level of productivity. I never returned to elaborate my earlier ideas. And later, when I was at Göttingen, I turned to extending the domain of my work and to general tasks of organizing our science. . . . My real productive activity in theoretical mathematics perished in 1882. All that has followed, insofar as it has not been purely expository, has been merely a matter of working out details.¹⁰

After he recovered from his breakdown, Klein was still a great teacher and expositor, but more than that, he became the eminence grise, the power broker and deal maker of German mathematics. Through a close friendship with Friedrich Althoff, the head of the Prussian system of higher education, from the 1880s to his death in the 1920s, Klein had a major say in who was appointed to what mathematics position in German universities.

Having in mind the growing needs of German industry and science, Klein imagined Göttingen as a different kind of mathematics center, one where mathematicians would welcome interaction with physics and engineering, even with biology and philosophy. It would provide an alternative to Berlin, where, under the control of the analyst Karl Weierstrass, the algebraist F. Georg Frobenius, and the number theorists Leopold Kronecker and Ernst Eduard Kummer, mathematics was pure.

David Hilbert epitomized Klein’s notion of the kind of mathematician Germany needed. He joined the faculty at Göttingen in 1895. His personality, his scholarship, and his unusual breadth as a mathematician became the central core of one of the most outstanding mathematical communities in history. His first great contributions to mathematical research were in algebraic number theory. Then he turned to the foundations of geometry, to integral equations, to relativity theory, and to logic and the foundations of mathematics. In each area he made fundamental contributions that transformed the field. In each area he stimulated younger people to make their own important contributions. The full story of Göttingen is told in Constance Reid’s books.

In his “Reminiscences from Hilbert’s Göttingen,” Richard Courant wrote:

If you read old chronicles, a Göttingen professor was a demi-god and very rank-conscious—the professor, and particularly the wife of the professor. Hilbert came to Göttingen and it was very, very upsetting. Some of the older Professors’ wives met and said: “Have you heard about this new mathematician who has come? He is upsetting the whole situation here. I learned that the other night he was seen in some restaurant, playing billiards in the back room with Privat dozents.” [The Privat dozent was lower than an “instructor” today, for he was paid nothing by the university; he received only whatever fees he could collect directly from his students.] It was considered completely impossible for a full professor to lower himself to be personally friendly with younger people. But Hilbert broke this tradition completely, and this was an enormous step toward creating scientific life; young students came to his house and had tea or dinner with him. Frau Hilbert gave big lavish dinner-parties for assistants, students etc. Hilbert went with his students, and also everybody else who wanted to come, for hour-long hikes in the woods during which mathematics, politics and economics were discussed.

One could also go and visit Hilbert in his garden. He spent his whole time gardening and in between gardening and little chores, he went to a long blackboard, maybe twenty feet long, covered so that also in the rain he could walk up and down, doing his mathematics in between digging some flower beds. All day one could observe him.

. . . He was a uniquely inspiring lecturer. . . . You had the chance to observe him struggling with sometimes very simple questions of mathematics, and finding his way out. This was more inspiring than a wonderfully perfect performance lecturing. The most impressive thing was the great variety, the wide spectrum of his interests. . . . He was a most concrete, intuitive mathematician who invented, and very consciously used, a principle: namely, if you want to solve a problem first strip the problem of everything that is not essential. Simplify it, specialize it as much as you can without sacrificing its core. Thus it becomes simple, as simple as it can be made, without losing any of its punch, and then you solve it. The generalization is a triviality which you don’t have to pay too much attention to. This principle of Hilbert’s proved extremely useful for him and also for others who learned it from him; unfortunately it has been forgotten.¹¹

Hilbert was open to problems and ideas from everywhere, open to colleagues from other disciplines, and open to students from Hungary, America, Russia, and Japan. Hermann Minkowski and David Hilbert were fascinated by Einstein’s theory of relativity, and Minkowski gave relativity theory its interpretation as a four-dimensional space-time manifold. Emmy Noether, the prime creator of modern abstract algebra, was fully accepted in Hilbert’s research community, even as the academic bureaucracy denied her as a woman any of the recognition that would have been appropriate to her scientific stature. Grace Chisholm came from England. John Pierpont Morgan and later Willard Van Orman Quine and Saunders MacLane came from the United States. We will focus on three participants whose lives are not as widely known as those of Hilbert and Courant: Teiji Takagi, Fritz John, and Kurt Friedrichs.

One of the most interesting visitors to Göttingen was Teiji Takagi (1875–1960), a brilliant mathematics student in Tokyo. In May 1898, Takagi received the following writ from the minister of education: “You are ordered to go to Germany in order to study mathematics for three years.” Japan was still in an early stage of westernization in the late 19th century, and when Takagi was “ordered” to go study in Europe, it was a very high honor for a young Japanese scholar.

In the spring of 1900, after three semesters in Berlin, Takagi dropped in at Göttingen, where a friend was studying. Takagi was attracted by the work of Hilbert and changed his schedule to include a long stay in Göttingen. Takagi later wrote, “I was much astonished by the striking contrast in the atmospheres of the mathematics departments of Göttingen and of Berlin. In the former, once a week a meeting was held, and in attendance was a group of brilliant youths from all over the world, as if here were the center of the mathematical world.”¹² This was unlike Berlin, which was more traditional.

In his book, Theory of Algebraic Number Fields, Hilbert had suggested that the “relatively Abelian fields” might be the most fascinating objects in this area, containing hidden, beautiful general laws. This book became the bible in Takagi’s mathematical life. (Hilbert himself had already moved on, to study integral equations.) In Göttingen, Takagi made some progress on his project and published about it. He stayed in Germany for 5 years. Then he went home, married, became a very prestigious Japanese mathematics professor, and had six children. But he needed stimulation to be productive. In Japan there was no one to talk to about algebraic number theory. When World War I started, it became even worse, for now he no longer even received mathematical journals from Germany. Yet, strangely enough, this intensified isolation somehow did stimulate him! During the war, totally cut off from all research contact, he produced two great papers on “class field theory.” Within a few years, his ideas came to be understood and appreciated in Europe. The key event was when Carl Ludwig Siegel (1896–1981), a German mathematician specializing in number theory, showed Takagi’s work to his famous colleague Emil Artin.

Figure 6-3. Taiji Takagi, Japanese algebraic number theorist. Courtesy of Ioan James.

In 1932 Takagi was sent to Europe as a delegate of the Science Council of Japan. In Vienna, Olga Taussky welcomed him and invited him to dinner at her apartment several times, providing him a warm reception with her mother and sister. In Hamburg, his student Shokichi Iyanaga introduced him to Emil Artin, and Takagi impressed Artin as being a modest but great scholar. Artin’s wife, Natascha, later wrote, “I liked Takagi very much.” In Göttingen, Takagi, accompanied by Emmy Noether, visited his master, Hilbert, who was struggling with liver disease. Takagi wrote, “Observing my old master grumbling as if speaking to himself, I wept in my heart.” At the International Congress in Zurich, Takagi was one of the vice presidents. At this Congress, the award called the Fields Medal was established, with five judges including Takagi.

In the Hotel Eden by Lake Zurich, where Takagi was staying, he held a dinner party on September 11 or 12 which he later described as one of the best times in his long life. He wrote to his wife in Japan about this party, telling her how he had specially selected the wines to be served. The guests were Chevalley, Helmut Hasse, Shokichi Iyanaga, Y. Mimura and his wife, M. Moriya, M. Nagano, Emmy Noether, Olga Taussky, N. G. Chebotaryev, and B. L. van der Waerden. We can only speculate that Takagi’s delight in assembling these famous mathematicians around one table may be related to his long periods of isolation from stimulating colleagues in his home country.

Two months later, the Nazis became the number one party in Germany. In 1934 Olga Taussky went to England and then in 1947 to the United States. Takagi survived the bombing and invasion of Japan. After World War II, the first letter to Takagi from abroad came from Olga, asking about his safety. Takagi passed away peacefully on February 28 in 1960, at the age of 84. About 1000 people attended his funeral.

One important visitor to Göttingen in the 1920s was the Russian topologist Pavel Sergeevich Aleksandrov (1896–1982), later head of the graduate math program during the “golden years” at Moscow State University. Aleksandrov wrote that one attractive feature of Courant’s mathematical institute was the close relationships of its members, who were really woven into a single team. (In 1922 Courant founded the university’s Mathematics Institute, although the building was not formally dedicated until 1929.) He further pointed out, although Courant’s program was mainly directed towards mathematical physics, Emmy Noether’s school of abstract algebra was far from applications. Nevertheless, both schools were closely linked by friendly connections between their members. These two schools, taken together, he thought, determined the face of Göttingen mathematics. He wrote of “their common enthusiasm, their unselfish love of mathematics, their awareness of its perfection as a striking creation of human thought and, following from this perfection, its inevitable unity. The idea of the uniqueness and intrinsic perfection of mathematics, and its unlimited cognitive force, which is necessarily directed towards the good of mankind, were Hilbert’s credo as a scientist,” said Aleksandrov, “and also the credo of the Courant and Noether schools.”¹³

The great period of Göttingen was divided into two parts by World War I. The comfortable, prosperous times before the war became much harder in the years after 1918. At the university mess hall, soups and stews were ladled from a long trough, and students flirted with serving girls in the hope of getting larger portions. Constantly thinking about food made it hard to concentrate on their books. Yet the intellectual life was intense and idealistic, struggling for a firm position on the problems of the times—political, philosophical, religious, humanistic, artistic, and literary.

Two Göttingen students of the 1920s, Kurt Friedrichs and Fritz John, would become well-known, influential American mathematicians in the 1950s and 1960s. Kurt Friedrichs arrived at Göttingen as a young student in 1922. He was overwhelmed by the superior knowledge of the young lecturers and assistants at Göttingen, “such a bunch of people who knew everything about everything.” He was captivated by the informal, exciting atmosphere around Courant. Even though Friedrichs was very retiring (not much at ease with himself or the rest of the world), Courant quickly recognized his gift. “I think it took keen observation as well as a really intense human interest on Courant’s part to see what was there,” said another of Courant’s famous students.¹⁴

Even after Friedrichs had published several works and had several more awaiting publication, Courant admitted that Friedrichs still made a somewhat poor first impression. But in 1930 the Technische Hochschule in Braunschweig appointed Friedrichs to a full professorship.

Fritz John arrived at Göttingen in 1929. He wrote:

I arrived there as an almost pennyless student, with money scraped together by my hard working widowed mother. . . . I managed to survive due to the fact that some of the faculty extended a helping hand. . . . Practice sessions gave students an opportunity to come to the attention of the faculty. With Courant’s help I obtained a stipend from the Studienstiftung des Deutschen Volkes, which relieved me of my main financial worries. Courant’s lack of pomposity and his concern with students set an example to the faculty. Students whom he considered promising could count on his help, were invited to his house, and if suitable, participated in the musical activities of his family. He unselfishly strove to advance the cause of mathematics, though he undoubtedly enjoyed being in the center of things. . . . [Gustav] Herglotz gave beautifully polished lectures, seemingly on any subject under the sun, from celestial mechanics to geometry of numbers. In the course of time I attended many of his lectures and fell under his spell. . . . Sometimes his ethereal way of proving things in his lectures completely hid some simple direct access to the same result. One could only admire, but without hope of entering on one’s own, this fantastic world of beauty, with its 19th century flavor. . . . Courant’s course was the exact opposite. Courant’s lectures lacked the glamour of those of Herglotz and of Hermann Weyl. They were, however, deeply stimulating, and offered a chance to participate in the creative process.¹⁵

These happy years were terminated by the rise of Hitler. Courant was Jewish. His heroic war record for Germany in World War I made no difference; he was kicked out of the institute he led in Göttingen. So were the great number theorist Edmund Landau and Felix Bernstein, the professor of statistics. Bernstein had once been vice-president of the local branch of the German Democratic Party, but he had given up politics when his support for the Weimar Republic hurt his standing in the academic community.

Among the many foreign visitors to Göttingen, several of the most famous were Jewish: the Swiss Paul Bernays, the Ukrainian Alexander Ostrowski, the Hungarians Theodor von Kármán and John von Neumann. Four German members—Richard Courant, Ernst Hellinger, Max Born, and Otto Toeplitz—came from Breslau. Every one of these names became illustrious. Bernays became Hilbert’s assistant and collaborator in mathematical logic. Von Kármán became one of the preeminent founders of modern aeronautics. Von Neumann, of course, was legendary, one of the true icons of modern mathematics. All were driven away.

But there had been a long history of antagonism in the university faculty between the liberal, cosmopolitan physicists and mathematicians and the nationalistic, reactionary faction that dominated the “humanist” faculties. The town itself was historically right-wing politically. A few faculty members like Bernstein had ventured into liberal or socialist politics, earning the lasting hatred of their opponents. By the end of the 1920s the student body was dominated by anti-Semitic and Nazi factions.

In Göttingen there was a large group of students around Hilbert who, as Courant wrote, really lived in complete dedication to the task of learning and studying. They were closely connected to each other and had much contact with the faculty. They spent a lot of time debating scientific and philosophical matters and trying to solve the mysteries of life. But the number of students increased, and gradually class distinction grew between those who had contact with assistants and the faculty and an anonymous mass of people who felt excluded. Courant thought that this certainly had something to do with the success of the Nazis. “The disenfranchised students who studied but didn’t get anywhere saw others invited to dinner in the houses of the professors and included in swimming parties with the assistants and felt that they ‘did not belong.’ They formed, gradually, a large body of dissatisfied, sometimes quite intelligent elements. When the Nazis came, this was a wonderful reservoir for them. . . . In 1933 suddenly, to the great surprise of the faculty and older students, in many of the classes and in the seminars and at the university institutions, students turned up—but you didn’t really know them—with the insignia of the Nazi party.”¹⁶

When Courant was dismissed from his post as director of the Mathematics Institute, he was replaced by Helmut Hasse. A famous number theorist, Hasse was not a Nazi, merely a right-wing nationalist quite willing to serve the Nazis. He met suspicion and opposition from the student Nazi faction who wanted a real Nazi as director. At first the Hilberts spoke out against the new regime, and their friends remaining in Göttingen were frightened for their safety. But Hilbert and his wife didn’t trust many of the people who were left, nor the new people who came, so after a while they too were silent.

The lives of Fritz John and Kurt Friedrichs were profoundly changed by the new policies of the German Reich. John’s father was Jewish. His fiancée, Charlotte Woellmer, was not Jewish. Ten days after he received his Ph.D., he and Charlotte got married, not knowing whether it was still legal or safe to enter into a “mixed” marriage. They had to involve their families as little as possible, and there were anonymous denunciations against them. They felt trapped, with the door slowly closing. Finally, in the fall of 1933, Courant managed to secure a scholarship for John at Cambridge, and he emigrated to England safely in January. Charlotte followed 2 months later.

Friedrichs had no Jewish parent, but days after Hitler became chancellor he attended a ball in Brauschweig—the social event of the year—looking for a young Jewish girl he had noticed on the way home from his morning lecture. When he spotted her dark, straight hair, bobbed like that of the American movie actress Colleen Moore, he marched across the ballroom and invited Nellie Bruell to dance. Thus began the romance of his life.

In 1935 Friedrichs managed to visit Courant in New York. Courant promised to look for a job for him in the United States, no easy task at a time when many American Ph.D.’s couldn’t find jobs. While Friedrichs was on his way home, the Nuremberg laws were passed, forbidding marriage between Aryans and non-Aryans. For a whole year, he and Nellie met infrequently and secretly. In 1936 he left Germany, allowed to take only 10 deutsch marks out of the country. To protect his parents, he told them nothing about his plans. Nellie had a French passport, and as soon as Friedrichs was safely out of Germany, she left for her father’s home in Lyons. Friedrichs arrived in New York penniless. Courant found him a place to live, and Nellie came to join him. As soon as they could find a justice of the peace, they were married. Her outgoing, supportive nature and her talent for friendship perfectly complemented his needs.

After 1934 Hilbert stopped teaching but continued to work on logic. His friends and collaborators emigrated. His Collected Works appeared in 1935. He lived on in Göttingen, isolated from the international world of mathematics and suffering progressive loss of memory. In 1942 he fell and broke his arm. He died on February 14, 1943, of complications from the physical inactivity that resulted from the accident. Only a dozen people attended the funeral.

The Courant Institute

When Richard Courant, the leader and organizer of mathematics at Göttingen in the late 1920s and early 1930s was driven away, he went first to Cambridge and then to New York. There he established a graduate program at New York University (NYU) in the spirit of Göttingen, which during and after World War II became a leading world center of applied mathematics. One of the authors of this book, Reuben Hersh, is a graduate of that program. When I applied for admission as a graduate student in mathematics to New York University in the spring of 1957, I was interviewed by a soft-spoken man with a slight German accent. His name was Fritz John. After learning about my dubious qualifications, he suggested that I take advanced calculus during the summer. If I did all right, I could become a grad student in the fall. That fall, as a full-time graduate student in mathematics, I enrolled in Introduction to Applied Mathematics taught by Professor Cathleen Morawetz, who was the daughter of the well-known applied mathematician J. L. Synge.

Figure 6-4. Cathleen Morawetz (center), winner of the National Medal of Science, with colleagues. Courtesy of Sylvia Wiegand.

I had the good luck to have Fritz John as my professor in a course on complex variables. A couple of years later, while about halfway through my grad student career, one evening before going home from NYU’s Mathematics Institute, I walked around the corner to La Maison Francaise, to hear a performance of Schubert’s Trout Quintet. The room at La Maison Francaise was full. It felt like a salon, with an intense connection between listeners and performers. It was one of the most powerful musical experiences I have ever encountered.

The piano was played by Lenny Sarason, a fellow graduate student at the institute. Sarason had earned a master’s degree under the composer Paul Hindemith before turning to mathematics. (Later we would share an office for a year as instructors at Stanford.) The violist was Lori Berkowitz, wife of one of my professors, Jerry Berkowitz, and daughter of the director of the institute, Richard Courant. The cellist was Jürgen Moser, Courant’s son-in-law by way of Courant’s other daughter. Moser would later become famous for contributions to celestial mechanics and dynamical systems.

The family atmosphere at the Mathematics Institute (renamed the Courant Institute when Courant retired a few years later) was not just a matter of chamber music. It also extended to a deep concern for the welfare of the students. Professor Bob Richtmyer’s wife, Jane, was in charge of payroll. Once, when some foul-up delayed the teaching assistants’ and research assistants’ monthly checks, and I had the audacity to complain, Jane offered me a loan from her personal bank account. A needy graduate student I knew was helped by the institute, which hired his wife part-time for the electrical engineering group. Later, when it was rumored that he might leave for a better paying job, his pay was raised.

However, this warm family atmosphere was not enjoyed by all the students at the institute. There were insiders and outsiders. Many students were part-timers, taking one or two courses toward a master’s degree while working at an electronics firm in New Jersey or Long Island. Such a student might feel left out when he noticed another student exchanging personal remarks with a professor or displaying a confident “at-homeness” in the lounge and the library. I was an outsider at first, and later as an insider I was still conscious of this status difference among the students.

I did editorial work for Richard Courant, the director, and I studied under his former students Fritz John and Kurt Friedrichs. I knew that Courant, Friedrichs, John, and also Lipman Bers were refugees from Nazi Germany. I even knew that Friedrichs and John had been Courant’s students at Göttingen, a town somewhere in Germany, where the great, preeminent David Hilbert had reigned. But it was only much later, when writing this book, that I really appreciated what that meant. Friedrichs was elected to the National Academy of Sciences and in 1977 received the National Medal of Science, the United States’ highest scientific award. After his retirement, the last talk Courant gave was at Friedrichs’ 70th birthday. He spoke with great feeling about the man he had known for almost half a century as student, colleague, and friend: “He is one of the rare scientists whose intellectual and scientific development has never slackened but has gone forward continually. One of the very wonderful aspects of all this is the fact that even now at the age of seventy years, Friedrichs has not stopped or slackened in his endeavors and the radiant inspiration that emanates from him. . . . he has been and has become steadily more truly a great man of science. What a great human being he is everybody near to him knows very well.”¹⁷

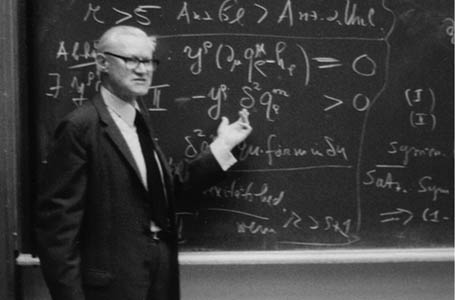
Figure 6-5. Kurt Otto Friedrichs of the Courant Institute. Courtesy of Archives of the Mathematisches Forschungsinstitut Oberwolfach.

Fritz John died in New Rochelle, New York, on February 10, 1994. The following February the Notices of the American Mathematical Society published his obituary, written by Jürgen Moser, who had been both his colleague at NYU and his neighbor in New Rochelle. They often met at the train station in New Rochelle on the way to work at the institute. (Richard Courant and Lipman Bers also were long-time residents of New Rochelle.) During Moser’s first year at NYU, John was working on one of his most important discoveries, the spaces of “bounded mean oscillation.” Moser wrote that for him this discovery of John’s was connected with an unforgettable personal experience. [While they were waiting for the train . . . ] Fritz told Moser about his work on mappings with small strain and explained the subtle estimates for the derivatives it led to. Moser found it very interesting but did not appreciate the depth of this result at that time. But the next morning it just hit him that this inequality provided precisely the tool he needed for overcoming a major difficulty. “Never again,” he wrote, “did I have such luck that a theorem was invented just at the time when I urgently needed it.”

Figure 6-6. Fritz John and Jürgen Moser of the Courant Institute, in conversation. Courtesy of Archives of the Mathematisches Forschungsinstitut Oberwolfach.

The obituary ends with a quote from Courant: “John is one of the most original and deep mathematical analysts of our time . . . completely uncorrupted by the activity of the marketplace, yet a full personality with wide intellectual interest.”¹⁸ Courant had already died in 1972.

Among U.S. math departments today, the Courant Institute of NYU remains special and different. Its faculty’s interests range all the way from pure topics like topology and abstract algebra down to practical applications including meteorology, statistical mechanics, and mathematical physiology. And it still has an inclusive, welcoming attitude toward students and visitors and toward many different viewpoints in pure and applied mathematics. It preserves the Göttingen heritage, the tradition of Klein, Hilbert, and Courant. In response to a book review of the selected works of Peter Lax (my mentor at Courant), I received a message from a reader who had been reminded of his student days at Courant. He wrote that he clearly recalled Lax’s friendly, approachable nature and the very high opinion all his students had of him as a person. He also had some interactions with his wife, Anneli Lax, and found her to be a “kind and gentle human being” too. He recalled how much Professor Friedrichs encouraged students to visit him in his office. The message ended, “He was inspirational. . . . Thanks for triggering my trip down memory lane.”

The Golden Years of Moscow Mathematics

This is the title of a book published by the American Mathematical Society in 1992, edited by Smilka Zdravkovska and Peter L. Duren. It contains 12 articles by Russian mathematicians describing Moscow mathematics from the 1920s to the 1990s. The golden years were from about 1957 to 1968. In the preface, Zdravkovska writes that she was very fortunate to be an undergraduate student at the Mechanics and Mathematics Department (Mekh-Mat) of Moscow State University in the 1960s. It was an exciting environment where you learned as much from fellow students as from the professors. You could pick from among dozens and dozens of courses and seminars offered by first-rate mathematicians, and you also could teach and learn from the bright high school children in the mathematical kruzhoks (circles.) And of course the groups of students bound by close friendships shared other interests outside mathematics.

Vladimir Arnold, one of the most eminent living mathematicians, has written of the constellation of great mathematicians at the Mechanics and Mathematics Department. “It was really exceptional, and I have never seen anything like it at any other place.” Professional mathematicians will recognize the names he lists. “Kolmogorov, Gelfand, Petrovsky, Pontryagin, P. Novikov, Markov, Gelfond, Lusternik, Khinchin, and P. S. Aleksandrov were teaching students like Manin, Sinai, Novikov, V. M. Alexeev, Anosov, A. A. Kirillov, and me. All these mathematicians were so different! It was almost impossible to understand Kolmogorov’s lectures, but they were full of ideas and were really rewarding.”¹⁹ But in 1968 there came a marked chill in the atmosphere, as we will see below.

One of the most interesting contributions to this volume is by A. B. Sossinsky (Alyosha). He was born in Paris in 1937, into a family of Russian émigrés. On his father’s side, he came from Russian nobility that can be traced back to the 16th century; however, the family had lost their land by the turn of the century.

His maternal grandmother, O. E. Kolbasina-Chernova, came from a well-off literary family (her father was a close friend of Ivan Turgenev). She became a Bolshevik, a “professional revolutionary.” Sossinky’s father, on the other hand, fought in the White cavalry against the Bolsheviks, and in World War II for the French Foreign Legion. He then became head of the Russian Verbatim Reports Section at the United Nations and settled in Great Neck, Long Island.

Sossinsky became fascinated with mathematics when the family still lived in France. He was 13 when the French curriculum introduced algebra and geometry. Geometry was his favorite subject, and he began “research” at age 14: “I ‘proved’ that Euclidean geometry is contradictory and ‘showed’ that the Universe is ‘closed’ in the sense that straight lines ‘don’t have two ends’ but are ‘like very big circles.’ I was too shy to communicate my ‘results’ to my teacher (or to other grown-ups) but wrote them up in great detail, in a calligraphic handwriting, and sealed them in an envelope, meant to be opened to the world at large later on, when I would be old enough to be taken seriously.”²⁰

In 1954 he entered Washington Square College of NYU. After a disappointing freshman year, he planned to continue his education in Europe, either in Moscow or in Paris. In the summer of 1955 his family visited Russia. Their 2-month trip was quite a shock. They saw what the standard of living there was truly like and heard first-hand about the tragedy of Stalin’s camps. The family returned to New York, but then in 1957, after another family summer in Moscow, Alyosha decided to stay there. It was a tough decision for him; he knew he could not expect to leave Russia again in the foreseeable future. His parents were neither supportive nor opposed. He did have naïve hopes that Khrushchev would soon be replaced by a younger, better educated, more liberal man, that some form of socialism with a human face would prevail.

During Sossinsky’s undergraduate and postgraduate years (1957–1964), mathematics and mathematicians at Mekh-Mat flourished in a highly stimulating environment. The person most responsible for this was the rector of Moscow University, I. G. Petrovsky, an outstanding mathematician who headed the chair of differential equations for nearly two decades. Petrovsky is remembered even more for his honesty, his personal courage, and his remarkable ability as an administrator. He managed to concentrate a great deal of power in his own hands (“He has more clout than many Central Committee members, although he’s not even in the Party,” a well-informed administrator once told Sossinsky) and used it to expand and enrich the university in general, but especially the Mechanics and Mathematics Department, the apple of his eye.

The graduate math program was headed by the distinguished topologist P. S. Aleksandrov, who was always fond of and helpful to talented math students. With the powerful help of I. G. Petrovsky, he was often successful in continuous struggles with party bosses and the rank and file, especially when N. V. Efimov became the Mekh-Mat dean (1959–1969). In fact, Efimov did most of the infighting with the Party people in his friendly lowkey style. He was an able administrator, a very popular and careful man.

Figure 6-7. I. G. Petrovsky, rector of Moscow University and leading researcher in partial differential equations. Courtesy of the Independent University of Moscow and Moscow Center for Continuous Mathematical Education.

Sossinsky adds the name of Andrei Kolmogorov, who held no administrative position but was one of the world’s outstanding mathematical thinkers. “He symbolized the total scientific involvement, the intellectual probity viewed by many of us as the ideal for a mathematician.” Sossinsky writes:

It must be difficult for Western mathematicians to understand how, in a totalitarian society, scientific achievement as the main criterion for success in scientific institutions is something absolutely unusual. The usual criterion at the time in Russia was politics or ideology, not scientific truth. . . . Mekh-Mat, until the end of 1968, was a unique place, an oasis, a haven where the objective value of one’s research work was one’s best asset. This was understood and accepted by most students and teachers; it was an essential feature of the atmosphere at Mekh-Mat at the time. Our love of mathematics was, for most of us, part of a common outlook, characterized by anti-establishment political views and by a great interest in the artistic and literary life of the times and in active sports (especially mountain hiking, camping, canoe, cross-country and downhill skiing.)²¹

This use of mathematics as an escape from an oppressive reality is an example of a theme we developed in chapter 3.

In the same book, D. B. Fuchs, who was also a student at Mekh-Mat during its golden years, writes that the Brezhnev era began with several political trials, and the general atmosphere in the country was dreadful. “One of the important features of our political life in the late 1960s was ‘signing letters.’ After the trial of the writers Andrei Sinyavsky and Yuli Daniel, some groups of people wrote collective letters to various power institutions with various kinds of protest (from rather mild to very strong). Of course, the authors of the letters were punished, but the letters kept on being written. . . . In order to stop the campaign, the authorities had to choose one of the letters for an exemplary punishment of its authors. And it seems that they chose the letter about Esenin-Volpin.”²²

Alexander Sergeyevich Esenin-Volpin was the son of the great Russian poet Sergeii Esenin, a good mathematical logician, and a confirmed dissident. In January 1968 he was taken to a psikhushka—a special psychiatric hospital for political deviants.

Figure 6-8. Andrei Kolmogorov (left), great Russian mathematician, with younger colleagues. Courtesy of Archives of the Mathematisches Forschungsinstitut Oberwolfach.

A letter in his defense was signed by 99 mathematicians. . . . The signers began to be pursued. There were meetings at various places where they were vilified by their colleagues. . . . Nobody knew what might happen. And we did a wise thing. A small group of mathematicians (including Shafarevich, Arnold, Tyurina, myself and some others) went to a remote skiing place in the Caucasus. We had no connection with the outer world and did not want to know what was going on in Moscow. And when we returned everything had been settled. There had been discussions in some high spheres, and it was decided to act without extreme measures. Thank God, nobody was arrested. Two people lost their primary jobs, and some people lost their secondary jobs. Many people had difficulties with promotions. No one was allowed to go abroad.²³

We return to Sossinsky. “The year 1968 [the year of the Essenin-Volpin letter] was the turning point of many lives, including my own. It was the year of the May barricades in Paris, of draft-card burning and riots on American campuses, of the Prague spring crushed by Russian tanks. For me it was the year that put an end to my hopes and illusions, the year of dramatic events that marked the end of the Mekh-Mat golden era.”

The letter was almost immediately published in the West, against the wishes of its authors and cosigners. The letter was the pretext for a crackdown at the Moscow University math department: the administration at Mekh-Mat and the party leaders were all subsequently replaced by hard-liners. Along with this crackdown came the organization of systematic anti-Semitic practices at the Mekh-Mat examinations.

Sossinsky remembers a boy named Kogan (a Russian version of Cohen) who was taking the entrance exam for the second time. He scored 5 (the maximum) on written math, 5 on oral math (surviving 4 hours of olympiad-level questions), and 5 on oral physics (where the two examiners were also out to get him.) That left the Russian literature essay, where even a passing grade would get him in. There were no spelling, grammar or stylistic mistakes in his essay, and Kogan had been an A student in literature, but he was given a 2 (= F) for “not clarifying the topic.”

Sossinsky wrote, “I have never seen Kogan since. (Thank God. What would I have said to him?) For the first time I asked myself the question: what moral right did I have, as teacher, to be, if not an accomplice to, then a passive observer of, such practices?”²⁴

In 1971 the Mekh-Mat party bureau decided to forbid Sossinsky to teach at School No. 12. In 1974 he wrote his resignation from the department. Then the chairman, P. S. Aleksandrov, invited him to his apartment to discuss the situation. Aleksandrov began with the following remarkable opening gambit: “Alyosha, traditionally we intellectuals of the Russian nobility have always placed our duty to the fatherland above our personal interests and feelings. A Russian nobleman does not leave a sinking ship—he fights to keep it afloat. It is people like Kolmogorov, like you and me, who have made this department into the unique scientific oasis that you know. Even in the Stalin years, we have always done all we could, swallowing our pride if need be . . . .”²⁵

Sossinsky had known that Aleksandrov’s parents were small-landed gentry, but he had expected anything but an appeal to values that 50 years of Bolshevik rule were supposed to have eradicated, especially in a careful and successful establishment scientist.

Sossinsky provides a psychological interpretation of how members of these outstanding institutions coped with these political pressures. He analyzed how the Mekh-Mat he knew and loved had been destroyed “by humiliating a student or a professor, forcing him to dig potatoes out of the mud by hand (as “voluntary” help for a local collective farm), making him hypocritically repeat, in public, obvious political lies about the system, the system succeeds in making this person lose his sense of self-respect. Then he becomes manageable.”²⁶

Talented people, who tend to be unpredictable and more difficult to control, are flunked at the entrance exams, or not recommended for graduate work, or not given positions in the department, unless their sense of self-respect is broken and they can prove their docility. “What the hard-line administrators wanted were good, competent, solid, stolid, servile mathematicians. And that’s what they now have. There are very few world-class mathematicians holding a full-time position at Mekh-Mat today [1991], while there were dozens and dozens in 1968.”²⁷

The Jewish People’s University

There is a little-known postscript to this story of Moscow mathematics. In 1978, a few years before the publication of the book The Golden Years of Moscow Mathematics, from which we have been quoting, a spontaneous, half-underground school of math called the Jewish People’s University was created and served those excluded from Mekh-Mat. Bella Abramovna Subbotovskaya was a Jewish woman mathematician who in the mid-1950s had been a Mekh-Mat student. Now she organized classes covering the material taught to beginning students at Mekh-Mat—complex analysis, real analysis, topology, and algebra. With the help of her friends Valery Senderov (a well-known dissident) and Boris Kanevsky, she recruited first-class lecturers such as Dmitry Fuchs and Victor Ginzburg. She had a policy strictly forbidding any politics. Mathematics was taught, by volunteers, outside the official Soviet school system—that was all. About 350 students attended the school from 1978 to 1983. In March 1982, the famous U.S. topologist John Milnor taught there while visiting Moscow.

Andrei Zelevinsky, who is now at Northeastern University, writes that Bella Abramovna drew up lists of students, arranged places for class meetings, informed everyone of changes in scheduling, made sure that classes met and adjourned on time, brought chalk, and even made delicious sandwiches. “She accomplished all these tasks with a smile and without obvious efforts. Her mere presence created a wonderfully pleasant, warm, and homely environment. She took care of all practical everyday problems of all the instructors. By the way, it goes without saying that no one received any money for their work.”²⁸

Of course, such a thing could not go on without attracting the attention of the KGB. In 1982 Subbotovskaya was called in for questioning. It is believed that she refused to cooperate in testifying against Kanevsky or Senderov. Then a strange thing happened. At about eleven o’clock, on the night of September 23, 1982, as Bella was walking home down a quiet street after visiting her mother, a truck ran into her at high speed and then drove away. A few minutes later an automobile stopped nearby, and soon after that an ambulance appeared and took her dead body to the morgue. The funeral service was attended by a few friends and family members. No one dared to voice their suspicions. Kanevsky and Senderov were imprisoned, for 3 and 5 years, respectively. The Jewish People’s University ceased to exist.

Figure 6-9. Bella Abramovna Subbotovskaya. Courtesy of Ilya Muchnik.

Association for Women in Mathematics

Women mathematicians have faced different challenges. They confront centuries-old discrimination based on their gender. The founding of the Association for Women in Mathematics (AWM) was motivated by women’s determination to be accepted as equals in mathematical circles and by the difficulty they have had in obtaining good academic jobs. At the 1971 Joint Mathematics Meetings women activists called for a caucus. They were aware of the very discouraging statistics about their status in their field as reflected by the scarcity of women in the program. None of the invited, hour-long speakers were women, and only 5 percent of the short talks were given by females. A similar gender disparity existed in academic jobs; only 1 of 10 promotions listed that year in Notices of the American Mathematical Society was given to a woman. At the instructors’ level they were better represented: 33 percent of the jobs listed were held by women. The American Mathematical Society (AMS) was run by men, with no major elected positions held by their female peers.

Soon after the caucus was established, the organizers transformed it into an independent organization called the Association for Women in Mathematics. Mary Gray, a professor at the American University, was instrumental in its formation and became its first president. As part of her leadership, she wrote the first issue of the organization’s newsletter, a publication that provides the vital link that builds this community to this day.

For Lenore Blum, a difficult early experience at Berkeley transformed her “from being naive about the politics for women in academia, to taking an active part in helping women navigate the difficult terrain of such a traditionally male field as mathematics.”²⁹ It was at that time that Blum became active in local and national organizations, and she formed strong ties with other women in science, including Judy Roitman. She served from 1975 to 1978 as the third president of the Association for Women in Mathematics. Her search for a supportive community led her to combine political activism and mathematical research. She believed that rather than adjusting to existing established organizations, one needed to create new ones.

The AWM’s members’ activities are wide-ranging: they document the status of women in mathematics; they influence public policy and that of granting agencies; their speakers’ bureau maintains close connections with high schools and colleges; and they address the many forms of bias held against women interested in mathematics.

The organization also celebrates the lives and contributions of women mathematicians (for instance, by a colloquium honoring Emmy Noether) and dedicates prizes and offers scholarships in acknowledgment of their most famous predecessors. AWM’s political and educational impact is impressive for an organization with 4000 members. Government and scientific groups frequently consult its members. The organization also helps develop the mathematical potential of high school and college women through conferences and workshops.

Figure 6-10. Mary Gray (left), founder of the Association for Women in Mathematics, with friends. Courtesy of AWM, AWM Newsletter 23(3), 25.

Many of these kinds of activities are regularly performed by effective professional organizations in science. But AWM goes beyond these usual contributions; it is a community of practice and shared beliefs, which is emotionally significant in the lives of its members. Jean E. Taylor and Sylvia Wiegand described AWM as a “passionate organization.” The readers of the bimonthly newsletter comment that “each issue ‘recharges’ them and helps them fight feelings of isolation.” The persistence of discrimination contributes to these feelings. In a special issue of Notices it was reported that while female enrollment in advanced math classes has increased since the establishment of AWM, increase in tenured appointments at prestigious universities is still proceeding slowly.³⁰

It is not surprising that this discrimination has psychological consequences. In the same issue of Notices, D. J. Lewis writes that there are clear indications that at every level, from middle school to doctoral programs, women generally are less confident in their mathematical abilities than men. Successful women do receive encouragement and assurance of their abilities from parents and instructors, yet for many successful women in mathematics, there is always a doubt that they are as good as they are. “Perhaps, some of this self-doubt arises because the general public has come to view mathematics as masculine and early on women perceive themselves as outsiders to the mathematical world.”³¹

Figure 6-11. Lenore Blum (far right) and colleagues. Courtesy of the American Mathematical Society.

Many women still feel isolated and embattled in their roles as mathematicians. Not only do they need to prove that they are effective in their chosen profession, and prove it again and again, they also need to show that they have not abandoned their sense of identity as women. At AWM meetings, in their publications, and through their friendships with other members, they are able to discuss these dilemmas. They share their concerns about “the two-body problem”—that is, the professional challenge, when married to a male mathematician, of trying to find jobs together.

In biographies, personal accounts, and presentations of male mathematicians, reference to their personal lives is limited. This is not the case in writings by and about women. Throughout the book Complexities, written by members of the AWM, emotional conflicts and issues are freely and frequently discussed. At the same time, the volume includes technically demanding papers in mathematics, and facts and figures about the slowly changing status of women in the profession. In this way, the contributors overcome the usual dichotomy between intellect and emotion.

Women mathematicians are subject to discouraging cultural messages. One is the belief that they lack an aptitude for mathematics. Another is the argument that math lacks the intuitive sensibility so important to women who cherish relationships. In confronting these opinions, women in the AWM have asserted that mathematics provides them with a rewarding profession, a way to use their intellect maximally, without jeopardizing a full emotional life and broad humanistic interests.

Other contributors to Complexities write of the impact of math and computer camps for high school students, of special women’s mentoring programs at prestigious institutions, and of networking and support groups including the AWM. The difference that such activities have made in the lives of women aspiring to be mathematicians is made clear by Judy Roitman when she recalls the past: “It was not uncommon for major women mathematicians to be unemployed; young women were routinely discouraged; the few who persevered were usually treated badly; and role models were few and far between.”³²

There have been important changes throughout the 20th century regarding women’s access to mathematical careers. The most important of these is a change in university policies. At the beginning of the century, women in many countries could not take classes for official credit. They could only audit classes, and only with permission of the lecturer. And even when they were allowed to audit, women often were not ready for the university courses because of the inferior education they had received earlier.

Many universities continued to discourage women applicants in the decades before World War II. Even after such policies became illegal, attitudes toward women interested in mathematics remained prejudicial. The ensuing psychological injury has healed slowly. The sense of inadequacy, from which many women continue to suffer, manifests itself in a more fragile self-concept. The studies of Benbow and Stanley further contributed to societal stereotypes. But since then, meta-analyses of large databases show a steady shrinking of gender differences in mathematical achievement. Most research on the cognitive abilities of males and females, from birth to maturity, does not support the claim that men have greater intrinsic aptitude for mathematics and science. These findings do not receive the publicity that greeted earlier studies focusing on gender differences. But they contribute to make equity a reality, through intervention programs for women and minorities. Most important are the encouragement provided by caring mentors and the group interaction of students drawn from previously marginalized groups.

At the beginning of this chapter we asked, What kinds of communities do mathematicians form? The range of groups in which mathematicians function professionally is very broad. There are some communities that enrich their members’ lives in very significant ways. Whether within institutions or formed intentionally outside traditional universities, they provide meaningful connections for their members. Some have a clear, shared vision. Others provide enthusiasm and cooperation. Their existence and importance refute the myth of the solitary, isolated nature of mathematical life.

Bibliography

Abelson, P. (1965). Relation of group activity to creativity in science. Daedalus (summer), p. 607.

Albers, D. J., & Alexanderson, G. L. (Eds.) (1985). Mathematical people: Profiles and interviews. Boston: Birkhäuser.

Aleksandrov, P. S. (2000). “A few words on A. N. Kolmogorov,” in Kolmogorov in Perspective. Providence, R.I.: American Mathematical Society, pp. 141–144.

Beaulieu, L. (1993). A Parisian café and ten proto-Bourbaki meetings (1934–1935). Mathematical Intelligencer 15(1), 27–35.

Beaulieu, L. (1999). Bourbaki’s art of memory. Osiris 2, 2nd series, vol. 14, Commemorative Practices in Science: Historical Perspectives on the Politics of Collective Memory, pp. 219–251.

Bell, E. T. (1937). Men of mathematics. New York: Simon & Schuster.

Birman, J. (1991). In her own words. Notices of the American Mathematical Society 38(7), 702.

Blum, L. (2005). AWM’s first twenty years: The presidents’ perspectives. In B. A. Case & A. M. Leggett (Eds.). Complexities: Women in mathematics. Princeton N.J.: Princeton University Press, pp. 80–97.

Bourbaki, N. (1948). Foundations of mathematics for the working mathematician. Journal of Symbolic Logic 14, 1–14.

Bourbaki, N. (1950). The architecture of mathematics. American Mathematical Monthly 57, 221–232.

Brown-Walker, J. (2005). A double dose of discrimination. In B. A. Case & A. M. Leggett (Eds.). Complexities: Women in mathematics. Princeton, N.J.: Princeton University Press, pp. 189–190.

Cartan, H. M. (1980). Nicolas Bourbaki and contemporary mathematics. Mathematical Intelligencer 2(4), 175–187.

Case, B. A., & Leggett, A. M. (Eds.) (2005). Complexities: Women in mathematics. Princeton, N.J.: Princeton University Press.

Courant, R. (1980). Reminiscences from Hilbert’s Göttingen. Mathematical Intelligencer, 3(3), 154–164.

Dieudonné, J. A. (1970). The work of Nicholas Bourbaki. American Mathematical Monthly 77, 134–145.

Fleck, L. (1979). Genesis and development of a scientific fact. Chicago: University of Chicago Press.

Fuchs, D. B. (1993). On Soviet mathematics of the 1950s and 1960s. In S. Zdravkovska & P. L. Duren (Eds.). Golden years of Moscow mathematics, History of Mathematics, vol. 6. Providence, R.I.: American Mathematical Society, 220–222.

Gowers, T., & Nielsen, M. (2009). Massively collaborative mathematics. Nature 461, 879–881.

Grothendieck, A. (1986). Récoltes et Semailles. Unpublished manuscript.

Guedj, D. (1985). Nicholas Bourbaki, the collective mathematician: An interview with Claude Chevalley. Mathematical Intelligencer 7(2), 18–22.

Heims, S. J. (1980). John von Neumann and Norbert Wiener: From mathematics to the technologies of life and death. Cambridge, Mass.: MIT Press.

Helson, R. (2005). Personal communication.

Henrion, C. (1997). Women in mathematics. Bloomington, Ind.: Indiana University Press.

Hersh, R., & John-Steiner, V. (1993). A visit to Hungarian mathematics. Mathematical Intelligencer 15(2), 13–26.

Honda, K. (1975). Teiji Takagi: A biography. Commentary. Mathematica Universitatis Sancti Pauli XXIV-2, 141–167.

John, F. (1992). Memories of student days in Göttingen. Miscellanea Mathematica. New York: Springer, pp. 213–220.

Klein, F. (1979). Development of mathematics in the 19th century. Translated by M. Ackerman. In R. Hermann. Lie groups, history, frontiers and applications, vol. IX. Brookline, Mass.: Math Science Press.

Kline, M. (1974). Why Johnny can’t add. New York: Random House.

Lewis, D.J. (1991). Mathematics and women: The undergraduate school and pipeline. Notices of the American Mathematical Society 38(7), 721–723.

Lui, S. H. (1997). An Interview with Vladimir Arnol’d. Notices of the American Mathematical Society 42(2), 432–438.

MacTutor web Site. Mathematical biographies: Élie Joseph Cartan, Henri Paul Cartan, Pierre Émile Jean Cartier, Claude Chevalley, Jean Alexandre Eugene Dieudonné.

Mashaal, M. (2006). Bourbaki: A secret society of mathematicians. Providence, R.I.: American Mathematical Society.

Mathias, A. R. D. (1992). The ignorance of Bourbaki. Mathematical Intelligencer 14(3), 4–13.

Moser, J. (1995). Obituary for Fritz John, 1910–1994. Notices of the American Mathematical Society 42(2), 256–257.

Pier, J. P. (Ed.) (2000). Development of mathematics 1950–2000. Boston: Birkhäuser.

Reid, C. (1983). K. O. Friedrichs 1901–1982. Mathematical Intelligencer 5(3), 23–30.

Reid, C. (1992). Hilbert. New York: Springer-Verlag.

Reid, C. (1996). Julia: A life in mathematics. Washington, D.C.: MAA Spectrum.

Roberts, S. (2006). King of infinite space. New York: Walker and Company.

Roitman, J. (2005). In B. A. Case and A. M. Leggett (Eds.). Complexities: Women in mathematics. Princeton N.J.: Princeton University Press, p. 251.

Rota, G. C. (1987). The lost café. Los Alamos Science, Special Issue, p. 26.

Rowe, D. E. (1986). “Jewish Mathematics” at Göttingen in the era of Felix Klein. Isis 77, 422–449.

Rowe, D. E. (1989). Klein, Hilbert, and the Göttingen mathematical tradition. In K. M. Oleska (Ed.). Science in Germany: The intersection of institutional and intellectual issues. Osiris 5, 189–213.

Rowe, D. E. (2000). Episodes in the Berlin-Göttingen rivalry, 1870–1930. Mathematical Intelligencer 22(1), 60–69.

Schechter, B. (1998). My brain is open: The mathematical journeys of Paul Erdős. New York: Simon and Schuster.

Segal. S. L. (2003). Mathematicians under the Nazis. Princeton, N.J.: Princeton University Press.

Senechal, M. (1998). The continuing silence of Bourbaki—An interview with Pierre Cartier, June 18, 1997. Mathematical Intelligencer 20(1), 22–28.

Shifman, M. (Ed.) (2005). You failed your math test, Comrade Einstein. Singapore: World Scientific.

Socha, K. (2005). Mathematics: Mortals and morals. In B. A. Case & A. M. Leggett (Eds.). Complexities: Women in mathematics. Princeton N.J.: Princeton University Press, pp. 393–395.

Sossinsky, A. B. (1993). In the other direction. In S. Zdravkovska & P. L. Duren (Eds.). Golden years of Moscow mathematics, History of mathematics, vol. 6. Providence, R.I.: American Mathematical Society, pp. 223–243.

Szanton, A. (1992). The recollections of Eugene P. Wigner as told to Andrew Szanton. New York: Plenum Press.

Szpiro, G. G. (2007). Bella Abramovna Subbotovskaya and the “Jewish People’s University.” Notices of the American Mathematical Society 54(10), 1326–1330.

Tikhomirov, V. M. (1991). Moscow mathematics 1950–1975. Basel: Birkhäuser.

The Scientist (1992). Academy criticism of a foreign associate stirs debate over NAS role and policies. 6(19), 1–18.

Ulam, S. (1976). Adventures of a mathematician. New York: Scribner.

van der Waerden, B. L. (1937). Moderne algebra. Berlin: Springer.

Weil, A. (1992). The apprenticeship of a mathematician. Basel: Birkhäuser.

Zelevinsky, A. (2005). Remembering Bella Abramovna. In M. Shifman (Ed.). You failed your math test, Comrade Einstein. Singapore: World Scientific.

Zdravkovska, S., & Duren, P. L. (Eds.) (1993). Golden years of Moscow mathematics, History of mathematics, vol. 6. Providence, R.I.: American Mathematical Society.