The SAS programs used in the text are provided in this section, which are also posted at the companion website for easy downloading. It should be noted that although the SAS programs below are all for the normal distribution, the call randgen function can be adjusted to generate observations from any desired distribution.
The following table lists the figures containing SAS output.
| Figure number |
Figure title |
SAS program number |
| 4.2 |
SAS output of the RL distribution where the design parameters (n = 10, a = 10) of the Shewhart‐SN chart were chosen for a nominal ARLIC = 500 |
1 |
| 4.4 |
SAS output of the RL distribution where the design parameters (n = 13, a = 81) of the Shewhart‐SN chart were chosen for a nominal ARLIC = 500 |
2 |
| 4.5 |
SAS output of the RL distribution where the design parameters (n = 10, k = 6, h = 4) of the CUSUM‐SN chart were chosen for a nominal ARLIC = 500 |
3 |
| 4.6 |
SAS output of the RL distribution where the design parameters (n = 10, k = 41, h = 24) of the CUSUM‐SR chart were chosen so that nominal ARLIC = 500 |
4 |
| Figure number |
Figure title |
SAS program number |
| 4.7 |
SAS output of the RL distribution where the design parameters (n = 1, λ = 0.10, L = 2.667) of the EWMA‐SN chart were chosen for a nominal ARLIC = 500 |
5 |
| 4.8 |
SAS output of the RL distribution where the design parameters (n = 10, λ = 0.1, L = 2.794) of the EWMA‐SR chart were chosen for a nominal ARLIC = 500 |
6 |
| 4.23 |
SAS output of the RL distribution where the design parameters (m = 1000, n = 5, j = 3, a = 48, b = 953) of the Shewhart‐Prec chart were for a nominal ARLIC = 500 |
7 |
| 4.24 |
SAS output where the design parameters (m = 500, n = 5, 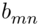 = 2172) of the Shewhart‐MW chart were chosen for a nominal ARLIC = 500 |
8 |
| 4.25 |
SAS output where the design parameters (m = 125, n = 5, j = 3, h = 9.775, k = n(d*‐d)) of the CUSUM‐EX chart were chosen for a nominal ARLIC = 500 |
9 |
| 4.26 |
SAS output where the design parameters (m = 100, n = 5, h = 353, k = 0) of the CUSUM‐Rank chart were chosen for a nominal ARLIC = 500 |
10 |
| 4.27 |
SAS output where the design parameters (m = 100, n = 5, λ = 0.10, L = 2.220) of the EWMA‐EX chart were chosen for a nominal ARLIC = 500 |
11 |
| 4.28 |
SAS output where the design parameters (m = 100, n = 5, λ = 0.10, LCL = 219.5, UCL = 310.5) of the EWMA‐Rank chart were chosen for a nominal ARLIC = 500 |
12 |
| SAS program number |
Figure title |
Figure number |
| 1 |
SAS output of the RL distribution where the design parameters (n = 10, a = 10) of the Shewhart‐SN chart were chosen for a nominal ARLIC = 500 |
4.2 |
| SAS program |
|
For the Shewhart‐SN chart, the SAS program for the EWMA‐SN chart (SAS program number 5 shown below) can be used with λ = 1. |
| SAS program number |
Figure title |
Figure number |
| 2 |
SAS output of the RL distribution where the design parameters (n = 13, a = 81) of the Shewhart‐SN chart were chosen for a nominal ARLIC = 500 |
4.4 |
| SAS program |
| For the Shewhart‐SR chart, the SAS program for the EWMA‐SR chart (SAS program number 6 shown below) can be used with λ = 1 |
| SAS program number |
Figure title |
Figure number |
| 3 |
SAS output of the RL distribution where the design parameters (n = 10, k = 6, h = 4) of the CUSUM‐SN chart were chosen for a nominal ARLIC = 500 |
4.5 |
| SAS program |
proc iml;
* Number of simulations;
sim = 10000;
* Design parameters of CUSUM control chart;
n = 10;
H = 4;
k = 6;
* Size of the shift;
shift = 0;
*One-sided or two-sided chart;
*If one-sided, then type = 1;
*If two-sided, then type = 2;
type = 2;
*Constructing the control chart;
runl = j(sim,1,.);
stdev = 1;
xi = j(n,1,.);
ti_vec = j(n,1,.);
|
do o = 1 to sim;
* Initializing values;
indicator = 0;
count = 0;
Ci_1_plus = 0;
Ci_1_minus = 0;
do i = 1 to 1000000000000000 until (indicator = 1);
count = count + 1;
* Generating observations from the Normal distribution;
call randgen(xi,‘NORMAL’,shift,1);
do u = 1 to nrow(xi);
if xi[u,]>=0 then ti_vec[u,]=1;
else ti_vec[u,]=0;
end;
ti = ti_vec[+,];
sni=2*ti - n;
* Charting statistics;
Ci_plus = max(0, (Ci_1_plus + sni - k));
Ci_minus = max(0, (Ci_1_minus - sni - k));
*Comparing the charting statistics to the control limits;
if type = 2 then do;
if ((Ci_plus >= H) | (Ci_minus >= H)) then indicator = 1;
end;
if type = 1 then do;
if Ci_plus >= H then indicator = 1;
end;
Ci_1_plus = Ci_plus;
Ci_1_minus = Ci_minus;
end;
runl[o,1] = count;
end;
create CUSUM from runl[colname={RL}];
append from runl;
proc univariate data = CUSUM noprint;
histogram;
inset mean std p5 q1 median q3 p95 / format=10.2 pos = ne;
run;
|
| SAS program number |
Figure title |
Figure number |
| 4 |
SAS output of the RL distribution where the design parameters (n = 10, k = 41, h = 24) of the CUSUM-SR chart were chosen so that nominal ARLIC = 500 |
4.6 |
| SAS program |
|
The SAS program for the CUSUM-SR is similar to that of the CUSUM-SN chart above, except that the one line of coding, namely |
sni = 2*ti - n; |
should be altered to compute the  statistic instead of the  which can easily be done making use of the RANKTIE function of SAS. This SAS program is not given here, for brevity. Instead, the SAS program for the Markov chain approach is given below so that the interested reader can see the programming complexities of the programming the Markov chain approach in SAS as opposed to making use of simulation. |
proc iml;
* The reference value;
k = 41;
* The decision interval;
h = 24;
* The sample size;
n = 10;
* The z-value will be used in the calculation of the pmf, P(N = z), and the cdf, P(N< = z);
z = 1000000;
|
* The following values will be used to calculate the 5th, 25th, 50th, 75th and 95th percentiles, respectively;
p5p = 0.05;
p25p = 0.25;
p50p = 0.5;
p75p = 0.75;
p95p = 0.95;
* Calculating the state space;
SRn = do((-n*(n+1)/2),(n*(n+1)/2),2)`;
S = j(nrow(SRn),1,1);
do i = 1 to nrow(SRn);
S[i,] = min(h,(max(0,SRn[i,]-k)));
end;
do i = 1 to nrow(S);
do j = 1 to nrow(S);
if i = j then S[i,] = S[i,];
else if S[i,] = S[j,] then S[j,] = 999;
end;
end;
S = S[loc(S<999)];
upper_limit = (n*(n+1))/2 - k;
if h > upper_limit then print "Not possible";
S_S = j(nrow(S),1,0);
do i = 1 to nrow(S);
S_S[i,] = -S[i,];
end;
S = S||S_S;
SS = j(nrow(S)+nrow(S),1,0);
do i = 1 to nrow(SS) by 2;
SS[i,] = S[(i+1)/2,1];
SS[i+1,] = S[(i+1)/2,2];
end;
SS = SS[2:nrow(SS),]; |
* Defining the vector eta used in the formula for the ARL given by E(N) = eta*inv(I-Q)*one;
eta = j(1,nrow(SS)-2,1);
do i = 1 to nrow(SS)-1;
if i = 1 then eta[1,i] = 1;
else eta[1,i] = 0;
end;
* Calculating the transition probability matrix;
P = j( nrow(SS) , nrow(SS), 0);
* Wilcoxon signed-rank probabilities for a sample size of 4;
if n = 4 then do;
T4 = j((n*(n+1)/2)+1,1,1);
T4[1:3,] = 1;
T4[4:8,] = 2;
T4[9:11,] = 1;
T = T4/(2**n);
end;
* Wilcoxon signed-rank probabilities for a sample size of 5;
if n = 5 then do;
T5 = j((n*(n+1)/2)+1,1,1);
T5[1:3,] = 1;
T5[4:5,] = 2;
T5[6:11,] = 3;
T5[12:13,] = 2;
T5[14:16,] = 1;
T = T5/(2**n);
end;
* Wilcoxon signed-rank probabilities for a sample size of 6;
if n = 6 then do;
T6 = j((n*(n+1)/2)+1,1,1);
T6[1:3,] = 1;
T6[4:5,] = 2;
T6[6,] = 3;
T6[7:9,] = 4;
T6[10:13,] = 5;
T6[14:16,] = 4;
T6[17,] = 3;
T6[18:19,] = 2;
T6[20:22,] = 1;
T = T6/(2**n);
end;
|
* Wilcoxon signed-rank probabilities for a sample size of 7;
if n = 7 then do;
T7 = j((n*(n+1)/2)+1,1,1);
T7[1:3,] = 1;
T7[4:5,] = 2;
T7[6,] = 3;
T7[7,] = 4;
T7[8:9,] = 5;
T7[10,] = 6;
T7[11:12,] = 7;
T7[13:17,] = 8;
T7[18:19,] = 7;
T7[20,] = 6;
T7[21:22,] = 5;
T7[23,] = 4;
T7[24,] = 3;
T7[25:26,] = 2;
T7[27:29,] = 1;
T = T7/(2**n);
end;
* Wilcoxon signed-rank probabilities for a sample size of 8;
if n = 8 then do;
T8 = j((n*(n+1)/2)+1,1,1);
T8[1:3,] = 1;
T8[4:5,] = 2;
T8[6,] = 3;
T8[7,] = 4;
T8[8,] = 5;
T8[9,] = 6;
T8[10,] = 7;
T8[11,] = 8;
T8[12,] = 9;
T8[13,] = 10;
T8[14,] = 11;
T8[15,] = 12;
T8[16:18,] = 13;
T8[19,] = 14;
T8[20:22,] = 13;
T8[23,] = 12;
T8[24,] = 11;
T8[25,] = 10;
T8[26,] = 9;
T8[27,] = 8;
T8[28,] = 7;
T8[29,] = 6;
T8[30,] = 5;
T8[31,] = 4;
T8[32,] = 3;
T8[33:34,] = 2;
T8[35:37,] = 1;
T = T8/(2**n);
end; |
* Wilcoxon signed-rank probabilities for a sample size of 9;
if n = 9 then do;
T9 = j((n*(n+1)/2)+1,1,1);
T9[1:3,] = 1;
T9[4:5,] = 2;
T9[6,] = 3;
T9[7,] = 4;
T9[8,] = 5;
T9[9,] = 6;
T9[10,] = 8;
T9[11,] = 9;
T9[12,] = 10;
T9[13,] = 12;
T9[14,] = 13;
T9[15,] = 15;
T9[16,] = 17;
T9[17,] = 18;
T9[18,] = 19;
T9[19:20,] = 21;
T9[21,] = 22;
T9[22:25,] = 23;
T9[26,] = 22;
T9[27:28,] = 21;
T9[29,] = 19;
T9[30,] = 18;
T9[31,] = 17;
T9[32,] = 15;
T9[33,] = 13;
T9[34,] = 12;
T9[35,] = 10;
T9[36,] = 9;
T9[37,] = 8;
T9[38,] = 6;
T9[39,] = 5;
T9[40,] = 4;
T9[41,] = 3;
T9[42:43,] = 2;
T9[44:46,] = 1;
T = T9/(2**n);
end;
* Wilcoxon signed-rank probabilities for a sample size of 10;
if n = 10 then do;
T10 = j((n*(n+1)/2)+1,1,1);
T10[1:3,] = 1;
T10[4:5,] = 2;
T10[6,] = 3;
T10[7,] = 4; |
T10[8,] = 5;
T10[9,] = 6;
T10[10,] = 8;
T10[11,] = 10;
T10[12,] = 11;
T10[13,] = 13;
T10[14,] = 15;
T10[15,] = 17;
T10[16,] = 20;
T10[17,] = 22;
T10[18,] = 24;
T10[19,] = 27;
T10[20,] = 29;
T10[21,] = 31;
T10[22,] = 33;
T10[23,] = 35;
T10[24,] = 36;
T10[25,] = 38;
T10[26:27,] = 39;
T10[28:29,] = 40;
T10[30:31,] = 39;
T10[32,] = 38;
T10[33,] = 36;
T10[34,] = 35;
T10[35,] = 33;
T10[36,] = 31;
T10[37,] = 29;
T10[38,] = 27;
T10[39,] = 24;
T10[40,] = 22;
T10[41,] = 20;
T10[42,] = 17;
T10[43,] = 15;
T10[44,] = 13;
T10[45,] = 11;
T10[46,] = 10;
T10[47,] = 8;
T10[48,] = 6;
T10[49,] = 5;
T10[50,] = 4;
T10[51,] = 3;
T10[52:53,] = 2;
T10[54:56,] = 1;
T = T10/(2**n);
end;
nn = n*(n+1)/2;
|
* Calculating the first column of the transition matrix;
do i = 1 to nrow(SS)-2;
if SS[i,]<0 then uppersmall_t = (k-0+nn)/2;
else if SS[i,] > = 0 then uppersmall_t = (k-SS[i,]+nn)/2;
if SS[i,]> = 0 then lowersmall_t = (-k-0+nn)/2;
else if SS[i,] < 0 then lowersmall_t = (-k-SS[i,]+nn)/2;
if lowersmall_t < = uppersmall_t then P[i,1] = sum(T[(lowersmall_t+1):(uppersmall_t+1),]);
else if lowersmall_t > uppersmall_t then P[i,1] = 0;
end;
* Calculating the middle columns of the transition matrix;
do j = 2 to nrow(SS)-2;
do i = 1 to nrow(SS)-2;
if SS[j,]>0 then if SS[i,]<0 then small_t = ceil((SS[j,]+k-0+nn) / 2);
else if SS[i,]> = 0 then small_t = ceil((SS[j,]+k-SS[i,]+nn) / 2);
if SS[j,]<0 then if SS[i,]>0 then small_t = ceil((SS[j,]-k-0+nn) / 2);
else if SS[i,]< = 0 then small_t = ceil((SS[j,]-k-SS[i,]+nn) / 2);
P[i,j] = T[small_t+1,];
end;
end;
* Calculating the second last column of the transition matrix;
do i = 1 to nrow(SS)-2;
if SS[i,]0 then small_t = ceil((SS[ncol(P)-1,]+k-0+nn) / 2);
else if SS[i,]> = 0 then small_t = ceil((SS[ncol(P)-1,]+k-SS[i,]+nn) / 2);
P[i,ncol(P)-1] = sum(T[small_t+1:nrow(T),]);
end;
* Calculating the last column of the transition matrix;
do i = 1 to nrow(SS)-2;
if SS[i,]>0 then small_t = ceil((SS[ncol(P),]-k-0+nn) / 2);
else if SS[i,]< = 0 then small_t = ceil((SS[ncol(P),]-k-SS[i,]+nn) / 2);
P[i,ncol(P)] = sum(T[1:(small_t+1),]);
end;
P[nrow(P)-1,ncol(P)-1] = 1;
P[nrow(P),ncol(P)] = 1;
* Defining the vector one used in the formula for the ARL given by E(N) = eta*inv(I-Q)*one;
one = j(nrow(P)-2,1,1);
|
* Defining the matrix Q used in the formula for the ARL given by E(N) = eta*inv(I-Q)*one;
Q = P[1:nrow(P)-2,1:nrow(P)-2];
* Defining the identity matrix I used in the formula for the ARL given by E(N) = eta*inv(I-Q)*one;
identity = I(nrow(P)-2);
* Calculating the 5th, 25th, 50th, 75th and 95th percentiles;
pmf = j(z,1,1);
cdf = j(z,1,1);
cdf_5th_p = j(z,1,1);
cdf_25th_p = j(z,1,1);
cdf_50th_p = j(z,1,1);
cdf_75th_p = j(z,1,1);
cdf_95th_p = j(z,1,1);
do i = 1 to z;
pmf[i,1] = eta * (Q**(i-1)) * (identity - Q) * one;
cdf[i,1] = sum(pmf[1:i,1]);
end;
index = j(z,1,1);
do i = 2 to z;
index[i,] = index[i-1,]+1;
end;
* Calculating the 5th percentile;
do i = 1 to z;
cdf_5th_p[i,] = cdf[i,];
if cdf_5th_p[i,]> = p5p then cdf_5th_p[i,] = 999;
end;
cdf_5th_p = cdf_5th_p[loc(cdf_5th_p<999)];
if cdf_5th_p[1,] = 999 then percentile_p5p = 1;
else percentile_p5p = nrow(cdf_5th_p)+1;
* Calculating the 25th percentile;
do i = 1 to z;
cdf_25th_p[i,] = cdf[i,];
if cdf_25th_p[i,]> = p25p then cdf_25th_p[i,] = 999;
end;
cdf_25th_p = cdf_25th_p[loc(cdf_25th_p<999)];
if cdf_25th_p[1,] = 999 then percentile_p25p = 1;
else percentile_p25p = nrow(cdf_25th_p)+1;
|
* Calculating the 50th percentile;
do i = 1 to z;
cdf_50th_p[i,] = cdf[i,];
if cdf_50th_p[i,]> = p50p then cdf_50th_p[i,] = 999;
end;
cdf_50th_p = cdf_50th_p[loc(cdf_50th_p<999)];
if cdf_50th_p[1,] = 999 then percentile_p50p = 1;
else percentile_p50p = nrow(cdf_50th_p)+1;
* Calculating the 75th percentile;
do i = 1 to z;
cdf_75th_p[i,] = cdf[i,];
if cdf_75th_p[i,]> = p75p then cdf_75th_p[i,] = 999;
end;
cdf_75th_p = cdf_75th_p[loc(cdf_75th_p999)];
if cdf_75th_p[1,] = 999 then percentile_p<75p = 1;
else percentile_p75p = nrow(cdf_75th_p)+1;
* Calculating the 95th percentile;
do i = 1 to z;
cdf_95th_p[i,] = cdf[i,];
if cdf_95th_p[i,]> = p95p then cdf_95th_p[i,] = 999;
end;
cdf_95th_p = cdf_95th_p[loc(cdf_95th_p<999)];
if cdf_95th_p[1,] = 999 then percentile_p95p = 1;
else percentile_p95p = nrow(cdf_95th_p)+1;
* Calculating the average run length (ARL);
ARL = eta * inv(identity-Q) * one;
* Calculating the second moment;
N2 = eta * (identity + Q) * (inv((identity-Q)**2)) * one;
* Calculating the standard deviation;
SDRL = sqrt (N2 - ((ARL)**2) );
* Printing the output;
print_cdf = index||cdf;
print_pmf = index||pmf;
|
print k [label = 'Reference value'],
h [label = 'Decision interval'],
n [label = 'Sample size'],
SS [label = 'State Space'],
P [label = 'Transition probability matrix' format = .3],
ARL [label = 'ARL' format = .2],
SDRL [label = 'SDRL' format = .2],
percentile_p5p [label = '5th'],
percentile_p25p [label = '25th'],
percentile_p50p [label = '50th'],
percentile_p75p [label = '75th'],
percentile_p95p [label = '95th'];
run; |
| SAS program number |
Figure title |
Figure number |
| 5 |
SAS output of the RL distribution where the design parameters (n = 1, λ = 0.10, L = 2.667) of the EWMA-SN chart were chosen for a nominal ARLIC = 500 |
4.7 |
| SAS program |
proc iml;
* Number of simulations;
sim = 10000;
* Design parameters of EWMA control chart;
lambda = 0.1;
L = 2.667;
* Sample size;
n = 1;
* Size of the shift;
delta = 0;
*Constructing the NPEWMA-SN chart;
stdev = 1;
mean = delta * stdev/sqrt(n);
runlength = j(sim,1,.);
xi = j(n,1,.);
ti_vec = j(n,1,.);
* Steady state control limits for the EWMA chart;
UCL_steady = 0 + L*sqrt(n)*sqrt((lambda/(2-lambda)));
LCL_steady = 0 - L*sqrt(n)*sqrt((lambda/(2-lambda)));
|
do j = 1 to sim;
* Initializing values;
indicator = 0;
count = 0;
zi_1 = 0;
do i = 1 to 1000000000000000 until (indicator = 1);
count = count + 1;
* Generating observations from the Normal distribution;
call randgen(xi,'normal', mean,1);
do o = 1 to nrow(xi);
if xi[o,]>=0 then ti_vec[o,]=1;
else ti_vec[o,]=0;
end;
ti = ti_vec[+,];
sni = 2*ti - n;
* Charting statistic;
zi = lambda*sni + (1 - lambda) * zi_1;
* Comparing the charting statisitc to the steady state control limits;
if (zi>UCL_steady) | (zi<LCL_steady) then do; indicator = 1; end;
zi_1 = zi;
end;
runlength[j,1] = count;
end;
create EWMA from runlength[colname={RL}];
append from runlength;
proc univariate data = EWMA noprint;
histogram;
inset mean std p5 q1 median q3 p95 / format=10.1;
run; |
| SAS program number |
Figure title |
Figure number |
| 6 |
SAS output of the RL distribution where the design parameters (n = 10, λ = 0.1, L = 2.794) of the EWMA-SR chart were chosen for a nominal ARLIC = 500 |
4.8 |
| SAS program |
proc iml;
* Number of simulations;
sim = 100000;
runl = j(sim,1,.); |
* Design parameters of EWMA control chart;
lambda = 0.1;
L = 2.794;
* Sample size;
n = 10;
* Shift;
gamma = 0;
stdev = 1;
mean = gamma * stdev / sqrt(n);
* Steady state control limits;
UCL = L * sqrt( (lambda / (2-lambda) )) * sqrt ( (n*(n+1)*(2*n+1))/6 );
LCL = -UCL;
do k = 1 to sim;
* Initializing values;
indicator = 0;
count = 0;
zi_1 = 0;
do i = 1 to 10000000000 until (indicator = 1);
count = count + 1;
* Generating observations from the Normal distribution;
tv = 0; * Median of the normal distribution;
xi = j(n,1,.);
sign = j(n,1,.);
abs_diff = j(n,1,.);
sri = j(n,1,.);
call randgen (xi, ‘normal’, mean, 1);
do j = 1 to n;
if xi[j,1] > tv then sign[j,1] = 1;
if xi[j,1] < tv then sign[j,1] = -1;
if xi[j,1] = tv then sign[j,1] = 0;
end;
do j = 1 to n;
abs_diff[j,1] = abs(xi[j,1]-tv);
end;
rank_abs_diff = rank(abs_diff);
do j = 1 to n;
sri[j,1] = sign[j,1] # rank_abs_diff[j,1];
end;
signed_rank = sum(sri);
*Charting statistic;
zi = lambda*signed_rank + (1-lambda)*zi_1;
* Comparing the charting statistic to the control limits;
if (zi>UCL) | (zi<LCL) then do; indicator = 1; end;
zi_1 = zi;
end; |
runl[k,1] = count;
end;
create EWMA from runl[colname = {RL}];
append from runl;
proc univariate data = EWMA noprint;
histogram;
inset mean std p5 q1 median q3 p95 / format = 10.1 pos = ne;
run; |
| SAS program number |
Figure title |
Figure number |
| 7 |
SAS output of the RL distribution where the design parameters (m = 1000, n = 5, j = 3, a = 48, b = 953) of the Shewhart-Prec chart were for a nominal ARLIC = 500 |
4.23 |
| SAS program |
proc iml;
*Design parameters of the control chart;
m=1000;
n=5;
a = 48;
b = 953;
*Number of simulations;
sim = 10000;
* Size of shift;
shift = 0.0;
*Constructing the control chart;
rlvec = j(sim,1,.);
j=(n+1)/2;
do k = 1 to sim;
refx = j(m,1,.);
call randgen(refx,'NORMAL',0,1);
call sort (refx,{1});
ucl = refx[b,1];
lcl = refx[a,1];
count = 0;
signal = 0;
count2 = 0;
vec={};
do i = 1 to 1000000000 until (signal=1);
testy = j(n,1,.); |
call randgen (testy,'NORMAL',shift,1);
call sort(testy,{1});
plotstat = testy[j,1];
count2 = count2+1;
if ((plotstat >= ucl)|(plotstat <= lcl)) then signal = 1;
else signal = 0;
rlvec[k,1] = count2;
end;
end;
results = rlvec;
create runlength_precedence from results[colname = {d000}];
append from results;
quit;
data runlength_precedence;
set work.runlength_precedence;
proc univariate data = runlength_precedence noprint;
var d000;
histogram;
inset mean std p5 q1 median q3 p95/format = 10.2;
run; |
| SAS program number |
Figure title |
Figure number |
| 8 |
SAS output where the design parameters (m = 500, n = 5,  = 2172) of the Shewhart-MW chart were chosen for a nominal ARLIC = 500 |
4.24 |
| SAS program |
proc iml;
m = 500;
n = 5;
ucl = 2172;
lcl = m*n-ucl;
sim = 100000;
rlvec = j(sim,13,.);
do d = 1 to 4 by 0.25;
shift = 4*d-3;
do k = 1 to sim;
refx = j(m,1,.);
xt = j(m,1,.); |
call randgen(refx,‘normal’,0,1);
mn = m*n;
count2 = 0;
c = j(mn,1,.);
testy = j(n,1,.);
signal = 0;
yt = j(n,1,.);
do t = 1 to 1000000000 until (signal = 1);
count1 = 0;
call randgen (testy,‘NORMAL’,d-1,1);
do i = 1 to m;
do j = 1 to n;
count1 = count1+1;
if refx[i,]<testy[j,] then c[count1,] = 1;
else c[count1,] = 0;
end;
end;
mxy = sum(c);
if mxy > = ucl then signal = 1;
else if mxy < = lcl then signal = 1;
else signal = 0;
count2 = count2+1;
rlvec[k,shift] = count2;
end;
end;
end;
create runlength_prec_normal from rlvec[colname = {d000 d025 d050 d075 d100 d125 d150 d175 d200 d225 d250 d275 d300 }];
append from rlvec;
quit;
data runlength_prec_normal;
set work.runlength_prec_normal;
proc univariate data = runlength_prec_normal;
var d000 d025 d050 d075 d100 d125 d150 d175 d200 d225 d250 d275 d300;
histogram;
inset mean std p5 q1 median q3 p95 / format = 10.2 pos = ne; |
| SAS program number |
Figure title |
Figure number |
| 9 |
SAS output where the design parameters (m = 125, n = 5, j = 3, h = 9.775, k = n(d*‐d)) of the CUSUM-EX chart were chosen for a nominal ARLIC = 500 |
4.25 |
| SAS program |
proc iml;
*Size of the IC Phase I sample;
m = 125;
* Answer = 0 if m is even and 1 if m is odd;
answer = 1;
*Number of simulations;
sim = 100000;
runlength = j(sim,1,.);
* Winsorization;
wind = 1000000000000000000000000;
wz = j(sim,1,0);
*Size of the Phase II sample;
n = 5;
*One‐sided or two‐sided chart;
*If one‐sided, then type = 1;
*If two‐sided, then type = 2;
type = 2;
*Design parameters of CUSUM chart;
d = 0.5;
* For small m;
dstar = 0.5*sqrt( (n*(m+n+1)) / (4*m+8) );
k = n*(dstar - d);
*UCL;
H = 9.775;
*Shift;
delta = 0;
stdev = 1;
mean = delta * (stdev/sqrt(n));
|
*Obtaining the median;
keep = j(2,1,.);
if answer = 1 then r = (m+1)/2;
if answer = 0 then r_1 = (m/2);
if answer = 0 then r_2 = ((m+2)/2);
*Generating an IC Phase I sample;
xi = j(m,1,.);
do j = 1 to sim;
* Generating observations from the Normal distribution;
call randgen(xi,‘NORMAL’,0,1);
* Finding the median;
xi_rank = xi || rank(xi);
do l = 1 to m;
*For median odd;
if answer = 1 then do;
if xi_rank[l,2] = r then median = xi_rank[l,1];
end;
*For median even;
if answer = 0 then do;
if xi_rank[l,2] = r_1 then keep[1,] = xi_rank[l,1];
if xi_rank[l,2] = r_2 then keep[2,] = xi_rank[l,1];
end;
if answer = 0 then median = sum(keep)/2;
end;
*Calculating the CUSUM;
count = 0;
indicator = 0;
Ci_1_plus = 0;
Ci_1_minus = 0;
do i = 1 to 100000000000000000 until (indicator = 1);
count = count + 1;
*Generating a Phase II sample;
yi = j(n,1,.);
*Generating observations from the Normal distribution;
call randgen(yi,‘NORMAL’,mean,1);
*Calculating the precedence statistic;
precedence = j(n,1,0);
do i = 1 to n;
if yi[i,]>median then precedence[i,] = 1;
end;
U = sum(precedence);
|
*Charting statistic;
Ci_plus = max (0, (Ci_1_plus + (U - n*d) - k));
Ci_minus = max (0, (Ci_1_minus - (U - n*d) - k));
*Comparing the charting statistics to the control limits;
if type = 2 then do;
if ((Ci_plus > = H) | (Ci_minus > = H)) then indicator = 1;
end;
if type = 1 then do;
if Ci_plus > = H then indicator = 1;
end;
Ci_1_plus = Ci_plus;
Ci_1_minus = Ci_minus;
if count > wind then count = wind;
end;
runlength[j,1] = count;
if runlength[j,1] = wind then wz[j,1] = 1;
end;
wind_prop = sum(wz)/sim;
print wind_prop;
create CUSUM from runlength [colname = {RL}];
append from runlength;
proc univariate data = CUSUM noprint;
histogram;
inset mean std p5 q1 median q3 p95 / format = 10.1 pos = ne; |
| SAS program number |
Figure title |
Figure number |
| 10 |
SAS output where the design parameters (m = 100, n = 5, h = 353, k = 0) of the CUSUM-rank chart were chosen for a nominal ARLIC = 500 |
4.26 |
| SAS program |
proc iml;
*Size of the IC Phase I sample;
m = 100;
*Number of simulations;
sim = 10000;
|
* Winsorization;
wind = 10000000000000000;
*Size of the Phase II sample;
n = 5;
*Shift;
delta = 0;
*Design parameters of CUSUM chart;
exp_w = (n*(n+m+1))/2;
stdev_w = sqrt ( n*m*(n+m+1)/12);
k = 0.5*stdev_w;
*UCL;
H = 353;
*One‐sided or two‐sided chart;
*If one‐sided, then type = 1;
*If two‐sided, then type = 2;
type = 2;
runl = j(sim,1,.);
wz = j(sim,1,0);
stdev = 1;
mean = delta * (stdev/sqrt(n));
do j = 1 to sim;
* Initializing values;
count = 0;
indicator = 0;
Ci_1_plus = 0;
Ci_1_minus = 0;
xi = j(m,1,.);
zeros = j(m,1,0);
* Generating an IC Phase I sample;
* Generating observations from the Normal distribution;
call randgen(xi,‘NORMAL’,0,1);
xii = zeros||xi;
do i = 1 to 100000000000000000 until (indicator = 1);
count = count + 1;
yi = j(n,1,.);
* Generating a Phase II sample; |
* Generating observations from the Normal distribution;
call randgen(yi,‘NORMAL’,mean,1);
*Obtaining the rank‐sum statistics;
ones = j(n,1,1);
yii = ones||yi;
comb = xii // yii;
rank = ranktie(comb[,2]);
comb_rank = comb || rank;
call sort (comb_rank, {2 3}, {3});
W_vec = comb_rank[,1]#comb_rank[,3];
W = sum(W_vec);
*Charting statistic;
Ci_plus = max (0, Ci_1_plus + W - exp_w - k);
Ci_minus = max (0, Ci_1_minus + exp_w - k - W);
*Comparing the charting statistics to the control limits;
if type = 2 then do;
if ((Ci_plus > = H) | (Ci_minus > = H)) then
indicator = 1;
end;
if type = 1 then do;
if Ci_plus > = H then indicator = 1;
end;
Ci_1_plus = Ci_plus;
Ci_1_minus = Ci_minus;
if count > wind then count = wind;
end;
runl[j,1] = count;
if runl[j,1] = wind then wz[j,1] = 1;
end;
wind_prop = sum(wz)/sim;
print wind_prop;
create CUSUM from runl [colname = {RL}];
append from runl;
proc univariate data = CUSUM;
histogram;
inset mean std p5 q1 median q3 p95 / format = 10.2 pos = ne; |
| SAS program number |
Figure title |
Figure number |
| 11 |
SAS output where the design parameters (m = 100, n = 5, λ = 0.10, L = 2.220) of the EWMA-EX chart were chosen for a nominal ARLIC = 500 |
4.27 |
| SAS program |
proc iml;
*Size of the IC Phase I sample;
m = 100;
*Odd (answer = 1) or Even (answer = 0);
answer = 0;
*Number of simulations;
sim = 100000;
runlength = j(sim,1,.);
*Size of the Phase II sample;
n = 5;
*design parameters of EWMA control chart;
lambda = 0.1;
L = 2.220;
*Shift;
delta = 0;
stdev = 1;
mean = delta * (stdev/sqrt(n));
*Obtaining the median;
keep = j(2,1,.);
if answer = 1 then r = (m+1)/2;
if answer = 0 then r = m/2;
if answer = 0 then r_1 = (m/2);
if answer = 0 then r_2 = ((m+2)/2);
*Obtaining the value of pr;
pr = (m - r + 1) / (m + 1);
*steady state control limits;
UCL = n*((m - r + 1)/(m + 1 ))+L* sqrt(((n*n)*(r*(m-r+1))/(((m+1)*(m+1))*(m+2)))+(lambda/(2-lambda))*n*(r*(m-r+1))/((m+1)*(m+2)));
LCL = n*((m - r + 1)/(m + 1 ))-L* sqrt(((n*n)*(r*(m-r+1))/(((m+1)*(m+1))*(m+2)))+(lambda/(2-lambda))*n*(r*(m-r+1))/((m+1)*(m+2)));
|
*Generating an IC Phase I sample;
xi = j(m,1,.);
do j = 1 to sim;
* Generating observations from the Normal distribution;
call randgen(xi,‘NORMAL’,0,1);
* Finding the median;
xi_rank = xi || rank(xi);
do l = 1 to m; *For median odd;
if answer = 1 then do;
if xi_rank[l,2] = r then median = xi_rank[l,1];
end;
*For median even;
if answer = 0 then do;
if xi_rank[l,2] = r_1 then keep[1,] = xi_rank[l,1];
if xi_rank[l,2] = r_2 then keep[2,] = xi_rank[l,1];
end;
if answer = 0 then median = sum(keep)/2;
end;
*Calculating the EWMA;
count = 0;
indicator = 0;
zi_1 = n*((m - r + 1)/(m + 1 )); *Starting value;
do i = 1 to 100000000000000000 until (indicator = 1);
count = count + 1;
*Generating a Phase II sample;
yi = j(n,1,.);
*Generating observations from the Normal distribution;
call randgen(yi,‘NORMAL’,mean,1);
*Calculating the precedence statistic;
precedence = j(n,1,0);
do i = 1 to n;
if yi[i,]>median then precedence[i,] = 1;
end;
U = sum(precedence);
*Charting statistic;
zi = lambda*U + (1-lambda)*zi_1;
if (zi < UCL) & (zi > LCL) then do; indicator = 0; end;
if (zi > UCL) | (zi < LCL) then do; indicator = 1; end;
zi_1 = zi;
end;
|
runlength[j,1] = count;
end;
create EWMA from runlength [colname = {RL}];
append from runlength;
proc univariate data = EWMA noprint;
histogram;
inset mean std p5 q1 median q3 p95 / format = 10.2 pos = ne;
run; |
| SAS program number |
Figure title |
Figure number |
| 12 |
SAS output where the design parameters (m = 100, n = 5, λ = 0.10, LCL = 219.5, UCL = 310.5) of the EWMA-rank chart were chosen for a nominal ARLIC = 500 |
4.28 |
| SAS program |
proc iml;
*Size of the IC Phase I sample;
m = 100;
*Number of simulations;
sim = 100000;
runl = j(sim,1,.);
*Size of the Phase II sample;
n = 5;
*Expected value and stdev of W;
exp_w = (n*(n+m+1))/2;
stdev_w = sqrt ( n*m*(n+m+1)/12);
*Design parameters of EWMA chart;
lambda = 0.1;
*Control limits;
Add_subtract = 45.5;
LCL = exp_w - add_subtract;
UCL = exp_w + add_subtract;
*Shift;
delta = 0;
stdev = 1;
mean = delta * (stdev/sqrt(n));
|
do j = 1 to sim;
* Initializing values;
count = 0;
indicator = 0;
zi_1 = exp_W;
xi = j(m,1,.);
zeros = j(m,1,0);
* Generating an IC Phase I sample;
* Generating observations from the Normal distribution;
call randgen(xi,‘NORMAL’,0,1);
xii = zeros||xi;
do i = 1 to 100000000000000000 until (indicator = 1);
count = count + 1;
yi = j(n,1,.);
* Generating a Phase II sample;
* Generating observations from the Normal distribution;
call randgen(yi,‘NORMAL’,mean,1);
*Obtaining the rank‐sum statistics;
ones = j(n,1,1);
yii = ones||yi;
comb = xii // yii;
rank = ranktie(comb[,2]);
comb_rank = comb || rank;
call sort (comb_rank, {2 3}, {3});
W_vec = comb_rank[,1]#comb_rank[,3];
W = sum(W_vec);
*Charting statistic;
zi = lambda*W + (1-lambda)*zi_1;
*Comparing the charting statistics to the control limits (For the two‐sided chart);
if ((zi > = UCL) | (zi < = LCL)) then indicator = 1;
zi_1 = zi;
end;
runl[j,1] = count;
end;
create EWMA from runl [colname = {RL}];
append from runl;
proc univariate data = EWMA noprint;
histogram;
inset mean std p5 q1 median q3 p95 / format = 10.2 pos = ne;
run; |
Some examples of SAS programs for Phase I control charts
SAS program for the Phase I median control chart
proc iml;
* Number of simulations;
z = 100000;
* Number of samples;
m = 5;
* Number of observations;
n = 16;
* LCL;
lcl = 4;
*UCL;
ucl = n-lcl;
* Constant added for the OOC case;
delta = 0;
* Generating observations from the IC N(mu, var) distribution;
* IC mean of Normal distribution;
mu = 0;
* IC variance of Normal distribution;
var = 1;
obs = j(m*z,n,.);
call randgen(obs, "normal", mu, sqrt(var));
do i = 1 to z;
obs[(i*m-(m-1)),] = obs[(i*m-(m-1)),]+delta;
end;
do i = 1 to z;
vector = 0;
apart = j(m,n,.);
apart[1:m,] = obs[(i*m-(m-1)):(i*m),];
do o = 1 to n;
vector = vector//apart[,o];
end;
vector = vector [2:nrow(vector),];
me = median(vector);
do k = 1 to nrow(apart);
do l = 1 to ncol(apart);
if apart[k,l]<me then apart[k,l] = 1; else apart[k,l] = 0;
end;
end;
sum = apart[,+];
signal_ucl = j(nrow(sum),1,.);
signal_lcl = j(nrow(sum),1,.);
do p = 1 to nrow(signal_ucl);
if sum[p,] > = ucl then signal_ucl[p,] = 1; else signal_ucl[p,] = 0;
if sum[p,] < = lcl then signal_lcl[p,] = 1; else signal_lcl[p,] = 0;
end;
signal = signal_lcl||signal_ucl;
at_least = sum(signal);
if at_least>0 then FAP_sum = 1; else FAP_sum = 0;
keep = keep//FAP_sum;
end;
total = sum(keep);
FAP = total/z;
print "The Median chart for normally distributed observations",
lcl ucl,
m [label = ‘Number of samples’],
n [label = ‘Number of observations in each sample’],
z [label = ‘Number of simulations’],
mu [label = ‘mu0’],
var [label = ‘sigmasq0’],
delta,
FAP [format = .4];
SAS program for the Phase I mean-rank control chart
proc iml;
keep = 0;
*Number of simulations;
sim = 100000;
*Number of samples;
m = 45;
*Number of observations in each sample;
n = 10;
*Control limits;
UCL = 2.736;
LCL = -UCL;
*The size of the pooled sample;
upper_N = m*n;
*Expected value of the rank;
exp = (upper_N+1)/2;
*Variance of the rank;
var = ( (upper_N - n) * (upper_N + 1) ) / (12*n);
*Standard deviation of the rank;
stdev = sqrt(var);
do k = 1 to sim;
obs = j(m,n,.);
r_bar_i = j(m,1,.);
zi = j(m,1,.);
*Generating observations from the N(0,1) distribution;
call randgen(obs, "normal", 0, 1);
*Ranking the observations of the pooled sample of size N = mn;
rank_obs = rank(obs);
*Calculating the average rank of each sample;
do l = 1 to m;
r_bar_i[l,] = sum (rank_obs[l,1:n])/n;
end;
*Calculating the standardized values;
do o = 1 to m;
zi[o,] = (r_bar_i[o,] - exp) / stdev;
end;
*Is the chart signalling?;
signal_ucl = j(m,1,.);
signal_lcl = j(m,1,.);
do w = 1 to m;
if zi[w,]> = ucl then signal_ucl[w,] = 1; else signal_ucl[w,] = 0;
if zi[w,]< = lcl then signal_lcl[w,] = 1; else signal_lcl[w,] = 0;
end;
signal = signal_lcl + signal_ucl;
at_least = sum(signal);
if at_least>0 then FAP_one_sim = 1; else FAP_one_sim = 0;
keep = keep // FAP_one_sim;
end;
FAP = (sum(keep))/sim;
print FAP;
