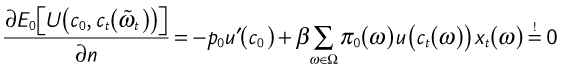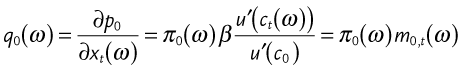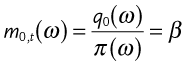Chapter 10 Understanding Valuation Theory
We present the key principles and elements of modern valuation theory, which is the basis of modern pricing, risk, and performance models. We demonstrate how modern valuation theory allows for building valuation models for virtually any instrument from a manageable set of atomic valuation building blocks described in our approach.
10.1 The Purpose of Valuation Theory
Asset pricing is about finding an appropriate value, or a “price” for a financial instrument, an asset. We use the term valuation theory instead of “asset pricing theory” as it is more generic and also points more in the direction of what the theory actually does.
The theory gives an economic rational for the valuation model, so we can justify the results in front of ourselves and our superiors or clients. Giving an economic rational necessarily means working with an economic model, which in turn implies the usage of assumptions and simplifications.
This also points to a practically very important, though often neglected aspect: We talk about a “value” in the first place and not a “price,” because the latter always has a connotation to a market. However, if you have a market price you do not need to value the instrument anymore, right? Just take the market price for the asset and you’re home and safe.
Of course, this does not work for the situations when valuation theory is relevant: illiquid (rarely or not-at-all traded) instruments, for which no readily available market price exists.
So we are left to ourselves to find a value for such instruments. The most simple models—or rather, approaches—would try to look out for similar instruments that are traded and hence have a market price and infer from here a valuation to our illiquid case. But, how appropriate or safe is that? Many financial instruments, in particular the illiquid ones, are quite unique, and often have very pricing-relevant aspects, such as risk factors, guarantees or embedded optionality. So, finding a “similar but traded” instrument, or—better—set of instruments, though simple in conception, it is a daunting task when trying to implement it.
There is even a theory that formalises a variant of this idea of linking an instrument to another instrument, the so-called Capital Asset Pricing Model (CAPM),1 which, in its basic form, stipulates a constant relationship between the relative movement of an instrument price to the relative movement of market portfolio. Although the theory is nice, it is a theory. The practical obstacles of bringing it to life are enormous, starting from finding the right market portfolio to a series of simply unjustifiable assumptions about the behaviour of asset prices.
As a reaction, financial theorists have embarked in ever more complicated econometric pricing models, trying to get rid of restrictive assumptions here and there, but so far with very limited success, to say the least.
We therefore recommend that, before blindly following whatever is taught at universities today, you should sit back for a second and think of what you really need the valuation for.
- Is it because you want to find a true value for a traded instrument to be able to exploit market inefficiencies (i.e., you would buy it, if the market value is below the estimated true value)?
- Is it because you are forced by some sort of regulator to mark-to-market your instrument for risk management purposes? The question here is how useful such a marking-to-market of an illiquid security to a nonexistent market could be. What type of information would you generate here?
What appears obvious is that valuation has always a lot to do with subjective judgement. Choosing a model, selecting the implementation parameters, the relevant question is always: “What is the instrument worth to me or my institution?”
This brings us to another important, but often neglected, dialectic of subjective versus market pricing. Much (if not most) of academic valuation theory fares under the heading of arbitrage pricing, claiming that there is perfect information and competition in financial markets, which themselves are assumed (for the theory to work) to be complete; that is, any type of cash flow can be traded at all types in every possible level of decomposition.
Well, if we learned one thing in the past year, it’s that markets are not perfect and there is not always somebody out there willing to exploit any type of (even implied) inefficiency.
So what works under conditions such as the ones prevailing in the current crisis? In our opinion, the one and only true anchor you have when valuing instruments is their cash flow structure, which means real income and repayment to you. To find a value using (expected) cash flows, they need to be discounted properly to take into account both the time value of money (having the same amount of money today is worth more than having it tomorrow, as in the meantime you could earn interest on it) and the opportunity cost of holding that instrument. An additional value diminishing factor is the probability that the issuer of the instrument is actually not going to pay future cash flows, the probability of issuer default. Discounting is done by constructing so-called discount curves that need to incorporate all three aspects.
The valuation approach using this is called the Discount Cash Flow valuation approach, and it is applicable to all types of instruments. We therefore follow Damodaran, if he claims that Discounted Cash Flow valuation is the king path to valuation: “While discounted cash flow [] valuation is only one of the three ways of approaching valuation [which are DCF; relative and contingent claim valuation] and most valuations done in the real world are relative valuations, it is the foundation on which all other valuation approaches are built.” (Damodaran, 2002, p.11)
This statement gives then also the tenor for this chapter in which we present to you that part of modern valuation theory that turns around DCF valuation, giving some economic rational to it, and also enlightens the logic of curve construction and discounting.
10.2 Some Notations and Concepts
Valuation theory is developed in a formal language to which we will introduce you bit by bit. We start here by introducing some key symbols and formal conventions that you used throughout this book.
Mathematical Secretism?
We now enter the realm of formal language where most of asset pricing takes place. Therefore a word of comfort to those not yet intimate to the intricacies of mathematical formalism and concepts is warranted: Mathematics, or formal language, is not a secret language designed to make your life miserable and to expose a potential lack of knowledge—it is to help you!
It is easier to write y = f(x), f′(x) > 0 ∀x instead of saying “y is a positive function of x over the full domain of x.”
Therefore, bear with us through this chapter and try to get used to the most relevant set of formal concepts in the world of finance. In the spirit of Chiang and Wainwright (2005) we will do our best to keep you on board and to explain in detail what needs to be explained and simplify as much as possible what can be simplified, at least when it comes to practical application.
10.2.1 On the Use and Meaningfulness of Models
Throughout this book we presented and worked with a series of economic models. When working with them, you should always keep in mind the following caveats.
Models are never an exact description of what actually happens, but rather logical frameworks that help structure your thinking when interpreting real data. Giving models a mathematical formulation often allows us to derive implications of a certain setting/scenario that are not necessarily visible at first sight. Often we also are able to exclude certain interpretations that are not consistent with the chosen framework.
These implications/exclusions are, however, valid only if the assumptions of the model framework are correct. Correct means that they adequately reflect the driving forces of actors’ motivations and interactional logic.
The ultimate test for every model is when it is confronted with real data or tested. Still, not being able to reject a model base on real data does not necessarily mean that it is true. It is simply not (yet) falsified. With Karl Popper we say that there is no true model, but only models or theories that have not yet been falsified.
It is important to recall this fundamental scientific wisdom, as—particularly in practical work—models all too often are taken for granted, providing “the truth.” When working with models, you should always be wary of them, taking the rich help they can give you but never really trusting them.
10.2.2 Random Variables
A random variable or “statistic” is a concept that allows you to capture the fact that for many aspects in life we have to deal with uncertainty. It represents a conceptual shell for a measure of some aspect of real life that may take on any of a predefined set of possible, mutually exclusive values, its domain. The assignment of a concrete value to a previously random variable, the realisation, is dependent on a specific event, usually determined by the definition of the random variable. Each of the possible values of a domain may be assigned a probability according to which might become the realisation of the random variable. The distribution of probabilities over possible values is called the probability distribution of the random variable. Hence, a random variable may be fully characterised by its domain and the corresponding probability distribution.
Let’s make this a bit more lively: Think of the random variable “weather tomorrow” that may take on the values “same as today,” “better,” or “worse.” The event that will assign the value to that random variable is the emergence of “tomorrow,” because then we will clearly know how the weather is in relation to “today” (then “yesterday”).
This example also nicely shows the importance of the domain definition for the meaningfulness of a random variable, as you equally could have assigned the possible values “rain,” “sunshine,” and “snow.” Although the event in both cases will bring along the information you need to assign a value to the random variable, the transformation from observed weather tomorrow into one of the measures defined by the two domains fundamentally determines the meaning and information content represented by the variable.
The example also illustrates the importance of the mutually exclusive property of the values in the domain. This important specification means that nature at any one time can only take on one state of the random variables domain. Think of a domain for the random variable “weather tomorrow” that consists of the states “rain,” “fog,” and “sunshine.” Even though “sunshine” is well enough a state on its own, the state “fog” may imply additionally that it rains! Hence, the information content of the domain is flawed.
The most common example for a random variable is the value of a die. Here, the domain is clearly one of the numbers {1,2,3,4,5,6} and the event determining which of the numbers will be the value is the throwing of a die. The example usually is used in statistics text books to illustrate random variables but its experimental nature does, by construction, not exhibit the typical problems encountered with random variables in financial practice.
We may say that a lot (if not every) of financial aspects of a financial instrument may (need to) be expressed as a random variable, as even promised cash flows may need be paid out due to defaulting to the counterparty or other unforeseen events.
In finance, typical random variables are the:
Which distribution is the right one for a given random variable is the subject of an academic field of its own: probability or stochastic theory. In practice, it is often not easy to decide which is the right probability distribution. Except for very few obvious cases, like the rolling of a die or the throwing of a coin, the probability distribution of a random variable is a matter of subjective judgement often assisted by some stochastic (or econometric) modelling of an underlying but unknown process that drives the emergence of this or that value for a random variable. Who could know with certainty with which probability the weather tomorrow will take on this or that form?
This brings us to a fundamental problem when working with random variables in finance. Although we reasonably assume that there exists a true distribution for the concepts we identify, we do not know it and must make an assumption-based approximation. In this book, we made it explicit in the various pricing approaches how they solve this dilemma by which assumptions, and the potential consequences of these, for the exactness of the pricing method.
10.2.3 Time and Its Notation
Intertemporal considerations are key to asset pricing, which turns around relating a series of future (and sometimes past) cash flow events to a current, or reference, date. Hence, it is important to clarify the time concepts and corresponding notation.
Throughout the book, we tried to limit our discussion to discrete random variables, closely linked with the concept of discrete time measurement. The reason is that these, first, are easier to understand, and second, capture the same concepts as continuous random variables.
Since pricing is always done from a relative perspective—that is, seeking to determine the asset price for a given reference date, around which all other relevant events are ordered and measured—we also model time in a relative way. Out of a series of dates t = {−tT, …, −t2, −t1, 0, t1, t2, …, tT} we denote by t = 0 as the reference or pricing date (we might be tempted to call this date “today”). This logic is illustrated in Figure 10.1.
In line with market conventions, we measure difference in time as the year fraction between two dates. Calendars have the unpleasant feature to be rather inhomogeneous (some months are 28, 29, 30, or 31 days in length), so the term year fraction is not a standardised concept. Rather, we must resort to a so-called day count convention that specifies the exact method to transform two dates into a year’s fraction. There exist quite a number of day count conventions that are in use in the markets.
The most straightforward one is the rule ACT/ACT, which counts the number of actual calendar days between two dates and divides it by the actual number of calendar days in the current year. A related method is ACT/365, which always divides the first term of ACT/ACT by 365, even if the current year has 366 days. As these methods could reach widespread usage only with the emergence of computers, quite a number of simpler methods have been designed and are still in use.
In this book, however, we abstract from specific day count conventions by denoting the year fraction between two dates t1 and t2 as Δ(t1,t2), whatever may be the day count convention to be used. In addition, with reference to the central date t = 0 we specify Δ(t) = Δ(0,t) making the formulation of certain formulas less heavy without any loss in precision.
10.2.4 Discount Factor and Future Value
Future values do not have the same relevance today that current values do. Think of a cake that you can eat tomorrow, but not today. Although you will still appreciate the outlook (if you like cakes), today’s utility will be diminished by the fact that you have to wait another day to eat the cake.
Similarly, you can say that about money (cash flow) you will earn tomorrow, but not today. In the context of investing, another aspect becomes relevant: Money you have today can be invested and will bring you additional income, whereas money you have available only in the future cannot obviously be invested today. We call this concept the opportunity cost of time, the cost you incur due to the fact that the money is only available in the future is equal to the lost income. …
Hence, we may say in general that from today’s perspective, future values are worth less today than they are tomorrow. The depreciation of future values to have their current day equivalent is captured by the concept of a discount factor.
We denote the discount factor that transforms a future cash flow xt, t > 0 to get its value equivalent at date t = 0 as m0,t ∀t. By construction m0,t < 1. As there is no depreciation for current values we have m0,0 = 1.
However, there is no general rule what the “right” discount factor should be. As you will see next, determining the discount factor is one of the key issues when pricing an asset. To make things worse, the uncertainty inherent in future cash flows often makes even the discount factor uncertain from the perspective of the investor and, hence, a random variable.
10.3 The Mother of All Valuation Formulas
At its very heart, valuation theory was developed to operationalise the fundamental statement “the price of an instrument should equal the present value of its expected future cash flows it generates.”
We start with developing an intuition of this by asking ourselves what the relevant elements of this statement are. The term “equal to” tells us that we have to formulate the problem in the form of an equation. On the left-hand side of the equation, there is the price of the instrument, call it pt, the determinants of which we try to model. As we take the perspective of date t = 0, we may write the equation as p0 = ?.
Things are more difficult on the right-hand side of the equation. What is meant by “present value of expected future cash flows”? Assume for the moment2 that the instrument generates only one future cash flow at date t, t > 0.
- From the perspective of t = 0 the future cash flow is unknown, so we need to treat it as a random variable
 with domain X. Here, some may object that there are in fact assets where the (series of) future cash flow(s) is agreed upon at contract conclusion and, hence, is not really unknown. Classical examples are zero or straight coupon bonds. This is correct, but in particular from a risk management perspective, we should never forget that these future cash flows are “only” contractual agreements, and even if they are guaranteed by a third party to the contract, we can never be 100% certain that you will actually get the money in the exact amounts agreed upon. Even with the safest investment there does always exist a tiny probability of default, or nonpayment, or—at least—a reduction in amounts being paid. So, it is fair to treat the future cash flow as random and our analytical framework holds.
with domain X. Here, some may object that there are in fact assets where the (series of) future cash flow(s) is agreed upon at contract conclusion and, hence, is not really unknown. Classical examples are zero or straight coupon bonds. This is correct, but in particular from a risk management perspective, we should never forget that these future cash flows are “only” contractual agreements, and even if they are guaranteed by a third party to the contract, we can never be 100% certain that you will actually get the money in the exact amounts agreed upon. Even with the safest investment there does always exist a tiny probability of default, or nonpayment, or—at least—a reduction in amounts being paid. So, it is fair to treat the future cash flow as random and our analytical framework holds. - In many cases, there is no explicit cash flow agreed between the investor in an asset and the issuer. For example in the case of equity shares or fund shares the investor has no guarantee that he or she will receive any income on that asset. However, the investor always has the possibility to resell the asset, making the future cash flow the unknown price he or she may expect to get.
- Having found a formulation for future cash flow, we can now turn to the statement “present value of …”. It implies that from the perspective of t = 0, not the cash flow
 itself, but some transformation of it, call it
itself, but some transformation of it, call it  , is to equal the current price. We will discuss this transformation at length later in this chapter. For now, it may be enough to know that this transformation is linear; that is,
, is to equal the current price. We will discuss this transformation at length later in this chapter. For now, it may be enough to know that this transformation is linear; that is,  , and that the transforming factor is called discount factor. It has the subscript “0,t” as it performs a transformation from date t to date 0. In addition, at date t = 0 we do not know the exact value of the discount factor, as—we will see that later—it depends on the consumption level at date t, which itself is a function of
, and that the transforming factor is called discount factor. It has the subscript “0,t” as it performs a transformation from date t to date 0. In addition, at date t = 0 we do not know the exact value of the discount factor, as—we will see that later—it depends on the consumption level at date t, which itself is a function of  . Hence, we must also treat m0,1 as a random variable, leading to the stochastic discount factor
. Hence, we must also treat m0,1 as a random variable, leading to the stochastic discount factor  .
. - The last missing element on the right-hand side is a formulation of the term “expected.” As both, the discount factor
 and the ultimate cash flow
and the ultimate cash flow  are not known at date t = 0 we must build an expectation of their values using the information available at date t = 0, to be able to determine the current price, p0. We express this by applying the expectation generating function E0[].
are not known at date t = 0 we must build an expectation of their values using the information available at date t = 0, to be able to determine the current price, p0. We express this by applying the expectation generating function E0[].
With these considerations, the initial statement may be expressed as
(10-1) ![]()
where:
- p0price of the asset at the reference date t = 0
 unknown future cash flow due on date t > 0
unknown future cash flow due on date t > 0 stochastic (random) discount factor transforming the future cash flow
stochastic (random) discount factor transforming the future cash flow  into a value at date t = 0; that is, its “present value”
into a value at date t = 0; that is, its “present value”- E0[]expectation generating function for the two random variables
 and
and  , using the information available at date t = 0
, using the information available at date t = 0
Equation (10-1) is called the Central Pricing Equation. It sets the scene for an important amount of theoretical and empirical research about investor behaviour and asset price setting in financial markets.3 Most of valuation theory consists of specializations and manipulations of this formula. Despite its apparent simplicity, it is a very powerful tool that logically derives a fundamental relationship valid for any instrument price observed.
Figure 10.2 shows the various areas of valuation theory, all centred around the Central Pricing Equation. We approach this by presenting, step by step, the key areas in financial theory that bring subsequently a clearer picture on what is behind each of the elements in the Central Pricing Equation:
- Consumption-based theory models the investor’s preferences and derives a structural discount factor formulation.
- Contingent claim analysis explicitly models a set of possible future cash flows. Discount factor is interpreted as the relative subjective value given by the investor to a particular state of nature.
- Arbitrage pricing theory analyses the question of whether and under which conditions an equilibrium market price exists and how it is connected to the central pricing equation.
For the reasons mentioned in Section 10.1, we will not explore the intellectually very interesting area of arbitrage pricing theory. The valuation approach we present here is fundamentally investor-oriented: For a given illiquid asset, the investor needs to make up his or her mind what an instrument is worth. By doing so he or she should already duly take repayment risks and opportunity costs into account. The question of whether this value can also be seen as a hypothetical market price is, in our opinion, not the most important at this stage.
10.4 Consumption-based Theory
We start with developing an explicit formulation of the stochastic discount factor ![]() based on a relatively simple model of investor behaviour. Consumption-based theory takes the point of view of an investor, asking for what effect an investment at date t = 0 could have on his or her current and expected future levels of consumption. The investment is assumed to be made by purchasing a financial instrument that is going to produce an (from the t = 0 perspective) uncertain future cash flow
based on a relatively simple model of investor behaviour. Consumption-based theory takes the point of view of an investor, asking for what effect an investment at date t = 0 could have on his or her current and expected future levels of consumption. The investment is assumed to be made by purchasing a financial instrument that is going to produce an (from the t = 0 perspective) uncertain future cash flow ![]() , t > 0. At date t = 0, the investor must decide how much to save now (t = 0) and invest in a number n of instruments, each producing the uncertain cash flow
, t > 0. At date t = 0, the investor must decide how much to save now (t = 0) and invest in a number n of instruments, each producing the uncertain cash flow ![]() , while reducing the present day consumption.
, while reducing the present day consumption.
We look at this problem in a two-date (t = 0; t > 0) context. This setting is quite realistic for many investment situations4 since we do not specify the exact length of the interval between the two dates.
Suppose that the investor has a fixed noninvestment income over time that guarantees a time-independent fixed consumption level at all dates. The investor’s default position would then be not to buy the instrument and to have access to a fixed (monetary) level of consumption, c*, implied by noninvestment income.
At date t = 0, the investor’s consumption level in monetary terms is therefore
where p0 is the price of the instrument and n is the number of instruments the investor decides to buy.
The future consumption level, ct, t > 0, is not known, because it depends on the uncertain cash flow to be generated by the investment. So, from the perspective of t = 0, the future consumption level is again a random variable, ![]() , which is determined by
, which is determined by
Here, ![]() is the cash flow generated by a single instrument, and n is the number of instruments purchased at date t = 0.
is the cash flow generated by a single instrument, and n is the number of instruments purchased at date t = 0.
The two preceding equations described the budget constraints of the investor, who has to decide how many instruments (n) to buy. The decision criterion for the investor is his or her inter-temporal utility over present and future consumption levels. We write this inter-temporal utility as
Before entering the detailed decision problem in Section 10.4.3, we first have a look at the concept of utility and its operationalisation via a utility function in the next section.
10.4.1 Utility Functions and Investor Preferences
The investor needs to make sure that he or she draws the maximum utility, or pleasure, from his or her inter-temporal decision. Obviously, with unknown future values of wealth, and hence, consumption, this is a difficult one.
In formal language we use utility functions to summarize a consumer’s behaviour by mapping the space of possible consumption bundles C to the real line R. The mapping is ordered in such a way that a higher value on the real line stands for a consumption bundle c, which is preferred by an individual to a consumption bundle c′ with a lower value on the real line. Formally, this is
Working with actual consumption bundles (i.e., with bundles of goods) that may be consumed is realistic, but very unhandy in practice. We therefore prefer to refer to monetary consumption levels; that is, the monetary cost of goods being consumed.
It can be shown that if the preference ordering is complete, reflexive, transitive, and continuous—in short, representing a rationally behaving individual—it can be represented by a continuous utility function.
Figure 10.3 shows the classical form of a stylised continuous utility function over monetary consumption levels c, u(c). It has the property that its first derivative is positive and the second derivative negative:
 : The marginal utility of any consumption level is always positive, reflecting a desire for more consumption: People always want to consume more. The marginal utility is the infinitesimal (very small) change in utility due to a change in consumption.
: The marginal utility of any consumption level is always positive, reflecting a desire for more consumption: People always want to consume more. The marginal utility is the infinitesimal (very small) change in utility due to a change in consumption.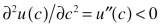 : The marginal increase in utility is decreasing or constant, reflecting the declining marginal value of additional consumption. The last bite is never as satisfying as the first.
: The marginal increase in utility is decreasing or constant, reflecting the declining marginal value of additional consumption. The last bite is never as satisfying as the first.
Functions with this property are called concave, hence we speak of a concave utility function.5 An important property of utility functions is that any monotonic transformation of such a function represents the same preferences. Formally, if u(c) represents some preferences c ≻= c′ and f:R → R is a monotonic function (i.e., has no breaks or steps in it), then f(u(c)) will represent exactly the same preferences since f(u(c)) ≥ f(u(c′)) if and only if u(c) ≥ u(c′).
On the Use of Monetary Amounts Instead of Real Quantities
From a purely theoretical perspective, we may argue that the utility expressed as a function of consumption rather depends on the quantity of physical goods than their monetary value. This would have the advantage that a unit of a consumption good can be used as a common denominator valid at all dates.
In practice, however, working with physical good representations brings along a rat-tail of significant data availability and measurement problems.
In addition, although the usage of physical goods may be of benefit for theoretical work on investor behaviour, the testing of these models usually is done using monetary measures, as they are more readily available and directly comparable.
It often is assumed in the literature therefore that the inflation rate is negligible with respect to the movements of asset prices (see, e.g., Cochrane 2001, Chapter 2). The introduction of the consumption plans for a physical good into the optimization objective indicates that this approach is not designed for direct use by fund managers. Instead, it is more suitable for individual behaviour analysis, for building macro dynamic models that link the real and financial sectors under the assumption of a representative agent, or else for asset pricing.
In the context of uncertainty, when the utility over uncertain future consumption levels is measured, it can be shown that the expected utility over various possible monetary consumption levels must be in additive form. Consider the following situations:
- 1. In the first situation, you consume c1 with probability π and c2 with the (remaining) probability 1 – π: (π → c1, (1 − π)→ c2).
- 2. In the second situation, you consume c1 with probability θ and c2 with the (remaining) probability 1 − θ : (θ → c1, (1 − θ)→ c2).
It can be shown6 that there exists a continuous utility function u that describes the consumer’s preferences; that is (π → c1, (1 − π)→ c2) ≻ (θ → c1, (1 − θ) → c2) if and only if u(π → c1, (1 − π) → c2) > (θ → c1, (1 − θ) → c2)
This utility function u( ) is not unique; any monotonic transform would do as well.
Under some additional hypotheses, we can find a monotonic transformation of the utility function that has the very convenient expected utility property:
The expected utility property says that the utility of a lottery is the expectation of the utility from its prizes. We can compute the utility of any lottery by taking the utility that would result from each outcome, multiplying that utility times the probability of occurrence of that outcome, and then summing over the outcomes. Utility is additively separable over the outcomes and linear in the probabilities.
Interpretation of Utility Functions
As you might have guessed from the many assumptions already needed, utility functions should not be over interpreted and mostly provide a convenient way to find an ordinal sorting of options and hence derive individual behaviour.
In particular they should not be given any psychological interpretation. The only relevant feature of a utility function is its ordinal character.
10.4.2 Risk Aversion and Risk Neutrality
Utility functions can be used to represent the attitude of investors toward risk. The expected utility property applies in particular in the case that uncertainty is with respect to different amounts of money; that is, cash flows an individual may receive under different circumstances (“states of nature”).
It is hence possible to describe an individual’s behaviour who is faced with uncertainty concerning future monetary outcomes, if we only know this particular representation of his or her utility function for monetary consumption levels. For example, to compute the consumer’s expected utility in the situation (π → c1, (1 − π)→ c2), we just need to look at the corresponding expected utility πu(c1) + (1 − π)u(c2).
This construction is illustrated in Figure 10.4 with π = 0.5. Notice that in this example the individual prefers to get the expected value rather than being exposed to the uncertain situation (“lottery”). That means that for the investor, the utility of the lottery u(π → c1, (1 − π) → c2) is less than the utility of the expected value of the lottery, πu(c1) + (1 − π)u(c2). Such a behaviour is called risk aversion.7

Figure 10.4: Expected utility of a lottery. The expected utility of the lottery is 0.5u(c1) + 0.5u(c2). The utility of the expected value of the gamble is u(0.5c1 + 0.5c2). In this case, the utility of the expected value is higher than the expected utility of the lottery, so the individual is risk averse.
If an individual consumer is risk averse, the line drawn between any two points of the graph of his or her utility function must lie below the function. This is equivalent to the mathematical definition of a concave function. It implies that an agent prefers averages to extremes; this is equivalent to risk aversion. Hence, concavity of the expected utility function is equivalent to risk aversion.
It is often convenient to have a measure of risk aversion. Intuitively, the more concave the expected utility function, the more risk averse the consumer. Thus, we might think we could measure risk aversion by the second derivative of the expected utility function that measures the curvature, or concavity of the function. However, this definition is not invariant to changes in the expected utility function: if we multiply the expected utility function by 2, the consumer’s behaviour doesn’t change, but our proposed measure of risk aversion does.8 However, if we normalize the second derivative by dividing by the first, we get a reasonable measure, known as the Arrow-Pratt measure of (absolute) risk aversion:
An important special case is the risk-neutral individual: Risk-neutrality implies that the consumer is indifferent between a sure expected value and the expected utility of it. Formally, this is expressed by a linearly increasing utility function:
The implication of this situation is shown in Figure 10.5. A risk neutral individual is indifferent on whether he or she gets the expected value of a lottery or the lottery itself.
10.4.3 The Investor’s Decision
With the utility function toolkit at hand, we can now formulate the investor’s decision problem at date t = 0.
Using the formulations for c0 in Equation (10-4) and ![]() in Equation (10-5), we model the investor by the expected utility function defined over current and future values of consumption:
in Equation (10-5), we model the investor by the expected utility function defined over current and future values of consumption:
From Equation (10-4) we know that the future consumption ![]() is random as it depends on the future cash flow
is random as it depends on the future cash flow ![]() . Discounting the future by β, 0 ≤ β ≤ 1t captures impatience, and β is called the subjective discount factor. Note that we use the expectation generator E0[] to account for uncertain states and their probabilities. In Section 10.5 we will make this formulation more explicit.
. Discounting the future by β, 0 ≤ β ≤ 1t captures impatience, and β is called the subjective discount factor. Note that we use the expectation generator E0[] to account for uncertain states and their probabilities. In Section 10.5 we will make this formulation more explicit.
Because we do not want to enter a structural discussion of the Central Pricing Equation,9 it will suffice to make the standard concavity assumptions about the utility function; that is, the direct utility function u( ) is increasing, reflecting a desire for more consumption, and concave, reflecting the declining marginal value of additional consumption units.
In line with Section 10.4.2, this formalism captures our investor’s impatience and his or her aversion to risk. Both assumptions are enough to derive an optimum characterisation of the investor’s inter-temporal decision.
Our objective is to find the value at time t = 0 of the single future cash flow ![]() , t > 0. This future cash flow structure consists of the future price of the instrument at date t,
, t > 0. This future cash flow structure consists of the future price of the instrument at date t,![]() and (possibly) an additional income flow
and (possibly) an additional income flow ![]() ; that is,
; that is, ![]() .
.
Assuming that the investor can freely buy or sell as much of the payoff ![]() as he or she wishes, how much will he or she buy or sell? The problem is to find the optimal number of assets n* that maximises the inter-temporal utility, Equation (10-6), under the constraint that this investment will decrease the current consumption level in t = 0, c0. Formally this is
as he or she wishes, how much will he or she buy or sell? The problem is to find the optimal number of assets n* that maximises the inter-temporal utility, Equation (10-6), under the constraint that this investment will decrease the current consumption level in t = 0, c0. Formally this is
Substituting the constraints into the objective function, and setting the derivative with respect to n equal to zero,10 we obtain the first-order condition for an optimal consumption and portfolio choice,
The investor continues to buy or sell the instrument until the marginal loss equals the marginal gain. The investor buys more or less of the instrument until this first-order condition holds. Equation (10-6) expresses the condition for an optimum:
- p0 u′(c0) is the marginal loss in utility if the investor buys another unit of the instrument
 is the marginal expected increase in (discounted) utility the investor obtains from the extra payoff at t
is the marginal expected increase in (discounted) utility the investor obtains from the extra payoff at t
The marginal utility loss of consuming a little less today and buying a little more of the instrument should equal the marginal utility gain of consuming a little more of the asset’s payoff in the future.
If the price and payoff of the asset do not satisfy this relation, the investor will adapt the amount of the asset he or she holds (i.e., buy more or less of the asset) and, hence, implicitly adjust the amount of consumption.
As c0 is known, we can say that u′(c0) = E0[u′(c0)] and therefore write
It follows that the asset’s price should equal the expected discounted value of the asset’s payoff, using the investor’s marginal utility to discount the payoff.
You may have noticed that Equation (10-7) is actually very close to the Central Pricing Equation. Indeed, if we define the stochastic discount factor
Then, we again get the basic pricing formula, Equation (10-7):
From Equation (10-9) we see that the discount factor is a function of a random variable ![]() , is a random variable itself, and hence follows a distribution. From Equation (10-4) we know that
, is a random variable itself, and hence follows a distribution. From Equation (10-4) we know that ![]() is a function of
is a function of ![]() and so it is
and so it is ![]() . This means that
. This means that ![]() and
and ![]() are correlated.
are correlated. ![]() is hence called stochastic (another word for random) because it is not known with certainty at time t = 0. Because of Equation (10-8),
is hence called stochastic (another word for random) because it is not known with certainty at time t = 0. Because of Equation (10-8), ![]() also often is called the marginal rate of substitution, the rate at which the investor is willing to substitute consumption at time t for consumption at time t = 0. net.
also often is called the marginal rate of substitution, the rate at which the investor is willing to substitute consumption at time t for consumption at time t = 0. net.
Example: The Marginal Rate of Substitution (MRS)
Let, u(c) = u(c0, ct) be an inter-temporal utility function of present (t = 0) and future (t > 0) levels of consumption. Suppose that we increase the future level of consumption ct; how does the consumer have to change his or her consumption at date t = 0 in order to keep the inter-temporal utility constant?
Let dc0 and dct be the changes in c0 and ct. By assumption, the change in utility must be zero, so
This expression is known as the marginal rate of substitution between consumption levels c0 and ct. The marginal rate of substitution does not depend on the utility function chosen to represent the underlying preferences.11
10.4.4 Multiple Periods
So far, we have analysed the investor’s decision in a two-date (or two-period) context. We pointed out that this setting captures a wide range of practical situations, in particular if we interpret ![]() . Using this, we can now formally show that the central pricing equation holds for any two periods of a multi-period model.
. Using this, we can now formally show that the central pricing equation holds for any two periods of a multi-period model.
Think of the future cash flow ![]() , consisting of the future price
, consisting of the future price ![]() and, possibly, an income cash flow
and, possibly, an income cash flow ![]() , all random variables, unknown at date t = 0. This formulation allows us to think of multi-period pricing problems in just two-period contexts.
, all random variables, unknown at date t = 0. This formulation allows us to think of multi-period pricing problems in just two-period contexts.
In situations, however, where a set of future cash flows is prescheduled and hence known at date t = 0, we will want to relate a price to an entire cash flow stream, rather than just to one dividend and next period’s price.12 Using the consumption-based approach, we extend Equation (10-5) to a multi-period utility function,
Note that, as β0 = 1, for T = 1, this is exactly the two-period utility function of Equation (10-4). As with the two-period model, the investor’s first-order condition gives the pricing formula:
which for T = 1 is equivalent to the two-period Central Pricing Equation. An interesting formulation of Equation (10-11) is obtained when using ![]() incrementally to derive a series of future cash flows.
incrementally to derive a series of future cash flows.
Acknowledging ![]() and extending the logic for
and extending the logic for ![]() ,
, ![]() , … etc., this is equivalent to the formulation in Equation (10-10).
, … etc., this is equivalent to the formulation in Equation (10-10).
10.5 Contingent Claim Analysis
The consumption based theory introduces a framework for the interpretation of the stochastic discount factor ![]() as the marginal rate of substitution between current and future consumption. It says little, however, about the uncertainty inherent to the future cash flow
as the marginal rate of substitution between current and future consumption. It says little, however, about the uncertainty inherent to the future cash flow ![]() and how to deal with this uncertainty. This is the contribution of contingent claim analysis, which explicitly models and analyses the effect of uncertainty and the corresponding expectation building. Historically, contingent claims analysis allowed extending the relationship between competitive equilibriums and welfare optimality to an economy operating under uncertainty. Arrow (1953, reprinted 1964) introduced uncertainty into a pure-exchange economy via a random variable designating the “state of nature,”
and how to deal with this uncertainty. This is the contribution of contingent claim analysis, which explicitly models and analyses the effect of uncertainty and the corresponding expectation building. Historically, contingent claims analysis allowed extending the relationship between competitive equilibriums and welfare optimality to an economy operating under uncertainty. Arrow (1953, reprinted 1964) introduced uncertainty into a pure-exchange economy via a random variable designating the “state of nature,” ![]() . Debreu (1959) extended Arrow’s pure exchange model in important ways, hence the name “Arrow-Debreu” to describe the contingent claims economies and related concepts.13
. Debreu (1959) extended Arrow’s pure exchange model in important ways, hence the name “Arrow-Debreu” to describe the contingent claims economies and related concepts.13
10.5.1 States of Nature and Contingent Claims
We start with formalising the concept of an ex ante unknown “state of nature at date t.” By ex ante we mean from the point of view of any date prior to t.
The “state of nature at date at date t” concept satisfies the definition for a random variable in Section 2.2. We denote this random variable as ![]() with a domain set Ω = {ω1, ω2, …, ωΩ} containing Ω mutually exclusive states of nature that may occur at the future date t. A particular realisation of
with a domain set Ω = {ω1, ω2, …, ωΩ} containing Ω mutually exclusive states of nature that may occur at the future date t. A particular realisation of ![]() is ωt, being one of the elements in Ω; that is, ωt ∈ Ω. The exact value ωt is not revealed until date t, hence the time-specific subscript.
is ωt, being one of the elements in Ω; that is, ωt ∈ Ω. The exact value ωt is not revealed until date t, hence the time-specific subscript.
In its earliest formulations, contingent claim analysis considered states representing physical conditions of the environment; for example, “rain” or “shine.” But the notion of a state soon became and can be more broadly interpreted as representing other forms of uncertainty in financial markets, such as “issuer default,” “underlying price above/below strike price,” and so on.
The set-up is depicted in Figure 10-6 where, at date t = 0, the future state is unknown and represented by the random variable ![]() . At a date t > 0 a specific value from the domain Ω emerges.
. At a date t > 0 a specific value from the domain Ω emerges.

Figure 10.6: Two-period (date) example of the random variable “state of nature at date t,” ![]() . At date t = 0, its value is unknown, but one of three possible states, either
. At date t = 0, its value is unknown, but one of three possible states, either ![]() ,
, ![]() , or
, or ![]() , is revealed at date t.
, is revealed at date t.
Given ![]() , a contingent claim is defined as a contractual claim on a unit monetary cash flow (e.g., one Euro or one Great Britain Pound). These claims are traded and agreed upon at date t = 0, prior to the realization of state
, a contingent claim is defined as a contractual claim on a unit monetary cash flow (e.g., one Euro or one Great Britain Pound). These claims are traded and agreed upon at date t = 0, prior to the realization of state ![]() . It can be shown14 that this trading results in a competitive equilibrium and hence the resulting outcome is stable. At date t, trading stops, the state of nature, ωt, is revealed, and only those contingent claims that are conditional on the realized state,
. It can be shown14 that this trading results in a competitive equilibrium and hence the resulting outcome is stable. At date t, trading stops, the state of nature, ωt, is revealed, and only those contingent claims that are conditional on the realized state, ![]() , are paid out.
, are paid out.
In the case where a certain state of nature ωt materialises at date t > 0, the corresponding contingent claim pays one monetary unit, and zero otherwise. Formally, this is expressed as
Due to their contractual nature, contingent claims may be interpreted as elementary securities. Elementary securities generate a cash flow only in one single state of nature. Contingent claims are elementary securities with the special feature that their cash flow is a unitary value. We will use this important property in the next section.
In his 1953 article, Arrow assumed that there exist precisely as many contingent claims as there are possible states of nature, with states being mutually exclusive15 so that only one of all possible states can materialise at date t.
In this setting, the Ω-dimensional payoff vectors of contingent claims, each claim paying off 1 monetary unit if ![]() and zero in all other states, are linearly independent. The matrix of claim-specific unitary cash flows may be represented by a Ω-dimensional identity matrix
and zero in all other states, are linearly independent. The matrix of claim-specific unitary cash flows may be represented by a Ω-dimensional identity matrix
The contingent claims in this particular setting are called Arrow-Debreu securities, ![]() .
.
10.5.2 Contingent Claims and Cash Flows
Contingent Claims Analysis further distinguishes between the unit monetary contingent claims, ![]() , and the actual cash flows that are generated if a given state is adopted. Each state ω corresponds to a specific cash flow, xt(ω), out of a set of possible cash flows X. At date t = 0, the actual cash flow generated at t = 0 is unknown and hence modelled as a random variable
, and the actual cash flows that are generated if a given state is adopted. Each state ω corresponds to a specific cash flow, xt(ω), out of a set of possible cash flows X. At date t = 0, the actual cash flow generated at t = 0 is unknown and hence modelled as a random variable ![]() .
.
The various realisations of ![]() may be mapped to states of nature
may be mapped to states of nature ![]() . Denote this mapping as
. Denote this mapping as ![]() . The mapping from
. The mapping from ![]() to
to ![]() ,
, ![]() , is non-reflexive, meaning that for each ω in Ω one may exactly identify a specific x, but not the other way around. It is therefore possible that multiple states of nature result in the same payment! This is illustrated in Table 10.1, where two states, ω1 and ω3, result in the same cash flow, x1. Formally, this may be expressed as
, is non-reflexive, meaning that for each ω in Ω one may exactly identify a specific x, but not the other way around. It is therefore possible that multiple states of nature result in the same payment! This is illustrated in Table 10.1, where two states, ω1 and ω3, result in the same cash flow, x1. Formally, this may be expressed as
Table 10.1: Exemplary mapping from ![]() to
to ![]() at date t > 0
at date t > 0
| State |
Cash flow |
|
|---|---|---|
| ω1 | → | x1 |
| ω2 | → | x2 |
| ω3 | → | x1 |
10.5.3 Contingent Claims and State Prices
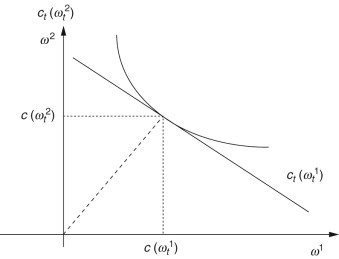
From the point of view of the investor, the realisation of different states of nature does not have the same value, and hence the monetary unit resulting from the corresponding claims are not of equal subjective value. How is that?
The usefulness of a good often depends on the circumstances (or “state of nature”) in which it becomes available: An umbrella when it is raining has a different appeal than an umbrella when it is not raining. Another example is the amount of ice cream that can be consumed in hot weather and cold weather. Although the actual ice cream will cost the same, the utility drawn from its consumption is most likely much higher in hot than in cold weather. A more serious example involves health insurance: How much would a million Euros be worth to someone lying in a coma?
As the investor is interested primarily in the utility drawn from consumption levels, it is important to distinguish levels of consumption by the state of nature in which they may be consumed.
This difference in utility is captured by the state price concept, q0(ωt), measuring the value the investor attributes to receiving a unit monetary value in a specific state ωt. It is also the price at date t = 0 of a contingent claim (Arrow-Debreu security), and hence also is called contingent claim price.
With this concept in mind, we can decompose assets promising an uncertain future cash flow ![]() into Ω elementary securities, each consisting of x(ωt) Arrow-Debreu securities
into Ω elementary securities, each consisting of x(ωt) Arrow-Debreu securities ![]() . Every such elementary security represents the cash flow received in a specific state and, as utility differs for each state, is separately priced. To see how this works, consider the example in Table 10.2.
. Every such elementary security represents the cash flow received in a specific state and, as utility differs for each state, is separately priced. To see how this works, consider the example in Table 10.2.
Table 10.2: States of nature and corresponding cash flows
| State Description | State at date t | Cash flow at date t |
|---|---|---|
| Bad weather | ω1 | x1 = 100 EUR |
| Good weather | ω2 | x2 = 5 EUR |
In this example, there are two states of nature, Ω = {ω1, ω2}, and two possible cash flow values Xt = {x1, x2} = {100, 5} that are contingent according the mapping set out in Table 10.2. As each Arrow-Debreu security yields exactly one Euro in the corresponding state of nature, the value for the investor of receiving the 100 Euros in bad weather is
and the value of receiving the five Euros in good weather is
xt(ω) denotes the asset’s cash flow in state of nature ![]() . Using q0(ω) and xt(ω) the decomposition of the asset into a bundle of orthogonal16 contingent claims, each potentially resulting in a different cash flow, the asset’s price must then equal the value of the contingent claims of which it is a bundle,
. Using q0(ω) and xt(ω) the decomposition of the asset into a bundle of orthogonal16 contingent claims, each potentially resulting in a different cash flow, the asset’s price must then equal the value of the contingent claims of which it is a bundle,
10.5.4 Investor Decision under Uncertainty
How should we interpret the notion of a state price and the pricing formula, Equation (10-14), and how is this related to the Central Pricing Equation? Why is one state preferred over another and hence given a higher value by the investor? To find this out, we again take a look at the decision problem of an individual in the consumption-based context, this time explicitly modelling the uncertainty across various states of nature.
From the contingent claim framework we now have an explicit formulation of the future consumption level, ![]() , as a function of the state of nature. Start with transforming the budget constraint for the future consumption level by using the mapping from
, as a function of the state of nature. Start with transforming the budget constraint for the future consumption level by using the mapping from ![]() to
to ![]() ,
, ![]() .
.
Next, we adjust the utility function to account for uncertainty in a more explicit way. Denote ![]() as the probability as perceived by the investor at date t = 0 that state ω will emerge (i.e.,
as the probability as perceived by the investor at date t = 0 that state ω will emerge (i.e., ![]() ) at date t. The probabilities π0(ω)are the investors’ subjective probabilities for the various states. Asset prices are set, after all, by investors’ demands for assets, and those demands are set by investors’ subjective evaluations of the probabilities of various events. Using Equation (10-15) we can formulate the expectation of the future utility as
) at date t. The probabilities π0(ω)are the investors’ subjective probabilities for the various states. Asset prices are set, after all, by investors’ demands for assets, and those demands are set by investors’ subjective evaluations of the probabilities of various events. Using Equation (10-15) we can formulate the expectation of the future utility as
The investor’s decision problem may then be written as
Note that we have proper probabilities for the various state of the lottery and this expectation shows how Equation (10-6) satisfies the expected utility criterion needed for working with additive utility functions in the context of uncertainty.
As in Chapter 4, we insert the restrictions into the objective function to get
The first-order condition for an optimum of this is:17
which is nothing else than a more detailed formulation of the Central Pricing Equation ![]() for the case that the uncertainty surrounding
for the case that the uncertainty surrounding ![]() is described by the state of nature random variable
is described by the state of nature random variable ![]() .
.
Further differentiating Equation (10-16) with respect to xt(ω) provides—in analogy to Equation (10-14)—a structural expression linking the state price q0(ω) to the marginal utility of the investor:
This illustrates how the state price measures the value of the emergence of a state (and resulting cash flow) for the investor in terms of utility. It also brings along the interpretation of the stochastic discount factor ![]() as a set of contingent claim prices, scaled by probabilities. As a result of this interpretation, the combination of discount factor and probability is sometimes called state-price density:
as a set of contingent claim prices, scaled by probabilities. As a result of this interpretation, the combination of discount factor and probability is sometimes called state-price density:
This formulation also shows that the randomness in the discount factor comes from the uncertainty about the future state of nature.
Assuming smooth utility functions, the same logic as in Section 10.4 ensures that state prices q0(ωt) are proportional to each investor’s marginal rate of substitution between current and future consumption, that is
The investor’s first-order conditions say that the marginal rate of substitution between states at date t equals the relevant price ratio for the case that π0(ω1) = π0(ω2),
m(ω1)/m(ω2) gives the rate at which the investor can give up consumption in state 2 in return for consumption in state 1 through purchase and sales of contingent claims.
We learn that the discount factor m is the marginal rate of substitution between date—and state—contingent commodities. That is why it, like c(ω), is a random variable.
Figure 10.7 gives the economics behind this approach to asset pricing. The investor’s first-order conditions in a contingent claims market implies that the marginal rate of substitution equals the discount factor and the contingent claim price ratio.
10.5.5 Special Case I: The Risk-free Rate
An important concept to which we will have much recourse is the risk-free rate, which we can now define and characterise.
Think of an instrument that generates the same cash flow whatever the state of nature; that is, where ![]() . We call this instrument the risk-free instrument and the return it generates, the risk-free rate.
. We call this instrument the risk-free instrument and the return it generates, the risk-free rate.
The risk-free rate is the ratio of future cash flow to current price, ![]() , for an instrument that guarantees (by all means of probability) the same cash flow in all possible states Ω; that is,
, for an instrument that guarantees (by all means of probability) the same cash flow in all possible states Ω; that is,
Accordingly, ![]() is called the net risk-free rate from date 0 to date t and
is called the net risk-free rate from date 0 to date t and ![]() stands for the corresponding gross risk-free rate.
stands for the corresponding gross risk-free rate.
10.5.6 Special Case II: Equivalent Martingale Measures
Another important concept that is fundamental for derivative pricing is the equivalent martingale measures. A martingale is a stochastic process ![]() such that at any date t = 0 its conditional expectation for date t > 0 coincides with its current value:
such that at any date t = 0 its conditional expectation for date t > 0 coincides with its current value: ![]() . In discrete time (i.e., when time is measured by separable dates), a martingale is a process the value of which at any date is equal to its conditional expectation for one date later.
. In discrete time (i.e., when time is measured by separable dates), a martingale is a process the value of which at any date is equal to its conditional expectation for one date later.
Price processes, pt, are in general not martingales, meaning that empirically they usually exhibit a drift or trend. If we recognise that prices are equal to the discounted values of expected future cash flows, it can be demonstrated that in the absence of arbitrage there is a probability measure in which all price processes, appropriately discounted, become martingales. The law of iterated expectation then implies that price plus payoff processes are martingales.
To illustrate this, assume a continuity of dates starting with t = 0, that is, t = {0, 1, 2, 3, …, T}. If we use the risk-free rate from date 0 to t, ![]() , to discount future cash flows, we may formulate the Central Pricing Equation as
, to discount future cash flows, we may formulate the Central Pricing Equation as
Note that this formulation presupposes the absence of arbitrage, a market-price generating concept that implies that the correct discount factor for market prices is the risk-free rate. We use this concept repeatedly in this book.
It is also important to note that this approach deviates from the consumption-based theory as it takes away the investor-specific inter-temporal preferences in its quest for statistically convenient, “investor-neutral” valuation approach. This has important consequences, when interpreting valuations that are done using the equivalent martingale measure approach.
Acknowledge further that the series of cash flows generated by the instrument is
With the definition of the uncertain future cash flow at date t, ![]() , we can write the price of the instrument being discounted by risk-free rates as
, we can write the price of the instrument being discounted by risk-free rates as
From this formulation we know that
which, using risk free rates, is equivalent to
implying, in turn, nothing else than ![]() . Equation (10-18) shows that the discounted price plus income process is a martingale. The terms on the left are the price processes, the terms on the right are the conditional expectations under the probability measure Q of the expected cash flows discounted with the risk-free rate (cash flow).
. Equation (10-18) shows that the discounted price plus income process is a martingale. The terms on the left are the price processes, the terms on the right are the conditional expectations under the probability measure Q of the expected cash flows discounted with the risk-free rate (cash flow).
It is important to realise that, with equivalent martingale measures, we deviate from the pure Central Pricing Equation that acknowledges investor-specific discount factors and preferences. From a “true price” perspective, using ![]() would be justified only if there is no risk inherent to xt (i.e.,
would be justified only if there is no risk inherent to xt (i.e., ![]() ), which is only true for very few instruments.
), which is only true for very few instruments.
It is the absence of arbitrage principle that forces market prices to be consistent with Equation (10-18). Always keep in mind, however, that this price may not be the best one reflecting your own economic situation and preferences, but rather the one that you might expect to see in the markets as an equilibrium outcome.
The equivalent martingale measure EQ[] is a mathematical construct. It illustrates that the concept of arbitrage depends only on the structure of the price and payoff processes and not on the actual probabilities. As we will see later, equivalent martingale measures simplify the computation of the pricing of derivatives in important ways.
The term “equivalent probability measure” comes from the statistical theory: Given a probability measure P the probability measure Q is said to be equivalent to P if both assign probability zero to the same events. An equivalent probability measure Q is an equivalent martingale measure if all price processes discounted will become martingales. More precisely, Q is an equivalent martingale measure if and only if the market value of any trading strategy is a martingale.
10.5.7 Special Case III: Risk-neutral Probabilities
The concept of equivalent martingale measure requires that the stochastic discount factor ![]() is equal to the risk-free rate
is equal to the risk-free rate ![]() . In this section we will have a closer look at this and the conditions under which this makes sense.
. In this section we will have a closer look at this and the conditions under which this makes sense.
With the risk-free rate, the discount factor is state independent. It is common to assume that ![]() , that the subjective discount factor of the risk-neutral investor is equal to the risk-free rate.
, that the subjective discount factor of the risk-neutral investor is equal to the risk-free rate.
Much of the difficulty in interpreting the Central Pricing Equation lies in the (unknown degree of) risk aversion of individual investors over time and between states of nature. How would the central pricing equation look if investors were not risk-averse?
Recall the definition of the state dependent discount factor from Section 10.5.4:
From the discussion of utility functions in Section 10.4.2 we know that if investors are risk-neutral, the first derivative of their utility function is constant for all consumption levels; that is, u′(c0) = u′(ct(ω)) ∀ω. As a consequence, u′(c0)/u′(ct(ω)) = 1 ∀ω and the discount factor becomes state-independent, equal to the subjective discount factor of a risk-neutral investor, independent of consumption levels:
Another useful relationship may be found if we take the right two expressions and rearrange them to have q0(ω) = π(ω)β. As ![]() and, by its definition as a probability function
and, by its definition as a probability function ![]() we have
we have
Consequently, with risk-neutral investors, the expected value of the discount factor is unique across all states and itself equal to the sum of state prices.
For the case of risk-neutral investors, we denote the discount factor as ![]() and the risk-neutral probability as
and the risk-neutral probability as ![]() . Using this and expanding it we find the definition of the risk-neutral probability in terms of discount factors
. Using this and expanding it we find the definition of the risk-neutral probability in terms of discount factors
![]() are positive, less than or equal to one, and sum to one, so they are a legitimate set of probabilities. Using
are positive, less than or equal to one, and sum to one, so they are a legitimate set of probabilities. Using ![]() and
and ![]() , assuming a risk-free asset, we can rewrite the asset pricing formula for risk-neutral investors as
, assuming a risk-free asset, we can rewrite the asset pricing formula for risk-neutral investors as
which is the formulation we need to justify the equivalent martingale measure in the previous section; that is, ![]() .
. ![]() denotes the conditional expectation with respect to the modified probability distribution.
denotes the conditional expectation with respect to the modified probability distribution.
The assumption of risk neutrality of the investor allows eliminating the utility function from the stochastic discount factor. As a consequence, the probabilities ![]() differ from the subjective probabilities π0(ω) in that they are not dependent on a utility function, which is equivalent to assuming that the investor(s) is risk-neutral, hence the name risk-neutral probabilities. They are not, in general, the real probabilities associated with states by individual investors.
differ from the subjective probabilities π0(ω) in that they are not dependent on a utility function, which is equivalent to assuming that the investor(s) is risk-neutral, hence the name risk-neutral probabilities. They are not, in general, the real probabilities associated with states by individual investors.
The use of risk-neutral probabilities has a very fundamental interpretation: risk aversion is equivalent to paying more attention to unpleasant states, relative to their actual probability of occurrence. People who report high subjective probabilities of unpleasant events may not have irrational expectations, but simply may be reporting the risk-neutral probabilities or the product q0(ω) = π0(ω)m0,t(ω). This product is, after all, the most important piece of information for many decisions: pay a lot of attention to contingencies that are either highly probable or that are improbable but have disastrous consequences!
Bringing back the discount factor and inserting q0(ω) = π0(ω)m0,t(ω) and ![]() into the definition of the risk-neutral probability (…) we obtain the transformation from actual (i.e., risk-averse) to risk-neutral probabilities:
into the definition of the risk-neutral probability (…) we obtain the transformation from actual (i.e., risk-averse) to risk-neutral probabilities:
We can also think of the discount factor m as the derivative or change of measure from the real probabilities π to the subjective probabilities π*. The risk-neutral probability representation of asset pricing is quite common, especially in derivative pricing where the results are often independent of risk adjustments.
If ![]() then we can write the two-dates Central Pricing Equation as
then we can write the two-dates Central Pricing Equation as
1See Cochrane (2005), for a very good introduction and overview to this theory, its shortcomings as well as the relevant literature references to this subject.
2We will see later that once the single cash flow problem is solved properly, the extension to a multicash flow situation is a straightforward exercise, so this assumption does not limit the validity of our considerations.
3For a detailed exposition of asset pricing theory, see Cochrane (2005), Duffie (2001), Huang and Litzenberger (1988), Ingersoll (1987).
4For example, this setting applies for any type of investment where there is only one expected future payoff, such as a zero coupon bond, a closed fund investment, an index certificate, or a floating rate note/bond, where only the next expected coupon payment is considered.
5See Chiang and Wainwright (2005) for an in-depth and easy-to-understand discussion of the algebra of utility functions.
6See Varian (2006) for an intuitive explanation of the surrounding axioms, or—more advanced but having a benchmark character—Mas-Colell et al. (1995).
7An individual may also be risk-loving; in such a case, the consumer prefers a lottery to its expected value.
8v(u(c)) = 2u(c) → ![]() , which is larger than
, which is larger than ![]() .
.
9There exists a large branch of financial economics that tries to explicitly specify a functional form for a “typical” utility function. Besides the fact that such an honourable endeavour is of little relevance for our purposes, they usually are confronted with the full arsenal of practical complications, like validity of representativeness assumption, non-availability of appropriate micro-data, just to name a few. What is important for us is that you take the theory as a tool to structure your thinking about prices of (financial) assets, but nothing more.
10The optimality condition implies the first derivative of U( ) with respect to n being equal to 0. Inserting the restrictions (10-3) and (10-4) into U( ) yields:
Taking the first derivative with respect to n and equalling it to zero produces
The second condition for a maximum is that the second derivative of the objective function with respect to n is negative over all values of c, i.e.,
As ![]() , this is by definition smaller than zero.
, this is by definition smaller than zero.
11To see this, let v(u) be a monotonic transformation of utility. The marginal rate of substitution for this utility function is
The fraction on the left is the marginal rate of substitution between good i and j, and the fraction on the right might be called the economic rate of substitution between goods i and j. Maximization implies that those two rates of substitution be equal.
12An example for such a cash flow stream might be a fixed coupon bond, where we have a number of income (coupon) payments and, at date T, the redemption price, plus possibly a final income payment:
Note that periods between the dates do not need to be equidistant for the approach to hold.
13Both Arrow and Debreu are later awarded the Nobel Prize in Economics for their contribution in this very field.
14See Arrow (1964); more developed, Nagatani (1975); and for a summary, Radner (1982).
15As shown in Section 10.2.2, the proper definition of possible states, in particular their mutual exclusiveness, is key to having a meaningful definition of a random variable.
16Orthogonality is equivalent in this case to mutual exclusiveness and comes from the requirement that the states of nature in Ω are mutually exclusive, so if one state emerges no other state can emerge as well. If a claim is realized (i.e., a particular state of nature has emerged in date t), then all other contingent claims not corresponding to this state of nature are void as no two or more contingent claims can materialise at the same time.
17The second order condition is
as u″( ) < 0, this expression becomes < 0.