Appendix 1

Jule’s Solution

Below, we give some hints for the solution of the probability question posted on canyousolveit.com (p. 6). The concepts, formulas, and notation used should be familiar to an undergraduate student in mathematics.

We consider the general case of n players. A distribution of n hats among these n players is represented mathematically as a permutation s on a set {1, 2, . . . , n} of n elements, where s(i) = j means that player i picks hat j. The number of these permutations is n!

Those permutations s for which s(i) ≠ i for i = 1, 2, . . . , n, are called derangements, and they correspond to distributions of hats for which none of the players picks his own hat.

Then, the probability that none of the n players will pick his own hat is d/n! where d is the number of derangements.

To find the value of d, let P denote the set of all permutations and D the set of derangements (on n elements).

P can be expressed as the union of D and subsets F_i, i = 1, 2, . . . , n, of P where F_i is the set of permutations s that leave i fixed, that is, such that s(i) = i. In symbols,

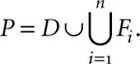
From the equation above it follows that n! = d + f, where f is the number of permutations in the union of the F_i.

The collection F₁, F₂, . . . , F_n of subsets of P has the following property:

The number of elements in the intersection of any k subsets in the collection depends only on k and it is given by (n−k)!

Applying the so-called Inclusion-Exclusion Principle to the F_i we get the formula

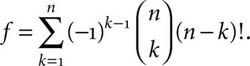
Finally, it is straightforward to obtain

d/n! = 1/2! − 1/3! + 1/4! − 1/5!+ . . . ±1/n!

which gives the desired probability.

For n = 12, this probability is approximately 0.3679.

The limit of d/n! as n tends to infinity is the sum of the infinite series representation of e^x for x = −1, or 1/e.