Hour 2. Game Objects
What You’ll Learn in This Hour:
► How to work with 2D and 3D coordinates
► How to work with game objects
► How to work with transforms
Game objects are the foundational components of a Unity game project. Every item that exists in a scene is, or is based on, a game object. In this hour, you’ll learn about game objects in Unity. Before you can start working with objects in Unity, however, you must learn about the 2D and 3D coordinate systems. After you learn about those systems in this hour, you will begin working with the built-in Unity game objects, and you will wrap up the hour by learning about the various game object transformations. Information gained in this hour is foundational to everything else in this book. Be sure to take your time and learn it well.
Dimensions and Coordinate Systems
For all their glitz and glamour, video games are mathematical constructs. All the properties, movements, and interactions can be boiled down to numbers. Luckily for you, a lot of the groundwork has already been laid. Mathematicians have been toiling away for centuries to discover, invent, and simplify different processes, and all their work means you can more easily build games with modern software. You may think the objects in a game just exist in space randomly, but really every game space has dimensions, and every object is placed in a coordinate system (or grid).
Putting the D in 3D
As mentioned previously, every game uses some level of dimensions. The most common dimension systems, the ones you are most likely familiar with, are 2D and 3D (short for two-dimensional and three-dimensional). A 2D system is a flat system. In a 2D system, you deal only with vertical and horizontal elements (or, to put it another way: up, down, left, and right).
Games like Tetris, Pong, and Pac Man are good examples of 2D games. A 3D system is like a 2D system, but it obviously has one more dimension. In a 3D system, you have not only horizontal and vertical (up, down, left, and right) but also depth (in and out). Figure 2.1 does a good job of illustrating the differences between a 2D square and a 3D square, otherwise known as a cube. Notice how the inclusion of the depth axis in the 3D cube makes it seem to “pop out.”
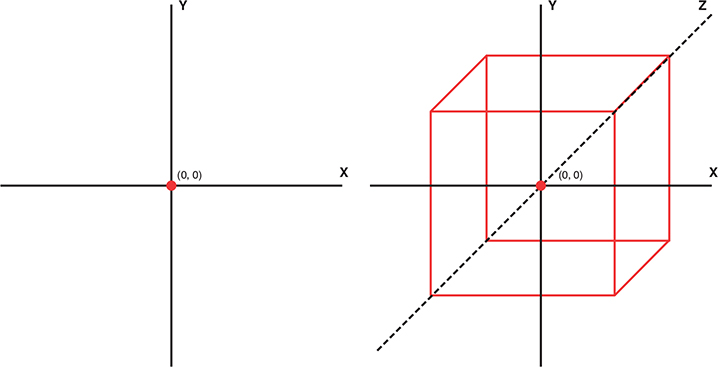
FIGURE 2.1
2D square versus 3D cube.
Using Coordinate Systems
The mathematical equivalent of a dimension system is a coordinate system. A coordinate system uses a series of lines, called axes (the plural of axis), and locations, called points. These axes correspond directly with the dimensions they mimic. For instance, a 2D coordinate system has the x axis and y axis, which represent the horizontal and vertical directions, respectively. If an object is moving horizontally, we say it is moving “along the x axis.” Likewise, the 3D coordinate system uses the x axis, the y axis, and the z axis for horizontal, vertical, and depth movement and positioning, respectively.
World Versus Local Coordinates
You have now learned about the dimensions of a game world and about the coordinate systems that compose them. What you have been working with so far is considered the world coordinate system. At any given time, there is only a single x axis, a single y axis, and a single z axis in the world coordinate system. Likewise, there is only one origin that all objects share. What you might not know is that there is also something called the local coordinate system. This system is unique to each object, and it is completely separate from the local coordinate systems of other objects. This local system has its own axes and origin that other objects don’t use. Figure 2.3 illustrates the world versus local coordinate systems by showing the four points that make up a square for each.
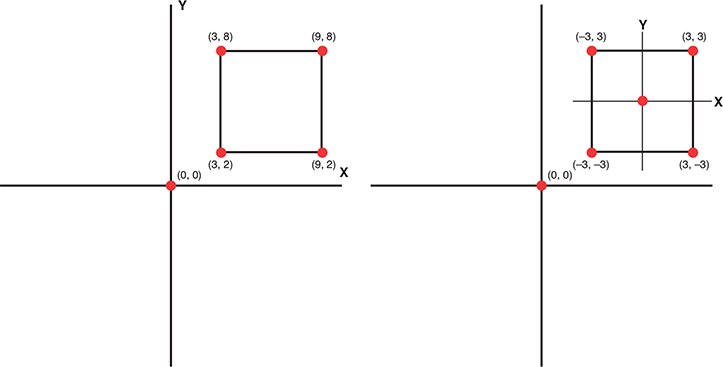
FIGURE 2.3
World coordinates (left) versus local coordinates (right).
You might be wondering what the local coordinate system is for if the world coordinate system is used for the positions of objects. Later in this hour, you will look at transforming game objects and at parenting game objects. Both of these require the local coordinate system.
Game Objects
All shapes, models, lights, cameras, particle systems, and so on in a Unity game have one thing in common: They are all game objects. The game object is the fundamental unit of any scene. Even though they are simple, game objects are very powerful. At their root, game objects are little more than transforms (discussed in greater detail later in the hour) and containers. The container part of a game object exists to hold the various components that make the object more dynamic and meaningful. What you add to your game objects is up to you. There are many components, and they add a huge amount of variety. Throughout the course of this book, you will be learning to use many of these components.
Transforms
So far in this hour, you have learned and explored the different coordinate systems and experimented with some game objects. It is time to put the two together. When dealing with 3D objects, you often hear the term transform. Depending on the context, transform is either a noun or a verb. All objects in 3D space have a position, a rotation, and a scale. If you combine them, you get an object’s transform (noun). Alternatively, transform can be a verb if it refers to changing an object’s position, rotation, or scale. Unity combines the two meanings of the word with the transform component.
Recall that the transform component is the only component that every game object has to have. Even empty game objects have transforms. Using this component, you can both see the current transform of the object and change (or transform) the transform of the object. It might sound confusing now, but it is fairly simple. You will get the hang of it in no time. Because the transform is made up of the position, rotation, and scale, it stands to reason that there are three separate methods (called transformations) of changing the transform: translation, rotation, and scaling. These transformations can be achieved using either the Inspector or the transform tools. Figures 2.4 and 2.5 illustrate which Inspector components and tools correlate with the various transforms.
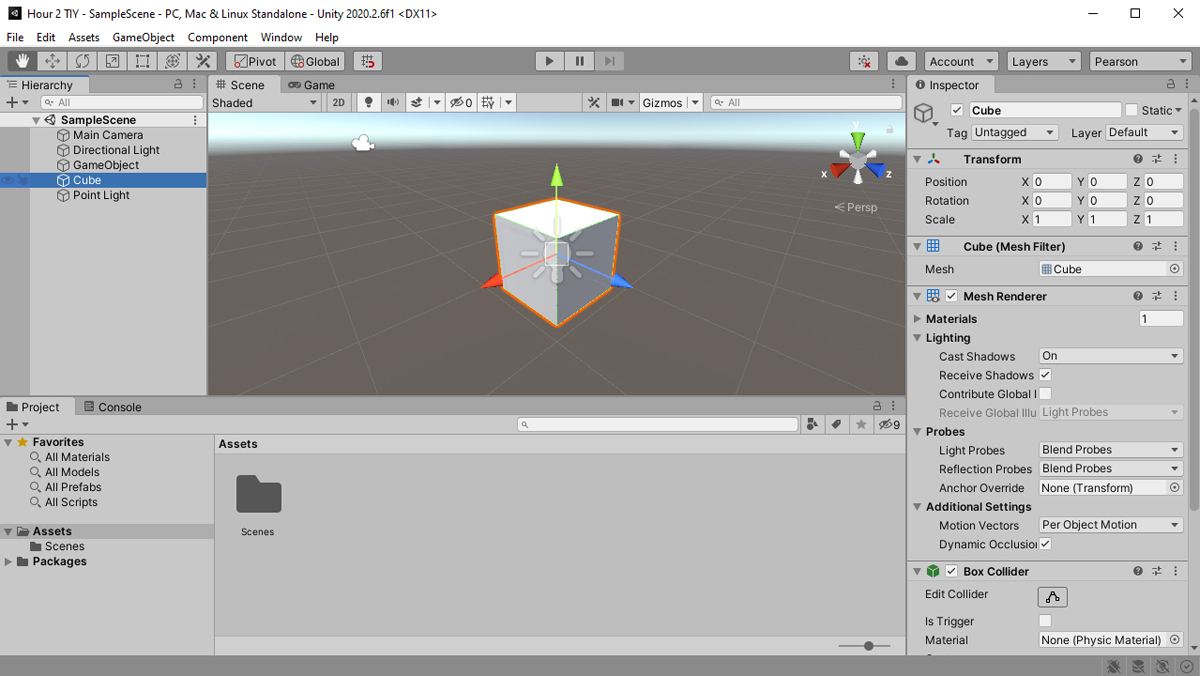
FIGURE 2.4
Transform options in the Inspector.

FIGURE 2.5
The transform tools.
Translation
The process of changing the coordinate position of an object in a 3D system is called translation, and it is the simplest transform you can apply to an object. When you translate an object, it is shifted along an axis. Figure 2.6 demonstrates a square being translated along the x axis.
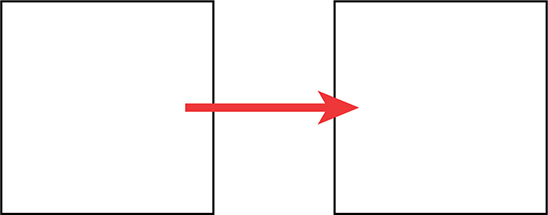
FIGURE 2.6
Sample translation.
When you select the Translate tool (hotkey: W), whatever object you have selected changes slightly in the Scene view. More specifically, you see three arrows appear, pointing away from the center of the object along the three axes. These are translation gizmos, and they help you move your objects around in the scene. Clicking on and holding any of these axis arrows causes them to turn yellow. Then, if you move your mouse, the object moves along that axis. Figure 2.7 shows what the translation gizmos look like. Note that the gizmos appear only in the Scene view.

FIGURE 2.7
Translation gizmos.
Rotation
Rotating an object does not move it in space. Instead, it changes the object’s relationship to that space. More simply stated, rotation enables you to redefine which directions the x, y, and z axes point for a particular object. When an object rotates around an axis, it is said to be rotating about that axis. Figure 2.8 shows a square being rotated about the z axis.
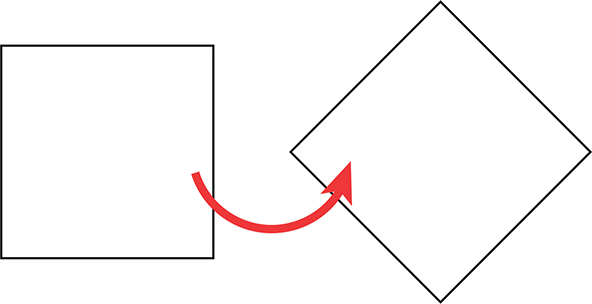
FIGURE 2.8
Rotation about the z axis.
Scaling
Scaling causes an object to grow or shrink within a 3D space. This transform is really straightforward and simple to use. Scaling an object on any axis causes its size to change on that axis. Figure 2.10 demonstrates a square being scaled down on the x and y axes. Figure 2.11 shows what the scaling gizmos look like when you select the Scaling tool (hotkey: R).

FIGURE 2.10
Scaling on the x and y axes.

FIGURE 2.11
The scaling gizmos.
Hazards of Transformations
As mentioned earlier in this hour, transformations use the local coordinate system. Therefore, the changes that are made can potentially impact future transformations. For example, in Figure 2.12, notice how the same two transformations, when applied in reverse order, have very different effects.

FIGURE 2.12
Effects of transformation order.
As you can see, not paying attention to transformation order can have unexpected consequences. Luckily, the transformations have consistent effects that can be planned on:
► Translation: Translation is a fairly inert transformation. This means that any changes applied after it generally are not affected.
► Rotation: Rotation changes the orientation of the local coordinate system axes. Any translations applied after a rotation cause the object to move along the new axes. If you were to rotate an object 180 degrees about the z axis, for example, and then move in the positive y direction, the object would appear to be moving down instead of up.
► Scaling: Scaling effectively changes the size of the local coordinate grid. Basically, when you scale an object to be larger, you are really scaling the local coordinate system to be larger. This causes the object to seem to grow. This change is multiplicative. For example, if an object is scaled to 1 (its natural, default size) and then translated 5 units along the x axis, the object appears to move 5 units to the right. If the same object were to be scaled to 2, however, then translating 5 units on the x axis would result in the object appearing to move 10 units to the right. This is because the local coordinate system is now double the size, and 5 times 2 equals 10. Inversely, if the object were scaled to .5 and then moved, it would appear to move only 2.5 units (.5 × 5 = 2.5).
Once you understand these rules, determining how an object will change with a set of transformations is easy. These effects depend on whether you have Local or Global selected, and they take some getting used to, so it is a good idea to experiment.
Gizmo Positions
The gizmo placement options can be very confusing for a new user who doesn’t know what they do. Effectively, these options control the position and alignment of the transform gizmos in the scene view. Check out Figure 2.13 to see how the alignment of the translate gizmos changes depending on whether you have the option set to Local or Global coordinate space.
In addition, see Figure 2.14 to learn how the placement of the gizmos changes when you have multiple objects selected. With the Pivot option selected, the gizmos function centers on the first object selected. With the Center option selected, the gizmos are placed and function in the center of all of the selected objects.
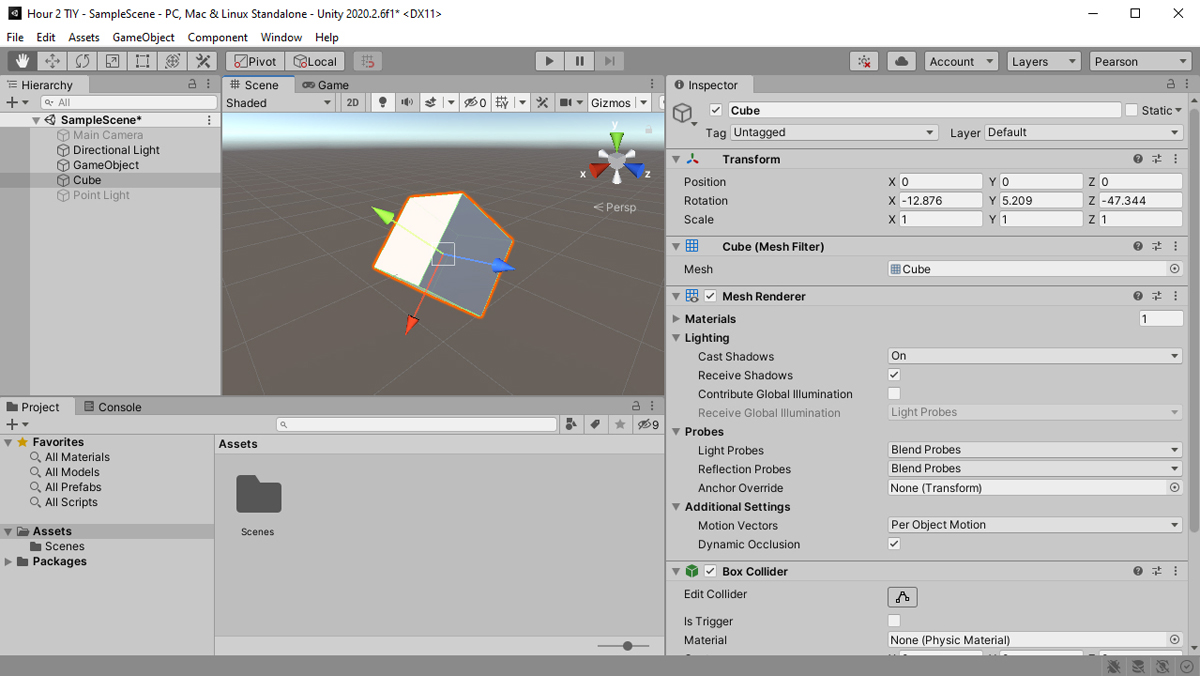
FIGURE 2.13
The alignment of the gizmos for Local versus Global.


FIGURE 2.14
The position of the gizmos for Pivot versus Center.
Generally speaking, you should keep your gizmos set to Pivot and Local to avoid confusion and to make your day-to-day work in Unity easier.
Transforms and Nested Objects
In Hour 1, “Introduction to Unity,” you learned how to nest game objects in the Hierarchy view (by dragging one object onto another one). Recall that when you have an object nested inside another one, the top-level object is the parent, and the other object is the child. Transformations applied to the parent object work as normal. The object can be moved, scaled, and rotated. What’s special is how the child object behaves. Once nested, a child object’s transform is relative to that of the parent object—not relative to the world. Therefore, a child object’s position is not based on its distance from the origin but the distance from the parent object. If the parent object is rotated, the child object moves with it. If you looked at the child’s rotation, however, it would not register that it had rotated at all. The same goes for scaling. If you scale the parent object, the child also changes in size. The scale of the child object remains unchanged. You might be confused by this. Remember that when a transformation is applied, it is not applied to the object but to the object’s coordinate system. An object isn’t rotated; its coordinate system is rotated. The effect is that the object seems to turn. When a child object’s coordinate system is based on the local coordinate system of the parent, any changes to the parent system directly change the child (without the child knowing about it).
Summary
In this hour, you have learned all about game objects in Unity. You started off by learning all about the differences between 2D and 3D. From there, you looked at the coordinate system and how it breaks down the “world” concepts mathematically. You then began working with game objects, including some of the built-in ones. You ended by learning about transforms and the three transformations. You got to try out the transforms, learn about some of the hazards, and see how transforms affect nested objects.
Q&A
Q. Is it important to learn both the 2D and the 3D concepts?
A. Yes. Even games that are entirely 3D still use some of the 2D concepts on a technical level.
Q. Should I learn to use all the built-in game objects right away?
A. Not necessarily. There are many game objects, and it can be overwhelming to attempt to learn them all right away. Take your time and learn about the objects as they are covered here.
Q. What is the best way to get familiar with transforms?
A. Practice. Keep working with them; eventually, they will become quite natural.
Workshop
Take some time to work through the questions here to ensure that you have a firm grasp of the material.
Quiz
1. What does the D in 2D and 3D stand for?
2. How many transformations are there?
3. True or False: Unity has no built-in objects, and you must create your own.
4. Say you have an object at (0, 0, 0). What is its new position if you move it 1 unit on the x axis and then rotate it 90 degrees about the z axis? What if, instead, you rotated it before moving it?
Answers
1. Dimension
2. Three
3. False. Unity provides many built-in objects.
4. Moving and then rotating results in a position of (1, 0, 0). Rotating and then moving results in a position of (0, 1, 0). If this is confusing to you, be sure to revisit the section “Hazards of Transformations” in this hour.
Exercise
Take a moment to experiment with the way transformations work in a parent/child object scenario. You will get a better feel for exactly how the coordinate systems change the way things are oriented.
1. Create a new scene or a project.
2. Add a cube to the scene and place it at (0, 2, –5). Remember the shorthand notation for coordinates: The cube you add should have an x value of 0, a y value of 2, and a z value of –5. You can set these values easily in the transform component in the Inspector view.
3. Add a sphere to your scene. Pay attention to the sphere’s x, y, and z values.
4. Nest the sphere under the cube by dragging the sphere onto the cube in the Hierarchy view. Notice how the position values changed. The sphere is now located relative to the cube.
5. Place the sphere at (0, 1, 0). Notice how it doesn’t go to right above the origin and instead sits right above the cube.
6. Experiment with the various transformations. Be sure to try them on the cube as well as the sphere and see how differently they behave for a parent than for a child object.