Basic Material 417
In the noncompact case, there are isomorphisms b etween the corresponding dual
spaces.
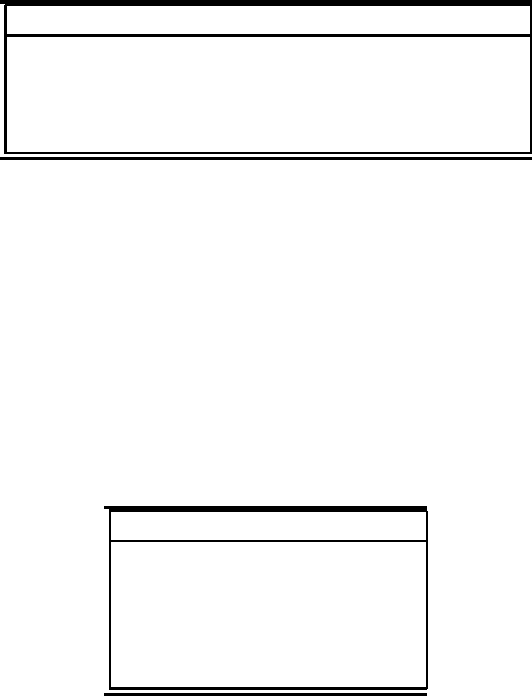
TABLE A.4: Exceptional symmetric spaces of types II and IV
Type I (compact) Type III (noncompact) Dimension Rank
E
6
E
6
(C)/E
6
78 6
E
7
E
7
C)/E
7
133 7
E
8
E
8
(C)/E
8
248 8
F
4
F
4
(C)/F
4
52 4
G
2
G
2
(C)/G
2
14 2
Hermitian symmetric spaces
A Hermitian symmetric space is a Riemannian symmetric space that is equipped
with a K¨ahler structure so that the geodesic symmetries are holomorphic maps. The
simplest example of a Hermitian symmetric space is the complex vector space C
n
.
For semisimple Riemannian symmetric spaces one can easily decide whether it is
Hermitian or not. In fact, let (G,K) be the Riemannian symmetric pair of an irre-
ducible Riemannian semisimple symmetric space M. Then the center of K is ei-
ther discrete or one-dimensiona l. The irreducible semisimple Hermitian symmetr ic
spaces are precisely those for which the center of K is one-dimensional. This gives
the list in Table A.5
TABLE A.5: Irreducible Hermitian symmetric spaces
Compact Type Noncompact Type
SU
p+q
/S(U
p
U
q
) SU
p,q
/S(U
p
U
q
)
SO
2+q
/SO
2
SO
q
SO
o
2,q
/SO
2
SO
q
SO
2n
/U
n
SO
∗
2n
/U
n
Sp
n
/U
n
Sp
n
(R)/U
n
E
6
/Spin
10
U
1
E
−14
6
/Spin
10
U
1
E
7
/E
6
U
1
E
−25
7
/E
6
U
1
Note that SO
4
/SO
2
SO
2
is isometric to the Riemannian product S
2
×S
2
and there-
fore we have to exclude the case q = 2 in the second row of the above table. Every
semisimple Hermitian symmetric space is simply connected and hence decomposes
into the Riemannian product of irreducible Hermitian symmetric spaces.
Complex flag manifolds
Let G be a connected compact real semisimple Lie group with trivial center and
g its Lie algebra. Co nsider the action o f G on g by the adjoint representation Ad :
G → End(g). For each 0 = X ∈ g the orbit
G ·X = {Ad(g)X : g ∈ G}
418 Submanifolds and Holonomy
is a homogeneous G-space. Let t
X
be the intersection of all maximal abelian subal-
gebras of g containing X and T
X
the torus in G with Lie algebr a t
X
. Then the isotropy
subgroup of G at X is Z
G
(T
X
), the centralizer of T
X
in G, and therefore
G ·X = G/Z
G
(T
X
).
In particular, if X is a regular element of g, that is, if there is a unique maximal
abelian subalgebra t of g containing X,thenG ·X = G/T ,whereT is the maximal
torus in G with Lie algebra t. Any orbit G ·X of the adjoint representation of G is
called a complex flag manifold or C-space. The latter notion is used mor e frequently
in earlier papers on this topic. In the special case of G = SU
n
one obtains the flag
manifolds of all possible flags in C
n
in this way. In particular, when T is a maximal
torus of SU
n
,thenSU
n
/T is the flag manifold of all full flags in C
n
, that is, of all
possible arrangements {0}⊂V
1
⊂ ... ⊂ V
n−1
⊂ C
n
,whereV
k
is a k-dimensional
complex linear subspace of C
n
.
The importance of complex flag manifolds becomes clear from the following
facts. Each orbit G ·X admits a canonical complex structure, which is also integrable.
If G is simple, there exists a unique (up to homothety) G-invariant K¨ahler-Einstein
metric on G ·X with positive scalar curvature and compatible with the canonical com-
plex structure on G ·X. Moreover, any K¨ahler-Einstein metric on G ·X is homoge-
neous under its own group of isometries and is obtained from a G-invariant K¨ahler-
Einstein metric via some automorphism of the complex structure. Conversely, any
simply connected, compact, homogeneous K¨ahler manifold is isomorphic as a com-
plex homogeneous manifold to some orbit G ·X of the adjoint representation of G,
where G = I
o
(M) and X ∈g. Note that each compact homogeneous K¨ahler manifold
is the Riemannian product of a flat complex torus and a simply connected, compact,
homogeneous K¨ahler manifold.
Real flag manifolds
A real flag manifold is an orbit of an s-representation. Real flag manifolds are
also known as R-spaces, a terminology that is used more f requently in earlier papers
on this topic. Note that the s-representation of a Riemannian symmetric space of
noncompact type is the same as the one of the corresponding dual symmetric space.
Thus, in order to classify and study real flag manifolds, it is sufficient to consider just
one type of symmetric spaces.
Let M = G/K be a semisimple Riemannian symmetric space of noncompact type
with G = I
o
(M), o ∈ M and K the isotropy group of G at o. Note that K is connected
as M is simply connected and G is connected. We consider the corresponding Cartan
decomposition g = k ⊕p of the real semisimple Lie algebra g.Let0= X ∈ p and
K ·X the orbit of K through X via the s-representation. For each k ∈ K we have
k ·X = d
o
k(X)=Ad(k)X and therefore
K ·X = K/K
X
with K
X
= {k ∈K : Ad(k)X = X}.
Let a
X
be the intersection of all maximal abelian subspaces a of p with X ∈a.Wesay
that X is regular if a
X
is a maximal abelian subspace of p, or equivalently, if there

Basic Material 419
exists a unique maximal abelian subspace of p containing X. Otherwise, we call X
singular. The isotropy subgroup K
X
is the centralizer of a
X
in K. If, in particular, g
is a split real form of g(C) and X is regular, then K ·X = K.
In general, a real flag manifold is not a Riemannian symmetric space. Consider
the real semisimple Lie algebra g equipped with the positive definite inner product
B
θ
(X,Y )=−B(X ,
θ
Y ),where
θ
is the Cartan involution on g coming from the sym-
metric space structure of G/K.For0= X ∈ p, the endomorphism ad(X) : g → g
is selfadjoint and hence has real eigenvalues. The real flag manifold K ·X is a Rie-
mannian symmetric space if and only if the eigenvalues of ad(X) are −1, 0,+1. Note
that not every real semisimple Lie algebra g admits such an element X. A real flag
manifold that is a Riema nnian symmetric space is called a symmetric R-space. If,
in addition, g is simple, then it is called an irreducible symmetric R-spa ce. Decom-
posing g into its simple parts, one easily sees that every symmetric R-space is the
Riemannian product of irreducible symmetric R-spaces.
The classification of the symmetric R-spaces was established by Kobayashi and
Nagano [177]. It follows from their classification and a result by Takeuchi [312]
that the symmetric R-spaces consist of the Hermitian symmetric spaces of com-
pact type and their real forms. A real form M of a Hermitian symmetric space
¯
M
is a connected, complete, totally real, totally geodesic submanifold of
¯
M whose real
dimension equals the complex dimension of
¯
M. These real forms were classified by
Takeuchi [312] and independently by Leung [197].
Among the irreducible symmetric R-spaces, the Hermitian symmetric spaces are
precisely those arising from simple complex Lie g roups modulo some compact real
form. This means that an irreducible symmetric R-space is a Hermitian symm etric
space or a real form precisely if the symmetric space G/K is of type IV or III, respec-
tively. The isotropy representation of a symmetric space G/K of noncompact type is
the same as the isotropy representation of its dual simply connected compact sym-
metric space. Thus, we can also characterize the Hermitian symmetric spaces among
the irreducible symmetric R-spaces as those spaces that arise as an orbit of the adjoint
representation of a sim ply connected, compact, real Lie g roup G, or equivalently, that
is a complex flag manifold. This leads to Table A.6.
TABLE A.6: Irreducible symmetric R-spaces of Hermitian type
GK·X = Ad(G) ·X Remarks
Spin
n
SO
n
/SO
2
SO
n−2
n ≥ 5
Spin
2n
SO
2n
/U
n
n ≥ 3
SU
n
SU
n
/S(U
p
U
n−p
) n ≥ 2, 1 ≤ p ≤ [
n
2
]
Sp
n
Sp
n
/U
n
n ≥ 2
E
6
E
6
/Spin
10
U
1
E
7
E
7
/E
6
U
1
The real forms are always non-Hermitian and, among the irreducible symmetric
R-spaces, they are precisely those spaces arising from the isotropy representation o f
a symmetric space G/K of type I. We list them in Table A.7.

420 Submanifolds and Holonomy
TABLE A.7: Irreducible symmetric R-spaces of non-Hermitian type
G/KK·X Remarks
SU
n
/SO
n
G
p
(R
n
) n ≥ 3, 1 ≤ p ≤ [
n
2
]
SU
2n
/Sp
n
G
p
(H
n
) n ≥ 2 , 1 ≤ p ≤ [
n
2
]
SU
2n
/S(U
n
U
n
) U
n
n ≥ 2
SO
n
/SO
p
SO
n−p
(S
p−1
×S
n−p−1
)/Z
2
n ≥ 3 , 1 ≤ p ≤ [
n
2
]
SO
2n
/SO
n
SO
n
SO
n
n ≥ 5
SO
4n
/U
2n
U
2n
/Sp
n
n ≥ 3
Sp
n
/U
n
U
n
/SO
n
n ≥ 3
Sp
2n
/Sp
n
Sp
n
Sp
n
n ≥ 2
E
6
/Sp
4
G
2
(H
4
)/Z
2
E
6
/F
4
OP
2
E
7
/SU
8
(SU
8
/Sp
4
)/Z
2
E
7
/E
6
U
1
E
6
U
1
/F
4
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
