Irrationality (1978-79)

After my demoralizing encounter with linear algebra, I thought about switching from math to physics. Then in my sophomore year I had an inspirational teacher, Elias Stein, for complex analysis, and so I went back to majoring in math again.

At some point during that year, my brother Ian had a talk with me. It’s hazy in my memory, but I picture us driving home for Thanksgiving. He was asking me about my future plans, what was I going to major in, etc., and then started trying to persuade me to take all the pre-med courses. Not this again—everyone had always told me I should be a doctor. “You like math and science,” they’d say. “And there are so many things you can do with it—some are even mathematical, like radiology.” (“And you have such nice hands,” my mother would say.)

But Ian took a different tack. He was a sharp lawyer and a great judge of people. Plus, he truly did think he was giving me good advice. He argued that I should take biology and chemistry and organic chemistry because I might actually like them. It wouldn’t commit me to becoming a doctor. It would just be so much easier to take them now rather then jam them in later. And even if I didn’t end up going to medical school, I’d still benefit from the broad science background they’d provide.

So after a lot of soul searching, I relented and gave premed a try.

Of course this was completely irrational. I had no interest in being a doctor. I wanted to be a math professor, and always had.

All of that must have been very much on my mind when I wrote to Mr. Joffray in February of 1979. But I barely mentioned it to him. After all, he was not my confidant or coach. He was someone who enjoyed my math excursions, and I guess I thought those were the rules: I’d share math problems with him.

The letter was about the irrationality of Mathematicians care about this number because it’s fundamental to geometry. It tells you how long the diagonal of a square is compared to its side. For instance, a 1’ × 1’ square has a diagonal that’s feet long.

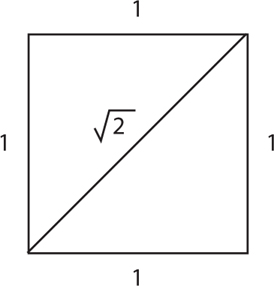
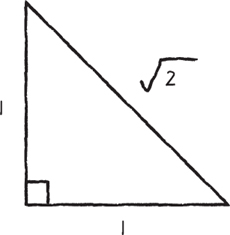
That fact comes straight from the Pythagorean theorem, which says that a right triangle with sides of length a and b has a hypotenuse of length c, where a² + b² = c². Here, we make the connection by regarding the diagonal of the square as the hypotenuse of a right triangle with sides a = 1 and b = 1. Then we get c² = 1² + 1² = 2, and hence c = is the diagonal’s length.

In ancient times, the Greeks, and probably the Babylonians and maybe the Indians and the Chinese, knew that the diagonal of a square was about 40% longer than its side, but what exactly was this basic and magical number ?

The Pythagoreans originally suspected that must be the ratio of two whole numbers, and they desperately wanted to know what those two numbers might be. This was no minor curiosity to them; it was part of an all-encompassing religion and research program founded on the mystical idea that “all is number,” that the laws of the universe could be expressed in mathematics, and more specifically, in terms of small whole numbers. Pythagoras himself had made the discovery that musical harmony was based on numbers: when he plucked two lyre strings, both strung at the same tension but one twice as long as the other, the longer string sounded a note exactly one octave lower than the shorter string. In fact, any string ratio involving small numbers, such as 2:3 or 4:3 or 5:2, produced beautiful harmony.

With this in mind, it was natural to expect that must also be the ratio of some nice whole numbers. It’s almost , but not exactly, because 5² + 5² = 25 + 25 = 50, whereas 7² = 49. Close, but not quite. Maybe two bigger numbers would work?

That’s the question. Can we find two whole numbers, m and n, such that = m / n, or equivalently, n² + n² = m²? The shocking answer is no. The square root of 2 is irrational, meaning it can’t be written as the ratio of two whole numbers. The philosophical implications were profound and disconcerting. If whole numbers were inadequate to characterize something as simple as a square’s diagonal, what hope was there for the rest of Pythagorean philosophy?

The legend goes that when one of Pythagoras’s disciples discovered the irrationality of , the cult members were so enraged that they took him out to sea and hurled him overboard.

There’s a standard proof that is irrational. You’ve probably heard people describe certain pieces of mathematics as elegant. Well, this proof is, in my opinion, not elegant, whereas the unorthodox one in the letter to Mr. Joffray is. See if you agree.

The usual proof goes like this. Suppose = m / n, where m and n are whole numbers with no common divisors. In other words, before doing anything else, we divide out any factors common to m and n so that the fraction is in “lowest terms.” We do that for cleanliness. It ensures that m and n will be as small as possible, and it avoids the confusion that could ensue if we allowed a number to be represented by several different fractions, such as 1/2 = 2/4 = 3/6. By requiring lowest terms, we make sure that fractions are represented in a unique way.

Next we’ll derive a contradiction, which will imply that it must be impossible to write = m = n for any m and n.

Okay, here goes. If

then

So now we know m must be even, which means we can write it as 2 times something, say m = 2 p, where p is a whole number.

Here comes the contradiction. Since m = 2p and m² = 2n² (from the reasoning above), we see that (2p)² = 2n², which implies 4p² = 2n². Cancel a factor of 2 to get 2p² = n². And there’s the rub. Because 2p² = n², we see that n² is also 2 times something, which means n² is even and hence n is even.

Thus, we’ve concluded that both m and n are even. That contradicts our earlier requirement that m and n have no common divisors (we’ve just shown they’re both even and hence both divisible by 2). This implies that our original assumption was wrong, and hence must, in fact, be irrational.

The logic of this proof is airtight, but there’s something annoying about it. Aside from its meandering character, the argument is unthematic. It makes the irrationality of seem like a fact about number theory, not geometry. What happened to all the shapes we started with—the squares, diagonals, and triangles?

In contrast, the proof in my letter to Mr. Joffray is purely geometric. It was shown to me by one of my teachers at Princeton, Benedict Gross.

It’s time for our annual math problem! I hope this note finds you and your family well and happy. Everything’s fine from this end—my direction is now away from teaching and toward medicine, and the pre-med courses are stimulating and competitive. But I still love mathematics best (I’m majoring in it) and couldn’t resist showing you this sly proof of an elementary fact in geometry: the irrationality of

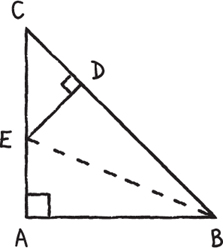
Suppose = m / n, where m and n are integers. Think of n in this way: it is the number of times we repetitively add some unit length until we achieve the length of a side.

Maybe I’m being wordy: the sides are n times the unit length, and the hypotenuse is m times, OK? Now make the following construction: mark off a length DB equal to the length of AB. Now drop the perpendicular DE (to AC) and draw in the line EB.

Claim: ΔABE ΔDBE. This follows because the triangles share , they’re both right triangles, and by construction.

Hence by corresponding parts; then ΔCDE is soon to be an isosceles right triangle—it has an angle ECD = 45^º and is a right triangle by construction. Thus , as shown by the tick marks.

So far, nothing.

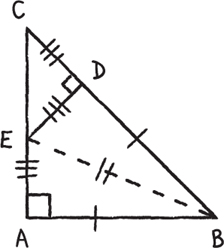
Now for the proof (I’m hoping you haven’t seen this before!).

We assumed that the lengths of and could each be expressed as a multiple of some unit length, call it l. Then consider the new, smaller isosceles right triangle CDE.

Look first at . Its length = length of minus length of ; but , so length of = (length of original hypotenuse) – (length of original side), both of which were integral multiples of the unit length l. Hence their difference is also an integral multiple of l (closure of the integers!!), and therefore we now have a smaller isosceles right triangle whose side is an integral multiple of l. Wait—we must show the same fact is true of the little hypotenuse . Its length is that of - = - , both integral multiples of l. ( = original side; is shown above to be a multiple.)

So our construction yields a smaller isosceles right triangle whose sides and hypotenuse are both multiples of the unit length. (It’s clear that the scale factor for length shrinkage is > 2; i.e., 2 times length < length .)

Hence (do you see what’s coming?) we can construct a sequence of isosceles right triangles of ever-diminishing size; in fact, we can construct a triangle of very small size but whose sides and hypotenuse are still integral multiples of the unit length l (which follows from earlier arguments).

But this is crazy! If we choose a triangle with a hypotenuse of length < l, what are we to do? No integral multiple of l (other than 0) is less than l in length—and so we have a contradiction.

Thus no such l could exist, and therefore the hypotenuse and the side are incommensurable (some nice old-fashioned language there!). This proof is due to my professor in a seminar on Fermat’s last theorem (haven’t solved it yet, by the way).

I prefer the proof to the usual one because it’s more in the geometric spirit of the question. If you get the chance, tell me what you think, and also what’s new.

So long,

Steve

P.S. Exercise for the reader: Use the method of this proof to show that the Golden Mean is irrational (i.e., the sides of the Golden Rectangle are incommensurable). Au revoir!

A turning point came soon after I’d mailed this letter.

Having been convinced by my brother to switch to premed, I was now shouldering a course load consisting of abstract algebra and differential geometry, plus freshman biology, freshman chemistry, and organic chemistry, all at the same time. Three labs a week. That’s tough for anyone, especially someone so inept in real-world things. I was always the last to leave the orgo lab. The teaching assistant hated me. “What’s taking so long,” she’d ask. “It’s just like boiling water, or cooking,” she’d say. But I’d never done those things either.

Another drag was preparing for the MCAT, the entrance test required for medical school. Because I had so much to catch up on, I’d signed up for a Kaplan review course. The nearest one was in New Brunswick—an hour away by car—and it met on Sunday mornings. Not a time a college student wants to be awake, and least of all, preparing for the MCAT.

Still, I resigned myself to the pre-med conveyor belt.

When I came home for spring vacation, my mother took one look at my face and said, “There’s something wrong. Something’s really bothering you. How’s school?”

“I like it,” I said. “It’s fine, I’m learning good stuff.”

“No, you don’t look happy. What’s the matter?”

I didn’t really know. “Maybe I’m tired,” I said. “I’m working a lot.”

“No, it’s something else. What are you going to take next year? You’ll be a senior.”

Well, that was bothering me. “Being a pre-med so late, I’m going to have to take biochemistry, vertebrate physiology, and a bunch of other courses that the med schools want. Plus I have a senior thesis and two more courses in the math department. Which means that my schedule is going to be so full that I’m not going to be able to take quantum mechanics.”

“Why does that matter to you?” she asked.

“Because that’s something I’ve wanted to learn about forever!” I blurted out. “In first grade, when the teacher would march us down to the school library and make us choose a book, I’d always choose the same one: The How and Why Wonder Book of Atomic Energy. And it’s been like that ever since. Bohr and Heisenberg, Schrödinger and Einstein—those guys are my heroes. I’ve worked my whole life to get to this point, and now I’m finally ready to learn what the Heisenberg uncertainty principle really says—not just the words, but the math. But I’m never going to get the chance to do it because I can’t fit it in, and then I’ll be in medical school, cutting up cadavers, and it’ll be too late.”

She looked at me, caught my eyes.

“What if you could just say, right now, ‘I love math and physics. I want to take quantum mechanics. I’m not going to be a doctor. I’m going to do whatever it takes to become the best math professor I can be.’ ”

And I started to cry. It was as though a tremendous weight had been lifted. Then we were both laughing and crying. I never did take the MCAT, and I’ve never looked back on that decision. Some people never find their passion. But by denying mine, I found it and became sure of it.