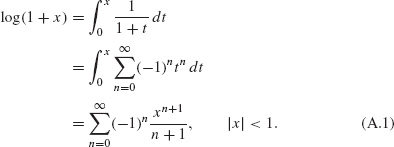Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Appendix A

Power series

We recall some results from the theory of power series which should already be known to the reader. Proofs and further results can be found in textbooks on Analysis, see e.g. [25, 26].

A.1 Basic properties

Let {a_n} be a sequence of complex numbers. The power series centred at zero with coefficients {a_n} is

i.e. the sequence of polynomials {s_n(z)}_n

Given a power series , the non-negative real number ρ defined by

where 1/0⁺ = +∞ and 1/(+∞) = 0, is called the radius of convergence of the series . In fact, one proves that the sequence {s_n(z)} is absolutely convergent if |z| < ρ and it does not converge if |z| > ρ. It can be shown that ρ > 0 if and only if the sequence {|a_n|} is not more than exponentially increasing. In this case, the sum of the series

is defined in the disc {|z| < ρ}.

Power series can be integrated and differentiated term by term. More precisely, the following holds.

Theorem A.1 Let be the sum of a power series with radius of convergence ρ. Then the series and have the same radii of convergence ρ. If ρ > 0, then A(z) is holomorphic in B(0, ρ),

and, given any piecewise C¹ curve γ : [0, 1] → B(0, ρ),

Then Corollary A.2 easily follows.

Corollary A.2 Let be the sum of a power series of radius of convergence ρ > 0. Then

Thus, if ρ > 0 the sum A(z), |z| < ρ, completely determines the sequence {a_n}. The function A(z) is called the generating function of the sequence {a_n}. In other words, {a_n} and contain the same ‘information’ (we are assuming that {a_n} grows at most exponentially or, equivalently that ρ > 0): we can say that the function A(z), |z| < ρ, is a new ‘viewpoint’ on the sequence {a_n}.

By Corollary A.2 if and B(z) = are the sums of two power series with positive radii of convergence, that coincide near zero, then a_n = b_n ∀n, both series have the same radius ρ, and A(z) = B(z) for any z such that |z| < ρ.

Example A.3 (Geometric series) The geometric series is the most classical example of power series. It generates the sequence {1, 1, 1,... }

and its sum is

Example A.4 (Exponential) Taking advantage of Taylor expansions, one can prove that

Example A.5 (Logarithm) Replacing z with −z in the equality |z| < 1, we get

Integrating along the interval [0, x] ⊂ , we get

images

A.2 Product of series

Definition A.6 The convolution product of two sequences a = {a_n} and b = {b_n} is the sequence {a ∗ b}_n defined for n = 0, 1, . . . by

In the first sum we sum over all couples (i, j) of non-negative integers such that i + j = n.

The first terms are

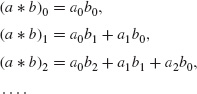
images

The convolution product is commutative, associative and bilinear. Moreover the following holds.

Theorem A.7 (Cauchy) Let a = {a_n} and b = {b_n} be two sequences and let and B(z) = be the sums of the associated power series defined for |z| < ρ_a and |z| < ρ_b, respectively. Then the power series of their convolution products converges for any z such that |z| < min(ρ_a, ρ_b) and

A.3 Banach space valued power series

Let V be a Banach space with norm || || and let {f_n} ⊂ V. Then one may consider the series, with values in V,

Let ρ ≥ 0 be defined by

As in the case of power series with complex coefficients, the power series in (A.2) absolutely converges in V for any Thus the sum of the series is a well defined function on the disc |z| < ρ of the complex plane with values in V

As for complex valued power series, one differentiates term by term Banach valued power series: the sum F(z) is a holomorphic function on the open disc |z| < ρ and

As a special case, one considers the space M_N,N () of N × N complex matrices with norm

called the maximum expansion coefficient of F. It is easy to prove that

and that M_N,N () equipped with this norm is a Banach space. Given a sequence {F_n} ⊂ M_N,N (), the associated power series

converges if |z| < ρ where

From the above, we have the following:

(i) ρ > 0 if and only if the sequence {||F_n||} grows at most exponentially fast.

(ii) If |z| < ρ, then the series (A.3) converges, both pointwise and absolutely, to a matrix F(z) ∈ M_N,N (),

i.e. we have ∀i, j ∈ {1, . . . ,N} the complex valued limits

A.3.1.1 Power expansion of the inverse of a matrix

Let P ∈ M_N,N () be a N × N square matrix with complex entries. If ||P|| |z| < 1, then Thus the series converges, both pointwisely and absolutely, to a matrix For any positive n we can write

so that

Since ||P|| |z| < 1, as n → ∞ we get

Therefore, we conclude that, if then Id − zP is invertible and

A.3.1.2 Exponential of a matrix

Let Q ∈ M_N,N (). The radius of convergence of the power series

is +∞, so that, for any z ∈ the power series converges, both absolutely and pointwisely, to a matrix denoted by e^Qz,

Proposition A.8 The following hold:

(i) e^Q0 = Id.

(ii) e^Qz and Q commute.

(iii) for any z ∈ .

(iv) e^Q(z+w) = e^Qz e^Qw for any z, w ∈ .

(v) e^Qz is invertible and its inverse is (e^Qz)⁻¹ = e^−Qz.

(vi) (e^Qz)ⁿ = e^Qnz for any z ∈ and any n ∈ .

Proof. Properties (i) and (ii) are a direct consequence of the definition of e^Qz. Property (iii) follows differentiating term by term the series . Property (iv) is a consequence of the formula for the product of power series: in fact,

images

Finally, properties (v) and (vi) are particular cases of (iv).

A.3.2 Exercises

Exercise A.9 Prove the Newton binomial theorem:

(i) directly, with an induction argument on n;

(ii) taking advantage of the Taylor expansions;

(iii) starting from the formula D((1 + z)ⁿ) = n(1 + z)ⁿ⁻¹;

(iv) starting from the identity e^t(x+y) = e^txe^ty.

Exercise A.10 Prove the following equalities:

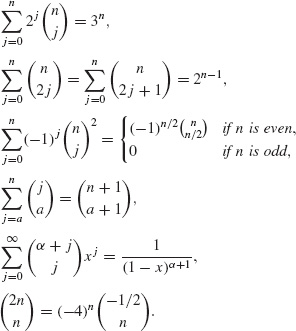
images

Exercise A.11 Show that

Exercise A.12 Let {a_n} be a complex valued sequence such that {|a_n|} grows at most exponentially fast. Let |z| < ρ be its generating function. Compute the generating function of the following sequences: