Appendix B

Measure and integration

The axiomatic approach to probability by Andrey Kolmogorov (1903–1987) makes essential use of the measure theory. In this appendix we review the aspects of the theory that are relevant to us. We do not prove everything and refer the interested reader for proofs and further study to one of the many volumes on this now classic subject, see e.g. [7, 27].

B.1   Measures

B.1.1   Basic properties

Here Ω shall denote a generic set. For a generic subset E of Ω, E^c := Ω E denotes the complement of E in Ω and (Ω) denotes the family of all subsets of Ω. A family of subsets of Ω is then a subset of (Ω), ⊂ (Ω). We say that a family ⊂ (Ω) of subsets of a set Ω is an algebra if , Ω and E ∪ F, E ∩ F and E^c whenever E, F .

Definition B.1 We say that is a σ-algebra if is an algebra and for every sequence of subsets we also have ∪_k E_k and ∩_k F_k .

In other words, if we operate on sets of a σ-algebra with differences, countable unions or intersections, we get sets of the same σ-algebra: we also say that a σ-algebra is closed with respect to differences, countable unions and intersections.

Let ⊂ (Ω) be a family of subsets of Ω. It is readily seen that the class

is again a σ-algebra, hence the smallest σ-algebra containing . We say that is the σ-algebra generated by .

Definition B.2 The smallest σ-algebra containing the open sets of is called the σ-algebra of Borel sets.

Definition B.3 A measure on Ω is a couple (, ) of a σ-algebra ⊂ (Ω) and of a map with the following properties:

(i) () = 0.

(ii) (Monotonicity) If A, B with A ⊂ B, then (A) ≤ (B).

(iii) (σ-additivity) For any disjoint sequence we have

Obviously (iii) reduces to finite additivity for pairwise disjoint subsets if is finite. When is infinite, the infinite sum on the right-hand side is understood as the sum of a series of non-negative terms. From Definition B.3 we easily get the following.

Proposition B.4 Let (, ) be a measure on Ω. We have:

(i) If A , then 0 ≤ (A).

(ii) If A, B with A ⊂ B, then (B A) + (A) = (B).

(iii) If A, B then (A ∪ B) + (A ∩ B) = (A) + (B).

(iv) If A, B then (A ∪ B) ≤ (A) + (B).

(v) (σ-subadditivity) For any sequence we have

(vi) (Disintegration formula) If is a partition of Ω, then for every A ⊂ Ω,

(vii) (Continuity)

(a) If with E_i ⊂ E_i+1 ∀i, then and

(b) Let be such that E_i ⊃ E_i+1 ∀i. Then and more-over, if (E₁) < +∞, then

Proof. (i)–(vi) follow trivially from the definition of measure. Let us prove claim (a) of (vii). Since (E_k) ≤ (∪_k E_k) for every k, the claim is trivial if for some k (E_k) = +∞. We may therefore assume (E_k) < ∞ for all k. We set E := ∪_k E_k and decompose E as

The sets E₁ and E_k E_k−1, k ≥ 1, are of course in and pairwise disjoint. Because of the σ-additivity of we then have

Claim (b) of (vii) easily follows. In fact, since (E₁) < +∞ and E_k ⊂ E₁, we have (E_k) = (E₁) − (E₁ E_k) for all k. Since is an increasing sequence of sets, we deduce from (a) that

Let (, ) be a measure on Ω. We say that N ⊂ Ω is -negligible, or simply a null set, if there exists E such that N ⊂ E and (E) = 0. Let be the collection of all the subsets of Ω of the form F = E ∪ N where E and N is -negligible. It is easy to check that is a σ-algebra which is called the -completion of . Moreover, setting (F) := (E) if F = E ∪ N , then (, ) is also a measure on Ω called the -completion of (, ). It is often customary to consider measures as -complete measures.

B.1.2   Construction of measures

B.1.2.1   Uniqueness

Let (, ) be a measure on Ω. The σ-additivity property of suggests that the values of on are in fact determined by the values of on a restricted class of subsets of .

Definition B.5 A family ⊂ (Ω) of subsets of Ω is said to be closed under finite intersections if A, B implies A ∩ B .

A set function is σ-finite if there exists a sequence such that Ω = ∪_k I_k and α(I_k) < ∞ ∀k.

We have the following coincidence criterion. A proof can be found in, e.g. [7].

Theorem B.6 (Coincidence criterion) Let and be two measures on Ω and let be a family that is closed under finite intersections. Assume that ₁ (A) = ₂(A) ∀A and that there exists a sequence such that Ω = ∪_h D_h and ₁(D_h) = ₂(D_h) < +∞ for any h. Then ₁ and ₂ coincide on the σ-algebra generated by .

Corollary B.7 (Uniqueness of extension) Let Ω be an open set, let be a family of subsets of Ω closed under finite intersections and let be σ-finite. Then α has at most one extension to the σ-algebra generated by such that (, μ) is a measure.

B.1.2.2   Carathéodory Method I

We now present the so-called Method I for constructing measures.

Let be a family of subsets of Ω containing the empty set, and let be a set function such that α() = 0. For any E ⊂ Ω set

Of course, we set μ*(E) = +∞ if no covering of E by subsets in exists. It is easy to check that μ*() = 0, that μ* is monotone increasing and that μ* is σ-subadditive, i.e.

for every denumerable family of subsets of Ω.

We now define a σ-algebra on which μ* is σ-additive. A first attempt is to choose the class of sets on which μ* is σ-additive, i.e. the class of sets E such that

μ*(B ∪ E) = μ*(E) + μ*(B)

for every subset B disjoint from E, or, equivalently such that

However, in general, this class is not a σ-algebra. Following Carathéodory, a localization of (B.6) suffices. A set E ⊂ Ω is said to be μ* -measurable if

and the class of μ* -measurable sets will be denoted by .

Theorem B.8 (Carathéodory) is a σ-algebra and μ* is σ-additive on . In other words, (, μ*) is a measure on Ω.

Without additional hypotheses both on and α, we might end up with not included in or with a μ* that is not an extension of α.

Definition B.9 A family ⊂ (Ω) of subsets of Ω is a semiring if:

(i) .

(ii) For any E, F we have E ∩ F .

(iii) If E, F , then where the I_j’s are pairwise disjoint elements in .

Notice that, if E, F , then E ∪ F decomposes as where I₁, . . ., I_n belong to and are pairwise disjoint.

Theorem B.10 (Carathéodory) Let ⊂ (Ω) be a semiring of subsets of Ω, let be a σ-additive set function such that α() = 0 and let (, μ*) be the measure constructed by the above starting from and α. Then:

(i) ⊂ .

(ii) μ* extends α to .

(iii) Let E ⊂ Ω with μ*(E) < ∞. Then E if and only if E = ∩_k F_k N where μ*(N) = 0, is a decreasing sequence of sets F_k and, for k ≥ 1, F_k is a disjoint union F_k = ∪_j I_k,j of sets I_k,j .

Assume be such that is a semiring, α is σ-additive and σ-finite and let be the σ-algebra generated by . From Theorems B.6 and B.10 the following easily follows:

• (iii) of Theorem B.10 implies that is the μ* -completion of : every set A has the form A = E ∪ N where E and μ* (N) = 0.
• Corollary B.7 imples that (, μ*) is the unique measure that extends α to .

B.1.2.3   Lebesgue measure in

A right-closed interval I of , n ≥ 1, is the product of n intervals closed to the right and open to the left, . The elementary volume of this interval is .

An induction argument on the dimension n shows that is a semiring. For instance, let n = 2 and let A, B, C, D be right-closed intervals on . Then

The family of right-closed intervals of will be denoted by . We know that is the σ-algebra generated by , see Exercise B.16. Since is trivially closed under finite intersections, we infer from Theorem B.6 that two measures that coincide on and that are finite on bounded open sets coincide on every Borel set .

Proposition B.11 The volume map is a σ-additive set function.

Proof. It is easily seen that the elementary measure | | is finitely additive on intervals. Let us prove that it is σ-subadditive. For that, let I, I_k be intervals with I = ∪_k I_k and, for > 0 and any k denote by J_k an interval centred as I_k that contains strictly I_k with |J_k| ≤ |I_k| + 2^−k. The family of open sets covers the compact set , hence we can select k₁, k₂, . . . k_N such that concluding

i.e. that || is σ-subadditive on .

Suppose now that I = ∪_k I_k where the ’s are pairwise disjoint. Of course, by the σ-subadditivity property of ||, . On the other hand, for any integer N. Finite additivity then yields

and, as N → ∞, also the opposite inequality .

Taking advantage of Proposition B.11, Theorem B.10 applies. We get the existence of a unique measure that is finite on bounded open sets, called the Lebesgue measure on , that extends to Borel sets the elementary measure of intervals. From (B.5) we also get a formula for the measure of a Borel set ,

B.1.2.4   Stieltjes–Lebesgue measure

Proposition B.12 Let F : → be a right-continuous and monotone nondecreasing function. Then the set function ζ : → defined by ζ(]a, b]) := F (b) − F (a) on the class of right-closed intervals is σ-additive.

Proof. Obviously, ζ is additive and monotone increasing, hence finitely sub-additive, on . We now prove that ζ is σ-additive. Let , I_i :=]x_i, y_i], be a disjoint partition of I :=]a, b]. Since ζ is additive, we get

Let us prove the opposite inequality. For > 0, let be such that F (y_i + δ_i) ≤ F(y_i) + 2^–i. The open intervals ]x_i, y_i + δ_i[ form an open covering of [a + , b], hence finitely many among them cover again [a + , b]. Therefore, by the finite subadditivity of ζ,

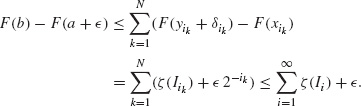
Letting go to zero, we conclude

Example B.13 If F is not right-continuous, the set function ζ : → , ζ(]a, b]) := F(b) − F (a) is not in general subadditive. For instance, for 0 ≤ a ≤ 1, set

Let , clearly , but

as soon as a < 1.

Theorem B.14 (Lebesgue) The following hold:

(i) Let ((), ) be a finite measure on . Then the law F (t) := (] − ∞, t]), t , is real valued, monotone nondecreasing and right-continuous.

(ii) Let F : → be a real valued, monotone nonderecreasing and right-continuous function. Then there exists a unique measure ((), ) finite on bounded sets of such that

Proof. (i) F is real valued since ((), ) is finite on bounded Borel sets. Moreover, monotonicity property of measures implies that F is monotone nondecreasing. Let us prove that F is right-continuous. Let t and let be a monotone decreasing sequence such that t_n ↓ t. Since ] − ∞, t] = and is finite, one gets F(t_n) = (] − ∞, t_n]) → (] − ∞, t]) = F(t) by the continuity property of measures.

(ii) Assume F (t) is right-continuous and monotone nondecreasing. Let be the semiring of right-closed intervals. The set function , ζ([a, b]) := F (b) − F (a) is σ-additive, see Proposition B.12. Therefore Theorem B.6 and B.10 apply and ζ extends in a unique way to a measure on the σ-algebra generated by , i.e. on (), that is finite on bounded open sets.

The measure ((),) in Theorem B.14 is called the Stieltjes–Lebesgue measure associated with the right-continuous monotone nondecreasing function F.

B.1.2.5   Approximation of Borel sets

Borel sets are quite complicated if compared with open sets that are simply denumerable unions of closed cubes with disjoint interiors. However, the following holds.

Theorem B.15 Let be a measure on that is finite on bounded open sets. Then for any

In particular, if has finite measure, (E) < +∞, then for every > 0 there exists an open set Ω and a compact set K such that K ⊂ E ⊂ Ω and (Ω K) < .

Although the result can be derived from (iii) of Theorem B.10, it is actually independent of it. We give here a proof that does not use Theorem B.10.

Proof. Step 1. Let us prove the claim assuming is finite. Consider the family

Of course, contains the family of open sets. We prove that is closed under denumerable unions and intersections. Let and, for > 0 and j = 1, 2, . . ., let A_j be open sets with A_j ⊃ E_j and (A_j) ≤ (E_j) + 2^–j, that we rewrite as (A_j E_j) < 2^–j since E_j and A_j are measurable with finite measure. Since

we infer

where A := ∪_j A_j and B := ∩_j A_j. Since A is open and A ⊃ ∪_j E_j, the first inequality of (B.10) yields ∪_j E_j . On the other hand, is open, contains ∩_j E_j and, by the second inequality of (B.10), for sufficiently large N. Therefore ∩_j E_j .

Moreover, since every closed set is the intersection of a denumerable family of open sets, also contains all closed sets. In particular, the family

is a σ-algebra that contains the family of open sets. Consequently, and (B.8) holds for all Borel sets of Ω.

Since (B.9) for E is (B.8) for E^c, we have also proved (B.9).

Step 2. Let us prove (B.8) and (B.9) for measures that are finite on bounded open sets. Let us introduce the following notation: given a Borel set , define the restriction of to A as the set function

It is easily seen that is a measure on that is finite if (A) < ∞.

Let us prove (B.8). We may assume (E) < +∞ since otherwise (B.8) is trivial. Let V_j := B(0, j) be the open ball centred at 0 or radius j. The measures are Borel and . Step 1 then yields that for any > 0 there are open sets A_j with A_j ⊃ E and . The set A := ∪_j(A_j ∩ V_j) is open, A ⊃ E and, by the subadditivity of

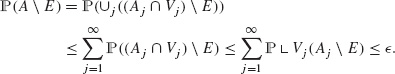
Let us prove (B.9). The claim easily follows applying Step 1 to the measure If (E) < +∞. IF (E) = +∞, then E = ∪_j E_j with E_j measurable (E_j) < +∞, then for every > 0 and every j there exists a closed set F_j with F_j ⊂ E_j and . The set F := ∪_j F_j is contained in E and

hence, for sufficiently large N, is closed and .

Step 3. By assumption, and (E) < + ∞. By Step 2 for each > 0 there exists an open set Ω and a closed set F such that F ⊂ E ⊂ Ω and

, so that . Setting K := with large enough n, we still get

thus concluding that A ⊃ E ⊃ K and (A K) < 3 .

B.1.3   Exercises

Exercise B.16 Show that () is the smallest σ-algebra generated by one of the following families of sets:

• the closed sets;
• the open intervals;
• the closed intervals;
• the intervals ]a, b], a, b , a < b;
• the intervals [a, b[, a, b , a < b;
• the closed half-lines ] − ∞, t], t .

Solution. [Hint. Show that any open set can be written as the union of an at most denumerable family of intervals.]

Exercise B.17 The law of a finite measure on is defined by

Show that two finite measures and on coincide if and only if the corresponding laws agree.

B.2   Measurable functions and integration

Characterizing the class of Riemann integrable functions and understanding the range of applicability of the fundamental theorem of calculus were the problems that led to measures and to a more general notion of integral due to Henri Lebesgue (1875–1941). The approach we follow here, which is very well adapted to calculus of probability, is to start with a measure and define the associated notion of integral.

The basic idea is the following. Suppose one wants to compute the area of the subgraph of a non-negative function f : → . One can do it by approximating the subgraph in two different ways, see Figure B.1. One can take partitions of the x axis, and approximate the integral by the area of a piecewise constant function as we do when defining the Riemann integral, or one can take a partition of the y axis, and approximate the area of the subgraph by the areas of the strips. The latter defines the area of the subgraph as

Figure B.1 The computation of an integral according to (a) Riemann and (b) Lebesgue.

where

is the t upper level of f and |E_f,t| denotes its ‘measure’. Since t → |E_f,t| is monotone nonincreasing, hence Riemann integrable, (B.12) suggests defining the integral by means of the Cavalieri formula

From this point of view, it is clear that the notion of integral makes essential use of a measure on the domain, that must be able to measure even irregular sets, since the upper levels can be very irregular, for instance if the function is oscillating.

In the following, instead of defining the integral by means of (B.13), we adopt a slightly more direct approach to the integral and then prove (B.13).

B.2.1   Measurable functions

Definition B.18 Let be a σ-algebra of subsets of a set Ω. We say that is -measurable if for any t we have

There are several equivalent ways to say that a function is -measurable. Taking advantage of the fact that is a σ-algebra, one proves that the following are equivalent:

(i) {x Ω | f (x) > t} for any t.

(ii) {x Ω | f (x) ≥ t} for any t.

(iii) {x Ω | f (x) ≤ t} for any t.

(iv) {x Ω | f (x) < t} for any t.

Moreover, in the previous statements one can substitute ‘for any t’ with ‘for any t in a dense subset of ’, in particular, with ‘for any t ’.

Since any open set of is an at most denumerable union of intervals, the following are also equivalent:

(i) {x Ω | f (x) > t} for any t.

(ii) For any open set A ⊂ we have f⁻¹ (A) .

(iii) For any closed F ⊂ we have f⁻¹ (F) .

(iv) For any Borel set B ⊂ we have f⁻¹(B) .

The three last statements are independent of the ordering relation of . They suggest the following extension.

Definition B.19 Let be a σ-algebra of subsets of a set Ω. A vector valued function , N ≥ 1, is -measurable if one of the following holds:

(i) For any open set A ⊂ we have f⁻¹(A) .

(ii) For any closed set F ⊂ we have f⁻¹(F) .

(iii) For any Borel set B ⊂ we have f⁻¹(B) .

In general, not every function is -measurable. However, since is a σ-algebra, one can prove that the algebraic manipulations as well as the pointwise limits of -measurable functions always result in -measurable functions. For instance, if f and g are -measurable and α , then the functions

are -measurable. Moreover, let be a sequence of -measurable functions. Then:

• The functions

  

  are 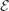-measurable.

• Let 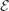⊂ Ω be the set

  

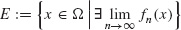
  and let f (x) := lim_n→∞ f_n(x), x E. Then E and for any t we have {x E | f (x) > t} .

Recalling that a function : X → Y between metric spaces is continuous if and only if for any open set A ⊂ Y the set ⁻¹ (A) ⊂ X is open, we get immediately the following:

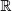• Continuous functions g : ^N → ^m are 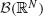-measurable,
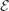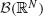• Let be -measurable and let be - measurable, then ○ f is 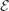-measurable.

In particular, (ii) implies that |f|^p, log |f |, . . . are -measurable functions if f is -measurable and that , f = (f¹, . . ., f^N) is -measurable if and only if its components f¹, . . ., f^N are -measurable.

Let (, ) be a measure on Ω. A simple function φ : Ω → is a function with a finite range and -measurable level sets, that is,

The class of simple functions will be denoted by . Simple functions being linear combinations of -measurable functions are -measurable.

Proposition B.20 (Sampling) Let be a σ-algebra of subsets of a set Ω. A non-negative function is -measurable if and only if there exists a nondecreasing sequence of non-negative simple functions such that φ_k(x) ↑ f(x) ∀x Ω.

Proof. Let f be the pointwise limit of a sequence of simple functions. Since every φ_k is -measurable, then f is -measurable.

Conversely, let f : Ω → be a function. By sampling f, we then construct a sequence of functions with finite range approaching f, see Figure B.1. More precisely, let and for h = 0, 1,, . . . 4^k − 1, let

Define φ_k: Ω → as

By definition, , moreover, , since passing from k to k + 1 we half the sampling intervals. Let us prove that . If f (x) = +∞, then φ_k(x) = 2^k ∀k, hence φ_k(x) → +∞ = f(x). If f(x) < +∞, then for sufficiently large k, f(x) ≤ 2^k, hence there exists such that x E_k,h. Therefore,

Passing to the limit as k → ∞ we get again φ_k(x) → f(x).

The previous construction applies to any non-negative function . To conclude, notice that if f is -measurable, then the sets E_k and E_k,h are -measurable for every k, h. Since

φ_k is a simple function.

B.2.2   The integral

Let (, ) be a measure on Ω. For any simple function φ : Ω → , one defines the integral of φ with respect to the measure (, ) as

as intuition suggests. Since a priori (φ = a_j) may be infinite, we adopt the convention that a_j(φ = a_j) := 0 if a_j = 0. Notice that the integral may be infinite.

We then define the integral of a non-negative -measurable function with respect to (, ) as

For a generic -measurable function , decompose f as f(x) = f₊(x) − f₋(x) where

f₊(x) := max(f (x), 0),         f₋(x) := max(−f(x), 0),

and define

provided that at least one of the integrals on the right-hand side of (B.17) is finite. In this case one says that f is integrable with respect to (, ). If both the integrals on the right-hand side of (B.17) are finite, then one says that f is summable. Notice that for functions that do not change sign, integrability is equivalent to measurability.

Since |f(x)| = f₊(x) + f₋(x) and f₊(x), f₋(x) ≤ |f(x)|, it is easy to check that if f is -measurable then so is |f|, and f is summable if and only if f is -measurable and . Moreover,

The class of summable functions will be denoted by or simply by when the measure is understood.

When , one refers to the integral with respect to the Lebesgue measure in (B.17) as the Lebesgue integral.

Finally, let f : Ω → be a function and let E . One says that f is measurable on E, integrable on E, and summable on E if f(x)χ_E(x) is -measurable, integrable, and summable, respectively. If f is integrable on E, one sets

In particular,

B.2.3   Properties of the integral

From the definition of integral with respect to the measure (, ) and taking also advantage of the σ-additivity of the measure one gets the following.

Theorem B.21 Let (, ) be a measure on Ω.

(i) For any c and f integrable on E, we have .

(ii) (Monotonicity) Let f, g be two integrable functions such that f(x) ≤ g(x) ∀ x Ω. Then

(iii) (Continuity, the Beppo Levi theorem) Let be a nondecreasing sequence of non-negative -measurable functions and let f(x) := lim_k→∞ f_k(x) be the pointwise limit of the f_k’s. Then f is integrable and

(iv) (Linearity) is a vector space and the integral is a linear operator on it: for f, and α, β we have

A few comments on the Beppo Levi theorem are appropriate. Notice that the measurability assumption is on the sequence . The measurability of the limit f is for free, thanks to the fact that is a σ-algebra. Moreover, the integrals in (B.19) may be infinite, and the equality is in both directions: we can compute one side of the equality in (B.19) and conclude that the other side has the same value. The Beppo Levi theorem is of course strictly related to the continuity property of measures, and at the end, to the σ-additivity of measures.

Proof of theorem B.21. (i) and (ii) are trivial.

(iii) Let us prove the Beppo Levi theorem. Since f is the pointwise limit of -measurable functions, f is -measurable. Moreover, since f_k(x) ≤ f(x) for any x Ω and every k, from (i) we infer . We now prove the opposite inequality

Assume without loss of generality that α < +∞. Let be a simple function, , such that ≤ f and let β be a real number, 0 < β < 1. For k = 1, 2, ... set

is a nondecreasing sequence of measurable sets such that ∪_k A_k = Ω. Hence, from (B.15) and the continuity property of measures

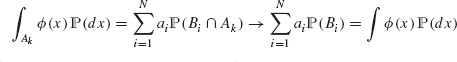
as k → ∞. On the other hand, for any k we have

Therefore, passing to the limit first as k → ∞ in (B.20) and then letting β → 1⁻ we get

Since the previous inequality holds for any simple function below f, the definition of integral yields , as required.

(iv) We have already proved the linearity of the integral on the class of simple functions, see Proposition 2.28. To prove (iv), it suffices to approximate f and g by simple functions, see Proposition B.20, and then pass to the limit using (iii).

We conclude with a few simple consequences.

Proposition B.22 Let (, ) be a measure on Ω.

(i) Let E have finite measure and let f : → be an integrable function on E such that |f(x)| ≤ M for any x E. Then f is summable on E and .

(ii) Let E, F and let f : E ∪ F → be an integrable function on E ∪ F. Then f is integrable both on E and F and

B.2.4   Cavalieri formula

Theorem B.23 (Cavalieri formula) Let (, ) be a measure on Ω. For any non-negative -measurable function we have

As usual, we shorten the notation ({x Ω | f(x) > t}) to (f > t).

Proof. Let us prove the claim for non-negative simple functions. Assume , where the sets are measurable and pairwise disjoint. For i = 1, . . ., N let . For the piecewise (hence simple) function we have

hence, integrating with respect to t

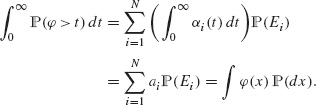
Assume now f : Ω → is non-negative and -measurable. Proposition B.20 yields a nondecreasing sequence of non-negative simple functions such that φ_k(x) ↑ f(x) pointwisely. As shown before, for each k = 1, 2, . . .

Since φ_k ↑ f(x) and (φ_k > t) ↑ (f > t) as k goes to ∞, we can pass to the limit in the previous equality using the Beppo Levi theorem to get

The claim then follows, t → (f > t), being nondecreasing, is Riemann integrable and Riemann and Lebesgue integrals of Riemann integrable functions coincide.

Corollary B.24 Let f : Ω → be integrable and for any t , let F (t) := (f ≤ t). Then

Proof. Apply (B.22) to the positive and negative parts of f and sum the resulting equalities.

B.2.5   Markov inequality

Let (, ) be a measure on Ω. From the monotonicity of the integral one deduces that for any non-negative measurable function f : Ω → we have the inequality

i.e.

This last inequality has different names: Markov inequality, weak estimate or Chebyshev inequality.

B.2.6   Null sets and the integral

Let (, ) be a measure on Ω.

Definition B.25 We say that a set N ⊂ Ω is a null set if there exists F such that N ⊂ F and (F) = 0. We say that a predicate p(x), x Ω, is true for -almost every x or -a.e., and we write ‘p(x) is true a.e.’ if the set

is a null set.

In particular, given an -measurable function f : Ω → , we say that ‘f = 0 -a.e.’ or that ‘f(x) = 0 for -almost every x Ω’ if the set {x Ω | f(x) ≠ 0} has zero measure,

Similarly, one says that ‘|f| ≤ M -a.e.’ or that ‘|f(x)| ≤ M for -almost every x’, if ({x Ω || f(x)| > M}) = 0. From the σ-additivity of the measure, we immediately get the following.

Proposition B.26 Let (, ) be a measure on Ω and let f : Ω → be a -measurable function.

(i) If , then |f(x)| < +∞ -a.e.

(ii) if and only if f(x) = 0 for -almost every x Ω.

Proof. (i) Let . Markov inequality yields for any positive integer k

Hence, passing to the limit as k → ∞ we infer that ({x Ω | f(x) = +∞}) = 0.

(ii) If f(x) = 0 for almost every x Ω, then every simple function φ such that φ ≤ |f|, is nonzero on at most a null set. Thus and, by the definition of the integral of |f|, .

Conversely, from the Markov inequality we get for any positive integer k

so that ({x Ω ||f(x)| > 1/k}) = 0. Since

passing to the limit as k → ∞ thanks to the continuity property of the measure, we conclude that ({x Ω ||f(x)| > 0}) = 0, i.e. |f(x)| = 0 -a.e.

B.2.7   Push forward of a measure

Let (, ) be a measure on Ω and let be an -measurable function. Since inverse images of Borel sets are -measurable, we define a set function on , also denoted by f_#, by

called the pushforward or image of the measure . It is easy to check the following.

Proposition B.27 is a measure on and for every non-negative Borel function φ on we have

Proof. We essentially repeat the proof of Theorem 3.9. For the reader’s convenience, we outline it again.

The σ-additivity of f_# follows from the σ-additivity of using the De Morgan formulas and the relations

which are true for any family of subsets of .

In order to prove (B.25), we first consider the case in which φ is a simple function, where c₁, ..., c_n are distinct constants and the level sets , i = 1, ..., n, are measurable. then

so that

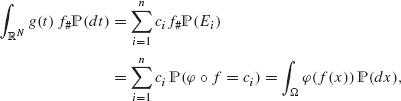
i.e. (B.25) holds when φ is simple.

Let now φ be a non-negative measurable function. Proposition B.20 yields an increasing sequence of simple functions pointwisely converging to φ. Since for every k we have already proved that

we can pass to the limit as k → ∞ and take advantage of the Beppo Levi theorem to get (B.25).

Pushforward of measures can be composed. Let (, ) be a measure on Ω, let be -measurable and let be (^N)-measurable. Then from (B.24) we infer

From (B.25) we infer the following relations for the associated integrals

for every non-negative, -measurable function , see Theorem 4.6.

B.2.8   Exercises

Exercise B.28 Let be a σ-algebra of subsets of a set Ω and let f, g : Ω → be -measurable. Then {x ∈ Ω | f (x) > g(x)} .

Solution. For any rational number r , the set A_r := {x Ω | f (x) > r, g(x) < r} belongs to . Moreover,

Thus {x | f (x) > g(x)} is a denumerable union of sets in .

Exercise B.29 Let be a σ-algebra of subsets of a set Ω, let E and let f, g : Ω → be two -measurable functions. Then the function

is -measurable.

Exercise B.30 Let be a σ-algebra of subsets of a set Ω, let f : Ω → be -measurable and let E be such that (E) < ∞. Then for at most a denumerable set of t’s.

Exercise B.31 Show that if φ is a simple function, then .

Exercise B.32 (Discrete value functions) Let (, ) be a measure on a set Ω. Let X : Ω → be an -measurable non-negative function with discrete values, i.e. X(Ω) is a countable set . Give an explicit formula for .

Solution. Let . Then

Given x, the series has only one addendum since only one set E_j contains x.

If X has a finite range, then X is a simple function so that by definition

If X(Ω) is denumerable, then for any non-negative integer k we have

Since X is non-negative, we can apply the Beppo Levi theorem and, as k → ∞, we get

Formula (B.29) can also be written as

since (X = t) = 0 if .

Exercise B.33 Let (, ) be a measure on a set Ω and let X : Ω → be an -measurable non-negative function with discrete values and such that +∞ X(Ω). Give an explicit formula for .

Solution. Let ∪ {+∞} be the range of X. For k ≥ 1, let E_k := {x | X(x) = a_k}, so that

and . From Exercise B.32,

Moreover,

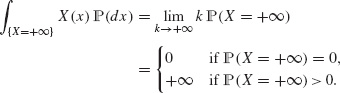
Thus

Exercise B.34 (Integral on countable sets) Let (, ) be a measure on a finite or denumerable set Ω. Denote by p : Ω → , p(x) := ({x}), its mass density. Let X : Ω → be a non-negative function. Give an explicit formula for .

Solution. Let be the range of X. By (B.29)

Exercise B.35 (Dirac delta) Let Ω be a set and let x₀ Ω. The set function such that

is called the Dirac delta [named after Paul Dirac (1902–1984)] at x₀, and is a probability measure on Ω. Prove that for any X : Ω → ,

Exercise B.36 (Sum of measures) Let (, α) and (, β) be two measures on Ω and let λ, .

(i) Show that λα + μβ : → defined by (λα + μβ)(E) := λα(E) + μβ(E) ∀E is such that (, λα + μβ) is a measure on Ω.

(ii) Show that for amy -measurable non-negative function

Solution. We first consider the case when f is a non-negative simple function: where , c_i ≥ 0. Thus

When f is an -measurable non-negative function, we approximate it from below with an increasing sequence of simple functions that pointwise converges to f(x). Since any φ_k is simple, we have

Letting k → +∞ and taking advantage of the Beppo Levi theorem we get (B.32).

Example B.37 (Counting measure) Let Ω be a set. Given a subset A ⊂ Ω let ⁰(A) := |A| be the cardinality of A. It is easy to see that ((Ω), ⁰) is a measure on Ω, called counting measure. Clearly,

where the sum on the right-hand side is +∞ if A has infinite many points. The corresponding integral is

The formula above is obvious if f is nonzero on a finite set only and can be proven by passing to the limit and taking advantage of the Beppo Levi theorem in the general case.

Exercise B.38 (Absolutely continuous measures) Let (, ) be an absolutely continuous measure with respect to the Lebesgue measure, i.e. assume there exists a summable function such that

Show that, for any non-negative ()-measurable function f,

Solution. Assume f is simple, i.e. . Then

The general case can be proven by an approximation argument, using Proposition B.20 and the Beppo Levi theorem.

B.3   Product measures and iterated integrals

B.3.1   Product measures

Let (, ) and (, ) be measures on two sets X and Y, respectively. Denote by the family of all ‘rectangles’ in the Cartesian product X × Y

and let be the set function that maps any rectangle A × B into ζ(A × B) := (A)(B). The following can be easily shown.

Proposition B.39 is a semiring and ζ : → is a σ-additive set function.

Proof. It is quite trivial to show that is a semiring. In fact, if E := A × B and F := C × D , then E ∩ F = (A ∩ C) × (B ∩ D) and

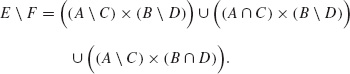
Let us prove that ζ is σ-additive. Let × F = ∪_k(E_k × F_k), E, E_k , F, F_k be such that the sets are pairwise disjoint so that

Integrating with respect to on Y and applying the Beppo Levi theorem, we obtain

Moreover, integrating with respect to on X and again by the Beppo Levi theorem we get

Thus, see Theorem B.10, ζ extends to a measure denoted (, × ) on the smallest σ-algebra containing . This measure is called the product measure of (, ) and (, ). Moreover, such an extension is unique, provided ζ : → ₊ is σ-finite, see Theorem B.6. This happens in particular, if both (, ) and (, ) are σ-finite.

Of course one can consider the product of finitely many measures. Taking for instance the product of n Bernoulli trials, one obtains the Bernoulli distribution on {0, 1}ⁿ

B.3.1.1   Infinite Bernoulli process

Let (Ω, , ) be a probability measure on Ω. Consider the set of Ω-valued sequences, and consider the family ⊂ (Ω^∞) of sets E ⊂ Ω^∞ of the form

where E_i ∀i and E_i = Ω except for a finite number of indexes, i.e. the family of ‘cylinders’ with the terminology of Section 2.2.7. Define also α : → [0, 1] by setting for ,

Notice that the product is actually a finite product, since (E_i) = 1 except for a finite number of indexes.

The following theorem holds. The interested reader may find a proof in, e.g. [7].

Theorem B.40 (Kolmogorov) is a semiring and α is σ-additive on .

Therefore, Theorem B.6 and B.10 apply so that there exists a unique probability measure (, ^∞) on Ω^∞ that extends α to the σ-algebra generated by .

The existence and uniqueness of the Bernoulli distribution of parameter p introduced in Section 2.2.7 is a particular case of the previous statement. One obtains it by choosing the Bernoulli trial distribution B(1, p) on {0, 1} as starting probability space (Ω, , ).

B.3.2   Reduction formulas

Let A ⊂ X × Y. For any point x A let A_x be the subset of Y defined as

A_x is called the section of A at x.

Theorem B.41 (Fubini) Let X, Y be two sets and let (, × ) be the product measure on X × Y of the two σ-finite measures (, ) and (, ) on X and Y, respectively. Then, for any A the following hold:

(i) A_x -a.e. x X.

(ii) x (A_x) is an -measurable function.

(iii) .

Changing the roles of the two variables, one also has:

(iv) A_y -a.e. y Y.

(v) y (A_y) is an -measurable function.

(vi) .

From the Fubini theorem, Theorem B.41, one obtains the following reduction formulas.

Theorem B.42 (Fubini–Tonelli) Let (, ) and (, ) be two σ-finite measures on the sets X and Y, respectively, and let (, × ) be the product measure on X × Y. Let f : X × Y → be -measurable and non-negative (respectively, × summable). Then the following hold:

(i) y f (x, y) is -measurable (respectively, -summable) -a.e. x X.

(ii) is -measurable (respectively, -summable).

(iii) We have

Of course, the two variables can be interchanged, so under the same assumption of Theorem B.42 we also have:

(i) x f(x, y) is -measurable (respectively, -summable) -a.e. y Y.

(ii) is -measurable (respectively, -summable).

(iii) We have

Proof. The proof is done in three steps.

(i) If f is the characteristic function of a × measurable set, then we apply the Fubini theorem, Theorem B.41. Because of additivity, the result still holds true for any -measurable simple function f.

(ii) If f is non-negative, then f can be approximated from below by an increasing sequence of simple functions. Applying the Beppo Levi theorem and the continuity of measures, the result holds true for f.

(iii) If f is × summable, then one applies the result of Step (ii) to the positive and negative parts f₊ and f₋ of f.

Notice that the finiteness assumption on the two measures (, ) and (, ) in Theorems B.41 and B.42 cannot be dropped as the following example shows.

Example B.43 Let X = Y = , , and let be the measure that counts the points: (A) = |A|. Let S := {(x, x) | x [0, 1]} and let f(x, y) = χ_S(x, y) be its characteristic function. S is closed, hence S belongs to the smallest σ-algebra generated by ‘intervals’, i.e. (²). Clearly ( × )(S) = ∞, but

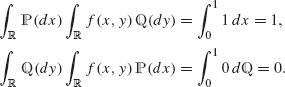
B.3.3   Exercises

Exercise B.44 Show that on the Borel sets of .

Exercise B.45 Let (, ) be a measure on Ω and let be a -measurable function. Show that the subgraph of f

is × -measurable and

[Hint. Prove the claim for simple functions and use an approximation argument for the general case.]

B.4   Convergence theorems

B.4.1   Almost everywhere convergence

Definition B.46 Let (, ) be a measure on Ω and let and X be -measurable functions.

(i) We say that converges in measure to X, if for any δ > 0

(ii) We say that converges to X almost everywhere, and we write X_n → X -a.e., if the measure of the set

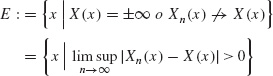
is null, (E) = 0.

The difference between the above defined convergences becomes clear if one first considers the following sets, which can be constructed starting from a given sequence of sets ; namely, the sets

In the following proposition we collect the elementary properties of such sets.

Proposition B.47 We have the following:

(i) x lim inf_n A_n if and only if there exists such that x A_n ∀n ≥ .

(ii) x lim sup_n A_n if and only if there exists infinite values of n such that x A_n.

(iii) x (Ωlim sup_n A_n)^c if and only if is finite.

(iv) .

(v) Let be a σ-algebra of subsets of Ω. If ⊂ , then both lim inf_n A_n and lim sup_n A_n are -measurable. Moreover,

Proof. (i) and (ii) agree with the definitions of lim inf_n A_n and lim sup_n A_n, respectively. (iii) is a rewrite of (ii) and (iv) is a consequence of De Moivre formulas. To prove (v) it suffices to observe that the -measurability of lim inf_n A_n and lim sup_n A_n comes from the properties of σ-algebras and that the inequality in (v) is a consequence of the continuity of measures.

Let (, ) be a measure on Ω and let and X be -measurable functions. Given any δ ≥ 0, define

Since x E_δ if and only if there exists a sequence such that |X_kn(x) − X(x)| > δ, then

Proposition B.48 Let (, ) be a measure on Ω and let and X be -measurable functions. With the notation above, converges to X in measure if and only if (A_n,δ) → 0 as n → ∞ for any positive δ. Moreover, the following are equivalent:

(i) X_n → X -a.e.

(ii) (lim sup_n A_n,0) = 0.

(iii) (lim sup_n A_n,δ) = 0 for any δ > 0.

Proof. By definition, X_n → X -a.e. if and only if (E₀) = 0. For any δ ≥ 0, E_δ ⊂ E₀ = ∪_{δ >0} E_δ, hence (E₀) = 0 if and only if (E_δ) = 0 for any δ > 0. The claim follows from (B.34).

Convergence in measure and almost everywhere convergence are not equivalent, see Example 4.76. Nevertheless, the two convergences are related, as the following proposition shows.

Proposition B.49 Let (, ) be a measure on Ω and let and X be -measurable functions on Ω. Then:

(i) If X_n → X -a.e., then X_n → X in measure.

(ii) If X_n → X in measure, then there exists a subsequence of such that X_kn → X -a.e.

Proof. (i) Let δ > 0. For any n let . By Proposition B.48, for any δ > 0. Let m ≥ 1 and define . Then A_n,δ ⊂ B_m ∀n ≥ m hence

(ii) Let . We must show that there exists a sequence n_j such that

see Definition 4.75 and (B.34). Let . By assumption (A_n,δ) → 0 for any δ > 0. Let n₁ be the smallest integer such that , and for any k ≥ 2, let n_k+1 be the smallest integer greater than n_k such that . Let . Since B_m ↓ ∩_mB_m = lim sup_j(A_nj,1/j) we obtain

Since

the claim follows.

B.4.2   Strong convergence

We see here some different results related to the Beppo Levi theorem and the convergence of integrals.

The first result is about the convergence of integrals of series of non-negative functions.

Proposition B.50 (Series of non-negative functions) Let (, ) be a measure on Ω. Let be a sequence of -measurable non-negative functions. Then

Proof. The partial sums are a nondecreasing sequence of -measurable non-negative functions. Applying the Beppo Levi theorem to this sequence yields the result.

B.4.3   Fatou lemma

In the following lemma, the monotonicity assumption in the Beppo Levi theorem is removed.

Lemma B.51 (Fatou) Let (, ) be a measure on Ω and let be a sequence of -measurable non-negative functions. Then

Proof. Let g_n(x) := inf_k≥n f_k(x). is an increasing sequence of -measurable non-negative functions. Moreover,

Thus and, applying the Beppo Levi theorem, we get

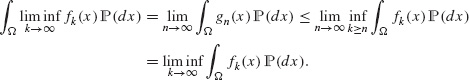
Remark B.52 The Fatou lemma implies the Beppo Levi theorem. In fact, let be an increasing sequence of functions that converges to f(x). Then f(x) = lim_k→∞ f_k(x) = lim inf_k→∞ f_k(x). Since the sequence is monotone, we get

and, by the Fatou lemma, we get the opposite inequality:

Corollary B.53 (Fatou lemma) Let (, ) be a measure on Ω. Let be a sequence of -measurable functions and let : Ω → be a -summable function.

(i) If f_k(x) ≥ (x) ∀k and -a.e. x Ω, then

(ii) If f_k(x) ≤ (x) ∀k and -a.e., then

Proof. Let and let E := ∩_k E_k. Since (E^c) = 0, we can assume without loss of generality that f_k(x) ≥ (x) ∀k and ∀x Ω. To prove (i) it suffices to apply the Fatou lemma, Lemma B.51, to the sequence . (ii) is proven similarly.

B.4.4   Dominated convergence theorem

Theorem B.54 (Lebesgue dominated convergence) Let (, ) be a measure on Ω and let be a sequence of -measurable functions. Assume:

(i) f_k(x) → f(x) -a.e. x Ω.

(ii) There exists a -summable function such that |f_k(x)| ≤ (x) ∀k and for -a.e. x.

Then

and, in particular,

Proof. By assumption |f_k(x) − f(x)| ≤ 2(x) for -a.e. x and for any k. Moreover, |f_k(x) − f(x)| → 0 ∀k and for -a.e. x. Thus, by the Fatou lemma, Corollary B.53, we get

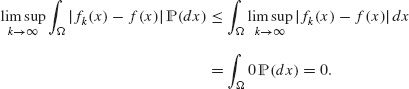
The last claim is proven by the following inequality:

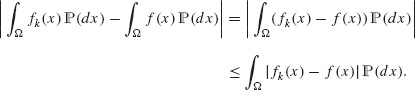
Remark B.55 Notice that in Theorem B.54:

• Assumption (ii) is equivalent to the -summability of the envelope (x) := sup_k |f_k(x)| of the functions |f_k|.
• Assumption (ii) cannot be dropped as the following sequence 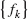shows:

  

Example B.56 The dominated convergence theorem extends to arbitrary measures a classical dominated convergence theorem for series.

Theorem (Dominated convergence for series) Let be a double sequence such that:

(i) For any j, a_j,n → a_j as n → ∞.

(ii) There exists a non-negative sequence such that |a_j,n| ≤ c_j for any n and any j and .

Then the series is absolutely convergent and

Proof. Consider the counting measure on Ω = and apply the Lebesgue dominated convergence theorem to the sequence defined by f_n(j) = a_j,n.

For the reader’s convenience, we include a direct proof. Since a_j,n → a_j and |a_n,j| ≤ c_j ∀n, j, we get |a_j| ≤ c_j ∀j so that is absolutely convergent.

Let > 0. Choose p = p() such that . Then

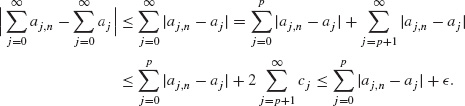
Thus, as n → ∞, we obtain

Since is arbitrary, the claim follows.

The next theorem is an important consequence on the convergence of integrals of series of functions.

Theorem B.57 (Lebesgue) Let (, ) be a measure on Ω and let be a sequence of -measurable functions such that

Then for -a.e. x the series is absolutely convergent to a -summable function f(x). Moreover,

and

Notice that the assumptions are on the integrals only, while the claim is about the -a.e. convergence of the series .

Proof. For any x Ω let be the sum of the non-negative addenda series . Applying the Beppo Levi theorem, the assumption gives

i.e. g is -summable. Thus, by Proposition B.26, g(x) < +∞ for -a.e. x, i.e. the series absolutely converges to and, for any integer p ≥ 1 we have

In particular,

so that f is summable. Integrating (B.36) we get

As p → ∞ we get the first part of the claim. The second part of the claim easily follows since

B.4.5   Absolute continuity of integrals

Theorem B.58 (Absolute continuity of integrals) Let (, ) be a measure on Ω and let f be a -summable function. For any > 0 there exists δ > 0 such that for any E such that (E) < δ. Equivalently,

Proof. Let

Then |f_k(x) − f(x)| → 0 for -a.e. x and |f_k(x) − f(x)| ≤ 2|f(x)|, Since |f| is -summable, the dominated convergence theorem, Theorem B.54, applies for any > 0 there exists such that

Let δ := /(2N). Then for any E such that (E) ≤ δ we get

so that

B.4.6   Differentiation of the integral

Let be Lebesgue-summable non-negative functions. Clearly, if and only if f(x) = g(x) almost everywhere. Thus one would like to characterize f(x) in terms of its integral, i.e. of the map . Differentiation theory provides such a characterization. Obviously, if f is continuous, then the mean value theorem gives

More generally, the following theorem holds.

Theorem B.59 (Lebesgue) Let E ⊂ be a -measurable set and let f : E → be -measurable such that for some 1 ≤ p < +∞. Then for almost every x E,

In particular, for almost every x E, the limit

exists, is finite and equal to f(x).

Example B.60 Let f be -summable on ] − 1, 1[. Show that

Definition B.61 Let be -summable on E. The points of the set

are called Lebesgue points of f. For any the limit

exists and is finite thus it defines a function called the Lebesgue representative of f.

From the Lebesgue differentiation theorem, Theorem B.59, we get

Theorem B.62 Let f be a -summable function on . Then and f = λ_f -a.e.

The differentiation theorem can be extended to more general sets than balls centred at x. One may use cubes centred at x, cubes containing x or even different objects. For example, let A be a bounded Borel set such that (A) > 0. Assume, e.g.

For any x and any r > 0, let A_x,r := x + r A. Obviously, A_x,r ⊂ B(x, 100 r) and |A_x,r| = rⁿ |A| = crⁿ |B₁| = c |B(x, r)|. Theorem B.59 implies the following.

Theorem B.63 Let E ⊂ be a Borel-measurable set and let f : E → be -measurable with for some 1 ≤ p < ∞. Then for -a.e. x E

We now collect some results due to Giuseppe Vitali (1875–1932) on the differentiation of integrals and of monotone functions.

Theorem B.64 (Vitali) Let h : → be monotone nondecreasing. Then h is differentiable at -a.e. x and the derivative h′(x) is non-negative at -a.e. x . Moreover, h′ is -summable on any bounded interval ]a, b[ and

Remark B.65 Equality may not hold in (B.37). Take, e.g. h(x) := sgn(x) so that h′(x) = 0 ∀x ≠ 0, and, of course, . Although surprising, one may construct examples of continuous and strictly increasing functions whose derivative is zero almost everywhere: one somewhat simpler example of a continuous, nonconstant and nondecreasing function with zero derivative almost everywhere is the famous Cantor–Vitali function. Obviously, for such functions the inequality in (B.37) may be strict.

Definition B.66 A function f : → is said to be absolutely continuous if for any > 0 there exists δ > 0 such that for any pair of sequences , such that we have .

Let f L¹([a, b]), Theorem B.58 implies that the integral function

is absolutely continuous. The next theorem shows that integral functions are the only absolutely continuous functions.

Theorem B.67 (Vitali) A function h : [a, b] → is absolutely continuous if and only if there exists a -summable function f on [a, b] such that

Moreover, h is differentiable at almost every x [a, b] and h′(x) = f(x) for a.e. x [a, b].

Lipschitz continuous functions f : → are absolutely continuous; thus by Theorem B.67 they are differentiable -a.e., the derivative f′(x) is -summable and

Moreover, the following holds in .

Theorem B.68 (Rademacher) Let f : → be Lipschitz continuous. Then f is differentiable at -almost every x , the map x → D f(x) is -measurable and |D f(x)| ≤ Lip(f) -a.e. x .

B.4.7   Weak convergence of measures

In this section we consider Borel measures on , that is measures ((), μ) on . Since the σ algebra is understood, we simply write μ to denote the measure ((), μ).

Recall that the law of a finite Borel measure μ on is the function F : → , F(t) := μ(] − ∞, t]). We recall that F is monotone nondecreasing, in particular, is right-continuous on and the set of its discontinuity points is at most denumerable. Moreover, F(t) → F(−∞) as t → −∞ and F(t) → F(+∞) as t → +∞ and the measure μ is completely determined by F.

Definition B.69 Let , μ be finite Borel measures on . We say that weakly converges to μ, and we write , if for any continuous bounded function φ : → one has

Proposition B.70 If the weak limit of a sequence of measures exists, then it is unique.

Proof. Assume and , and let := μ₁ – μ₂. Then, for every continuous bounded function φ: →

The characteristic function of ] − ∞, a] can be approximated from below by an increasing sequence of continuous non-negative functions, thus obtaining ([−∞, a]) = 0 ∀ , hence (A) = 0 ∀A ().

Theorem B.71 Let , μ be a finite Borel measures on . Assume μ_n() = μ() ∀n and let F_n and F be their laws, respectively. The following are equivalent:

(i) If F is continous at t, then F_n(t) → F(t).

(ii) μ_n weakly converges to μ.

Proof. (i) (ii) Without any loss of generality, we can assume that for any n , F_n(−∞) = F(−∞) = 0 and F_n(+∞) = μ_n() = μ() = F(+∞) = 1. Fix δ > 0 and let a, b , a < b, such that F is continuous at a and b, and such that F(a) ≤ δ and 1 − F(b) ≤ δ. F_n(a) and F_n(b) converge to F(a) and F(b), respectively, hence for large enough n’s, F_n(a) ≤ 2δ, 1 − F_n(b) ≤ 2δ.

Let φ : → be a bounded continuous function, |φ| ≤ M. Since φ is uniformly continuous in [a, b], there exists N = N_δ and intervals I_j = [a_j, a_j+1], j = 1, . . ., N_δ where a = a₁ < a₂ < · · · < a_N+1 = b such that the oscillation of φ on every I_j is less than δ, max_Ij φ − min_Ij φ ≤ δ∀j. Morever, perturbating the extrema a_j if necessary, we can assume that all the points a_j are continuity points for F. Let . h is a simple function h_|Ij = φ(a_j) and h = 0 in [a, b]. Moreover, |φ(x) − h(x)| ≤ δ on ]a, b]. Since φ is bounded and μ_n() = 1,

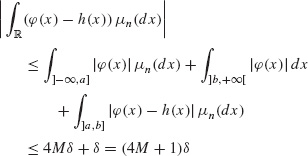
and, similarly,

hence

Since F_n(a_j) → F(a_j) for any j = 1, . . ., N, we get as n → ∞

Since δ > 0 is arbitrary, the claim is proven.

(ii) (i) Let a . It suffices to show that

In fact, from (B.38) one gets

i.e. F(a) = lim_n→∞ F_n(a) if F is continuous at a.

For any δ > 0, let φ(t) be the piecewise linear function that is null for any t ≥ a and is identically 1 for t ≤ a − δ. Then

As δ → 0⁺, F(a − δ) → F(a⁻), so the first inequality in (B.38) is proven. Similarly, let φ(t) be the piecewise linear function that is null for t ≥ a + δ and is identically 1 for t ≤ a. Then

As δ → 0⁺, F(a + δ) → F(a) so that the second inequality in (B.38) holds. The proof of (B.38) is then complete.

Let (, ) be a probability measure on a set Ω. We recall that the law F_X associated with an -measurable function X : Ω → is the law of the image measure of through X, i.e.

Definition B.72 Let (, ) be a finite measure on a set Ω and let , X be -measurable functions. We say that converges in law to X if F_Xn (t) converges to F_X(t) pointwisely in all points of continuity of F_X.

Proposition B.73 Let (, ) be a finite measure on a set Ω and let , X be -measurable functions. If X_n → X in measure then X_n converges in law to X.

Proof. If suffices to prove that

In fact, from (B.39) one gets

hence F_X(a) = lim_n→∞ F_Xn(a) if F_X is continuous at a.

Let us prove (B.39). Let δ > 0. Since

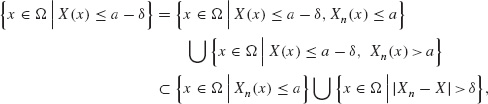
we have

Thus, passing to the limit with respect to n, we obtain

If we now let δ → 0⁺, we get the first inequality (B.39). Similarly,

so that

As n → ∞ we get

so that, by letting δ → 0⁺ we obtain the second inequality of (B.39).

B.4.8   Exercises

Exercise B.74 Let f : → be -summable. Prove that the function F : × [0, ∞[ → defined by

is continuous.

Exercise B.75 Let f L¹(). Prove that the following equalities hold for a.e. x :

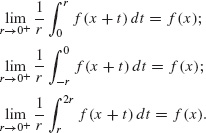
Exercise B.76 Let φ : [a, b] → [c, d] be continuous and piecewise differentiable. Let h : [c, d] → be absolutely continuous. Prove that f ○ φ : [a, b] → is absolutely continuous.

Exercise B.77 Let φ : [a, b] → [c, d] be continuous. Then φ is absolutely continuous if and only if the graph of φ has finite length.

Exercise B.78 Let (, ) be a measure on a set Ω. Let , X be -measurable functions and let p [1, ∞[. Assume that:

(i) X_n → X -a.e. x Ω.

(ii) .

Prove that .

Solution. For any positive n the function Y_n := 2^p−1(|X|^p + |X_n|^p) − |X_n − X|^p is non-negative. Moreover, as n → ∞, Y_n converges to 2^p|X|^p -a.e. Thus, by the Fatou lemma