Appendix B
FINANCIAL MARKETS ARITHMETIC
Simple interest
A loan that has one interest payment on maturity is accruing simple interest. On short-term instruments there is usually only the one interest payment on maturity, hence simple interest is received when the instrument expires. The terminal value of an investment with simple interest is given by:
where
![]()
So, for example, if PV is 100, is 5% and the investment is 1 year. Then
![]()
The market convention is to quote interest rates as annualized interest rates, which is the interest that is earned if the investment term is 1 year. Consider a 3-month deposit of 100 in a bank, placed at a rate of interest of 6%. In such an example the bank deposit will earn 6% interest for a period of 90 days. As the annual interest gain would be 6, the investor will expect to receive a proportion of this:
![]()
So, the investor will receive 1.479 interest at the end of the term. The total proceeds after the 3 months is therefore 100 plus 1.479. If we wish to calculate the terminal value of a short-term investment that is accruing simple interest we use the following expression:
(B.2) ![]()
The fraction ![]() refers to the numerator, which is the number of days the investment runs, divided by the denominator, which is the number of days in the year. In sterling markets the number of days in a year is taken to be 365; however, certain other markets (including euro currency markets) have a 360-day year convention. For this reason we simply quote the expression as ‘days’ divided by ‘year’ to allow for either convention.
refers to the numerator, which is the number of days the investment runs, divided by the denominator, which is the number of days in the year. In sterling markets the number of days in a year is taken to be 365; however, certain other markets (including euro currency markets) have a 360-day year convention. For this reason we simply quote the expression as ‘days’ divided by ‘year’ to allow for either convention.
Compound interest
Let us now consider an investment of 100 made for 3 years, again at a rate of 6%, but this time fixed for 3 years. At the end of the first year the investor will be credited with interest of 6. Therefore, for the second year the interest rate of 6% will be accruing on a principal sum of 106, which means that at the end of Year 2 the interest credited will be 6.36. This illustrates how compounding works, which is the principle of earning interest on interest. What will the terminal value of our 100 3-year investment be?
In compounding we are seeking to find a future value given a present value, a time period and an interest rate. If 100 is invested today (at time ) at 6%, then 1 year later () the investor will have. In our example the capital is left in for another 2 years, so at the end of Year 2 () we will have:
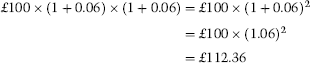
The outcome of the process of compounding is the future value of the initial amount. We don’t have to calculate the terminal value long hand as we can use:
(B.3) ![]()
where
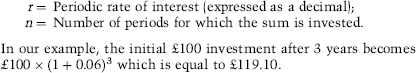
In our example, the initial 100 investment after 3 years becomes which is equal to 119.10.
When we compound interest we have to assume that the reinvestment of interest payments during the investment term is at the same rate as the first year’s interest. That is why we stated that the 6% rate in our example was fixed for 3 years. However, we can see that compounding increases our returns compared with investments that accrue only on a simple interest basis. If we had invested 100 for 3 years fixed at a rate of 6% but paying on a simple interest basis our terminal value would be 118, which is 1.10 less than our terminal value using a compound interest basis.
Compounding more than once a year
Now let us consider a deposit of 100 for 1 year, again at our rate of 6% but with quarterly interest payments. Such a deposit would accrue interest of 6 in the normal way, but 1.50 would be credited to the account every quarter, and this would then benefit from compounding. Again assuming that we can reinvest at the same rate of 6%, the total return at the end of the year will be:
![]()
which gives us, a terminal value of 106.136. This is some 13 pence more than the terminal value using annual compounded interest.
In general, if compounding takes place times per year, then at the end of years interest payments will have been made and the future value of the principal is given by:
As we showed in our example, the effect of more frequent compounding is to increase the value of total return when compared with annual compounding. The effect of more frequent compounding is shown below, where we consider annualized interest rate factors, for an annualized rate of 5%.

This shows us that the more frequent the compounding the higher the interest rate factor. The last case also illustrates how a limit occurs when interest is compounded continuously. Equation (B.4) can be rewritten as:
where. As compounding becomes continuous and and hence approach infinity, equation (B.5) approaches a value known as, which is shown by:
If we substitute this into (B.5) we get:
![]()
where we have continuous compounding. In equation (B.6) is known as the exponential function of ; it tells us the continuously compounded interest rate factor. If % and year then:
![]()
This is the limit reached with continuous compounding. To illustrate continuous compounding from our initial example, the future value of 100 at the end of 3 years – when the interest rate is 6% – can be given by:
![]()
Effective interest rates
The interest rate quoted on a deposit or loan is usually the flat rate. However, we are often required to compare two interest rates which apply for a similar investment period but have different interest payment frequencies – for example, a 2-year interest rate with interest paid quarterly compared with a 2-year rate with semi-annual interest payments. This is normally done by comparing equivalent annualized rates. The annualized rate is the interest rate with annual compounding that results in the same return at the end of the period as the rate we are comparing.
The concept of the effective interest rate allows us to state that:
(B.7) ![]()
where AER is the equivalent annual rate. Therefore, if is the interest rate quoted that pays interest payments per year, AER is given by:
The equivalent annual interest rate AER is known as the effective interest rate. We have already referred to the quoted interest rate as the ‘nominal’ interest rate. We can rearrange equation (B.8) to give us equation (B.9) which allows us to calculate nominal rates:
We can see then that the effective rate will be greater than the flat rate if compounding takes place more than once a year. The effective rate is sometimes referred to as the annualized percentage rate or APR.
Interest rate conventions
The convention in both wholesale or personal (retail) markets is to quote an annual interest rate. A lender who wishes to earn interest at the rate quoted has to place her funds on deposit for 1 year. Annual rates are quoted irrespective of the maturity of a deposit, from overnight to 10 years or longer. For example, if one opens a bank account that pays interest at a rate of 3.5% but then closes it after 6 months, the actual interest earned will be equal to 1.75% of the sum deposited. The actual return on a 3-year building society bond (fixed deposit) that pays 6.75% fixed for 3 years is 21.65% after 3 years. The quoted rate is the annual 1-year equivalent. An overnight deposit in the wholesale or inter-bank market is still quoted as an annual rate, even though interest is earned for only one day.
The convention of quoting annualized rates is to allow deposits and loans of different maturities and different instruments to be compared on the basis of the interest rate applicable. We must also be careful when comparing interest rates for products that have different payment frequencies. As we have seen from the foregoing paragraphs the actual interest earned will be greater for a deposit earning 6% on a semi-annual basis compared with 6% on an annual basis. The convention in the money markets is to quote the equivalent interest rate applicable when taking into account an instrument’s payment frequency.
Discount factors
The calculation of present values from future values is also known as discounting. The principles of present and future values demonstrate the concept of the time value of money which is that in an environment of positive interest rates a sum of money has greater value today than it does at some point in the future because we are able to invest the sum today and earn interest. We will only consider a sum in the future compared with a sum today if we are compensated by being paid interest at a sufficient rate. Discounting future values allows us to compare the value of a future sum with a present sum.
The rate of interest, known as the discount rate, is the rate we use to discount a known future value in order to calculate a present value. We can rearrange equation (B.1) to give:
![]()
The term is known as the -year discount factor:
(B.10) ![]()
where is the -year discount factor.
The 3-year discount factor when the discount rate is 9% is:
![]()
We can calculate discount factors for all possible interest rates and time periods to give us a discount function. Fortunately, we don’t need to calculate discount factors ourselves as this has been done for us (discount tables for a range of rates are provided in Table B.1).
Table B.1 Discount Factor Table


Formula summary
Discount factor with simple interest ![]()
Discount factor with compound interest ![]()
Earlier we established the continuously compounded interest rate factor as. Therefore, using a continuously compounded interest rate we can establish the discount factor to be:
(B.11) 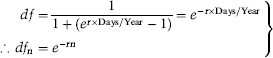
The continuously compounded discount factor is part of the formula used in option-pricing models. It is possible to calculate discount factors from the prices of government bonds. The traditional approach described in most textbooks requires that we first use the price of a bond that has only one remaining coupon, its last one, and calculate a discount factor from this bond’s price. We then use this discount factor to calculate the discount factors of bonds with ever-increasing maturities, until we obtain the complete discount function.
Present values with multiple discounting
Present values for short-term investments of under 1-year maturity often involve a single interest payment. If there is more than one interest payment then any discounting needs to take this into account. If discounting takes place times per year then we can use equation (B.4) to derive the present value formula:
For example, what is the present value of the sum of 1,000 which is to be received in 5 years where the discount rate is 5% and there is semi-annual discounting?
Using equation (B.12) we see that
![]()
The effect of more frequent discounting is to lower the present value. As with continuous compounding, the limiting factor is reached by means of continuous discounting. We can use equation (B.6) to derive the present value formula for continuous discounting
(B.13) ![]()
If we consider the same example as before but now with continuous discounting, we can use this expression to calculate the present value of 1,000 to be received in 5 years’ time as:
![]()
MULTIPLE CASHFLOWS
Future values
Up to now we have considered the future values of a single cashflow. Of course, the same principles of the time value of money can be applied to a bundle of cashflows. A series of cashflows can be at regular or at irregular intervals. If we wish to calculate the total future value of a set of irregular payments made in the future we need to calculate each payment separately and then sum all the cashflows. The formula is represented as:
where is the payment in year ; and the symbol means ‘the sum of’. We assume that payment is made and interest credited at the end of each year.
It is much more common to come across a regular stream of future payments. Such a cashflow is known as an annuity. In an annuity the payments are identical and so – as given in equation (B.14) – simply becomes. We can then rearrange equation (B.14) as:
This equation can be simplified to give us:1
This formula can be used to calculate the future value of an annuity. For example, if we consider an annuity that pays 500 each year for 10 years at a rate of 6%, its future value is given by:
![]()
The common definition of an annuity is a continuous stream of cashflows. In practice, the pension represented by an annuity is usually paid in monthly instalments, similar to an employed person’s annual salary. Certain regular payments compound interest on a more frequent basis than annually, so equation (B.15) needs to be adjusted slightly. If compounding occurs times each year, then equation (B.15) needs to be altered to equation (B.17) to allow for this:
To make calculations simpler we can multiply both sides of equation (B.17) by and subtract the result from equation (B.17). Simplifying this will then result in:
For example, a 10-year annuity that has annual payments of 5,000, but compounded on a quarterly basis at a rate of 5%, will have a future value of 63,073 as:
![]()
Where there is continuous compounding, as before the limiting factor will result in equation (B.23) becoming:
Equations (B.18) and (B.19) can be adjusted yet again to allow for frequent payments together with frequent compounding, but such a stream of cashflows is rarely encountered in practice. In the case of continuous compounding of continuous payments, the limiting factor expression is:
(B.20) ![]()
Present values
Using similar principles to those employed for calculating future values, we can calculate present values for a stream of multiple cashflows. The method employed is slightly different according to whether cashflows are regular or irregular.
For irregular payments we calculate present value by applying the conventional present value formula to each separate cashflow and then summing the present values. This is represented by:
(B.21) ![]()
where is the cashflow made in Year.
Consider a series of annual cash payments made up of 100 in the first year and then increasing by 100 each year until the fifth year. The present value of this cashflow stream is:
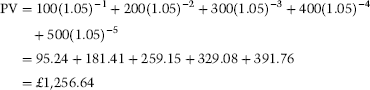
The more frequently encountered type of cashflow stream is an annuity, regular annual payments with annual discounting. To calculate the present value of an annuity we can use a variation of equation (B.16):
(B.22) 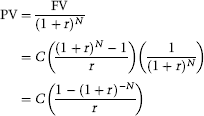
Consider now an annuity paying 5,000 each year for 20 years at an interest rate 4.5%. The present value of this annuity is:
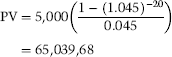
We illustrate this principle using a 20-year annuity that employs annual discounting. If a cashflow stream employs more frequent discounting we need to adjust the formula again. If an annuity discounts its cashflows times each year then the present value of its cashflow stream is found using the present-value-adjusted equation – that is, equation (B.18). This becomes:
If continuous discounting is employed then this results once again in the limiting factor for continuous discounting, so we adjust equation (B.23) and the new expression is:
(B.24) ![]()
The last case to consider is that of the payments stream that has more frequent cashflows in addition to more frequent discounting. Such a payments stream will have cashflows each year which are also discounted times per year. To calculate the present value of the cashflows we use:
The limiting factor for continuous discounting of continuous payments is:
(B.26) ![]()
Payment streams that have cashflow frequencies greater than annually or semi-annually occur quite often in the markets. To illustrate how we might use equation (B.25), consider a mortgage-type loan taken out at the beginning of a period. If the borrower is able to fix the interest rate being charged to the whole life of the mortgage, she can calculate the size of monthly payments required to pay off the loan at the end of the period.
For example, consider a repayment mortgage of 76,000 taken out for 25 years at a fixed rate of interest of 6.99%. The monthly repayments that would be charged can be calculated using equation (B.25) as:
(B.27) ![]()
where is the size of the monthly payment. Substituting the terms of the mortgage payments into the equation we obtain:
![]()
The monthly repayment is therefore 536.67 and includes interest chargeable in addition to repayment of some of the principal (hence the term repayment mortgage, as opposed to endowment mortgage which only pays off the monthly interest charge). A repayment mortgage is also known as an amortized mortgage. An amortized loan is one where a proportion of the original loan capital is paid off each year. Loans that require the borrower to service the interest charge once a year are known as straight or bullet loans. It is for this reason that plain vanilla bonds are sometimes known as bullet bonds, since the capital element of a loan raised through a vanilla bond issue is repaid only on maturity.
Perpetual cashflows
The type of annuity that we as individuals are most familiar with is the annuity pension, purchased from a life assurance company using the proceeds of a pension fund at the time of retirement. Such an annuity pays a fixed annual cash amount for an undetermined period, usually until the death of the beneficiary. An annuity with no set finish date is known as a perpetuity. As the end date of a perpetuity is unknown we are not able to calculate its present value with certainty; however, a characteristic of the term is that it approaches zero as tends to infinity. This fact reduces our present value expression to:
We can use this formula to approximate the present value of a perpetuity.
The UK gilt market includes four gilts that have no redemption date – so-called undated bonds. The largest issue amongst undated gilts is the 3% war loan, a stock originally issued at the time of the 1914–1918 war. This bond pays a coupon of ![]() per 100 nominal of stock. Since the cashflow structure of this bond matches a perpetual, its present value – using equation (B.28) when long-dated market interest rates are at, say, 5% – would be:
per 100 nominal of stock. Since the cashflow structure of this bond matches a perpetual, its present value – using equation (B.28) when long-dated market interest rates are at, say, 5% – would be:
![]()
The present value of the cashflow stream represented by the war loan stock when market rates are 5% would therefore be 70 per 100 nominal of stock. In fact, because this bond pays coupon on a semi-annual basis we should adjust the calculation to account for the more frequent payment of coupons and discounting, so the present value (price) of the bond is more accurately described as:
![]()
although – as we would expect – this still gives us a price of 70 per 100 nominal!
Corporate finance project appraisal
Two common techniques used by corporates and governments to evaluate whether a project is worth undertaking are net present value and internal rate of return. Both techniques evaluate the anticipated cashflows associated with a project, using the discounting and present value methods described in this chapter. Generally speaking, it is a company’s cost of capital that is used as the discount rate in project appraisal, and most companies attempt to ascertain the true cost of their capital as accurately as possible. As most corporate financing is usually a complex mixture of debt and equity this is sometimes problematic.
Net present value
In the case of an investment of funds made as part of a project, we would have a series of cashflows – some of which would be positive and others negative. In the early stages of a project we would typically forecast negative cashflows as a result of investment outflows, followed by positive cashflows as the project began to show a return. Each cashflow can be present-valued in the usual way. In project appraisal we would seek to find the present value of the entire stream of cashflows; the sum of all positive and negative present values added together is the net present value (NPV). As the appraisal process takes place before the project is undertaken, the future cashflows that we are concerned with will be estimated forecasts and may not actually be received once the project is under way.
The net present value equation is used to show that:
(B.29) ![]()
where is the cashflow used for the project during period. The rate used to discount cashflows can be the company’s cost of capital or the rate of return required by the company to make the project viable.
Companies will apply NPV analysis to expected projected returns because funds invested in any undertaking have a time-related cost – the opportunity cost that is the corporate cost of capital. In effect, NPV measures the present value of the gain achieved from investing in the project (provided that it is successful!). The general rule of thumb applied is that any project with a positive NPV is worthwhile, whereas those with a negative NPV, discounted at the required rate of return or the cost of capital, should be avoided.
Example B.1
What is the NPV of the following set of expected cashflows, discounted at a rate of 15%?
| Year 0 | 23,000 |
| Year 1 | 8,000 |
| Year 2 | 8,000 |
| Year 3 | 8,000 |
| Year 4 | 11,000 |
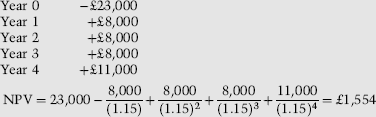
The internal rate of return
The internal rate of return (IRR) for an investment is the discount rate that equates the present value of expected cashflows (the NPV) to zero. Using the present value expression we can represent it by rate such that:
where
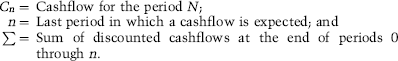
If the initial cashflow occurs at time 0, equation (B.30) can be expressed as:
(B.31) ![]()
In corporate finance project appraisal, is a cash outflow and to are cash inflows. Thus, is the rate that discounts the stream of future cashflows ( through ) to equal the initial outlay at time 0. We must therefore assume that the cashflows received are subsequently reinvested to realize the same rate of return as. Solving for the internal rate of return, cannot be found analytically and has to be found either through numerical iteration or using a computer or programmable calculator.
To illustrate the IRR consider the project cashflows given in Example B.1. If we wish to find the IRR long hand then we would have to obtain the NPV using different discount rates until we found the rate that gave an NPV equal to zero. The quickest way to do this manually is to select two discount rates, one giving a negative NPV and the other a positive NPV, and then interpolate between them. This method of solving for IRR is known as an iterative process and involves converging on a solution through trial and error. This is in fact the only way to calculate the IRR for a set of cashflows; it matches exactly the iterative process that a computer uses (the computer is just a touch quicker!). If we have two discount rates – say, and that give positive and negative NPVs, respectively, for a set of cashflows – the IRR can be estimated using:
(B.32) 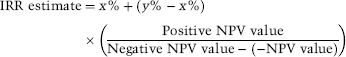
Example B.2
Using a discount rate of 15% produced a positive NPV in Example B.1. Discounting the cashflows at 19% produces an NPV of. Therefore, the estimate for IRR is:
![]()
The IRR is approximately 18.19%. This can be checked using a programmable calculator or spreadsheet programme; it may also be checked manually by calculating the NPV of the original cashflows using a discount rate of 18.19% – it should come to. We obtain an IRR of 18.14% using a calculator.
The relationship between the IRR and the NPV of an investment can be summed up as follows: while the NPV is the value of projected returns from the investment using an appropriate discount rate (usually the company’s cost of capital), the IRR is the discount rate which results in the NPV being zero. For this reason it is common to hear the IRR referred to as a project’s breakeven rate. A conventional investment is considered attractive if the IRR exceeds a company’s cost of capital and the NPV is positive. In the context of bond markets, as long as the discount rate applicable does indeed remain constant for the reinvestment of all cashflows arising from a financial instrument, the IRR can then be assumed to be the yield to maturity for that instrument. Yield to maturity is the main measure of the rate of return achieved from holding a bond.
Interpolation and extrapolation
Interest rates in the money markets are always quoted for standard maturities: for example, overnight, ‘tom next’ (the overnight interest rate starting tomorrow, or ‘tomorrow to the next’), spot next (the overnight rate starting 2 days forward), 1 week, 1 month, 2 months and so on up to 1 year. Figure B.1 shows a typical brokers’ screen as seen on news services such as Reuters and Telerate.
If a bank or corporate customer wishes to deal for non-standard periods, an inter-bank desk will calculate the rate chargeable for such an ‘odd date’ by interpolating between two standard period interest rates. If we assume that the rate for all dates in between two periods increases at the same pace, we can calculate the required rate using the formula for straight line interpolation:
(B.33) ![]()
where
![]()
Figure B.1 A typical brokers’ screen.