Chapter 3: Regular Languages and Regular Grammars

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

CHAPTER 3

REGULAR LANGUAGES AND REGULAR GRAMMARS

CHAPTER SUMMARY

In this chapter, we explore two alternative methods for describing regular languages: regular expressions and regular grammars.

Regular expressions, whose form is reminiscent of the familiar arithmetic expressions, are convenient in some applications because of their simple string form, but they are restricted and have no obvious extension to the more complicated languages we will encounter later. Regular grammars, on the other hand, are just a special case of many different types of grammars.

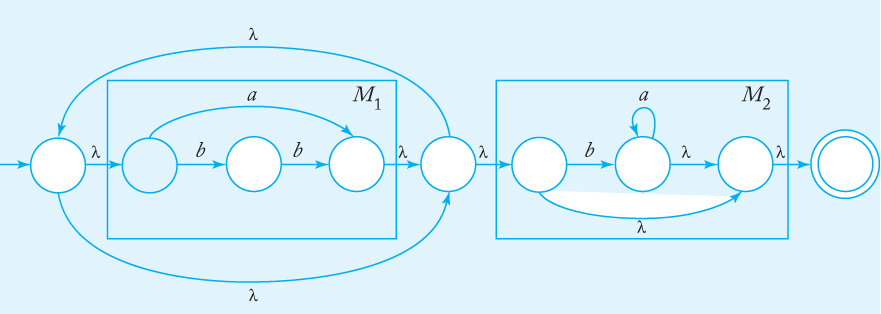
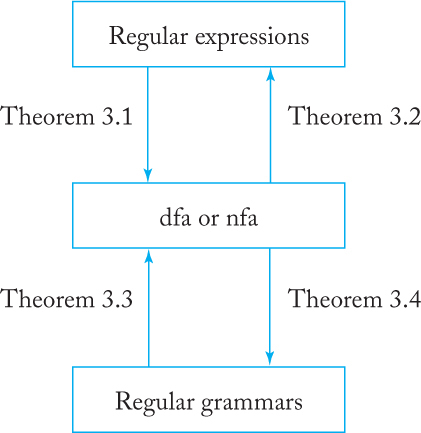
The purpose of this chapter is to explore the essential equivalence of these three modes of describing regular languages. The constructions that make conversion from one form to another are in the theorems in this chapter. Their relation is illustrated in Figure 3.19.

Since each representation of a regular language is fully convertible to any of the others, we can choose whichever is most convenient for the situation at hand. Remembering this will often simplify your work.

According to our definition, a language is regular if there exists a finite accepter for it. Therefore, every regular language can be described by some dfa or some nfa. Such a description can be very useful, for example, if we want to show the logic by which we decide if a given string is in a certain language. But in many instances, we need more concise ways of describing regular languages. In this chapter, we look at other ways of representing regular languages. These representations have important practical applications, a matter that is touched on in some of the examples and exercises.

3.1 REGULAR EXPRESSIONS

One way of describing regular languages is via the notation of regular expressions. This notation involves a combination of strings of symbols from some alphabet Σ, parentheses, and the operators +, ·, and ∗. The simplest case is the language {a}, which will be denoted by the regular expression a. Slightly more complicated is the language {a, b, c}, for which, using the + to denote union, we have the regular expression a + b + c. We use · for concatenation and ∗ for star-closure in a similar way. The expression (a + (b · c))* stands for the star-closure of {a}∪{bc}, that is, the language {λ, a, bc, aa, abc, bca, bcbc, aaa, aabc, ...}.

Formal Definition of a Regular Expression

We construct regular expressions from primitive constituents by repeatedly applying certain recursive rules. This is similar to the way we construct familiar arithmetic expressions.

DEFINITION 3.1

Let Σ be a given alphabet. Then

1. ∅, λ, and a ∈ Σ are all regular expressions. These are called primitive regular expressions.

2. If r₁ and r₂ are regular expressions, so are r₁ + r₂, r₁ · r₂, $r_{1}^{*}$ $r_{1}^{*}$ , and (r₁).

3. A string is a regular expression if and only if it can be derived from the primitive regular expressions by a finite number of applications of the rules in (2).

EXAMPLE 3.1

For Σ = {a, b, c}, the string

(a + b · c)* · (c + ∅)

is a regular expression, since it is constructed by application of the above rules. For example, if we take r₁ = c and r₂ = ∅, we find that c + ∅ and (c + ∅) are also regular expressions. Repeating this, we eventually generate the whole string. On the other hand, (a + b +) is not a regular expression, since there is no way it can be constructed from the primitive regular expressions.

Languages Associated with Regular Expressions

Regular expressions can be used to describe some simple languages. If r is a regular expression, we will let L (r) denote the language associated with r.

DEFINITION 3.2

The language L (r) denoted by any regular expression r is defined by the following rules.

1. ∅ is a regular expression denoting the empty set,

2. λ is a regular expression denoting {λ},

3. For every a ∈ Σ, a is a regular expression denoting {a}.

If r₁ and r₂ are regular expressions, then

4. L (r₁ + r₂) = L (r₁) ∪ L (r₂),

5. L (r₁ · r₂) = L (r₁) L (r₂),

6. L ((r₁)) = L (r₁),

7. L ( $r_{1}^{*}$ $r_{1}^{*}$ ) = (L (r₁))*.

The last four rules of this definition are used to reduce L (r) to simpler components recursively; the first three are the termination conditions for this recursion. To see what language a given expression denotes, we apply these rules repeatedly.

EXAMPLE 3.2

Exhibit the language L (a* · (a + b)) in set notation.

L (a* · (a + b))	=	L (a*) L (a + b)
	=	(L (a))* (L (a) ∪ L (b))
	=	{λ, a, aa, aaa, ...}{a, b}
	=	{a, aa, aaa, ..., b, ab, aab, ...}.

There is one problem with rules (4) to (7) in Definition 3.2. They define a language precisely if r₁ and r₂ are given, but there may be some ambiguity in breaking a complicated expression into parts. Consider, for example, the regular expression a · b + c. We can consider this as being made up of r₁ = a · b and r₂ = c. In this case, we find L (a · b + c) = {ab, c}. But there is nothing in Definition 3.2 to stop us from taking r₁ = a and r₂ = b + c. We now get a different result, L (a · b + c) = {ab, ac}. To overcome this, we could require that all expressions be fully parenthesized, but this gives cumbersome results. Instead, we use a convention familiar from mathematics and programming languages. We establish a set of precedence rules for evaluation in which star-closure precedes concatenation and concatenation precedes union. Also, the symbol for concatenation may be omitted, so we can write r₁r₂ for r₁ · r₂.

With a little practice, we can see quickly what language a particular regular expression denotes.

EXAMPLE 3.3

For Σ = {a, b}, the expression

r = (a + b)* (a + bb)

is regular. It denotes the language

L (r) = {a, bb, aa, abb, ba, bbb, ...}.

We can see this by considering the various parts of r. The first part, (a + b)*, stands for any string of a’s and b’s. The second part, (a + bb) represents either an a or a double b. Consequently, L (r) is the set of all strings on {a, b}, terminated by either an a or a bb.

EXAMPLE 3.4

The expression

r = (aa)* (bb)* b

denotes the set of all strings with an even number of a’s followed by an odd number of b’s; that is,

L (r) = {a²ⁿb^2m+1 : n ≥ 0, m ≥ 0}.

Going from an informal description or set notation to a regular expression tends to be a little harder.

EXAMPLE 3.5

For Σ = {0, 1}, give a regular expression r such that

L (r) = {w ∈ Σ* : w has at least one pair of consecutive zeros}.

One can arrive at an answer by reasoning something like this: Every string in L (r) must contain 00 somewhere, but what comes before and what goes after is completely arbitrary. An arbitrary string on {0, 1} can be denoted by (0 + 1)*. Putting these observations together, we arrive at the solution

r = (0 + 1)* 00 (0 + 1)*.

EXAMPLE 3.6

Find a regular expression for the language

L = {w ∈ {0, 1}* : w has no pair of consecutive zeros}.

Even though this looks similar to Example 3.5, the answer is harder to construct. One helpful observation is that whenever a 0 occurs, it must be followed immediately by a 1. Such a substring may be preceded and followed by an arbitrary number of 1’s. This suggests that the answer involves the repetition of strings of the form 1 ··· 101 ··· 1, that is, the language denoted by the regular expression (1*011*)*. However, the answer is still incomplete, since the strings ending in 0 or consisting of all 1’s are unaccounted for. After taking care of these special cases we arrive at the answer

r = (1*011*)* (0 + λ) + 1* (0 + λ).

If we reason slightly differently, we might come up with another answer. If we see L as the repetition of the strings 1 and 01, the shorter expression

r = (1 + 01)* (0 + λ)

might be reached. Although the two expressions look different, both answers are correct, as they denote the same language. Generally, there are an unlimited number of regular expressions for any given language.

Note that this language is the complement of the language in Example 3.5. However, the regular expressions are not very similar and do not suggest clearly the close relationship between the languages.

The last example introduces the notion of equivalence of regular expressions. We say the two regular expressions are equivalent if they denote the same language. One can derive a variety of rules for simplifying regular expressions (see Exercise 20 in the following exercise section), but since we have little need for such manipulations we will not pursue this.

EXERCISES

1. Find all strings in L ((a + bb)^∗) of length five.

2. Find all strings in L ((ab + b)^∗ b (a + ab)^∗) of length less than four.

3. Find an nfa that accepts the language L (aa^∗ (ab + b)).

4. Find an nfa that accepts the language L (aa^∗ (a + b)).

5. Does the expression ((0 + 1) (0 + 1)^∗)^∗ 00 (0 + 1)^∗ denote the language in Example 3.5?

6. Show that r = (1 + 01)^∗ (0+1^∗) also denotes the language in Example 3.6. Find two other equivalent expressions.

7. Find a regular expression for the set {aⁿb^m : n ≥ 3, m is odd}.

8. Find a regular expression for the set {aⁿb^m : (n + m) is odd}.

9. Give regular expressions for the following languages.

(a) L₁ = {aⁿb^m, n ≥ 3, m ≤ 4}.

(b) L₂ = {aⁿb^m : n < 4, m ≤ 4}.

(d) The complement of L₂.

10. What languages do the expressions (⊘^∗)^∗ and a ⊘ denote?

11. Give a simple verbal description of the language L ((aa)^∗ b (aa)^∗ + a (aa)^∗ ba (aa)^∗).

12. Give a regular expression for L^R, where L is the language in Exercise 2.

13. Give a regular expression for L = {aⁿb^m : n ≥ 2, m ≥ 1, nm ≥ 3}.

14. Find a regular expression for L = {abⁿw : n ≥ 4, w ∈ {a, b}⁺}.

15. Find a regular expression for the complement of the language in Example 3.4.

16. Find a regular expression for L = {vwv : v, w ∈ {a, b}^∗, |v| = 2}.

17. Find a regular expression for L = {vwv : v, w ∈ {a, b}^∗, |v| ≤ 4}.

18. Find a regular expression for

L = {w ∈ {0, 1}^∗ : w has exactly one pair of consecutive zeros}.

19. Give regular expressions for the following languages on Σ = {a, b, c}:

(a) All strings containing exactly two a’s.

(b) All strings containing no more than three a’s.

20. Write regular expressions for the following languages on {0, 1}:

(a) All strings ending in 10.

(b) All strings not ending in 10.

21. Find regular expressions for the following languages on {a, b}:

(a) L = {w : |w| mod 3 ≠ 0}.

(b) L = {w : n_a (w) mod 3 = 0}.

22. Determine whether or not the following claims are true for all regular expressions r₁ and r₂. The symbol ≡ stands for equivalence of regular expressions in the sense that both expressions denote the same language.

(a) ${(r_{1}^{*})}^{*} \equiv r_{1}^{*}$ ${(r_{1}^{*})}^{*} \equiv r_{1}^{*}$

(b) ${r_{1}^{*} (r_{1} + r_{2})}^{*} \equiv {(r_{1} + r_{2})}^{*}$ ${r_{1}^{*} (r_{1} + r_{2})}^{*} \equiv {(r_{1} + r_{2})}^{*}$

(c) ${(r_{1} + r_{2})}^{*} \equiv {(r_{1}^{*} + r_{2}^{*})}^{*}$ ${(r_{1} + r_{2})}^{*} \equiv {(r_{1}^{*} + r_{2}^{*})}^{*}$

(d) ${(r_{1} r_{2})}^{*} \equiv r_{1}^{*} r_{2}^{*}$ ${(r_{1} r_{2})}^{*} \equiv r_{1}^{*} r_{2}^{*}$

23. Give a general method by which any regular expression r can be changed into $\hat{r}$ $\hat{r}$ such that ${(L (r))}^{R} = L (\hat{r})$ ${(L (r))}^{R} = L (\hat{r})$ .

24. Prove rigorously that the expressions in Example 3.6 do indeed denote the specified language.

25. For the case of a regular expression r that does not involve λ or ⊘, give a set of necessary and sufficient conditions that r must satisfy if L (r) is to be infinite.

26. Formal languages can be used to describe a variety of two-dimensional figures. Chain-code languages are defined on the alphabet Σ = {u, d, r, l}, where these symbols stand for unit-length straight lines in the directions up, down, right, and left, respectively. An example of this notation is urdl, which stands for the square with sides of unit length. Draw pictures of the figures denoted by the expressions (rd)^∗, (urddru)^∗, and (ruldr)^∗.

27. In Exercise 27, what are sufficient conditions on the expression so that the picture is a closed contour in the sense that the beginning and ending points are the same? Are these conditions also necessary?

28. Find a regular expression that denotes all bit strings whose value, when interpreted as a binary integer, is greater than or equal to 40.

29. Find a regular expression for all bit strings, with leading bit 1, interpreted as a binary integer, with values not between 10 and 30.

3.2 CONNECTION BETWEEN REGULAR EXPRESSIONS AND REGULAR LANGUAGES

As the terminology suggests, the connection between regular languages and regular expressions is a close one. The two concepts are essentially the same; for every regular language there is a regular expression, and for every regular expression there is a regular language. We will show this in two parts.

Regular Expressions Denote Regular Languages

We first show that if r is a regular expression, then L (r) is a regular language. Our definition says that a language is regular if it is accepted by some dfa. Because of the equivalence of nfa’s and dfa’s, a language is also regular if it is accepted by some nfa. We now show that if we have any regular expression r, we can construct an nfa that accepts L (r). The construction for this relies on the recursive definition for L (r). We first construct simple automata for parts (1), (2), and (3) of Definition 3.2, then show how they can be combined to implement the more complicated parts (4), (5), and (7).

THEOREM 3.1

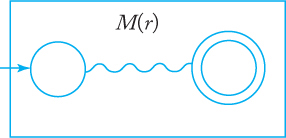
Let r be a regular expression. Then there exists some nondeterministic finite accepter that accepts L (r). Consequently, L (r) is a regular language.

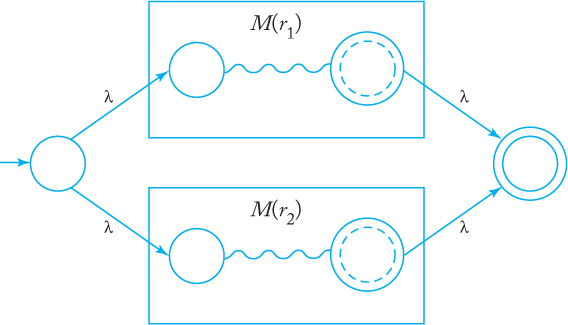
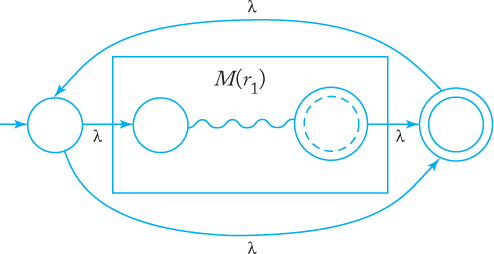
Proof: We begin with automata that accept the languages for the simple regular expressions ∅, λ, and a ∈ Σ. These are shown in Figure 3.1(a), (b), and (c), respectively. Assume now that we have automata M (r₁) and M (r₂) that accept languages denoted by regular expressions r₁ and r₂, respectively. We need not explicitly construct these automata, but may represent them schematically, as in Figure 3.2. In this scheme, the graph vertex at the left represents the initial state, the one on the right the final state. In Exercise 7, Section 2.3, we claim that for every nfa there is an equivalent one with a single final state, so we lose nothing in assuming that there is only one final state. With M (r₁) and M (r₂) represented in this way, we then construct automata for the regular expressions r₁ + r₂, r₁r₂, and $r_{1}^{*}$ $r_{1}^{*}$ . The constructions are shown in Figures 3.3 to 3.5. As indicated in the drawings, the initial and final states of the constituent machines lose their status and are replaced by new initial and final states. By stringing together several such steps, we can build automata for arbitrary complex regular expressions.

FIGURE 3.1 (a) nfa accepts ∅. (b) nfa accepts {λ}. (c) nfa accepts {a}.

FIGURE 3.2 Schematic representation of an nfa accepting L (r).

It should be clear from the interpretation of the graphs in Figures 3.3 to 3.5 that this construction works. To argue more rigorously, we can give a formal method for constructing the states and transitions of the combined machine from the states and transitions of the parts, then prove by induction on the number of operators that the construction yields an automaton that accepts the language denoted by any particular regular expression. We will not belabor this point, as it is reasonably obvious that the results are always correct.

FIGURE 3.3 Automaton for L (r₁ + r₂).

FIGURE 3.4 Automaton for L (r₁r₂).

FIGURE 3.5 Automaton for L $(r \overset{*}{1})$ $(r \overset{*}{1})$ .

EXAMPLE 3.7

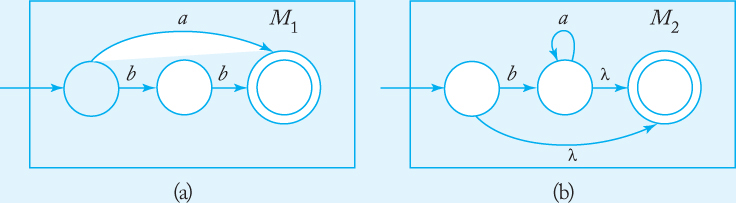
Find an nfa that accepts L (r), where

r = (a + bb)* (ba* + λ).

Automata for (a + bb) and (ba* + λ), constructed directly from first principles, are given in Figure 3.6. Putting these together using the construction in Theorem 3.1, we get the solution in Figure 3.7.

FIGURE 3.6 (a) M₁ accepts L (a + bb). (b) M₂ accepts L (ba^∗ + λ).

FIGURE 3.7 Automaton accepts L ((a + bb)^∗ (ba^∗ + λ)).

Regular Expressions for Regular Languages

It is intuitively reasonable that the converse of Theorem 3.1 should hold, and that for every regular language, there should exist a corresponding regular expression. Since any regular language has an associated nfa and hence a transition graph, all we need to do is to find a regular expression capable of generating the labels of all the walks from q₀ to any final state. This does not look too difficult but it is complicated by the existence of cycles that can often be traversed arbitrarily, in any order. This creates a bookkeeping problem that must be handled carefully. There are several ways to do this; one of the more intuitive approaches requires a side trip into what are called generalized transition graphs (GTG). Since this idea is used here in a limited way and plays no role in our further discussion, we will deal with it informally.

A generalized transition graph is a transition graph whose edges are labeled with regular expressions; otherwise it is the same as the usual transition graph. The label of any walk from the initial state to a final state is the concatenation of several regular expressions, and hence itself a regular expression. The strings denoted by such regular expressions are a subset of the language accepted by the generalized transition graph, with the full language being the union of all such generated subsets.

EXAMPLE 3.8

Figure 3.8 represents a generalized transition graph. The language accepted by it is L (a* + a* (a + b) c*), as should be clear from an inspection of the graph. The edge (q₀, q₀) labeled a is a cycle that can generate any number of a’s, that is, it represents L (a*). We could have labeled this edge a* without changing the language accepted by the graph.

FIGURE 3.8

The graph of any nondeterministic finite accepter can be considered a generalized transition graph if the edge labels are interpreted properly. An edge labeled with a single symbol a is interpreted as an edge labeled with the expression a, while an edge labeled with multiple symbols a, b, ... is interpreted as an edge labeled with the expression a + b + .... From this observation, it follows that for every regular language, there exists a generalized transition graph that accepts it. Conversely, every language accepted by a generalized transition graph is regular. Since the label of every walk in a generalized transition graph is a regular expression, this appears to be an immediate consequence of Theorem 3.1. However, there are some subtleties in the argument; we will not pursue them here, but refer the reader instead to Exercise 22, Section 4.3, for details.

Equivalence for generalized transition graphs is defined in terms of the language accepted and the purpose of the next bit of discussion is to produce a sequence of increasingly simple GTGs. In this, we will find it convenient to work with complete GTGs. A complete GTG is a graph in which all edges are present. If a GTG, after conversion from an nfa, has some edges missing, we put them in and label them with ∅. A complete GTG with |V | vertices has exactly |V |² edges.

EXAMPLE 3.9

The GTG in Figure 3.9(a) is not complete. Figure 3.9(b) shows how it is completed.

FIGURE 3.9

Suppose now that we have the simple two-state complete GTG shown in Figure 3.10. By mentally tracing through this GTG you can convince yourself that the regular expression

$r = r_{1}^{*} r_{2} {(r_{4} + r_{3} r_{1}^{*} r_{2})}^{*}$ $r = r_{1}^{*} r_{2} {(r_{4} + r_{3} r_{1}^{*} r_{2})}^{*}$

(3.1)

covers all possible paths and so is the correct regular expression associated with the graph.

When a GTG has more than two states, we can find an equivalent graph by removing one state at a time. We will illustrate this with an example before going to the general method.

FIGURE 3.10

EXAMPLE 3.10

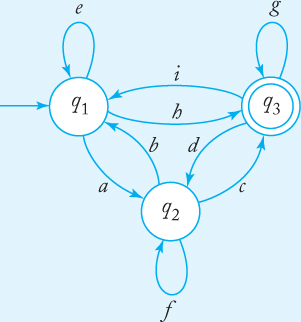
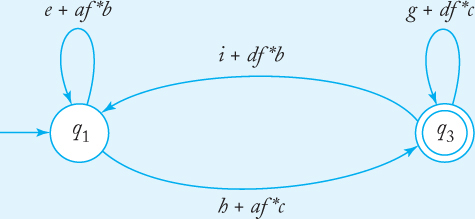
Consider the complete GTG in Figure 3.11. To remove q₂, we first introduce some new edges. We

create an edge from q₁ to q₁ and label it e + af*b,

create an edge from q₁ to q₃ and label it h + af*c,

create an edge from q₃ to q₁ and label it i + df*b,

create an edge from q₃ to q₃ and label it g + df*c.

When this is done, we remove q₂ and all associated edges. This gives the GTG in Figure 3.12. You can explore the equivalence of the two GTGs by seeing how regular expressions such as af*c and e*ab are generated.

FIGURE 3.11

FIGURE 3.12

For arbitrary GTGs we remove one state at a time until only two states are left. Then we apply Equation (3.1) to get the final regular expression. This tends to be a lengthy process, but it is straightforward as the following procedure shows.

procedure: nfa-to-rex

1. Start with an nfa with states q₀, q₁, ..., q_n, and a single final state, distinct from its initial state.

2. Convert the nfa into a complete generalized transition graph. Let r_ij stand for the label of the edge from q_i to q_j.

3. If the GTG has only two states, with q_i as its initial state and q_j its final state, its associated regular expression is

$r = r_{i i}^{*} r_{i j} {(r_{j j} + r_{j i} r_{i i}^{*} r_{i j})}^{*}$ $r = r_{i i}^{*} r_{i j} {(r_{j j} + r_{j i} r_{i i}^{*} r_{i j})}^{*}$ .

(3.2)

4. If the GTG has three states, with initial state q_i, final state q_j, and third state q_k, introduce new edges, labeled

$r_{p q} + r_{p k} r_{k k}^{*} r_{k q}$ $r_{p q} + r_{p k} r_{k k}^{*} r_{k q}$

(3.3)

for p = i, j, q = i, j. When this is done, remove vertex q_k and its associated edges.

5. If the GTG has four or more states, pick a state q_k to be removed. Apply rule 4 for all pairs of states (q_i, q_j), i ≠ k, j ≠ k. At each step apply the simplifying rules

r + ∅ = r,

r∅ = ∅,

∅* = λ,

wherever possible. When this is done, remove state q_k.

6. Repeat Steps 3 to 5 until the correct regular expression is obtained.

EXAMPLE 3.11

Find a regular expression for the language

L = {w ∈ {a, b}* : n_a (w) is even and n_b (w) is odd}.

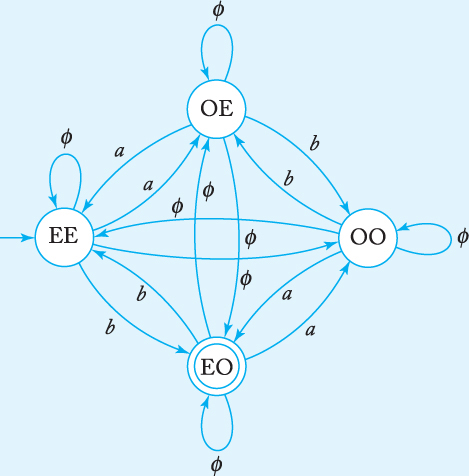
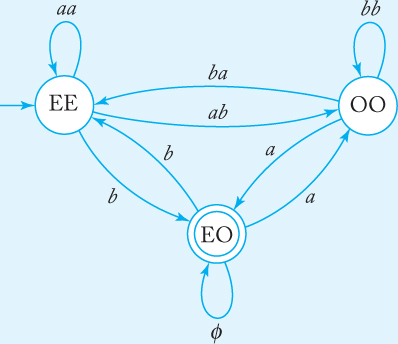
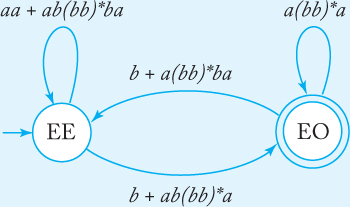
An attempt to construct a regular expression directly from this description leads to all kinds of difficulties. On the other hand, finding an nfa for it is easy as long as we use vertex labeling effectively. We label the vertices with EE to denote an even number of a’s and b’s, with OE to denote an odd number of a’s and an even number of b’s, and so on. With this we easily get the solution that, after conversion into a complete generalized transition graph, is in Figure 3.13.

We now apply the conversion to a regular expression, using procedure nfa-to-rex. To remove the state OE, we apply Equation (3.3). The edge between EE and itself will have the label

r_EE	=	∅ + a∅*a
	=	aa.

FIGURE 3.13

FIGURE 3.14

FIGURE 3.15

We continue in this manner until we get the GTG in Figure 3.14. Next, the state OO is removed, which gives Figure 3.15. Finally, we get the correct regular expression from Equation (3.2).

The process of converting an nfa to a regular expression is mechanical but tedious. It leads to regular expressions that are complicated and of little practical use. The main reason for presenting this process is that it gives the idea for the proof of an important result.

THEOREM 3.2

Let L be a regular language. Then there exists a regular expression r such that L = L(r).

Proof: If L is regular, there exists an nfa for it. We can assume without loss of generality that this nfa has a single final state, distinct from its initial state. We convert this nfa to a complete generalized transition graph and apply the procedure nfa-to-rex to it. This yields the required regular expression r.

While this can make the result plausible, a rigorous proof requires that we show that each step in the process generates an equivalent GTG. This is a technical matter we leave to the reader.

Regular Expressions for Describing Simple Patterns

In Example 1.15 and in Exercise 16, Section 2.1, we explored the connection between finite accepters and some of the simpler constituents of programming languages, such as identifiers, or integers and real numbers. The relation between finite automata and regular expressions means that we can also use regular expressions as a way of describing these features. This is easy to see; for example, in many programming languages the set of integer constants is defined by the regular expression

sdd*,

where s stands for the sign, with possible values from {+, −, λ}, and d stands for the digits 0 to 9. Integer constants are a simple case of what is sometimes called a “pattern,” a term that refers to a set of objects having some common properties. Pattern matching refers to assigning a given object to one of several categories. Often, the key to successful pattern matching is finding an effective way to describe the patterns. This is a complicated and extensive area of computer science to which we can only briefly allude. The following example is a simplified, but nevertheless instructive, demonstration of how the ideas we have talked about so far have been found useful in pattern matching.

EXAMPLE 3.12

An application of pattern matching occurs in text editing. All text editors allow files to be scanned for the occurrence of a given string; most editors extend this to permit searching for patterns. For example, the vi editor in the UNIX operating system recognizes the command /aba*c/ as an instruction to search the file for the first occurrence of the string ab, followed by an arbitrary number of a’s, followed by a c. We see from this example the need for pattern-matching editors to work with regular expressions.

A challenging task in such an application is to write an efficient program for recognizing string patterns. Searching a file for occurrences of a given string is a very simple programming exercise, but here the situation is more complicated. We have to deal with an unlimited number of arbitrarily complicated patterns; furthermore, the patterns are not fixed beforehand, but created at run time. The pattern description is part of the input, so the recognition process must be flexible. To solve this problem, ideas from automata theory are often used.

If the pattern is specified by a regular expression, the pattern-recognition program can take this description and convert it into an equivalent nfa using the construction in Theorem 3.1. Theorem 2.2 may then be used to reduce this to a dfa. This dfa, in the form of a transition table, is effectively the pattern-matching algorithm. All the programmer has to do is to provide a driver that gives the general framework for using the table. In this way we can automatically handle a large number of patterns that are defined at run time.

The efficiency of the program must also be considered. The construction of finite automata from regular expressions using Theorems 2.1 and 3.1 tends to yield automata with many states. If memory space is a problem, the state reduction method described in Section 2.4 is helpful.

EXERCISES

1. Use the construction in Theorem 3.1 to find an nfa that accepts the language L (a^∗a + ab).

2. Use the construction in Theorem 3.1 to find an nfa that accepts the language L ((aab)^∗ab).

3. Use the construction in Theorem 3.1 to find an nfa that accepts the language L (ab^∗aa + bba^∗ab).

4. Find an nfa that accepts the complement of the language in Exercise 3.

5. Give an nfa that accepts the language L ((a + b)^∗ b (a + bb)^∗).

6. Find dfa’s that accept the following languages:

(a) L (aa^∗ + aba^∗b^∗).

(b) L (ab (a + ab)^∗ (a + aa)).

(d) L (((aa^∗)^∗ b)^∗).

(e) L((aa^∗)^∗ + abb).

7. Find dfa’s that accept the following languages:

(a) L = L (ab^∗a^∗) ∪ L ((ab)^∗ ba).

(b) L = L (ab^∗a^∗) ∩ L ((b)^∗ ab).

8. Find the minimal dfa that accepts L(abb)^∗ ∪ L(a^∗bb^∗).

9. Find the minimal dfa that accepts L(a^∗bb) ∪ L(ab^∗ba).

10. Consider the following generalized transition graph.

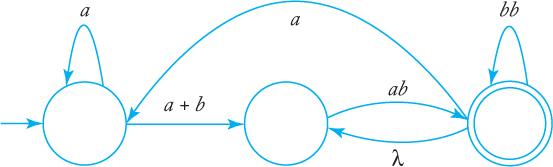
(a) Find an equivalent generalized transition graph with only two states.

(b) What is the language accepted by this graph?

11. What language is accepted by the following generalized transition graph?

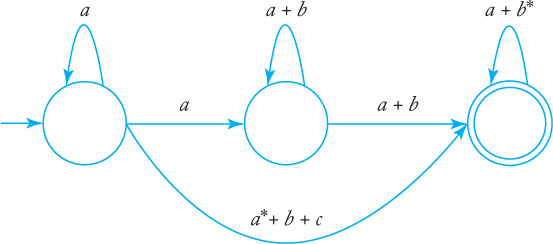
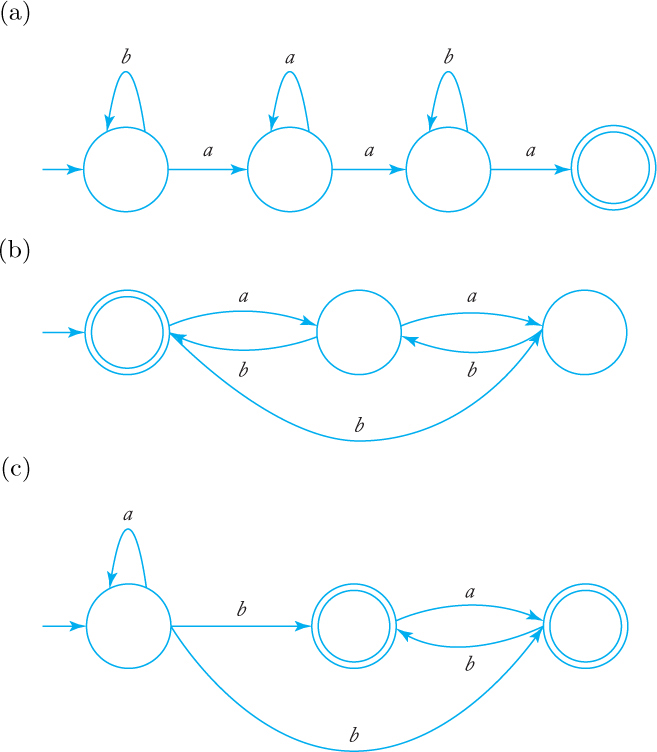
12. Find regular expressions for the languages accepted by the following automata.

13. Rework Example 3.11, this time eliminating the state OO first.

14. Show how all the labels in Figure 3.14 were obtained.

15. Find a regular expression for the following languages on {a, b}.

(a) L = {w : n_a (w) and n_b (w) are both odd}.

(b) L = {w : (n_a (w) − n_b (w)) mod 3 = 2}.

(d) L = {w : 2n_a (w) + 3n_b (w) is even}.

16. Prove that the construction suggested by Figures 3.11 and 3.12 generate equivalent generalized transition graphs.

17. Write a regular expression for the set of all C real numbers.

18. Use the construction in Theorem 3.1 to find nfa’s for L (a ⊘) and L (⊘^∗). Is the result consistent with the definition of these languages?

3.3 REGULAR GRAMMARS

A third way of describing regular languages is by means of certain grammars. Grammars are often an alternative way of specifying languages. Whenever we define a language family through an automaton or in some other way, we are interested in knowing what kind of grammar we can associate with the family. First, we look at grammars that generate regular languages.

Right- and Left-Linear Grammars

DEFINITION 3.3

A grammar G = (V, T, S, P) is said to be right-linear if all productions are of the form

A → xB,

A → x,

where A, B ∈ V, and x ∈ T*. A grammar is said to be left-linear if all productions are of the form

A → Bx,

A → x.

A regular grammar is one that is either right-linear or left-linear.

Note that in a regular grammar, at most one variable appears on the right side of any production. Furthermore, that variable must consistently be either the rightmost or leftmost symbol of the right side of any production.

EXAMPLE 3.13

The grammar G₁ = ({S}, {a, b}, S, P₁), with P₁ given as

S → abS|a

is right-linear. The grammar G₂ = ({S, S₁, S₂}, {a, b}, S, P₂), with productions

S → S₁ab,

S₁ → S₁ab|S₂,

S₂ → a,

is left-linear. Both G₁ and G₂ are regular grammars.

The sequence

S ⇒ abS ⇒ ababS ⇒ ababa

is a derivation with G₁. From this single instance it is easy to conjecture that L (G₁) is the language denoted by the regular expression r = (ab)* a. In a similar way, we can see that L (G₂) is the regular language L (aab (ab)*).

EXAMPLE 3.14

The grammar G = ({S, A, B}, {a, b}, S, P) with productions

S → A,

A → aB|λ,

B → Ab,

is not regular. Although every production is either in right-linear or left-linear form, the grammar itself is neither right-linear nor left-linear, and therefore is not regular. The grammar is an example of a linear grammar. A linear grammar is a grammar in which at most one variable can occur on the right side of any production, without restriction on the position of this variable. Clearly, a regular grammar is always linear, but not all linear grammars are regular.

Our next goal will be to show that regular grammars are associated with regular languages and that for every regular language there is a regular grammar. Thus, regular grammars are another way of talking about regular languages.

Right-Linear Grammars Generate Regular Languages

First, we show that a language generated by a right-linear grammar is always regular. To do so, we construct an nfa that mimics the derivations of a right-linear grammar. Note that the sentential forms of a right-linear grammar have the special form in which there is exactly one variable and it occurs as the rightmost symbol. Suppose now that we have a step in a derivation

ab ··· cD ⇒ ab ··· cdE,

arrived at by using a production D → dE. The corresponding nfa can imitate this step by going from state D to state E when a symbol d is encountered. In this scheme, the state of the automaton corresponds to the variable in the sentential form, while the part of the string already processed is identical to the terminal prefix of the sentential form. This simple idea is the basis for the following theorem.

THEOREM 3.3

Let G = (V, T, S, P) be a right-linear grammar. Then L (G) is a regular language.

Proof: We assume that V = {V₀, V₁, ...}, that S = V₀, and that we have productions of the form V₀ → v₁V_i, V_i → v₂V_j, ... or V_n → v_l, .... If w is a string in L (G), then because of the form of the productions

$\begin{matrix} V_{0} & \Rightarrow & υ_{1} V_{i} \\ \Rightarrow & υ_{1} υ_{2} V_{j} \\ \overset{*}{\begin{matrix} \Rightarrow \end{matrix}} & υ_{1} υ_{2} \dots υ_{k} V_{n} \\ \Rightarrow & υ_{1} υ_{2} \dots υ_{k} υ_{l} = w . \end{matrix}$ $\begin{matrix} V_{0} & \Rightarrow & υ_{1} V_{i} \\ \Rightarrow & υ_{1} υ_{2} V_{j} \\ \overset{*}{\begin{matrix} \Rightarrow \end{matrix}} & υ_{1} υ_{2} \dots υ_{k} V_{n} \\ \Rightarrow & υ_{1} υ_{2} \dots υ_{k} υ_{l} = w . \end{matrix}$

(3.4)

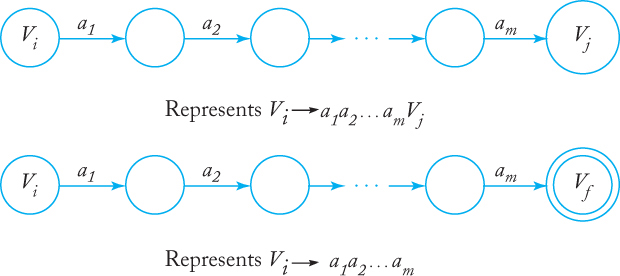
The automaton to be constructed will reproduce the derivation by consuming each of these v’s in turn. The initial state of the automaton will be labeled V₀, and for each variable V_i there will be a nonfinal state labeled V_i. For each production

V_i → a₁a₂ ··· a_mV_j,

the automaton will have transitions to connect V_i and V_j that is, δ will be defined so that

δ* (V_i, a₁a₂ ··· a_m) = V_j.

For each production

V_i → a₁a₂ ··· a_m,

the corresponding transition of the automaton will be

δ* (V_i, a₁a₂ ··· a_m) = V_f,

where V_f is a final state. The intermediate states that are needed to do this are of no concern and can be given arbitrary labels. The general scheme is shown in Figure 3.16. The complete automaton is assembled from such individual parts.

FIGURE 3.16

Suppose now that w ∈ L (G) so that (3.4) is satisfied. In the nfa there is, by construction, a path from V₀ to V_i labeled v₁, a path from V_i to V_j labeled v₂, and so on, so that clearly

V_f ∈ δ* (V₀, w),

and w is accepted by M.

Conversely, assume that w is accepted by M. Because of the way in which M was constructed, to accept w the automaton has to pass through a sequence of states V₀, V_i, ... to V_f, using paths labeled v₁, v₂, .... Therefore, w must have the form

w = v₁v₂ ··· v_kv_l

and the derivation

$V_{o} \Rightarrow υ_{1} V_{i} \Rightarrow υ_{1} υ_{2} V_{j} \overset{*}{\Rightarrow} υ_{1} υ_{2} \dots υ_{k} V_{k} \Rightarrow υ_{1} υ_{2} \dots υ_{k} υ_{1}$ $V_{o} \Rightarrow υ_{1} V_{i} \Rightarrow υ_{1} υ_{2} V_{j} \overset{*}{\Rightarrow} υ_{1} υ_{2} \dots υ_{k} V_{k} \Rightarrow υ_{1} υ_{2} \dots υ_{k} υ_{1}$

is possible. Hence w is in L (G), and the theorem is proved.

EXAMPLE 3.15

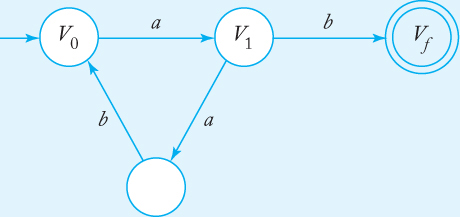
Construct a finite automaton that accepts the language generated by the grammar

V₀ → aV₁,

V₁ → abV₀|b,

where V₀ is the start variable. We start the transition graph with vertices V₀, V₁, and V_f. The first production rule creates an edge labeled a between V₀ and V₁. For the second rule, we need to introduce an additional vertex so that there is a path labeled ab between V₁ and V₀. Finally, we need to add an edge labeled b between V₁ and V_f, giving the automaton shown in Figure 3.17. The language generated by the grammar and accepted by the automaton is the regular language L ((aab)* ab).

FIGURE 3.17

Right-Linear Grammars for Regular Languages

To show that every regular language can be generated by some right-linear grammar, we start from the dfa for the language and reverse the construction shown in Theorem 3.3. The states of the dfa now become the variables of the grammar, and the symbols causing the transitions become the terminals in the productions.

THEOREM 3.4

If L is a regular language on the alphabet Σ, then there exists a right-linear grammar G = (V, Σ, S, P) such that L = L (G).

Proof: Let M = (Q, Σ, δ, q₀, F) be a dfa that accepts L. We assume that Q = {q₀, q₁, ..., q_n} and Σ = {a₁, a₂, ..., a_m}. Construct the right-linear grammar G = (V, Σ, S, P) with

V = {q₀, q₁, ..., q_n}

and S = q₀. For each transition

δ (q_i, a_j) = q_k

of M, we put in P the production

q_i → a_jq_k.

(3.5)

In addition, if q_k is in F, we add to P the production

q_k → λ.

(3.6)

We first show that G defined in this way can generate every string in L. Consider w ∈ L of the form

w = a_ia_j ··· a_ka_l.

For M to accept this string it must make moves via

δ (q₀, a_i)	=	q_p,
δ (q_p, a_j)	=	q_r,
	⋮
δ (q_s, a_k)	=	q_t,
δ (q_t, a_l)	=	q_f ∈ F.

By construction, the grammar will have one production for each of these δ’s. Therefore, we can make the derivation

$\begin{matrix} q_{0} & \Rightarrow & a_{i} q_{p} \Rightarrow a_{i} a_{j} q_{r} \overset{*}{\Rightarrow} a_{i} a_{j} \dots a_{k} q_{t} \\ \Rightarrow & a_{i} a_{j} \dots a_{k} a_{l} q_{f} \Rightarrow a_{i} a_{j} \dots a_{k} a_{l}, \end{matrix}$ $\begin{matrix} q_{0} & \Rightarrow & a_{i} q_{p} \Rightarrow a_{i} a_{j} q_{r} \overset{*}{\Rightarrow} a_{i} a_{j} \dots a_{k} q_{t} \\ \Rightarrow & a_{i} a_{j} \dots a_{k} a_{l} q_{f} \Rightarrow a_{i} a_{j} \dots a_{k} a_{l}, \end{matrix}$

(3.7)

with the grammar G, and w ∈ L (G).

Conversely, if w ∈ L (G), then its derivation must have the form (3.7). But this implies that

δ* (q₀, a_ia_j ··· a_ka_l) = q_f,

completing the proof.

For the purpose of constructing a grammar, it is useful to note that the restriction that M be a dfa is not essential to the proof of Theorem 3.4. With minor modification, the same construction can be used if M is an nfa.

EXAMPLE 3.16

Construct a right-linear grammar for L (aab*a). The transition function for an nfa, together with the corresponding grammar productions, is given in Figure 3.18. The result was obtained by simply following the construction in Theorem 3.4. The string aaba can be derived with the constructed grammar by

q₀ ⇒ aq₁ ⇒ aaq₂ ⇒ aabq₂ ⇒ aabaq_f ⇒ aaba.

FIGURE 3.18

Equivalence of Regular Languages and Regular Grammars

The previous two theorems establish the connection between regular languages and right-linear grammars. One can make a similar connection between regular languages and left-linear grammars, thereby showing the complete equivalence of regular grammars and regular languages.

THEOREM 3.5

A language L is regular if and only if there exists a left-linear grammar G such that L = L (G).

Proof: We only outline the main idea. Given any left-linear grammar with productions of the form

A → Bv,

A → v,

we construct from it a right-linear grammar $\hat{G}$ $\hat{G}$ by replacing every such production of G with

A → v^RB,

A → v^R,

respectively. A few examples will make it clear quickly that $L (G) = {(L (\hat{G}))}^{R}$ $L (G) = {(L (\hat{G}))}^{R}$ . Next, we use Exercise 12, Section 2.3, which tells us that the reverse of any regular language is also regular. Since $\hat{G}$ $\hat{G}$ is right-linear, $L (\hat{G})$ $L (\hat{G})$ is regular. But then so are ${L ((\hat{G}))}^{R}$ ${L ((\hat{G}))}^{R}$ and L (G).

Putting Theorems 3.4 and 3.5 together, we arrive at the equivalence of regular languages and regular grammars.

THEOREM 3.6

A language L is regular if and only if there exists a regular grammar G such that L = L (G).

We now have several ways of describing regular languages: dfa’s, nfa’s, regular expressions, and regular grammars. While in some instances one or the other of these may be most suitable, they are all equally powerful.

FIGURE 3.19

Each gives a complete and unambiguous definition of a regular language. The connection between all these concepts is established by the four theorems in this chapter, as shown in Figure 3.19.

EXERCISES

1. Construct a dfa that accepts the language generated by the grammar

S → abA,

A → baB,

B → aA|bb.

2. Construct a dfa that accepts the language generated by the grammar

S → abS|A,

A → baB,

B → aA|bb.

3. Find a regular grammar that generates the language L (aa^∗ (ab + a)^∗).

4. Construct a left-linear grammar for the language in Exercise 1.

5. Construct right- and left-linear grammars for the language

L = {aⁿb^m : n ≥ 3, m ≥ 2}.

6. Construct a right-linear grammar for the language L ((aaab^∗ab)^∗).

7. Find a regular grammar that generates the language on Σ = {a, b} consisting of all strings with no more than two a’s.

8. In Theorem 3.5, prove that $L (\hat{G}) = {(L (G))}^{R}$ $L (\hat{G}) = {(L (G))}^{R}$ .

9. Suggest a construction by which a left-linear grammar can be obtained from an nfa directly.

10. Use the construction suggested by the above exercises to construct a left-linear grammar for the nfa below.

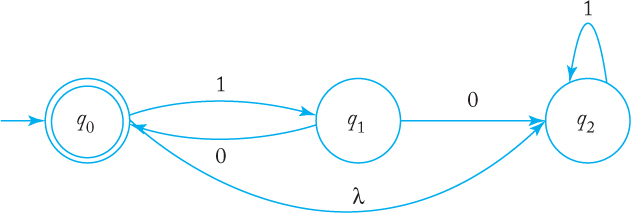
11. Find a left-linear grammar for the language L ((aaab^∗ba)^∗).

12. Find a regular grammar for the language L = {aⁿb^m : n + m is odd}.

13. Find a regular grammar that generates the language

L = {w ∈ {a, b}^∗ : n_a (w) + 3n_b (w) is odd}.

14. Find regular grammars for the following languages on {a, b}:

(a) L = {w : n_a(w) is even, n_b(w) ≥ 4}.

(b) L = {w : n_a (w) and n_b (w) are both even}.)

(d) L = {w : (n_a (w) − n_b (w)) mod 3 ≠ 1}.

(e) L = {w : (n_a (w) − n_b (w)) mod 3 ≠ 0}.

(f) L = {w : |n_a (w) − n_b (w)| is odd}.

15. Show that for every regular language not containing λ there exists a right-linear grammar whose productions are restricted to the forms

A → aB,

A → a,

where A, B ∈ V, and a ∈ T.

16. Show that any regular grammar G for which L (G) ⊘= ⊘ must have at least one production of the form

A → x

where A ∈ V and x ∈ T ^∗.

17. Find a regular grammar that generates the set of all real numbers in C.

18. Let G₁ = (V₁, Σ, S₁, P₁) be right-linear and G₂ = (V₂, Σ, S₂, P₂) be a left-linear grammar, and assume that V₁ and V₂ are disjoint. Consider the linear grammar G = ({S} ∪ V₁ ∪ V₂, Σ, S, P), where S is not in V₁ ∪ V₂ and P = {S → S₁|S₂} ∪ P₁ ∪ P₂. Show that L (G) is regular.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Chapter 3: Regular Languages and Regular Grammars

Create new playlist

Sign In

Sign Up

CHAPTER 3

CHAPTER SUMMARY

3.1 REGULAR EXPRESSIONS

Formal Definition of a Regular Expression

Languages Associated with Regular Expressions

EXERCISES

3.2 CONNECTION BETWEEN REGULAR EXPRESSIONS AND REGULAR LANGUAGES

Regular Expressions Denote Regular Languages

Regular Expressions for Regular Languages

Regular Expressions for Describing Simple Patterns

EXERCISES

3.3 REGULAR GRAMMARS

Right- and Left-Linear Grammars

Right-Linear Grammars Generate Regular Languages

Right-Linear Grammars for Regular Languages

Equivalence of Regular Languages and Regular Grammars

EXERCISES

Table of Contents for
Chapter 3: Regular Languages and Regular Grammars